Representación matricial de secciones cónicas

En matemáticas , la representación matricial de las secciones cónicas permite utilizar las herramientas del álgebra lineal en el estudio de las secciones cónicas . Proporciona formas sencillas de calcular el eje , los vértices , las tangentes y la relación polar y de polos entre puntos y líneas del plano determinado por la cónica. La técnica no requiere poner la ecuación de una sección cónica en una forma estándar, lo que facilita la investigación de aquellas secciones cónicas cuyos ejes no son paralelos al sistema de coordenadas .

Las secciones cónicas (incluidas las degeneradas ) son los conjuntos de puntos cuyas coordenadas satisfacen una ecuación polinómica de segundo grado en dos variables, Por un abuso de notación , también se llamará sección cónica a esta cuando no pueda surgir confusión. $${\displaystyle Q(x,y)=Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0.}$$ ${\displaystyle Q}$

Esta ecuación se puede escribir en notación matricial , en términos de una matriz simétrica para simplificar algunas fórmulas posteriores, como ^[1]

$${\displaystyle {\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}D&E\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+F=0.}$$

La suma de los tres primeros términos de esta ecuación, es decir, es la forma cuadrática asociada a la ecuación y la matriz se denomina matriz de la forma cuadrática . La traza y el determinante de son ambos invariantes con respecto a la rotación de los ejes y la traslación del plano (movimiento del origen). ^{[2] [3]} $${\displaystyle Ax^{2}+Bxy+Cy^{2}={\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}},}$$ $${\displaystyle A_{33}={\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}}$$ ${\displaystyle A_{33}}$

La ecuación cuadrática también se puede escribir como

$${\displaystyle \mathbf {x} ^{\mathsf {T}}A_{Q}\mathbf {x} =0,}$$

donde es el vector de coordenadas homogéneo en tres variables restringido de manera que la última variable sea 1, es decir, ${\displaystyle \mathbf {x} }$

$${\displaystyle {\begin{pmatrix}x\\y\\1\end{pmatrix}}}$$

y donde esta la matriz ${\displaystyle A_{Q}}$

$${\displaystyle A_{Q}={\begin{pmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{pmatrix}}.}$$La matriz se denomina matriz de la ecuación cuadrática . ^[4] Al igual que la de , su determinante es invariante con respecto tanto a la rotación como a la traslación. ^[3] ${\displaystyle A_{Q}}$ ${\displaystyle A_{33}}$

La submatriz superior izquierda de 2 × 2 (una matriz de orden 2) de , obtenida al eliminar la tercera (última) fila y la tercera (última) columna de es la matriz de la forma cuadrática. La notación anterior se utiliza en este artículo para enfatizar esta relación. ${\displaystyle A_{Q}}$ ${\displaystyle A_{Q}}$ ${\displaystyle A_{33}}$

Clasificación

Las secciones cónicas propias (no degeneradas) y degeneradas se pueden distinguir ^{[5] [6]} basándose en el determinante de : ${\displaystyle A_{Q}=(AC-{\frac {B^{2}}{4}})F+{\frac {BDE-C{D}^{2}-A{E}^{2}}{4}}}$

Si , la cónica es degenerada. ${\displaystyle \det A_{Q}=0}$

Si es así, no es degenerada, podemos ver qué tipo de sección cónica es calculando el menor , : ${\displaystyle \det A_{Q}\neq 0}$ ${\displaystyle Q}$ ${\displaystyle \det A_{33}=AC-{\frac {B^{2}}{4}}}$

• ${\displaystyle Q}$es una hipérbola si y sólo si , ${\displaystyle \det A_{33}<0}$
• ${\displaystyle Q}$es una parábola si y sólo si , y ${\displaystyle \det A_{33}=0}$
• ${\displaystyle Q}$es una elipse si y sólo si . ${\displaystyle \det A_{33}>0}$

En el caso de una elipse, podemos distinguir el caso especial de un círculo comparando los dos últimos elementos diagonales correspondientes a los coeficientes de , y : ${\displaystyle x^{2}}$ ${\displaystyle xy}$ ${\displaystyle y^{2}}$

• Si y , entonces es un círculo. ${\displaystyle A=C}$ ${\displaystyle B=0}$ ${\displaystyle Q}$

Además, en el caso de una elipse no degenerada (con y ), tenemos una elipse real si pero una elipse imaginaria si . Un ejemplo de esto último es , que no tiene soluciones de valor real. ${\displaystyle \det A_{33}>0}$ ${\displaystyle \det A_{Q}\neq 0}$ ${\displaystyle (A+C)\det A_{Q}<0}$ ${\displaystyle (A+C)\det A_{Q}>0}$ ${\displaystyle x^{2}+y^{2}+10=0}$

Si la sección cónica es degenerada ( ), aún nos permite distinguir su forma: ${\displaystyle \det A_{Q}=0}$ ${\displaystyle \det A_{33}}$

• Dos rectas que se intersectan (una hipérbola degenerada en sus dos asíntotas) si y sólo si . ${\displaystyle \det A_{33}<0}$
• Dos rectas paralelas (parábola degenerada) si y solo si . Estas rectas son distintas y reales si , coincidentes si , e inexistentes en el plano real si . ${\displaystyle \det A_{33}=0}$ ${\displaystyle D^{2}+E^{2}>4(A+C)F}$ ${\displaystyle D^{2}+E^{2}=4(A+C)F}$ ${\displaystyle D^{2}+E^{2}<4(A+C)F}$
• Un solo punto (una elipse degenerada) si y sólo si . ${\displaystyle \det A_{33}>0}$

El caso de líneas coincidentes ocurre si y sólo si el rango de la matriz 3 × 3 es 1; en todos los demás casos degenerados su rango es 2. ^[2] ${\displaystyle A_{Q}}$

Cónicas centrales

Cuando existe un centro geométrico de la sección cónica y dichas secciones cónicas (elipses e hipérbolas) se denominan cónicas centrales . ^[7] ${\displaystyle \det A_{33}\neq 0}$

Centro

El centro de una cónica, si existe, es un punto que biseca todas las cuerdas de la cónica que pasan por él. Esta propiedad se puede utilizar para calcular las coordenadas del centro, que se puede demostrar que es el punto donde el gradiente de la función cuadrática Q se anula, es decir, ^[8] Esto da como resultado el centro que se indica a continuación. $${\displaystyle \nabla Q=\left[{\frac {\partial Q}{\partial x}},{\frac {\partial Q}{\partial y}}\right]=[0,0].}$$

Un enfoque alternativo que utiliza la forma matricial de la ecuación cuadrática se basa en el hecho de que cuando el centro es el origen del sistema de coordenadas, no hay términos lineales en la ecuación. Cualquier traslación a un origen de coordenadas ( x ₀ , y ₀ ) , utilizando x * = x – x ₀ , y * = y − y ₀ da lugar a

$${\displaystyle {\begin{pmatrix}x^{*}+x_{0}&y^{*}+y_{0}\end{pmatrix}}{\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}{\begin{pmatrix}x^{*}+x_{0}\\y^{*}+y_{0}\end{pmatrix}}+\left({\begin{matrix}D&E\end{matrix}}\right)\left({\begin{matrix}x^{*}+x_{0}\\y^{*}+y_{0}\end{matrix}}\right)+F=0.}$$

La condición para que ( x ₀ , y ₀ ) sea el centro de la cónica ( x _c , y _c ) es que los coeficientes de los términos lineales x* e y* , cuando se multiplica esta ecuación, sean cero. Esta condición produce las coordenadas del centro: $${\displaystyle {\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}={\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}^{\!-1}{\begin{pmatrix}-D/2\\-E/2\end{pmatrix}}={\begin{pmatrix}(BE-2CD)/(4AC-B^{2})\\(DB-2AE)/(4AC-B^{2})\end{pmatrix}}.}$$

Este cálculo también se puede realizar tomando las dos primeras filas de la matriz asociada A _Q , multiplicando cada una por ( x , y , 1) ^⊤ y estableciendo ambos productos internos iguales a 0, obteniendo el siguiente sistema:

$${\displaystyle {\begin{aligned}Ax+(B/2)y+D/2&=0,\\(B/2)x+Cy+E/2&=0.\end{aligned}}}$$

Esto produce el punto central mencionado anteriormente.

En el caso de una parábola, es decir, cuando 4 AC − B ² = 0 , no hay centro ya que los denominadores anteriores se vuelven cero (o, interpretado proyectivamente , el centro está en la recta del infinito ).

Ecuación matricial centrada

Una cónica central (no parabólica) se puede reescribir en forma de matriz centrada como donde ${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}$ $${\displaystyle {\begin{pmatrix}x-x_{c}&y-y_{c}\end{pmatrix}}{\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}{\begin{pmatrix}x-x_{c}\\y-y_{c}\end{pmatrix}}=K,}$$ $${\displaystyle K=-{\frac {\det(A_{Q})}{AC-(B/2)^{2}}}=-{\frac {\det(A_{Q})}{\det(A_{33})}}.}$$

Entonces, para el caso de elipse de AC > ( B /2) ² , la elipse es real si el signo de K es igual al signo de ( A + C ) (es decir, el signo de cada uno de A y C ), imaginaria si tienen signos opuestos, y una elipse puntual degenerada si K = 0 . En el caso de hipérbola de AC < ( B /2) ² , la hipérbola es degenerada si y solo si K = 0 .

Forma estándar de una cónica central

La forma estándar de la ecuación de una sección cónica central se obtiene cuando la sección cónica se traslada y rota de modo que su centro se encuentre en el centro del sistema de coordenadas y sus ejes coincidan con los ejes de coordenadas. Esto es equivalente a decir que el centro del sistema de coordenadas se mueve y los ejes de coordenadas se rotan para satisfacer estas propiedades. En el diagrama, el sistema de coordenadas xy original con origen O se mueve al sistema de coordenadas x'y' con origen O' .

Traslación y rotación de coordenadas

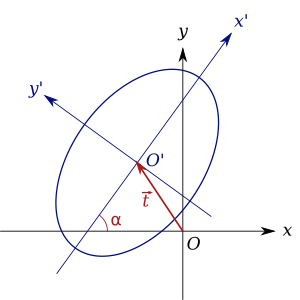
La traducción es por el vector. ${\displaystyle \mathbf {t} ={\begin{pmatrix}x_{c}\\y_{c}\end{pmatrix}}.}$

La rotación en el ángulo α se puede realizar diagonalizando la matriz A ₃₃ . Así, si y son los valores propios de la matriz A ₃₃ , la ecuación centrada se puede reescribir en las nuevas variables x' e y' como ^[9] ${\displaystyle \lambda _{1}}$ ${\displaystyle \lambda _{2}}$

$${\displaystyle \lambda _{1}x'^{2}+\lambda _{2}y'^{2}=-{\frac {\det A_{Q}}{\det A_{33}}}.}$$

Dividiendo por obtenemos una forma canónica estándar. ${\displaystyle K=-{\frac {\det A_{Q}}{\det A_{33}}}}$

Por ejemplo, para una elipse, esta forma es De aquí obtenemos a y b , las longitudes de los semiejes mayor y semieje menor en notación convencional. $${\displaystyle {\frac {{x'}^{2}}{a^{2}}}+{\frac {{y'}^{2}}{b^{2}}}=1.}$$

Para las cónicas centrales, ambos valores propios son distintos de cero y la clasificación de las secciones cónicas se puede obtener examinándolas. ^[10]

• Si λ ₁ y λ ₂ tienen el mismo signo algebraico, entonces Q es una elipse real, una elipse imaginaria o un punto real si K tiene el mismo signo, tiene el signo opuesto o es cero, respectivamente.
• Si λ ₁ y λ ₂ tienen signos algebraicos opuestos, entonces Q es una hipérbola o dos líneas que se intersecan dependiendo de si K es distinto de cero o cero, respectivamente.

Ejes

Según el teorema del eje principal , los dos vectores propios de la matriz de la forma cuadrática de una sección cónica central (elipse o hipérbola) son perpendiculares ( ortogonales entre sí) y cada uno es paralelo a (en la misma dirección que) el eje mayor o menor de la cónica. El vector propio que tiene el valor propio más pequeño (en valor absoluto ) corresponde al eje mayor. ^[11]

Específicamente, si una sección cónica central tiene centro ( x _c , y _c ) y un vector propio de A ₃₃ está dado por v ( v ₁ , v ₂ ) entonces el eje principal (mayor o menor) correspondiente a ese vector propio tiene ecuación, $${\displaystyle {\frac {x-x_{c}}{v_{1}}}={\frac {y-y_{c}}{v_{2}}}.}$$

Vértices

Los vértices de una cónica central se pueden determinar calculando las intersecciones de la cónica y sus ejes, es decir, resolviendo el sistema formado por la ecuación de la cónica cuadrática y la ecuación lineal para uno u otro de los ejes alternativamente. Se obtienen dos o ningún vértice para cada eje, ya que, en el caso de la hipérbola, el eje menor no interseca a la hipérbola en un punto con coordenadas reales. Sin embargo, desde la visión más amplia del plano complejo , el eje menor de una hipérbola sí interseca a la hipérbola, pero en puntos con coordenadas complejas. ^[12]

Polos y polares

Utilizando coordenadas homogéneas , ^[13] los puntos ^[14] y son conjugados respecto de la cónica Q proporcionada $${\displaystyle \mathbf {p} ={\begin{pmatrix}p_{0}\\p_{1}\\p_{2}\end{pmatrix}}}$$ ${\displaystyle \mathbf {r} ={\begin{pmatrix}r_{0}\\r_{1}\\r_{2}\end{pmatrix}}}$ $${\displaystyle \mathbf {p} ^{\mathsf {T}}A_{Q}\mathbf {r} =0.}$$

Los conjugados de un punto fijo p forman una línea o están formados por todos los puntos del plano de la cónica. Cuando los conjugados de p forman una línea, la línea se denomina polar de p y el punto p se denomina polo de la línea con respecto a la cónica. Esta relación entre puntos y líneas se denomina polaridad .

Si la cónica no es degenerada, los conjugados de un punto siempre forman una recta y la polaridad definida por la cónica es una biyección entre los puntos y rectas del plano extendido que contiene la cónica (es decir, el plano junto con los puntos y la recta en el infinito ).

Si el punto p se encuentra en la cónica Q , la línea polar de p es la línea tangente a Q en p .

La ecuación, en coordenadas homogéneas, de la recta polar del punto p respecto de la cónica no degenerada Q está dada por $${\displaystyle \mathbf {p} ^{T}A_{Q}{\begin{pmatrix}x\\y\\z\end{pmatrix}}=0.}$$

Así como p determina de forma única su línea polar (con respecto a una cónica dada), cada línea determina un polo único p . Además, un punto p está en una línea L que es la polar de un punto r , si y solo si la polar de p pasa por el punto r ( teorema de La Hire ). ^[15] Por lo tanto, esta relación es una expresión de dualidad geométrica entre puntos y líneas en el plano.

Varios conceptos familiares sobre las secciones cónicas están directamente relacionados con esta polaridad. El centro de una cónica no degenerada puede identificarse como el polo de la línea en el infinito. Una parábola, al ser tangente a la línea en el infinito, tendría su centro en un punto de la línea en el infinito. Las hipérbolas intersecan la línea en el infinito en dos puntos distintos y las líneas polares de estos puntos son las asíntotas de la hipérbola y son las líneas tangentes a la hipérbola en estos puntos del infinito. Además, la línea polar de un foco de la cónica es su directriz correspondiente. ^[16]

Tangentes

Sea la recta L la recta polar del punto p respecto de la cónica no degenerada Q . Por el teorema de La Hire, toda recta que pase por p tiene su polo en L . Si L interseca a Q en dos puntos (el máximo posible) entonces las polares de esos puntos son rectas tangentes que pasan por p y tal punto se llama punto exterior o externo de Q . Si L interseca a Q en un solo punto, entonces es una recta tangente y p es el punto de tangencia. Finalmente, si L no interseca a Q entonces p no tiene rectas tangentes que lo pasen y se llama punto interior o interno . ^[17]

La ecuación de la recta tangente (en coordenadas homogéneas) en un punto p de la cónica no degenerada Q está dada por,

$${\displaystyle \mathbf {p} ^{\mathsf {T}}A_{Q}{\begin{pmatrix}x\\y\\z\end{pmatrix}}=0.}$$

Si p es un punto exterior, primero hay que hallar la ecuación de su polar (la ecuación anterior) y luego las intersecciones de esa línea con la cónica, por ejemplo en los puntos s y t . Las polares de s y t serán las tangentes que pasan por p .

Utilizando la teoría de polos y polares, el problema de encontrar las cuatro tangentes mutuas de dos cónicas se reduce a encontrar la intersección de dos cónicas .

Véase también

• Sección cónica § Forma cartesiana general
• Forma cuadrática (estadística)

Notas

1. Brannan, Esplen y Gray 1999, pág. 30
2. Pettofrezzo 1978, pág. 110
3. España 2007, págs. 59–62
4. También es una matriz de forma cuadrática, pero esta forma tiene tres variables y es . ${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}}$
5. Lawrence 1972, pág. 63
6. España 2007, p. 70
7. Pettofrezzo 1978, pág. 105
8. Ayoub 1993, pág. 322
9. Ayoub 1993, pág. 324
10. Pettofrezzo 1978, pág. 108
11. Ostermann y Wanner 2012, pág. 311
12. Kendig, Keith (2005), Cónicas , Asociación Matemática de Estados Unidos, págs. 89-102, ISBN 978-0-88385-335-1
13. Esto permite la inclusión algebraica de infinitos puntos y una línea en el infinito que son necesarios para algunos de los siguientes resultados
14. Esta sección sigue a Fishback, WT (1969), Projective and Euclidean Geometry (2.ª ed.), Wiley, págs. 167-172
15. Brannan, Esplen y Gray 1999, pág. 189
16. Akopyan, AV; Zaslavsky, AA (2007), Geometría de las cónicas , American Mathematical Society, pág. 72, ISBN 978-0-8218-4323-9
17. Interpretado en el plano complejo tal punto está en dos rectas tangentes complejas que cortan Q en puntos complejos.

Referencias

• Ayoub, AB (1993), "Revisitando las secciones cónicas centrales", Mathematics Magazine , 66 (5): 322–325, doi :10.1080/0025570x.1993.11996157
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometría , Cambridge University Press, ISBN 978-0-521-59787-6
• Lawrence, J. Dennis (1972), Un catálogo de curvas planas especiales , Dover
• Ostermann, Alexander; Wanner, Gerhard (2012), La geometría según su historia , Springer, doi :10.1007/978-3-642-29163-0, ISBN 978-3-642-29163-0
• Pettofrezzo, Anthony (1978) [1966], Matrices y transformaciones , Dover, ISBN 978-0-486-63634-4
• España, Barry (2007) [1957], Cónicas analíticas , Dover, ISBN 978-0-486-45773-4