La magnetorresistencia gigante ( GMR ) es un efecto de magnetorresistencia mecánico cuántico observado en multicapas compuestas por capas conductoras ferromagnéticas y no magnéticas alternadas. El Premio Nobel de Física de 2007 fue otorgado a Albert Fert y Peter Grünberg por el descubrimiento de la GMR, que también sienta las bases para el estudio de la espintrónica .
El efecto se observa como un cambio significativo en la resistencia eléctrica dependiendo de si la magnetización de las capas ferromagnéticas adyacentes está en una alineación paralela o antiparalela . La resistencia total es relativamente baja para la alineación paralela y relativamente alta para la alineación antiparalela. La dirección de magnetización se puede controlar, por ejemplo, aplicando un campo magnético externo. El efecto se basa en la dependencia de la dispersión de electrones con la orientación del espín.
La principal aplicación de GMR es en sensores de campo magnético , que se utilizan para leer datos en unidades de disco duro , biosensores , sistemas microelectromecánicos (MEMS) y otros dispositivos. [1] Las estructuras multicapa GMR también se utilizan en la memoria de acceso aleatorio magnetorresistiva (MRAM) como celdas que almacenan un bit de información.
En la literatura, el término magnetorresistencia gigante a veces se confunde con la magnetorresistencia colosal de los semiconductores ferromagnéticos y antiferromagnéticos , que no está relacionada con una estructura multicapa. [2] [3]

La magnetorresistencia es la dependencia de la resistencia eléctrica de una muestra con respecto a la intensidad de un campo magnético externo. Numéricamente, se caracteriza por el valor
donde R(H) es la resistencia de la muestra en un campo magnético H, y R(0) corresponde a H = 0. [4] Las formas alternativas de esta expresión pueden usar resistividad eléctrica en lugar de resistencia, un signo diferente para δ H , [5] y a veces se normalizan por R(H) en lugar de R(0). [6]
El término "magnetorresistencia gigante" indica que el valor δ H para estructuras multicapa supera significativamente la magnetorresistencia anisotrópica, que tiene un valor típico dentro de unos pocos porcentajes. [7] [8]
La GMR fue descubierta en 1988 de forma independiente [9] [10] por los grupos de Albert Fert de la Universidad de París-Sur , Francia, y Peter Grünberg del Forschungszentrum Jülich , Alemania. La importancia práctica de este descubrimiento experimental fue reconocida con el Premio Nobel de Física otorgado a Fert y Grünberg en 2007. [11]
El primer modelo matemático que describe el efecto de la magnetización sobre la movilidad de los portadores de carga en sólidos , relacionado con el espín de esos portadores, se informó en 1936. La evidencia experimental de la mejora potencial de δ H se conoce desde la década de 1960. A fines de la década de 1980, la magnetorresistencia anisotrópica había sido bien explorada, [12] [13] pero el valor correspondiente de δ H no excedió un pequeño porcentaje. [7] La mejora de δ H se hizo posible con el advenimiento de técnicas de preparación de muestras como la epitaxia de haz molecular , que permite fabricar películas delgadas multicapa con un espesor de varios nanómetros. [14]
Fert y Grünberg estudiaron la resistencia eléctrica de estructuras que incorporaban materiales ferromagnéticos y no ferromagnéticos. En particular, Fert trabajó en películas multicapa y Grünberg descubrió en 1986 la interacción de intercambio antiferromagnético en películas Fe/Cr. [14]
El trabajo de descubrimiento de GMR fue llevado a cabo por los dos grupos en muestras ligeramente diferentes. El grupo Fert utilizó superredes de (001)Fe/(001)Cr en las que las capas de Fe y Cr se depositaron en un alto vacío sobre un sustrato de (001)GaAs mantenido a 20 °C y las mediciones de magnetorresistencia se tomaron a baja temperatura (normalmente 4,2 K). [10] El trabajo de Grünberg se realizó en multicapas de Fe y Cr sobre (110)GaAs a temperatura ambiente. [9]
En multicapas de Fe/Cr con capas de hierro de 3 nm de espesor, aumentar el espesor de las capas no magnéticas de Cr de 0,9 a 3 nm debilitó el acoplamiento antiferromagnético entre las capas de Fe y redujo el campo de desmagnetización, que también disminuyó cuando la muestra se calentó de 4,2 K a temperatura ambiente. Cambiar el espesor de las capas no magnéticas condujo a una reducción significativa de la magnetización residual en el bucle de histéresis. La resistencia eléctrica cambió hasta en un 50% con el campo magnético externo a 4,2 K. Fert denominó al nuevo efecto magnetorresistencia gigante, para resaltar su diferencia con la magnetorresistencia anisotrópica. [10] [15] El experimento de Grünberg [9] hizo el mismo descubrimiento, pero el efecto fue menos pronunciado (3% en comparación con el 50%) debido a que las muestras estaban a temperatura ambiente en lugar de a baja temperatura.
Los descubridores sugirieron que el efecto se basa en la dispersión de electrones dependiente del espín en la superred, particularmente en la dependencia de la resistencia de las capas en las orientaciones relativas de la magnetización y los espines de los electrones. [9] [10] La teoría de GMR para diferentes direcciones de la corriente se desarrolló en los siguientes años. En 1989, Camley y Barnaś calcularon la geometría de "corriente en el plano" (CIP), donde la corriente fluye a lo largo de las capas, en la aproximación clásica, [16] mientras que Levy et al. utilizaron el formalismo cuántico. [17] La teoría de la GMR para la corriente perpendicular a las capas (corriente perpendicular al plano o geometría CPP), conocida como la teoría de Valet-Fert, fue reportada en 1993. [18] Las aplicaciones favorecen la geometría CPP [19] porque proporciona una mayor relación de magnetorresistencia (δ H ), [20] lo que resulta en una mayor sensibilidad del dispositivo. [21]

En los materiales magnéticamente ordenados, la resistencia eléctrica se ve afectada de manera crucial por la dispersión de electrones en la subred magnética del cristal, que está formada por átomos cristalográficamente equivalentes con momentos magnéticos distintos de cero. La dispersión depende de las orientaciones relativas de los espines de los electrones y de esos momentos magnéticos: es más débil cuando son paralelos y más fuerte cuando son antiparalelos; es relativamente fuerte en el estado paramagnético, en el que los momentos magnéticos de los átomos tienen orientaciones aleatorias. [7] [22]
Para buenos conductores como el oro o el cobre, el nivel de Fermi se encuentra dentro de la banda sp , y la banda d está completamente llena. En los ferroimanes, la dependencia de la dispersión electrón-átomo en la orientación de sus momentos magnéticos está relacionada con el llenado de la banda responsable de las propiedades magnéticas del metal, por ejemplo, la banda 3 d para el hierro , el níquel o el cobalto . La banda d de los ferroimanes está dividida, ya que contiene un número diferente de electrones con espines dirigidos hacia arriba y hacia abajo. Por lo tanto, la densidad de estados electrónicos en el nivel de Fermi también es diferente para espines que apuntan en direcciones opuestas. El nivel de Fermi para electrones de espín mayoritario se encuentra dentro de la banda sp , y su transporte es similar en ferroimanes y metales no magnéticos. Para electrones de espín minoritario, las bandas sp y d están hibridadas, y el nivel de Fermi se encuentra dentro de la banda d . La banda spd hibridada tiene una alta densidad de estados, lo que da como resultado una dispersión más fuerte y, por lo tanto, un recorrido libre medio λ más corto para los electrones de espín minoritario que para los de espín mayoritario. En el níquel dopado con cobalto, la relación λ ↑ /λ ↓ puede alcanzar 20. [23]
Según la teoría de Drude , la conductividad es proporcional a λ, que varía de varios a varias decenas de nanómetros en películas metálicas delgadas. Los electrones "recuerdan" la dirección del espín dentro de la llamada longitud de relajación de espín (o longitud de difusión de espín), que puede superar significativamente el camino libre medio. El transporte dependiente del espín se refiere a la dependencia de la conductividad eléctrica de la dirección de espín de los portadores de carga. En los ferroimanes, se produce debido a las transiciones de electrones entre las bandas 4 s no divididas y 3 d divididas . [7]
En algunos materiales, la interacción entre electrones y átomos es más débil cuando sus momentos magnéticos son antiparalelos en lugar de paralelos. Una combinación de ambos tipos de materiales puede dar lugar a un efecto denominado GMR inverso. [7] [24]

La corriente eléctrica puede pasar a través de superredes magnéticas de dos maneras. En la geometría de corriente en el plano (CIP), la corriente fluye a lo largo de las capas y los electrodos se ubican en un lado de la estructura. En la configuración de corriente perpendicular al plano (CPP), la corriente pasa perpendicularmente a las capas y los electrodos se ubican en diferentes lados de la superred. [7] La geometría CPP da como resultado una GMR más del doble, pero es más difícil de implementar en la práctica que la configuración CIP. [25] [26]
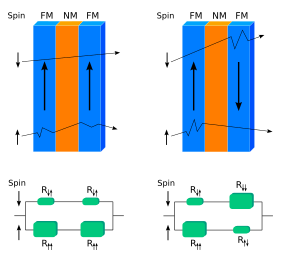
El orden magnético difiere en las superredes con interacción ferromagnética y antiferromagnética entre las capas. En el primer caso, las direcciones de magnetización son las mismas en diferentes capas ferromagnéticas en ausencia de campo magnético aplicado, mientras que en el segundo caso, las direcciones opuestas se alternan en la multicapa. Los electrones que viajan a través de la superred ferromagnética interactúan con ella mucho más débilmente cuando sus direcciones de giro son opuestas a la magnetización de la red que cuando son paralelas a ella. Esta anisotropía no se observa en la superred antiferromagnética; como resultado, dispersa electrones con mayor fuerza que la superred ferromagnética y exhibe una resistencia eléctrica más alta. [7]
Las aplicaciones del efecto GMR requieren una conmutación dinámica entre la magnetización paralela y antiparalela de las capas de una superred. En una primera aproximación, la densidad de energía de la interacción entre dos capas ferromagnéticas separadas por una capa no magnética es proporcional al producto escalar de sus magnetizaciones:
El coeficiente J es una función oscilatoria del espesor de la capa no magnética d s ; por lo tanto , J puede cambiar su magnitud y signo. Si el valor d s corresponde al estado antiparalelo, entonces un campo externo puede cambiar la superred del estado antiparalelo (alta resistencia) al estado paralelo (baja resistencia). La resistencia total de la estructura puede escribirse como
donde R 0 es la resistencia de la superred ferromagnética, ΔR es el incremento de GMR y θ es el ángulo entre las magnetizaciones de las capas adyacentes. [25]
El fenómeno GMR puede describirse utilizando dos canales de conductividad relacionados con el espín correspondientes a la conducción de electrones, para los cuales la resistencia es mínima o máxima. La relación entre ellos se define a menudo en términos del coeficiente de anisotropía de espín β. Este coeficiente puede definirse utilizando el mínimo y el máximo de la resistividad eléctrica específica ρ F± para la corriente polarizada por espín en la forma
donde ρ F es la resistividad media del ferroimán. [27]
Si la dispersión de los portadores de carga en la interfaz entre el metal ferromagnético y el no magnético es pequeña y la dirección de los espines de los electrones persiste durante el tiempo suficiente, es conveniente considerar un modelo en el que la resistencia total de la muestra sea una combinación de las resistencias de las capas magnéticas y no magnéticas.
En este modelo, existen dos canales de conducción para electrones con distintas direcciones de espín en relación con la magnetización de las capas. Por lo tanto, el circuito equivalente de la estructura GMR consta de dos conexiones paralelas correspondientes a cada uno de los canales. En este caso, el GMR se puede expresar como
Aquí el subíndice de R denota magnetización colineal y orientada de manera opuesta en capas, χ = b/a es la relación de espesores de las capas magnéticas y no magnéticas, y ρ N es la resistividad del metal no magnético. Esta expresión es aplicable tanto para estructuras CIP como CPP. Bajo la condición de que esta relación se pueda simplificar utilizando el coeficiente de asimetría de espín.
Un dispositivo de este tipo, con una resistencia que depende de la orientación del espín del electrón, se denomina válvula de espín . Está "abierta" si las magnetizaciones de sus capas son paralelas y "cerrada" en caso contrario. [28]
En 1993, Thierry Valet y Albert Fert presentaron un modelo para la magnetorresistencia gigante en la geometría CPP, basado en las ecuaciones de Boltzmann. En este modelo, el potencial químico dentro de la capa magnética se divide en dos funciones, correspondientes a electrones con espines paralelos y antiparalelos a la magnetización de la capa. Si la capa no magnética es suficientemente delgada, entonces en el campo externo E 0 las modificaciones del potencial electroquímico y del campo dentro de la muestra tomarán la forma
donde ℓ s es la longitud media de relajación de espín, y la coordenada z se mide desde el límite entre las capas magnética y no magnética (z < 0 corresponde al ferromagnético). [18] Por lo tanto, los electrones con un potencial químico mayor se acumularán en el límite del ferroimán. [29] Esto puede representarse por el potencial de acumulación de espín V AS o por la llamada resistencia de interfaz (inherente al límite entre un ferroimán y un material no magnético)
donde j es la densidad de corriente en la muestra, ℓ sN y ℓ sF son la longitud de la relajación de espín en un material no magnético y magnético, respectivamente. [30]
Muchas combinaciones de materiales exhiben GMR, [31] y las más comunes son las siguientes:
La magnetorresistencia depende de muchos parámetros como la geometría del dispositivo (CIP o CPP), su temperatura y los espesores de las capas ferromagnéticas y no magnéticas. A una temperatura de 4,2 K y un espesor de capas de cobalto de 1,5 nm, al aumentar el espesor de las capas de cobre dCu de 1 a 10 nm disminuyó δH de 80 a 10% en la geometría CIP. Mientras tanto, en la geometría CPP el máximo de δH ( 125%) se observó para dCu = 2,5 nm, y al aumentar dCu a 10 nm se redujo δH a 60% de manera oscilante. [33]
Cuando una superred de Co(1,2 nm)/Cu(1,1 nm) se calentó desde casi cero hasta 300 K, su δ H disminuyó del 40 al 20 % en la geometría CIP y del 100 al 55 % en la geometría CPP. [34]
Las capas no magnéticas pueden ser no metálicas. Por ejemplo, se demostró que el δ H alcanza el 40 % para las capas orgánicas a 11 K. [35] Las válvulas de espín de grafeno de varios diseños exhibieron un δ H de aproximadamente el 12 % a 7 K y el 10 % a 300 K, muy por debajo del límite teórico del 109 %. [36]
El efecto GMR se puede potenciar mediante filtros de espín que seleccionan electrones con una determinada orientación de espín; están hechos de metales como el cobalto. Para un filtro de espesor t, el cambio de conductividad ΔG se puede expresar como
donde ΔG SV es el cambio en la conductividad de la válvula de espín sin el filtro, ΔG f es el aumento máximo en la conductividad con el filtro y β es un parámetro del material del filtro. [37]
La GMR a menudo se clasifica según el tipo de dispositivos que exhiben el efecto. [38]
La GMR en películas fue observada por primera vez por Fert y Grünberg en un estudio de superredes compuestas de capas ferromagnéticas y no magnéticas. El espesor de las capas no magnéticas se eligió de tal manera que la interacción entre las capas fuera antiferromagnética y la magnetización en las capas magnéticas adyacentes fuera antiparalela. Entonces, un campo magnético externo podría hacer que los vectores de magnetización fueran paralelos, afectando así la resistencia eléctrica de la estructura. [10]
Las capas magnéticas en tales estructuras interactúan a través del acoplamiento antiferromagnético, lo que da como resultado la dependencia oscilante del GMR del espesor de la capa no magnética. En los primeros sensores de campo magnético que usaban superredes antiferromagnéticas, el campo de saturación era muy grande, hasta decenas de miles de oersteds , debido a la fuerte interacción antiferromagnética entre sus capas (hechas de cromo, hierro o cobalto) y los fuertes campos de anisotropía en ellas. Por lo tanto, la sensibilidad de los dispositivos era muy baja. El uso de permalloy para las capas magnéticas y plata para las no magnéticas redujo el campo de saturación a decenas de oersteds. [39]
En las válvulas de espín más exitosas, el efecto GMR se origina a partir de la polarización de intercambio. Están compuestas por una capa sensible, una capa "fija" y una capa antiferromagnética. La última capa congela la dirección de magnetización en la capa "fija". Las capas sensible y antiferromagnética se hacen delgadas para reducir la resistencia de la estructura. La válvula reacciona al campo magnético externo cambiando la dirección de magnetización en la capa sensible con respecto a la capa "fija". [39]
La principal diferencia de estas válvulas de espín con respecto a otros dispositivos GMR multicapa es la dependencia monótona de la amplitud del efecto sobre el espesor d N de las capas no magnéticas:
donde δ H0 es una constante de normalización, λ N es el camino libre medio de los electrones en el material no magnético, d 0 es el espesor efectivo que incluye la interacción entre capas. [38] [40] La dependencia del espesor de la capa ferromagnética se puede dar como:
Los parámetros tienen el mismo significado que en la ecuación anterior, pero ahora se refieren a la capa ferromagnética. [31]
La magnetorresistencia a la radiación magnética también se puede observar en ausencia de capas de acoplamiento antiferromagnético. En este caso, la magnetorresistencia resulta de las diferencias en las fuerzas coercitivas (por ejemplo, es menor para permalloy que para cobalto). En multicapas como permalloy/Cu/Co/Cu, el campo magnético externo cambia la dirección de la magnetización de saturación a paralela en campos fuertes y a antiparalela en campos débiles. Dichos sistemas presentan un campo de saturación menor y un δ H mayor que las superredes con acoplamiento antiferromagnético. [39] Se observa un efecto similar en las estructuras de Co/Cu. La existencia de estas estructuras significa que la magnetorresistencia a la radiación magnética no requiere acoplamiento entre capas y puede originarse a partir de una distribución de los momentos magnéticos que puede ser controlada por un campo externo. [41]
En la GMR inversa, la resistencia es mínima para la orientación antiparalela de la magnetización en las capas. La GMR inversa se observa cuando las capas magnéticas están compuestas de diferentes materiales, como NiCr/Cu/Co/Cu. La resistividad para electrones con espines opuestos se puede escribir como ; tiene diferentes valores, es decir, diferentes coeficientes β, para electrones de espín hacia arriba y hacia abajo. Si la capa de NiCr no es demasiado delgada, su contribución puede superar la de la capa de Co, lo que resulta en una GMR inversa. [24] Nótese que la inversión de la GMR depende del signo del producto de los coeficientes β en capas ferromagnéticas adyacentes, pero no de los signos de los coeficientes individuales. [34]
También se observa GMR inversa si la aleación de NiCr se reemplaza por níquel dopado con vanadio, pero no para el dopaje de níquel con hierro, cobalto, manganeso, oro o cobre. [42]
La GMR en aleaciones granulares de metales ferromagnéticos y no magnéticos se descubrió en 1992 y posteriormente se explicó por la dispersión dependiente del espín de los portadores de carga en la superficie y en la masa de los granos. Los granos forman cúmulos ferromagnéticos de unos 10 nm de diámetro incrustados en un metal no magnético, formando una especie de superred. Una condición necesaria para el efecto GMR en tales estructuras es la escasa solubilidad mutua de sus componentes (por ejemplo, cobalto y cobre). Sus propiedades dependen en gran medida de la medición y la temperatura de recocido. También pueden presentar GMR inversa. [32] [43]

Una de las principales aplicaciones de los materiales GMR es en sensores de campo magnético, por ejemplo, en unidades de disco duro [25] y biosensores [31] , así como detectores de oscilaciones en MEMS. [31] Un sensor típico basado en GMR consta de siete capas:
Las capas aglutinantes y protectoras suelen estar hechas de tantalio , y un material no magnético típico es el cobre. En la capa de detección, la magnetización puede ser reorientada por el campo magnético externo; normalmente está hecha de aleaciones de NiFe o cobalto. Se puede utilizar FeMn o NiMn para la capa antiferromagnética. La capa fija está hecha de un material magnético como el cobalto. Un sensor de este tipo tiene un bucle de histéresis asimétrico debido a la presencia de la capa fija magnéticamente dura. [44] [45]
Las válvulas de espín pueden exhibir magnetorresistencia anisotrópica, lo que conduce a una asimetría en la curva de sensibilidad. [46]
En las unidades de disco duro (HDD), la información se codifica utilizando dominios magnéticos , y un cambio en la dirección de su magnetización se asocia con el nivel lógico 1 mientras que ningún cambio representa un 0 lógico. Hay dos métodos de grabación: longitudinal y perpendicular.
En el método longitudinal, la magnetización es normal a la superficie. Se forma una región de transición (paredes de dominio) entre los dominios, en la que el campo magnético sale del material. Si la pared de dominio está ubicada en la interfaz de dos dominios del polo norte, entonces el campo se dirige hacia afuera, y para dos dominios del polo sur se dirige hacia adentro. Para leer la dirección del campo magnético sobre la pared de dominio, la dirección de magnetización se fija normal a la superficie en la capa antiferromagnética y paralela a la superficie en la capa de detección. Cambiar la dirección del campo magnético externo desvía la magnetización en la capa de detección. Cuando el campo tiende a alinear las magnetizaciones en las capas de detección y fija, la resistencia eléctrica del sensor disminuye, y viceversa. [47]

Una celda de memoria de acceso aleatorio magnetorresistiva (MRAM) tiene una estructura similar a la de un sensor de válvula de espín. El valor de los bits almacenados se puede codificar a través de la dirección de magnetización en la capa del sensor; se lee midiendo la resistencia de la estructura. Las ventajas de esta tecnología son la independencia de la fuente de alimentación (la información se conserva cuando se corta la alimentación debido a la barrera de potencial para reorientar la magnetización), el bajo consumo de energía y la alta velocidad. [25]
En una unidad de almacenamiento típica basada en GMR, una estructura CIP se ubica entre dos cables orientados perpendicularmente entre sí. Estos conductores se denominan líneas de filas y columnas. Los pulsos de corriente eléctrica que pasan a través de las líneas generan un campo magnético de vórtice, que afecta a la estructura GMR. Las líneas de campo tienen formas elipsoidales y la dirección del campo (en el sentido de las agujas del reloj o en sentido contrario) está determinada por la dirección de la corriente en la línea. En la estructura GMR, la magnetización está orientada a lo largo de la línea.
La dirección del campo producido por la línea de la columna es casi paralela a los momentos magnéticos, y no puede reorientarlos. La línea de la fila es perpendicular, e independientemente de la magnitud del campo puede rotar la magnetización solo 90°. Con el paso simultáneo de pulsos a lo largo de las líneas de la fila y la columna, el campo magnético total en la ubicación de la estructura GMR se dirigirá en un ángulo agudo con respecto a un punto y obtuso con respecto a otros. Si el valor del campo excede algún valor crítico, este último cambia su dirección.
Existen varios métodos de almacenamiento y lectura para la celda descrita. En un método, la información se almacena en la capa de detección; se lee a través de la medición de la resistencia y se borra al leer. En otro esquema, la información se mantiene en la capa fija, lo que requiere corrientes de registro más altas en comparación con las corrientes de lectura. [48]
La magnetorresistencia de túnel (TMR) es una extensión de la GMR de válvula de espín, en la que los electrones viajan con sus espines orientados perpendicularmente a las capas a través de una delgada barrera de túnel aislante (reemplazando el espaciador no ferromagnético). Esto permite lograr una mayor impedancia, un mayor valor de magnetorresistencia (~10× a temperatura ambiente) y una dependencia de temperatura insignificante. La TMR ha reemplazado a la GMR en las MRAM y las unidades de disco , en particular para altas densidades de área y grabación perpendicular. [49]
Los aisladores magnetorresistivos para la transmisión de señales sin contacto entre dos partes aisladas eléctricamente de circuitos eléctricos se demostraron por primera vez en 1997 como una alternativa a los optoaisladores . Un puente de Wheatstone de cuatro dispositivos GMR idénticos es insensible a un campo magnético uniforme y reacciona solo cuando las direcciones del campo son antiparalelas en los brazos vecinos del puente. Dichos dispositivos se informaron en 2003 y pueden usarse como rectificadores con una respuesta de frecuencia lineal. [31]