Un puente de Wheatstone es un circuito eléctrico que se utiliza para medir una resistencia eléctrica desconocida equilibrando dos patas de un circuito de puente , una de las cuales incluye el componente desconocido. El beneficio principal del circuito es su capacidad de proporcionar mediciones extremadamente precisas (en contraste con algo como un simple divisor de voltaje ). [1] Su funcionamiento es similar al del potenciómetro original .
El puente de Wheatstone fue inventado por Samuel Hunter Christie (a veces escrito "Christy") en 1833 y mejorado y popularizado por Sir Charles Wheatstone en 1843. [2] Uno de los usos iniciales del puente de Wheatstone fue para el análisis y comparación de suelos . [3]
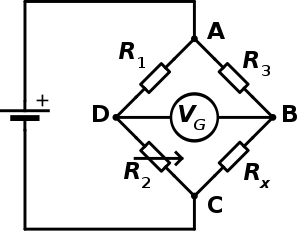
En la figura, R x es la resistencia fija, aunque desconocida, que se va a medir. R 1 , R 2 y R 3 son resistencias de resistencia conocida y la resistencia de R 2 es ajustable. La resistencia R 2 se ajusta hasta que el puente esté "equilibrado" y no fluya corriente a través del galvanómetro V g . En este punto, la diferencia de potencial entre los dos puntos medios (B y D) será cero. Por lo tanto, la relación de las dos resistencias en la pata conocida ( R 2 / R 1 ) es igual a la relación de las dos resistencias en la pata desconocida ( R x / R 3 ) . Si el puente está desequilibrado, la dirección de la corriente indica si R 2 es demasiado alta o demasiado baja.
En el punto de equilibrio,
La detección de corriente cero con un galvanómetro se puede realizar con una precisión extremadamente alta. Por lo tanto, si se conocen con alta precisión R 1 , R 2 y R 3 , entonces se puede medir R x con alta precisión. Cambios muy pequeños en R x alteran el equilibrio y se detectan fácilmente.
Alternativamente, si se conocen R 1 , R 2 y R 3 , pero R 2 no es ajustable, la diferencia de voltaje o el flujo de corriente a través del medidor se puede utilizar para calcular el valor de R x , utilizando las leyes de circuitos de Kirchhoff . Esta configuración se utiliza con frecuencia en mediciones con galgas extensométricas y termómetros de resistencia , ya que suele ser más rápido leer un nivel de voltaje en un medidor que ajustar una resistencia para poner a cero el voltaje.

En el punto de equilibrio, tanto la tensión como la corriente entre los dos puntos medios (B y D) son cero. Por lo tanto, I 1 = I 2 , I 3 = I x , V D = V B .
Debido a que V D = V B , entonces V DC = V BC y V AD = V AB .
Dividiendo las dos últimas ecuaciones por miembros y utilizando las igualdades de corrientes anteriores, entonces
En primer lugar, se utiliza la primera ley de Kirchhoff para encontrar las corrientes en las uniones B y D:
Luego, se utiliza la segunda ley de Kirchhoff para encontrar el voltaje en los bucles ABDA y BCDB:
Cuando el puente está equilibrado, entonces I G = 0 , por lo que el segundo conjunto de ecuaciones se puede reescribir como:
Luego, la ecuación (1) se divide por la ecuación (2) y la ecuación resultante se reordena, dando:
Como I 3 = I x e I 1 = I 2 son proporcionales según la primera ley de Kirchhoff, I 3 I 2 / I 1 I x se cancela en la ecuación anterior. Ahora se sabe que el valor deseado de R x se expresa como:
Por otra parte, si la resistencia del galvanómetro es lo suficientemente alta como para que I G sea despreciable, es posible calcular R x a partir de los otros tres valores de resistencia y la tensión de alimentación ( V S ), o la tensión de alimentación a partir de los cuatro valores de resistencia. Para ello, hay que calcular la tensión de cada divisor de potencial y restar uno del otro. Las ecuaciones para esto son:
donde V G es el voltaje del nodo D relativo al nodo B.
El puente de Wheatstone ilustra el concepto de una medición diferencial, que puede ser extremadamente precisa. Se pueden utilizar variaciones del puente de Wheatstone para medir la capacitancia , la inductancia , la impedancia y otras cantidades, como la cantidad de gases combustibles en una muestra, con un explosímetro . El puente de Kelvin se adaptó especialmente del puente de Wheatstone para medir resistencias muy bajas. En muchos casos, la importancia de medir la resistencia desconocida está relacionada con la medición del impacto de algún fenómeno físico (como la fuerza, la temperatura, la presión, etc.) lo que permite el uso del puente de Wheatstone para medir esos elementos indirectamente.
El concepto fue extendido a las mediciones de corriente alterna por James Clerk Maxwell en 1865 [4] y mejorado aún más comoPuente Blumlein de Alan Blumlein en la patente británica n.º 323.037, 1928.

El puente de Wheatstone es el puente fundamental, pero existen otras modificaciones que se pueden realizar para medir diversos tipos de resistencias cuando el puente de Wheatstone fundamental no es adecuado. Algunas de las modificaciones son: