Teoría de la ingeniería estructural

Figura de un perno sometido a corte . La figura superior ilustra un corte simple y la figura inferior un corte doble.

La ingeniería estructural depende de un conocimiento detallado de las cargas , la física y los materiales para comprender y predecir cómo las estructuras soportan y resisten el peso propio y las cargas impuestas. Para aplicar el conocimiento con éxito, los ingenieros estructurales necesitarán un conocimiento detallado de las matemáticas y de los códigos de diseño empíricos y teóricos pertinentes. También necesitarán saber sobre la resistencia a la corrosión de los materiales y las estructuras, especialmente cuando dichas estructuras están expuestas al entorno externo.

Los criterios que rigen el diseño de una estructura son la capacidad de servicio (criterios que definen si la estructura es capaz de cumplir adecuadamente su función) o la resistencia (criterios que definen si una estructura es capaz de soportar y resistir de forma segura sus cargas de diseño). Un ingeniero estructural diseña una estructura para que tenga la resistencia y la rigidez suficientes para cumplir con estos criterios.

Las cargas impuestas sobre las estructuras se soportan mediante fuerzas transmitidas a través de los elementos estructurales. Estas fuerzas pueden manifestarse como tensión (fuerza axial), compresión (fuerza axial), esfuerzo cortante y flexión o flexión (un momento flector es una fuerza multiplicada por una distancia o brazo de palanca, produciendo así un efecto de giro o par ).

Fortaleza

La resistencia depende de las propiedades del material. La resistencia de un material depende de su capacidad para soportar la tensión axial , la tensión cortante , la flexión y la torsión. La resistencia de un material se mide en fuerza por unidad de área (newtons por milímetro cuadrado o N/mm², o el equivalente megapascales o MPa en el sistema SI y, a menudo, libras por pulgada cuadrada psi en el sistema de unidades tradicionales de los Estados Unidos).

Una estructura no cumple el criterio de resistencia cuando la tensión (fuerza dividida por el área del material) inducida por la carga es mayor que la capacidad del material estructural para resistir la carga sin romperse, o cuando la deformación (porcentaje de extensión) es tan grande que el elemento ya no cumple su función ( rendimiento ).

Ver también:

Rigidez

La rigidez depende de las propiedades y la geometría del material . La rigidez de un elemento estructural de un material determinado es el producto del módulo de Young del material y el segundo momento de área del elemento . La rigidez se mide en fuerza por unidad de longitud (newtons por milímetro o N/mm) y es equivalente a la "constante de fuerza" de la Ley de Hooke .

La deflexión de una estructura bajo carga depende de su rigidez. La respuesta dinámica de una estructura a cargas dinámicas (la frecuencia natural de una estructura) también depende de su rigidez.

En una estructura formada por múltiples elementos estructurales en la que la superficie que distribuye las fuerzas entre los elementos es rígida, los elementos soportarán cargas en proporción a su rigidez relativa: cuanto más rígido sea un elemento, más carga atraerá. Esto significa que la relación carga/rigidez, que es la deflexión, permanece igual en dos elementos conectados (articulados). En una estructura en la que la superficie que distribuye las fuerzas entre los elementos es flexible (como una estructura con estructura de madera), los elementos soportarán cargas en proporción a sus áreas tributarias relativas.

Se considera que una estructura no cumple con los criterios de servicio elegidos si no es lo suficientemente rígida como para tener una deflexión o una respuesta dinámica bajo carga aceptablemente pequeñas.

La inversa de la rigidez es la flexibilidad .

Factores de seguridad

El diseño seguro de estructuras requiere un enfoque de diseño que tenga en cuenta la probabilidad estadística de falla de la estructura. Los códigos de diseño estructural se basan en el supuesto de que tanto las cargas como las resistencias de los materiales varían con una distribución normal . ^{[ cita requerida ]}

El trabajo del ingeniero estructural es garantizar que la probabilidad de superposición entre la distribución de cargas en una estructura y la distribución de la resistencia del material de una estructura sea aceptablemente pequeña (es imposible reducir esa probabilidad a cero).

Es normal aplicar un factor de seguridad parcial a las cargas y a las resistencias de los materiales, para diseñar utilizando percentiles 95 (dos desviaciones típicas de la media ). El factor de seguridad aplicado a la carga normalmente garantizará que en el 95% de los casos la carga real será menor que la carga de diseño, mientras que el factor aplicado a la resistencia garantiza que en el 95% de los casos la resistencia real será mayor que la resistencia de diseño.

Los factores de seguridad para la resistencia del material varían dependiendo del material y del uso que se le dé y de los códigos de diseño aplicables en el país o la región.

Un enfoque más sofisticado para modelar la seguridad estructural es basarse en la confiabilidad estructural , en la que tanto las cargas como las resistencias se modelan como variables probabilísticas. ^{[1] [2]} Sin embargo, el uso de este enfoque requiere un modelado detallado de la distribución de cargas y resistencias. Además, sus cálculos requieren un mayor uso de recursos computacionales.

Casos de carga

Un caso de carga es una combinación de distintos tipos de cargas con factores de seguridad aplicados a ellas. Se comprueba la resistencia y la capacidad de servicio de una estructura frente a todos los casos de carga que es probable que experimente durante su vida útil.

Los casos de carga típicos para el diseño de resistencia (casos de carga máxima; ULS) son:

1,2 x Carga muerta + 1,6 x Carga viva

1,2 x Carga muerta + 1,2 x Carga viva + 1,2 x Carga de viento

Un caso de carga típico para el diseño para capacidad de servicio (casos de carga característicos; SLS) es:

1.0 x Carga muerta + 1.0 x Carga viva

Se utilizarían distintos casos de carga para distintas condiciones de carga. Por ejemplo, en el caso de un diseño para incendios, se puede utilizar un caso de carga de 1,0 x Carga muerta + 0,8 x Carga viva , ya que es razonable suponer que todos han abandonado el edificio si se produce un incendio.

En edificios de varios pisos, es normal reducir la carga viva total dependiendo del número de pisos soportados, ya que la probabilidad de que se aplique la carga máxima a todos los pisos simultáneamente es insignificante.

No es raro que en el diseño de edificios de gran tamaño se requieran considerar cientos de casos de carga diferentes.

Leyes del movimiento de Newton

Las leyes naturales más importantes para la ingeniería estructural son las Leyes del Movimiento de Newton.

La primera ley de Newton establece que todo cuerpo persevera en su estado de reposo o de movimiento uniforme y rectilíneo, salvo en la medida en que se vea obligado a cambiar su estado por una fuerza impresa.

La segunda ley de Newton establece que la tasa de cambio de momento de un cuerpo es proporcional a la fuerza resultante que actúa sobre el cuerpo y tiene la misma dirección. Matemáticamente, F=ma (fuerza = masa x aceleración).

La tercera ley de Newton establece que todas las fuerzas ocurren en pares, y estas dos fuerzas son iguales en magnitud y opuestas en dirección.

Con estas leyes es posible entender las fuerzas que actúan sobre una estructura y cómo ésta las resistirá. La Tercera Ley exige que para que una estructura sea estable todas las fuerzas internas y externas deben estar en equilibrio . Esto significa que la suma de todas las fuerzas internas y externas en un diagrama de cuerpo libre debe ser cero:

• ${\displaystyle \sum {\vec {F}}=0}$:la suma vectorial de las fuerzas que actúan sobre el cuerpo es igual a cero. Esto se traduce en

Σ H = 0: la suma de los componentes horizontales de las fuerzas es igual a cero;

Σ V = 0: la suma de los componentes verticales de las fuerzas es igual a cero;

• ${\displaystyle \sum {\vec {M}}=0}$:la suma de los momentos (alrededor de un punto arbitrario) de todas las fuerzas es igual a cero.

Determinación estática

Un ingeniero estructural debe comprender las fuerzas internas y externas de un sistema estructural que consta de elementos estructurales y nodos en sus intersecciones.

Una estructura estáticamente determinada se puede analizar completamente considerando únicamente el equilibrio, a partir de las Leyes del Movimiento de Newton.

Una estructura estáticamente indeterminada tiene más incógnitas que las ecuaciones que se pueden obtener con consideraciones de equilibrio (ver ecuaciones simultáneas ). Un sistema de este tipo se puede resolver considerando ecuaciones de compatibilidad entre geometría y deflexiones además de ecuaciones de equilibrio, o utilizando trabajo virtual .

Si un sistema está formado por barras, uniones articuladas y reacciones de apoyo, entonces no puede ser estáticamente determinado si no se cumple la siguiente relación: ${\displaystyle b}$ ${\displaystyle j}$ ${\displaystyle r}$

${\displaystyle r+b=2j}$

Incluso si esta relación se mantiene, una estructura puede organizarse de tal manera que sea estáticamente indeterminada. ^[3]

Elasticidad

Gran parte del diseño de ingeniería se basa en el supuesto de que los materiales se comportan de forma elástica. Para la mayoría de los materiales, este supuesto es incorrecto, pero la evidencia empírica ha demostrado que el diseño que utiliza este supuesto puede ser seguro. Los materiales que son elásticos obedecen la Ley de Hooke y no se produce plasticidad.

Para los sistemas que obedecen la Ley de Hooke, la extensión producida es directamente proporcional a la carga:

${\displaystyle {\vec {\mathbf {F} }}=k{\vec {\mathbf {x} }}\ }$

dónde

x es la distancia que el resorte se ha estirado o comprimido desde la posición de equilibrio, que es la posición en la que el resorte descansaría naturalmente [generalmente en metros],

F es la fuerza restauradora ejercida por el material [generalmente en newtons], y

k es la constante de fuerza (o constante del resorte ). Es la rigidez del resorte. La constante tiene unidades de fuerza por unidad de longitud (generalmente en newtons por metro ).

Plasticidad

Comparación de los criterios de Tresca y Von Mises

Algunos diseños se basan en el supuesto de que los materiales se comportarán plásticamente . ^[4] Un material plástico es aquel que no obedece la Ley de Hooke y, por lo tanto, la deformación no es proporcional a la carga aplicada. Los materiales plásticos son materiales dúctiles . La teoría de la plasticidad se puede utilizar para algunas estructuras de hormigón armado suponiendo que están poco reforzadas, lo que significa que el refuerzo de acero falla antes que el hormigón.

La teoría de la plasticidad establece que el punto en el que una estructura colapsa (alcanza el límite elástico) se encuentra entre un límite superior y uno inferior de la carga, definido de la siguiente manera:

• Si, para una carga externa dada, es posible encontrar una distribución de momentos que satisfaga los requisitos de equilibrio, sin que el momento exceda el momento de fluencia en ninguna ubicación, y si se satisfacen las condiciones de contorno, entonces la carga dada es un límite inferior para la carga de colapso.
• Si, para un pequeño incremento de desplazamiento, el trabajo interno realizado por la estructura, asumiendo que el momento en cada articulación plástica es igual al momento de fluencia y que se satisfacen las condiciones de contorno, es igual al trabajo externo realizado por la carga dada para ese mismo pequeño incremento de desplazamiento, entonces esa carga es un límite superior de la carga de colapso.

Si se encuentra la carga de colapso correcta, los dos métodos darán el mismo resultado para la carga de colapso. ^[5]

La teoría de la plasticidad depende de una correcta comprensión de cuándo se producirá la fluencia. Existen varios modelos diferentes para la distribución de la tensión y aproximaciones a la superficie de fluencia de los materiales plásticos: ^[6]

• Círculo de Mohr
• Criterio de rendimiento de von Mises
• Henri Tresca

Ecuación de la viga de Euler-Bernoulli

Deflexión de un voladizo bajo una carga puntual (f) en ingeniería

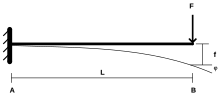
La ecuación de Euler-Bernoulli para vigas define el comportamiento de un elemento de viga (véase más abajo). Se basa en cinco supuestos:

1. La mecánica del medio continuo es válida para una viga en flexión.
2. La tensión en una sección transversal varía linealmente en la dirección de flexión y es cero en el centroide de cada sección transversal .
3. El momento de flexión en una sección transversal particular varía linealmente con la segunda derivada de la forma desviada en esa ubicación.
4. La viga está compuesta de un material isótropo.
5. La carga aplicada es ortogonal al eje neutro de la viga y actúa en un único plano.

Una versión simplificada de la ecuación de la viga de Euler-Bernoulli es:

${\displaystyle {\frac {d^{2}}{dx^{2}}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)=q(x).\,}$

Aquí está la deflexión y es una carga por unidad de longitud. es el módulo elástico y es el segundo momento del área , el producto de estos da la rigidez a la flexión de la viga. ${\displaystyle w}$ ${\displaystyle q(x)}$ ${\displaystyle E}$ ${\displaystyle I}$

Esta ecuación es muy común en la práctica de ingeniería: describe la desviación de una viga estática y uniforme.

Los derivados sucesivos de tienen significados importantes: ${\displaystyle w}$

• ${\displaystyle \textstyle {w}\,}$ es la deflexión.

• ${\displaystyle \textstyle {\frac {dw}{dx}}\,}$ es la pendiente de la viga.

• ${\displaystyle \textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,}$ es el momento flector en la viga.

• ${\displaystyle \textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,}$ es la fuerza cortante en la viga.

Un momento flector se manifiesta como una fuerza de tracción y una fuerza de compresión que actúan como un par en una viga. Las tensiones causadas por estas fuerzas se pueden representar mediante:

${\displaystyle \sigma ={\frac {My}{I}}=-Ey{\frac {d^{2}w}{dx^{2}}}\,}$

donde es la tensión, es el momento flector, es la distancia desde el eje neutro de la viga hasta el punto en consideración y es el segundo momento del área . A menudo, la ecuación se simplifica al momento dividido por el módulo de sección , que es . Esta ecuación permite a un ingeniero estructural evaluar la tensión en un elemento estructural cuando se somete a un momento flector. ${\displaystyle \sigma }$ ${\displaystyle M}$ ${\displaystyle y}$ ${\displaystyle I}$ ${\displaystyle S}$ ${\displaystyle I/y}$

Pandeo

Una columna bajo una carga axial céntrica que presenta la deformación característica de pandeo.

Los elementos estructurales sometidos a fuerzas de compresión pueden deformarse significativamente debido al efecto desestabilizador de dicha carga. El efecto puede iniciarse o exacerbarse por posibles imprecisiones en la fabricación o construcción.

La fórmula de pandeo de Euler define la fuerza de compresión axial que provocará que un puntal (o columna) falle por pandeo.

${\displaystyle F={\frac {\pi ^{2}EI}{(Kl)^{2}}}}$

dónde

${\displaystyle F}$= fuerza máxima o crítica (carga vertical sobre la columna),

${\displaystyle E}$= módulo de elasticidad ,

${\displaystyle I}$= momento de inercia del área , o segundo momento del área

${\displaystyle l}$= longitud de columna sin soporte,

${\displaystyle K}$= factor de longitud efectiva de la columna, cuyo valor depende de las condiciones de apoyo de los extremos de la columna, como se indica a continuación.

Para ambos extremos fijados con pasadores (bisagrados, libres para girar), = 1,0. ${\displaystyle K}$

Para ambos extremos fijos, = 0,50. ${\displaystyle K}$

Para un extremo fijo y el otro extremo fijado con pasador, 0,70. ${\displaystyle K\approx }$

Para un extremo fijo y el otro extremo libre para moverse lateralmente, = 2,0. ${\displaystyle K}$

Este valor a veces se expresa para fines de diseño como una tensión de pandeo crítica .

${\displaystyle \sigma ={\frac {\pi ^{2}E}{({\frac {Kl}{r}})^{2}}}}$

dónde

${\displaystyle \sigma }$= tensión máxima o crítica

${\displaystyle r}$= el radio de giro mínimo de la sección transversal

Otras formas de pandeo incluyen el pandeo torsional lateral, donde el ala de compresión de una viga en flexión se pandea, y el pandeo de elementos de placa en vigas de placa debido a la compresión en el plano de la placa.

Véase también

• Análisis estructural
• Software de ingeniería estructural

Referencias

1. Melchers, RE (2002), "Análisis y predicción de confiabilidad estructural", 2.ª ed., John Wiley, Chichester, Reino Unido .
2. Piryonesi, Sayed Madeh; Tavakolan, Mehdi (9 de enero de 2017). "Un modelo de programación matemática para resolver problemas de optimización de costo-seguridad (CSO) en el mantenimiento de estructuras". KSCE Journal of Civil Engineering . 21 (6): 2226–2234. Bibcode :2017KSJCE..21.2226P. doi :10.1007/s12205-017-0531-z.
3. Dym, Clive L. (1997). Modelado y análisis estructural . Cambridge University Press. pág. 98. ISBN 0-521-49536-9.
4. Heyman, Jacques (1998). Análisis estructural: un enfoque histórico . Cambridge University Press. ISBN 0-521-62249-2.
5. Nilson, Arthur H.; Darwin, David; Dolan, Charles W. (2004). Diseño de estructuras de hormigón . McGraw-Hill Professional. pág. 486. ISBN 0-07-248305-9.
6. Heyman, Jacques (1999). La ciencia de la ingeniería estructural. Imperial College Press. ISBN 1-86094-189-3.

• Castigliano, Carlo Alberto (traductor: Andrews, Ewart S.) (1966). La teoría del equilibrio de sistemas elásticos y sus aplicaciones. Dover Publications.
• Dym, Clive L. (1997). Modelado y análisis estructural . Cambridge University Press. ISBN 0-521-49536-9 . 
• Dugas, René (1988). Una historia de la mecánica . Courier Dover Publications. ISBN 0-486-65632-2 . 
• Hewson, Nigel R. (2003). Puentes de hormigón pretensado: diseño y construcción . Thomas Telford. ISBN 0-7277-2774-5 . 
• Heyman, Jacques (1998). Análisis estructural: un enfoque histórico . Cambridge University Press. ISBN 0-521-62249-2 . 
• Heyman, Jacques (1999). La ciencia de la ingeniería estructural . Imperial College Press. ISBN 1-86094-189-3 . 
• Hognestad, E. Un estudio de la combinación de flexión y carga axial en elementos de hormigón armado . Universidad de Illinois, Estación experimental de ingeniería, Boletín de la serie N.º 399.
• Jennings, Alan (2004) Estructuras: de la teoría a la práctica. Taylor & Francis. ISBN 978-0-415-26843-1 . 
• Leonhardt, A. (1964). Vom Caementum zum Spannbeton, Banda III (Del cemento al hormigón pretensado) . Bauverlag GmbH.
• MacNeal, Richard H. (1994). Elementos finitos: su diseño y rendimiento . Marcel Dekker. ISBN 0-8247-9162-2 . 
• Mörsch, E. (Stuttgart, 1908). Der Eisenbetonbau, seine Theorie und Anwendung, (Construcción de hormigón armado, su teoría y aplicación) . Konrad Wittwer, 3ª edición.
• Nedwell, PJ; Swamy, RN (ed) (1994). Ferrocemento: Actas del quinto simposio internacional . Taylor & Francis. ISBN 0-419-19700-1 . 
• Newton, Isaac; Leseur, Thomas; Jacquier, François (1822). Philosophiæ Naturalis Principia Mathematica. Universidad de Oxford.
• Nilson, Arthur H.; Darwin, David; Dolan, Charles W. (2004). Diseño de estructuras de hormigón . McGraw-Hill Professional. ISBN 0-07-248305-9 . 
• Rozhanskaya, Mariam; Levinova, IS (1996). "Estática" en Morelon, Régis y Rashed, Roshdi (1996). Enciclopedia de la historia de la ciencia árabe , vol. 2-3 , Routledge. ISBN 0-415-02063-8 
• Schlaich, J., K. Schäfer, M. Jennewein (1987). "Hacia un diseño consistente de hormigón estructural". PCI Journal , Informe especial, vol. 32, n.º 3.
• Scott, Richard (2001). Tras el desastre de Tacoma: puentes colgantes y la búsqueda de estabilidad aerodinámica . Publicaciones de la ASCE. ISBN 0-7844-0542-5 . 
• Turner, J.; Clough, RW; Martin, HC; Topp, LJ (1956). "Rigidez y deflexión de estructuras complejas". Revista de ciencia aeronáutica, número 23 .
• Virdi, KS (2000). Carga anormal en estructuras: modelado experimental y numérico . Taylor & Francis. ISBN 0-419-25960-0 .