En matemáticas combinatorias , la teoría de especies combinatorias es un método abstracto y sistemático para derivar las funciones generadoras de estructuras discretas, que permite no solo contar estas estructuras sino también dar pruebas biyectivas que las involucran. Ejemplos de especies combinatorias son los grafos (finitos) , las permutaciones , los árboles , etc.; cada uno de estos tiene una función generadora asociada que cuenta cuántas estructuras hay de un cierto tamaño. Un objetivo de la teoría de especies es poder analizar estructuras complicadas describiéndolas en términos de transformaciones y combinaciones de estructuras más simples. Estas operaciones corresponden a manipulaciones equivalentes de funciones generadoras, por lo que producir tales funciones para estructuras complicadas es mucho más fácil que con otros métodos. La teoría fue introducida, cuidadosamente elaborada y aplicada por investigadores canadienses en torno a André Joyal .
El poder de la teoría proviene de su nivel de abstracción. El "formato de descripción" de una estructura (como una lista de adyacencia versus una matriz de adyacencia para grafos) es irrelevante, porque las especies son puramente algebraicas. La teoría de categorías proporciona un lenguaje útil para los conceptos que surgen aquí, pero no es necesario comprender las categorías antes de poder trabajar con especies.
La categoría de especie es equivalente a la categoría de secuencias simétricas en conjuntos finitos. [1]
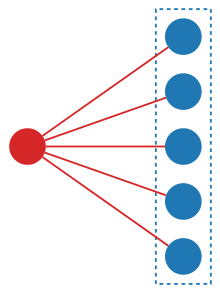
Cualquier especie consiste en estructuras combinatorias individuales construidas sobre los elementos de algún conjunto finito: por ejemplo, un grafo combinatorio es una estructura de aristas entre un conjunto dado de vértices, y la especie de grafos incluye todos los grafos en todos los conjuntos finitos. Además, un miembro de una especie puede tener su conjunto subyacente reetiquetado por los elementos de cualquier otro conjunto equinumeroso, por ejemplo, reetiquetar los vértices de un grafo da "la misma estructura de grafo" en los nuevos vértices, es decir, un grafo isomorfo .
Esto nos lleva a la definición formal de una especie combinatoria . Sea la categoría de conjuntos finitos , siendo los morfismos de la categoría las biyecciones entre estos conjuntos. Una especie es un funtor [2]
Para cada conjunto finito A en , el conjunto finito F [ A ] [nota 1] se denomina conjunto de F -estructuras en A , o conjunto de estructuras de especie F en A . Además, por la definición de un funtor, si φ es una biyección entre los conjuntos A y B , entonces F [φ] es una biyección entre los conjuntos de F -estructuras F [ A ] y F [ B ], denominada transporte de F-estructuras a lo largo de φ . [3]
Por ejemplo, la "especie de permutaciones" [4] asigna cada conjunto finito A al conjunto S [ A ] de todas las permutaciones de A (todas las formas de ordenar A en una lista), y cada biyección f de A a otro conjunto B induce naturalmente una biyección (un reetiquetado) que lleva cada permutación de A a una permutación correspondiente de B , es decir, una biyección . De manera similar, la "especie de particiones" se puede definir asignando a cada conjunto finito el conjunto de todas sus particiones , y la "especie de conjunto potencia" asigna a cada conjunto finito su conjunto potencia . El diagrama adyacente muestra una estructura (representada por un punto rojo) construida sobre un conjunto de cinco elementos distintos (representados por puntos azules); una estructura correspondiente podría construirse a partir de cinco elementos cualesquiera.
Dos conjuntos finitos están en biyección siempre que tengan la misma cardinalidad (número de elementos); por lo tanto, por definición, los conjuntos de especies correspondientes también están en biyección, y la cardinalidad (finita) de depende solo de la cardinalidad de A . [nota 2] En particular, la serie generadora exponencial F ( x ) de una especie F se puede definir: [5]
donde es la cardinalidad de para cualquier conjunto A que tenga n elementos; por ejemplo, .
Algunos ejemplos: escribir ,
La aritmética sobre funciones generadoras corresponde a ciertas operaciones "naturales" sobre especies. Las operaciones básicas son la suma, la multiplicación, la composición y la diferenciación; también es necesario definir la igualdad sobre especies. La teoría de categorías ya tiene una forma de describir cuándo dos funtores son equivalentes: un isomorfismo natural . En este contexto, simplemente significa que para cada A hay una biyección entre las estructuras F sobre A y las estructuras G sobre A , que se "comporta bien" en su interacción con el transporte. Las especies con la misma función generadora pueden no ser isomorfas, pero las especies isomorfas siempre tienen la misma función generadora.
La adición de especies se define por la unión disjunta de conjuntos, y corresponde a una elección entre estructuras. [6] Para las especies F y G , defina ( F + G )[ A ] como la unión disjunta (también escrita "+") de F [ A ] y G [ A ]. De ello se deduce que ( F + G )( x ) = F ( x ) + G ( x ). Como demostración, tome E + como la especie de conjuntos no vacíos, cuya función generadora es E + ( x ) = e x − 1, y 1 como la especie del conjunto vacío , cuya función generadora es 1 ( x ) = 1. De ello se deduce que la suma de las dos especies E = 1 + E + : en palabras, "un conjunto es vacío o no vacío". Ecuaciones como ésta pueden leerse como referencias a una única estructura, así como a toda la colección de estructuras.
La multiplicación de especies es un poco más complicada. Es posible tomar como definición el producto cartesiano de conjuntos, pero la interpretación combinatoria de esto no es del todo correcta (véase más adelante el uso de este tipo de producto). En lugar de juntar dos estructuras no relacionadas en el mismo conjunto, el operador de multiplicación utiliza la idea de dividir el conjunto en dos componentes, construyendo una estructura F en uno y una estructura G en el otro. [7]
Se trata de una unión disjunta sobre todas las particiones binarias posibles de A. Es sencillo demostrar que la multiplicación es asociativa y conmutativa ( salvo isomorfismo ), y distributiva sobre la suma. En cuanto a la serie generadora, ( F · G )( x ) = F ( x ) G ( x ).
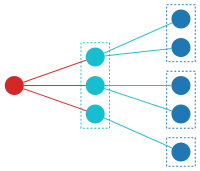
El diagrama siguiente muestra una posible estructura ( F · G ) en un conjunto con cinco elementos. La estructura F (roja) toma tres elementos del conjunto base, y la estructura G (azul claro) toma el resto. Otras estructuras tendrán F y G dividiendo el conjunto de una manera diferente. El conjunto ( F · G )[ A ], donde A es el conjunto base, es la unión disjunta de todas esas estructuras.

La adición y multiplicación de especies son la expresión más completa de las reglas de suma y producto del conteo. [ cita requerida ]
La composición , también llamada sustitución, es más complicada. La idea básica es reemplazar componentes de F con estructuras G , formando ( F ∘ G ). [8] Al igual que con la multiplicación, esto se hace dividiendo el conjunto de entrada A ; los subconjuntos disjuntos se dan a G para formar estructuras G , y el conjunto de subconjuntos se da a F , para formar la estructura F que une las estructuras G . Es necesario que G asigne el conjunto vacío a sí mismo para que la composición funcione. La definición formal es:
Aquí, P es la especie de particiones, por lo que P [ A ] es el conjunto de todas las particiones de A . Esta definición dice que un elemento de ( F ∘ G )[ A ] está formado por una estructura F en alguna partición de A y una estructura G en cada componente de la partición. La serie generadora es .
A continuación se muestra una de esas estructuras. Tres estructuras G (azul claro) dividen el conjunto base de cinco elementos entre ellas; luego, se construye una estructura F (roja) para conectar las estructuras G.
Estas dos últimas operaciones pueden ilustrarse con el ejemplo de los árboles. Primero, definamos X como la especie "singleton" cuya serie generadora es X ( x ) = x . Luego, la especie Ar de árboles con raíz (del francés " arborescence ") se define recursivamente por Ar = X · E ( Ar ). Esta ecuación dice que un árbol consiste en una sola raíz y un conjunto de (sub)árboles. La recursión no necesita un caso base explícito: solo genera árboles en el contexto de ser aplicada a algún conjunto finito. Una forma de pensar en esto es que el funtor Ar se está aplicando repetidamente a un "suministro" de elementos del conjunto - cada vez, un elemento es tomado por X , y los otros distribuidos por E entre los subárboles Ar , hasta que no hay más elementos para dar a E . Esto muestra que las descripciones algebraicas de las especies son bastante diferentes de las especificaciones de tipo en lenguajes de programación como Haskell .
De la misma manera, la especie P puede caracterizarse como P = E ( E + ): "una partición es un conjunto disjunto de conjuntos no vacíos (que utiliza todos los elementos del conjunto de entrada)". La serie generadora exponencial para P es , que es la serie para los números de Bell .
La diferenciación de especies corresponde intuitivamente a la construcción de "estructuras con un agujero", como se muestra en la siguiente ilustración.

Formalmente, [9]
¿Dónde está algún nuevo elemento distinguido que no está presente en ?
Para diferenciar las series exponenciales asociadas, la secuencia de coeficientes debe desplazarse un lugar hacia la "izquierda" (perdiendo el primer término). Esto sugiere una definición para las especies: F' [ A ] = F [ A + {*}], donde {*} es un conjunto unitario y "+" es una unión disjunta. Las partes más avanzadas de la teoría de las especies utilizan ampliamente la diferenciación para construir y resolver ecuaciones diferenciales sobre especies y series. La idea de agregar (o eliminar) una sola parte de una estructura es poderosa: puede usarse para establecer relaciones entre especies aparentemente desconectadas.
Por ejemplo, considere una estructura de la especie L de órdenes lineales: listas de elementos del conjunto básico. Al eliminar un elemento de una lista, esta se divide en dos partes (posiblemente vacías); en símbolos, esto es L' = L · L . La función generadora exponencial de L es L ( x ) = 1/(1 − x ), y, de hecho:
Las fórmulas de diferenciación generalizada se encuentran en una investigación previa de NG de Bruijn, publicada en 1964.
La especie C de permutaciones cíclicas lleva un conjunto A al conjunto de todos los ciclos en A . Quitar un solo elemento de un ciclo lo reduce a una lista: C' = L . Podemos integrar la función generadora de L para producir eso para C .
Un buen ejemplo de integración de una especie es la finalización de una línea (coordinada por un campo) con el punto infinito y la obtención de una línea proyectiva.
Existe una variedad de otras manipulaciones que pueden realizarse sobre las especies. Estas son necesarias para expresar estructuras más complejas, como grafos dirigidos o bigrafos .
El apuntamiento selecciona un solo elemento en una estructura. [10] Dada una especie F , la especie apuntada correspondiente F • se define por F • [ A ] = A × F [ A ]. Por lo tanto, cada F • -estructura es una F -estructura con un elemento distinguido. El apuntamiento está relacionado con la diferenciación por la relación F • = X · F' , por lo que F • ( x ) = x F' ( x ). La especie de conjuntos apuntados , E • , es particularmente importante como un bloque de construcción para muchas de las construcciones más complejas.
El producto cartesiano de dos especies [ cita requerida ] es una especie que puede construir dos estructuras en el mismo conjunto al mismo tiempo. Es diferente del operador de multiplicación ordinario en que todos los elementos del conjunto base son compartidos entre las dos estructuras. Una ( F × G )-estructura puede verse como una superposición de una F -estructura y una G -estructura. Los bigrafos podrían describirse como la superposición de un grafo y un conjunto de árboles: cada nodo del bigrafo es parte de un grafo y, al mismo tiempo, parte de algún árbol que describe cómo se anidan los nodos. La función generadora ( F × G )( x ) es el producto Hadamard o coeficiente a coeficiente de F ( x ) y G ( x ).
Se puede considerar que la especie E • × E • realiza dos selecciones independientes del conjunto base. Los dos puntos podrían coincidir, a diferencia de X · X · E , donde se ven obligados a ser diferentes.
Como funtores, las especies F y G pueden combinarse por composición funtorial : [ cita requerida ] (se utiliza el símbolo de caja, porque el círculo ya se utiliza para la sustitución). Esto construye una F -estructura en el conjunto de todas las G -estructuras en el conjunto A . Por ejemplo, si F es el funtor que eleva un conjunto a su conjunto potencia, una estructura de la especie compuesta es algún subconjunto de las G -estructuras en A . Si ahora tomamos G como E • × E • de arriba, obtenemos la especie de grafos dirigidos, con bucles propios permitidos. (Un grafo dirigido es un conjunto de aristas, y las aristas son pares de nodos: por lo que un grafo es un subconjunto del conjunto de pares de elementos del conjunto de nodos A .) Otras familias de grafos, así como muchas otras estructuras, pueden definirse de esta manera.
Las operaciones con especies son soportadas por SageMath [11] y, usando un paquete especial, también por Haskell . [12] [13]
Si se reemplaza “conjuntos finitos con biyecciones” por “espacios vectoriales finitos con transformaciones lineales”, entonces se obtiene la noción de functor polinomial (después de imponer alguna condición de finitud). [ cita requerida ]