Leyes de circuitos de Kirchhoff

Las leyes de circuitos de Kirchhoff son dos igualdades que tratan la diferencia de corriente y potencial (comúnmente conocida como voltaje) en el modelo de elementos concentrados de circuitos eléctricos . Fueron descritas por primera vez en 1845 por el físico alemán Gustav Kirchhoff . ^[1] Esto generalizó el trabajo de Georg Ohm y precedió al trabajo de James Clerk Maxwell . Ampliamente utilizadas en ingeniería eléctrica , también se denominan reglas de Kirchhoff o simplemente leyes de Kirchhoff . Estas leyes se pueden aplicar en los dominios del tiempo y la frecuencia y forman la base para el análisis de redes .

Ambas leyes de Kirchhoff pueden entenderse como corolarios de las ecuaciones de Maxwell en el límite de baja frecuencia. Son precisas para circuitos de corriente continua y para circuitos de corriente alterna en frecuencias en las que las longitudes de onda de la radiación electromagnética son muy grandes en comparación con los circuitos.

Ley de corriente de Kirchhoff

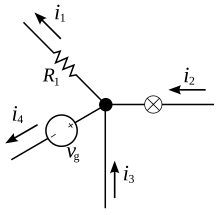
Esta ley, también llamada primera ley de Kirchhoff o regla de unión de Kirchhoff , establece que, para cualquier nodo (unión) en un circuito eléctrico , la suma de las corrientes que fluyen hacia ese nodo es igual a la suma de las corrientes que fluyen hacia afuera de ese nodo; o equivalentemente:

La suma algebraica de las corrientes en una red de conductores que se encuentran en un punto es cero.

Recordando que la corriente es una cantidad con signo (positivo o negativo) que refleja la dirección hacia o desde un nodo, este principio se puede expresar sucintamente como: donde $n$ es el número total de ramas con corrientes que fluyen hacia o desde el nodo. $\suma _{i=1}^{n}I_{i}=0$

Las leyes de circuitos de Kirchhoff se obtuvieron originalmente a partir de resultados experimentales. Sin embargo, la ley de corriente puede verse como una extensión de la conservación de la carga , ya que la carga es el producto de la corriente por el tiempo que la corriente ha estado fluyendo. Si la carga neta en una región es constante, la ley de corriente se mantendrá en los límites de la región. ^[2]^[3] Esto significa que la ley de corriente se basa en el hecho de que la carga neta en los cables y componentes es constante.

Usos

La mayoría de los programas de simulación de circuitos , como SPICE , utilizan una versión matricial de la ley de corrientes de Kirchhoff . La ley de corrientes se utiliza junto con la ley de Ohm para realizar análisis nodales .

La presente ley es aplicable a cualquier red agrupada independientemente de su naturaleza: unilateral o bilateral, activa o pasiva, lineal o no lineal.

Ley de voltaje de Kirchhoff

Esta ley, también llamada segunda ley de Kirchhoff o regla de bucles de Kirchhoff , establece lo siguiente:

La suma dirigida de las diferencias de potencial (voltajes) alrededor de cualquier bucle cerrado es cero.

De manera similar a la ley de corriente de Kirchhoff, la ley de voltaje puede enunciarse como: $\suma _{i=1}^{n}V_{i}=0$

Aquí, $n$ es el número total de voltajes medidos.

Derivación de la ley de voltaje de Kirchhoff

Una derivación similar se puede encontrar en The Feynman Lectures on Physics, Volumen II, Capítulo 22: Circuitos de CA. [ ^3]

Consideremos un circuito arbitrario. Aproximamos el circuito con elementos concentrados, de modo que los campos magnéticos variables en el tiempo estén contenidos en cada componente y el campo en la región exterior al circuito sea despreciable. Con base en este supuesto, la ecuación de Maxwell-Faraday revela que en la región exterior. Si cada uno de los componentes tiene un volumen finito, entonces la región exterior está simplemente conexa y, por lo tanto, el campo eléctrico es conservativo en esa región. Por lo tanto, para cualquier bucle en el circuito, encontramos que donde son caminos alrededor del exterior de cada uno de los componentes, de un terminal a otro. $\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {0}$ $\sum _{i}V_{i}=-\sum _{i}\int _{{\mathcal {P}}_{i}}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =\oint \mathbf {E} \cdot \mathrm {d} \mathbf {l} =0$ ${\textstyle {\mathcal {P}}_{i}}$

Tenga en cuenta que esta derivación utiliza la siguiente definición para el aumento de voltaje de a : $a$ $b$ $V_{a\to b}=-\int _{{\mathcal {P}}_{a\to b}}\mathbf {E} \cdot \mathrm {d} \mathbf {l}$

Sin embargo, el potencial eléctrico (y por lo tanto el voltaje) se puede definir de otras maneras, como por ejemplo mediante la descomposición de Helmholtz .

Generalización

En el límite de baja frecuencia, la caída de tensión alrededor de cualquier bucle es cero. Esto incluye bucles imaginarios dispuestos arbitrariamente en el espacio, no limitados a los bucles delineados por los elementos y conductores del circuito. En el límite de baja frecuencia, este es un corolario de la ley de inducción de Faraday (que es una de las ecuaciones de Maxwell ).

Esto tiene una aplicación práctica en situaciones que involucran " electricidad estática ".

Limitaciones

Las leyes de circuitos de Kirchhoff son el resultado del modelo de elementos concentrados y ambas dependen de que el modelo sea aplicable al circuito en cuestión. Cuando el modelo no es aplicable, las leyes no se aplican.

La ley actual depende del supuesto de que la carga neta en cualquier cable, unión o componente concentrado es constante. Siempre que el campo eléctrico entre las partes del circuito no sea despreciable, como cuando dos cables están acoplados capacitivamente , este puede no ser el caso. Esto ocurre en circuitos de CA de alta frecuencia, donde el modelo de elementos concentrados ya no es aplicable. ^[4] Por ejemplo, en una línea de transmisión , la densidad de carga en el conductor puede cambiar constantemente.

En una línea de transmisión, la carga neta en diferentes partes del conductor cambia con el tiempo. En el sentido físico directo, esto viola la LCK.

Por otra parte, la ley de voltaje se basa en el hecho de que las acciones de los campos magnéticos que varían con el tiempo están confinadas a componentes individuales, como los inductores. En realidad, el campo eléctrico inducido producido por un inductor no está confinado, pero los campos de fuga suelen ser insignificantes.

Modelado de circuitos reales con elementos concentrados

La aproximación de elementos concentrados para un circuito es precisa a bajas frecuencias. A frecuencias más altas, los flujos de fuga y las densidades de carga variables en los conductores se vuelven significativos. Hasta cierto punto, todavía es posible modelar dichos circuitos utilizando componentes parásitos . Si las frecuencias son demasiado altas, puede ser más apropiado simular los campos directamente utilizando el modelado de elementos finitos u otras técnicas .

Para modelar circuitos de modo que ambas leyes puedan seguir utilizándose, es importante entender la distinción entre los elementos físicos del circuito y los elementos agrupados ideales . Por ejemplo, un cable no es un conductor ideal. A diferencia de un conductor ideal, los cables pueden acoplarse inductiva y capacitivamente entre sí (y consigo mismos), y tienen un retardo de propagación finito. Los conductores reales pueden modelarse en términos de elementos agrupados considerando capacitancias parásitas distribuidas entre los conductores para modelar el acoplamiento capacitivo, o inductancias parásitas (mutuas) para modelar el acoplamiento inductivo. ^[4] Los cables también tienen cierta autoinductancia.

Ejemplo

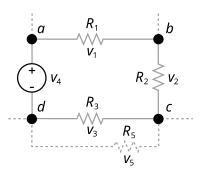
Supongamos una red eléctrica que consta de dos fuentes de tensión y tres resistencias.

Según la primera ley: Aplicando la segunda ley al circuito cerrado $s$ $1$ y sustituyendo el voltaje utilizando la ley de Ohm se obtiene: La segunda ley, nuevamente combinada con la ley de Ohm, aplicada al circuito cerrado $s$ $2$ da: $i_{1}-i_{2}-i_{3}=0$ $-R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}=0$ $-R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}=0$

Esto produce un sistema de ecuaciones lineales en $i 1$ , $i 2$ , $i 3$ : que es equivalente a Suponer que la solución es ${\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}&=0\end{cases}}$ ${\begin{cases}i_{1}+(-i_{2})+(-i_{3})&=0\\R_{1}i_{1}+R_{2}i_{2}+0i_{3}&={\mathcal {E}}_{1}\\0i_{1}+R_{2}i_{2}-R_{3}i_{3}&={\mathcal {E}}_{1}+{\mathcal {E}}_{2}\end{cases}}$ ${\begin{aligned}R_{1}&=100\Omega ,&R_{2}&=200\Omega ,&R_{3}&=300\Omega ,\\{\mathcal {E}}_{1}&=3{\text{V}},&{\mathcal {E}}_{2}&=4{\text{V}}\end{aligned}}$ ${\begin{cases}i_{1}={\frac {1}{1100}}{\text{A}}\\[6pt]i_{2}={\frac {4}{275}}{\text{A}}\\[6pt]i_{3}=-{\frac {3}{220}}{\text{A}}\end{cases}}$

La corriente $i 3$ tiene un signo negativo, lo que significa que la dirección supuesta de $i 3$ era incorrecta y que $i 3$ en realidad fluye en la dirección opuesta a la flecha roja etiquetada $i 3$ . La corriente en $R 3$ fluye de izquierda a derecha.

Véase también

Referencias

^ Oldham, Kalil T. Swain (2008). La doctrina de la descripción: Gustav Kirchhoff, la física clásica y el "propósito de toda ciencia" en la Alemania del siglo XIX (Ph. D.). Universidad de California, Berkeley. p. 52. Expediente 3331743.
^ Athavale, Prashant. "Ley de corriente de Kirchoff y ley de voltaje de Kirchoff" (PDF) . Universidad Johns Hopkins . Consultado el 6 de diciembre de 2018 .
^ ab "Las conferencias Feynman sobre física, vol. II, cap. 22: circuitos de corriente alterna". feynmanlectures.caltech.edu . Consultado el 6 de diciembre de 2018 .
^ de Ralph Morrison, Técnicas de puesta a tierra y blindaje en instrumentación Wiley-Interscience (1986) ISBN 0471838055

Paul, Clayton R. (2001). Fundamentos del análisis de circuitos eléctricos . John Wiley & Sons. ISBN 0-471-37195-5.
Serway, Raymond A.; Jewett, John W. (2004). Física para científicos e ingenieros (6.ª ed.) . Brooks/Cole. ISBN 0-534-40842-7.
Tipler, Paul (2004). Física para científicos e ingenieros: electricidad, magnetismo, luz y física moderna elemental (5.ª ed.) . WH Freeman. ISBN 0-7167-0810-8.
Graham, Howard Johnson, Martin (2002). Propagación de señales a alta velocidad: magia negra avanzada (10.ª edición). Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-084408-X.{{cite book}}: CS1 maint: multiple names: authors list (link)

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Leyes de circuitos de Kirchhoff .

Capítulo Circuitos divisores y leyes de Kirchhoff de Lecciones de circuitos eléctricos, vol. 1, libro electrónico gratuito de CC y de la serie Lecciones de circuitos eléctricos