En ciencia, un proceso que no es reversible se llama irreversible . Este concepto surge con frecuencia en termodinámica . Todos los procesos naturales complejos son irreversibles, [1] [2] [3] [4] aunque una transición de fase a la temperatura de coexistencia (por ejemplo, la fusión de cubitos de hielo en agua) se aproxima bien como reversible.
En termodinámica, un cambio en el estado termodinámico de un sistema y todo su entorno no puede restaurarse con precisión a su estado inicial mediante cambios infinitesimales en alguna propiedad del sistema sin gasto de energía. Un sistema que experimenta un proceso irreversible aún puede ser capaz de regresar a su estado inicial. Debido a que la entropía es una función de estado , el cambio en la entropía del sistema es el mismo independientemente de que el proceso sea reversible o irreversible. Sin embargo, ocurre la imposibilidad de restaurar el entorno a sus propias condiciones iniciales. Un proceso irreversible aumenta la entropía total del sistema y su entorno. La segunda ley de la termodinámica se puede utilizar para determinar si un proceso hipotético es reversible o no.
Intuitivamente, un proceso es reversible si no hay disipación . Por ejemplo, la expansión de Joule es irreversible porque inicialmente el sistema no es uniforme. Inicialmente, hay una parte del sistema con gas y otra parte sin gas. Para que se produzca la disipación, es necesario que exista dicha falta de uniformidad. Esto es lo mismo que si en un sistema una sección del gas estuviera caliente y la otra fría. Entonces se produciría la disipación; la distribución de la temperatura se volvería uniforme sin que se realizara trabajo, y esto sería irreversible porque no se podría añadir o quitar calor ni cambiar el volumen para devolver el sistema a su estado inicial. Por tanto, si el sistema es siempre uniforme, entonces el proceso es reversible, lo que significa que se puede devolver el sistema a su estado original añadiendo o quitando calor, realizando trabajo en el sistema o dejando que el sistema realice trabajo. Como otro ejemplo, para aproximar la expansión en un motor de combustión interna como reversible, supondríamos que la temperatura y la presión cambian uniformemente en todo el volumen después de la chispa. Obviamente, esto no es cierto y se produce un frente de llama y, a veces, incluso golpeteo del motor . Una de las razones por las que los motores diésel pueden lograr una mayor eficiencia es que la combustión es mucho más uniforme, por lo que se pierde menos energía por disipación y el proceso es más cercano a ser reversible. [ cita requerida ]
El fenómeno de la irreversibilidad resulta del hecho de que si un sistema termodinámico , que es cualquier sistema de suficiente complejidad, de moléculas interactuantes se lleva de un estado termodinámico a otro, la configuración o disposición de los átomos y moléculas en el sistema cambiará de una manera que no es fácilmente predecible. [5] [6] Se utilizará cierta "energía de transformación" ya que las moléculas del "cuerpo de trabajo" realizan trabajo entre sí cuando cambian de un estado a otro. Durante esta transformación, habrá cierta pérdida o disipación de energía térmica debido a la fricción y las colisiones intermoleculares. Esta energía no será recuperable si el proceso se invierte.
Se ha descubierto que muchos procesos biológicos que antes se creían reversibles son en realidad una combinación de dos procesos irreversibles. Mientras que antes se creía que una sola enzima catalizaba tanto los cambios químicos directos como los inversos, las investigaciones han descubierto que normalmente se necesitan dos enzimas separadas de estructura similar para llevar a cabo lo que da como resultado un par de procesos termodinámicamente irreversibles. [7]
La termodinámica define el comportamiento estadístico de un gran número de entidades, cuyo comportamiento exacto está dado por leyes más específicas. Si bien las leyes teóricas fundamentales de la física son todas reversibles en el tiempo, [8] experimentalmente la probabilidad de reversibilidad real es baja y el estado anterior del sistema y sus alrededores se recupera solo en cierta medida (ver: principio de incertidumbre ). La reversibilidad de la termodinámica debe ser de naturaleza estadística; es decir, debe ser meramente altamente improbable, pero no imposible, que un sistema disminuya su entropía. En otras palabras, la reversibilidad temporal se cumple si el proceso sucede de la misma manera si el tiempo fluyera en sentido inverso o si se invirtiera el orden de estados en el proceso (el último estado se convierte en el primero y viceversa).
El físico alemán Rudolf Clausius , en la década de 1850, fue el primero en cuantificar matemáticamente el descubrimiento de la irreversibilidad en la naturaleza mediante la introducción del concepto de entropía . En sus memorias de 1854 "Sobre una forma modificada del segundo teorema fundamental en la teoría mecánica del calor", Clausius afirma:
Puede, además, suceder que en lugar de una transmisión descendente de calor que acompaña, en el mismo proceso, a la transmisión ascendente, se produzca otro cambio permanente que tenga la particularidad de no ser reversible sin ser reemplazado por un nuevo cambio permanente de tipo similar o sin producir una transmisión descendente de calor.
En términos simples, Clausius afirma que es imposible que un sistema transfiera calor de un cuerpo más frío a un cuerpo más caliente. Por ejemplo, una taza de café caliente colocada en un área a temperatura ambiente (~72 °F) transferirá calor a sus alrededores y, por lo tanto, se enfriará a medida que la temperatura de la habitación aumente ligeramente (a ~72,3 °F ). Sin embargo, esa misma taza de café inicial nunca absorberá calor de sus alrededores, lo que hará que se caliente aún más, a medida que la temperatura de la habitación disminuya (a ~71,7 °F ). Por lo tanto, el proceso de enfriamiento del café es irreversible a menos que se agregue energía adicional al sistema.
Sin embargo, surgió una paradoja al intentar reconciliar el microanálisis de un sistema con las observaciones de su macroestado. Muchos procesos son matemáticamente reversibles en su microestado cuando se analizan utilizando la mecánica newtoniana clásica. Esta paradoja claramente contamina las explicaciones microscópicas de la tendencia macroscópica hacia el equilibrio, como el argumento de James Clerk Maxwell de 1860 de que las colisiones moleculares implican una igualación de las temperaturas de los gases mezclados. [9] De 1872 a 1875, Ludwig Boltzmann reforzó la explicación estadística de esta paradoja en forma de la fórmula de entropía de Boltzmann , afirmando que un aumento del número de posibles microestados en los que podría estar un sistema, aumentará la entropía del sistema, haciendo menos probable que el sistema regrese a un estado anterior. Sus fórmulas cuantificaron el análisis realizado por William Thomson, primer barón Kelvin , quien había argumentado que: [10] [11]
Las ecuaciones de movimiento en dinámica abstracta son perfectamente reversibles; cualquier solución de estas ecuaciones sigue siendo válida cuando la variable temporal t se sustituye por –t. Por otra parte, los procesos físicos son irreversibles: por ejemplo, la fricción de los sólidos, la conducción del calor y la difusión. Sin embargo, el principio de disipación de energía es compatible con una teoría molecular en la que cada partícula está sujeta a las leyes de la dinámica abstracta.
Otra explicación de los sistemas irreversibles fue presentada por el matemático francés Henri Poincaré . En 1890, publicó su primera explicación de la dinámica no lineal, también llamada teoría del caos . Aplicando la teoría del caos a la segunda ley de la termodinámica , la paradoja de la irreversibilidad puede explicarse en los errores asociados con el escalamiento de microestados a macroestados y los grados de libertad utilizados al hacer observaciones experimentales. La sensibilidad a las condiciones iniciales relacionadas con el sistema y su entorno en los microestados se combina con una exhibición de características irreversibles dentro del ámbito físico observable. [12]
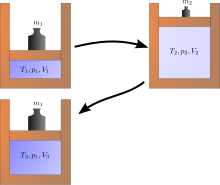
En el ámbito físico existen numerosos procesos irreversibles a los que se puede atribuir la incapacidad de alcanzar una eficiencia del 100% en la transferencia de energía. A continuación se enumeran algunos eventos espontáneos que contribuyen a la irreversibilidad de los procesos. [13]
Una expansión de Joule es un ejemplo de termodinámica clásica, ya que es fácil calcular el aumento de entropía resultante. Ocurre cuando un volumen de gas se mantiene en un lado de un recipiente aislado térmicamente (a través de una pequeña partición), mientras que el otro lado del recipiente se vacía; luego, la partición entre las dos partes del recipiente se abre y el gas llena todo el recipiente. La energía interna del gas permanece igual, mientras que el volumen aumenta. El estado original no se puede recuperar simplemente comprimiendo el gas a su volumen original, ya que la energía interna aumentará por esta compresión. El estado original solo se puede recuperar enfriando luego el sistema recomprimido y, por lo tanto, calentando irreversiblemente el entorno. El diagrama de la derecha se aplica solo si la primera expansión es "libre" (expansión de Joule), es decir, no puede haber presión atmosférica fuera del cilindro y no se levanta ningún peso.
La diferencia entre eventos reversibles e irreversibles tiene un valor explicativo particular en sistemas complejos (como organismos vivos o ecosistemas ). Según los biólogos Humberto Maturana y Francisco Varela , los organismos vivos se caracterizan por la autopoiesis , que permite su existencia continua. El físico y químico Ilya Prigogine ha descrito formas más primitivas de sistemas autoorganizados . En el contexto de los sistemas complejos, los eventos que conducen al final de ciertos procesos autoorganizativos , como la muerte , la extinción de una especie o el colapso de un sistema meteorológico, pueden considerarse irreversibles. Incluso si se pudiera desarrollar un clon con el mismo principio organizativo (por ejemplo, una estructura de ADN idéntica), esto no significaría que el sistema anterior distinto volviera a existir. Los eventos a los que las capacidades autoorganizativas de los organismos, especies u otros sistemas complejos pueden adaptarse, como lesiones menores o cambios en el entorno físico, son reversibles. Sin embargo, la adaptación depende de la importación de negentropía en el organismo, lo que aumenta los procesos irreversibles en su entorno. [17] Los principios ecológicos, como los de sostenibilidad y el principio de precaución, pueden definirse con referencia al concepto de reversibilidad. [18] [19] [20] [21] [22] [23] [5] [24] [25]