Flujo no viscoso

Flujo de fluidos con viscosidad cero (superfluidos)

En dinámica de fluidos , el flujo no viscoso es el flujo de un fluido no viscoso , que es un fluido con viscosidad cero . ^[1]

El número de Reynolds del flujo no viscoso se acerca al infinito a medida que la viscosidad se acerca a cero. Cuando se desprecian las fuerzas viscosas, como en el caso del flujo no viscoso, la ecuación de Navier-Stokes se puede simplificar a una forma conocida como ecuación de Euler . Esta ecuación simplificada es aplicable al flujo no viscoso, así como al flujo con baja viscosidad y un número de Reynolds mucho mayor que uno. Utilizando la ecuación de Euler, muchos problemas de dinámica de fluidos que involucran baja viscosidad se resuelven fácilmente; sin embargo, la supuesta viscosidad despreciable ya no es válida en la región del fluido cerca de un límite sólido (la capa límite ) o, de manera más general, en regiones con grandes gradientes de velocidad que evidentemente están acompañados por fuerzas viscosas. ^{[1] [2] [3]}

El flujo de un superfluido no es viscoso. ^[4]

Los flujos no viscosos se clasifican en general en flujos potenciales (o flujos irrotacionales) y flujos no viscosos rotacionales.

Hipótesis de Prandtl

Estos diagramas muestran las líneas de corriente divisorias asociadas con un perfil aerodinámico en un flujo no viscoso bidimensional.
El diagrama superior muestra circulación cero y sustentación cero. Implica un flujo de vórtice de alta velocidad en el borde de salida, lo que se sabe que es inexacto en un modelo de estado estable.
El diagrama inferior muestra la condición de Kutta, que implica circulación finita, sustentación finita y ausencia de flujo de vórtice en el borde de salida. Se sabe que estas características son precisas como modelos de estado estable en un fluido real.

Ludwig Prandtl desarrolló el concepto moderno de capa límite . Su hipótesis establece que para fluidos de baja viscosidad, las fuerzas de corte debidas a la viscosidad son evidentes solo en regiones delgadas en el límite del fluido, adyacentes a superficies sólidas. Fuera de estas regiones, y en regiones de gradiente de presión favorable, las fuerzas de corte viscosas están ausentes, por lo que se puede suponer que el campo de flujo del fluido es el mismo que el flujo de un fluido no viscoso. Al emplear la hipótesis de Prandtl, es posible estimar el flujo de un fluido real en regiones de gradiente de presión favorable asumiendo un flujo no viscoso e investigando el patrón de flujo irrotacional alrededor del cuerpo sólido. ^[5]

Los fluidos reales experimentan la separación de la capa límite y las estelas turbulentas resultantes, pero estos fenómenos no se pueden modelar utilizando flujo no viscoso. La separación de la capa límite generalmente ocurre cuando el gradiente de presión cambia de favorable a adverso, por lo que es inexacto utilizar el flujo no viscoso para estimar el flujo de un fluido real en regiones de gradiente de presión desfavorable . ^[5]

Número de Reynolds

El número de Reynolds (Re) es una cantidad adimensional que se utiliza comúnmente en dinámica de fluidos e ingeniería. ^{[6] [7]} Originalmente descrito por George Gabriel Stokes en 1850, se popularizó gracias a Osborne Reynolds, en cuyo honor Arnold Sommerfeld le dio el nombre al concepto en 1908. ^{[7] [8] [9]} El número de Reynolds se calcula como:

${\displaystyle Re={l_{c}v\rho \over \mu }}$

El valor representa la relación entre las fuerzas inerciales y las fuerzas viscosas en un fluido, y es útil para determinar la importancia relativa de la viscosidad. ^[6] En un flujo no viscoso, dado que las fuerzas viscosas son cero, el número de Reynolds se acerca al infinito. ^[1] Cuando las fuerzas viscosas son insignificantes, el número de Reynolds es mucho mayor que uno. ^[1] En tales casos (Re>>1), suponer un flujo no viscoso puede ser útil para simplificar muchos problemas de dinámica de fluidos.

Ecuaciones de Euler

Flujo no viscoso alrededor de un ala, suponiendo una circulación que alcance la condición de Kutta

En una publicación de 1757, Leonhard Euler describió un conjunto de ecuaciones que gobiernan el flujo no viscoso: ^[10]

${\displaystyle \rho {D\mathbf {v} \over Dt}=-\nabla p+\rho \mathbf {g} }$

Suponiendo que el flujo no es viscoso, la ecuación de Euler se puede aplicar a flujos en los que las fuerzas viscosas son insignificantes. ^[1] Algunos ejemplos incluyen el flujo alrededor del ala de un avión, el flujo ascendente alrededor de los soportes de un puente en un río y las corrientes oceánicas. ^[1]

Ecuaciones de Navier-Stokes

En 1845, George Gabriel Stokes publicó otro conjunto importante de ecuaciones, hoy conocidas como ecuaciones de Navier-Stokes . ^{[1] [11]} Claude-Louis Navier desarrolló las ecuaciones primero usando la teoría molecular, que fue confirmada posteriormente por Stokes usando la teoría del continuo. ^[1] Las ecuaciones de Navier-Stokes describen el movimiento de los fluidos: ^[1]

${\displaystyle \rho {D\mathbf {v} \over Dt}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {g} }$

Cuando el fluido no es viscoso, o se puede suponer que la viscosidad es insignificante, la ecuación de Navier-Stokes se simplifica a la ecuación de Euler: ^[1] Esta simplificación es mucho más fácil de resolver y se puede aplicar a muchos tipos de flujo en los que la viscosidad es insignificante. ^[1] Algunos ejemplos incluyen el flujo alrededor del ala de un avión, el flujo ascendente alrededor de los soportes de un puente en un río y las corrientes oceánicas. ^[1]

La ecuación de Navier-Stokes se reduce a la ecuación de Euler cuando . Otra condición que conduce a la eliminación de la fuerza viscosa es , y esto da como resultado una "disposición de flujo no viscoso". ^[12] Se ha descubierto que tales flujos son similares a vórtices. ${\displaystyle \mu =0}$ ${\displaystyle \nabla ^{2}\mathbf {v} =0}$

Flujo que se desarrolla sobre una superficie sólida

Límites sólidos

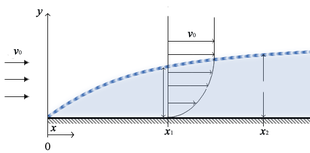
Es importante señalar que ya no se puede suponer que la viscosidad es despreciable cerca de los límites sólidos, como en el caso del ala de un avión. ^[1] En regímenes de flujo turbulento (Re >> 1), la viscosidad normalmente se puede despreciar, sin embargo, esto solo es válido a distancias alejadas de las interfaces sólidas. ^[1] Al considerar el flujo en las proximidades de una superficie sólida, como el flujo a través de una tubería o alrededor de un ala, es conveniente categorizar cuatro regiones distintas de flujo cerca de la superficie: ^[1]

• Corriente turbulenta principal: más alejada de la superficie, la viscosidad puede despreciarse.
• Subcapa inercial: El inicio de la corriente turbulenta principal, la viscosidad tiene una importancia menor.
• Capa amortiguadora: La transformación entre capas inerciales y viscosas.
• Subcapa viscosa : más cercana a la superficie, aquí la viscosidad es importante.

Aunque estas distinciones pueden ser una herramienta útil para ilustrar la importancia de las fuerzas viscosas cerca de las interfaces sólidas, es importante señalar que estas regiones son bastante arbitrarias. ^[1] Suponer que el flujo no viscoso puede ser una herramienta útil para resolver muchos problemas de dinámica de fluidos, sin embargo, esta suposición requiere una consideración cuidadosa de las subcapas del fluido cuando hay límites sólidos involucrados.

Superfluidos

Helio superfluido

El superfluido es el estado de la materia que exhibe flujo sin fricción, viscosidad cero, también conocido como flujo no viscoso. ^[4]

Hasta la fecha, el helio es el único fluido que se ha descubierto que exhibe superfluidez. El helio-4 se convierte en un superfluido una vez que se enfría por debajo de 2,2 K, un punto conocido como el punto lambda . ^[13] A temperaturas superiores al punto lambda, el helio existe como un líquido que exhibe un comportamiento fluidodinámico normal. Una vez que se enfría por debajo de 2,2 K, comienza a exhibir un comportamiento cuántico . Por ejemplo, en el punto lambda hay un aumento brusco de la capacidad térmica, a medida que continúa enfriándose, la capacidad térmica comienza a disminuir con la temperatura. ^[14] Además, la conductividad térmica es muy grande, lo que contribuye a las excelentes propiedades refrigerantes del helio superfluido. ^[15] De manera similar, el helio-3 se convierte en un superfluido a 2,491 mK.

Aplicaciones

Los espectrómetros se mantienen a una temperatura muy baja utilizando helio como refrigerante. Esto permite un flujo de fondo mínimo en las lecturas de infrarrojo lejano. Algunos de los diseños de los espectrómetros pueden ser simples, pero incluso el marco está en su punto más cálido a menos de 20 Kelvin. Estos dispositivos no se utilizan comúnmente ya que es muy caro utilizar helio superfluido en lugar de otros refrigerantes. ^[16]

Gran Colisionador de Hadrones

El helio superfluido tiene una conductividad térmica muy alta, lo que lo hace muy útil para enfriar superconductores. Los superconductores como los que se utilizan en el LHC (Gran Colisionador de Hadrones) se enfrían a temperaturas de aproximadamente 1,9 Kelvin. Esta temperatura permite que los imanes de niobio-titanio alcancen un estado superconductor. Sin el uso del helio superfluido, esta temperatura no sería posible. El uso de helio para enfriar a estas temperaturas es muy costoso y los sistemas de refrigeración que utilizan fluidos alternativos son cada vez más numerosos. ^[17]

Otra aplicación del helio superfluido es su uso para comprender la mecánica cuántica. El uso de láseres para observar pequeñas gotas permite a los científicos ver comportamientos que normalmente no serían visibles. Esto se debe a que todo el helio en cada gota se encuentra en el mismo estado cuántico. Esta aplicación no tiene ningún uso práctico en sí misma, pero nos ayuda a comprender mejor la mecánica cuántica, que tiene sus propias aplicaciones.

Véase también

• Flujo de Couette
• Dinámica de fluidos
• Flujo potencial , un caso especial de flujo no viscoso
• Flujo de Stokes , en el que las fuerzas viscosas son mucho mayores que las fuerzas inerciales.
• Viscosidad

Referencias

1. E., Stewart, Warren; N., Lightfoot, Edwin (1 de enero de 2007). Fenómenos de transporte . Wiley. ISBN 9780470115398.OCLC 762715172  .{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )
2. Clancy, LJ, Aerodinámica , pág. xviii
3. Kundu, PK, Cohen, IM y Hu, HH, Mecánica de fluidos , Capítulo 10, subcapítulo 1
4. S., Stringari (2016). Condensación de Bose-Einstein y superfluidez . Oxford University Press. ISBN 9780198758884.OCLC 936040211  .
5. Streeter, Victor L. (1966) Mecánica de fluidos , secciones 5.6 y 7.1, 4.ª edición, McGraw-Hill Book Co., Biblioteca del Congreso, número de catálogo 66-15605
6. L., Bergman, Theodore; S., Lavine, Adrienne ; P., Incropera, Frank; P., Dewitt, David (1 de enero de 2011). Fundamentos de transferencia de calor y masa . Wiley. ISBN 9780470501979.OCLC 875769912  .{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )
7. Rott, N (28 de noviembre de 2003). "Nota sobre la historia del número de Reynolds". Revista anual de mecánica de fluidos . 22 (1): 1–12. Código Bibliográfico :1990AnRFM..22....1R. doi :10.1146/annurev.fl.22.010190.000245.
8. Reynolds, Osborne (1 de enero de 1883). "Una investigación experimental de las circunstancias que determinan si el movimiento del agua será directo o sinuoso, y de la ley de resistencia en canales paralelos". Philosophical Transactions of the Royal Society of London . 174 : 935–982. Bibcode :1883RSPT..174..935R. doi : 10.1098/rstl.1883.0029 . ISSN  0261-0523.
9. Stokes, GG (1 de enero de 1851). "Sobre el efecto de la fricción interna de los fluidos en el movimiento de los péndulos". Transactions of the Cambridge Philosophical Society . 9 : 8. Bibcode :1851TCaPS...9....8S.
10. Euler, Leonhard (1757). ""Principes généraux de l'état d'équilibre d'un fluide "[Principios generales del estado de equilibrio]". Mémoires de l'académie des sciences de Berlin . 11 : 217–273.
11. Stokes, GG (1845). "Sobre las teorías de la fricción interna de fluidos en movimiento y del equilibrio y movimiento de sólidos elásticos". Proc. Camb. Phil. Soc . 8 : 287–319.
12. Runstedtler, Allan (2013). "Disposiciones de flujo no viscoso en dinámica de fluidos". Revista internacional de investigación en mecánica de fluidos . 40 (2): 148–158. doi :10.1615/interjfluidmechres.v40.i2.50. ISSN  1064-2277.
13. "Este mes en la historia de la física". www.aps.org . Consultado el 7 de marzo de 2017 .
14. Landau, L. (1941). "Teoría de la superfluidez del helio II". Physical Review . 60 (4): 356–358. Código Bibliográfico :1941PhRv...60..356L. doi :10.1103/physrev.60.356.
15. "Portal de la física de la naturaleza - Mirando hacia atrás - Siguiendo la corriente - Se observó superfluidez". www.nature.com . Consultado el 7 de marzo de 2017 .
16. HOUCK, JR; WARD, DENNIS (1 de enero de 1979). "Un espectrómetro de rejilla refrigerado por helio líquido para observaciones astronómicas en el infrarrojo lejano". Publicaciones de la Sociedad Astronómica del Pacífico . 91 (539): 140–142. Bibcode :1979PASP...91..140H. doi : 10.1086/130456 . JSTOR  40677459. S2CID  120273071.
17. "Criogenia: Bajas temperaturas, alto rendimiento | CERN". home.cern . Consultado el 14 de febrero de 2017 .