Restricciones holonómicas

Type of constraints for mechanical systems

En mecánica clásica , las restricciones holonómicas son relaciones entre las variables de posición (y posiblemente el tiempo) ^[1] que se pueden expresar de la siguiente forma:

${\displaystyle f(u_{1},u_{2},u_{3},\ldots ,u_{n},t)=0}$

donde están n coordenadas generalizadas que describen el sistema (en un espacio de configuración sin restricciones ). Por ejemplo, el movimiento de una partícula obligada a permanecer en la superficie de una esfera está sujeto a una restricción holonómica, pero si la partícula puede caerse de la esfera bajo la influencia de la gravedad, la restricción se vuelve no holonómica. Para el primer caso, la restricción holonómica puede venir dada por la ecuación ${\displaystyle \{u_{1},u_{2},u_{3},\ldots ,u_{n}\}}$

${\displaystyle r^{2}-a^{2}=0}$

donde es la distancia desde el centro de una esfera de radio , mientras que el segundo caso no holonómico puede venir dado por ${\displaystyle r}$ ${\displaystyle a}$

${\displaystyle r^{2}-a^{2}\geq 0}$

Restricciones dependientes de la velocidad (también llamadas restricciones semiholonómicas) ^[2] como

${\displaystyle f(u_{1},u_{2},\ldots ,u_{n},{\dot {u}}_{1},{\dot {u}}_{2},\ldots ,{\dot {u}}_{n},t)=0}$

No suelen ser holonómicos. ^{[ cita necesaria ]}

sistema holonómico

En la mecánica clásica, un sistema puede definirse como holonómico si todas las restricciones del sistema son holonómicas. Para que una restricción sea holonómica debe poder expresarse como una función :

${\displaystyle f(u_{1},\ u_{2},\ u_{3},\ \ldots ,\ u_{n},\ t)=0,\,}$

es decir, una restricción holonómica depende sólo de las coordenadas y tal vez del tiempo . ^[1] No depende de las velocidades ni de ninguna derivada de orden superior con respecto a  t . Una restricción que no se puede expresar en la forma mostrada arriba es una restricción no holonómica . ${\displaystyle u_{j}}$ ${\displaystyle t}$

Introducción

Como se describió anteriormente, un sistema holonómico es (simplemente hablando) un sistema en el que uno puede deducir el estado de un sistema conociendo sólo el cambio de posiciones de los componentes del sistema a lo largo del tiempo, pero no necesita saber la velocidad o en qué ordenar los componentes movidos entre sí. Por el contrario, un sistema no holonómico es a menudo un sistema en el que se deben conocer las velocidades de los componentes a lo largo del tiempo para poder determinar el cambio de estado del sistema, o un sistema en el que una parte móvil no puede estar sujeta a una restricción. superficie, real o imaginaria. Ejemplos de sistemas holonómicos son las grúas pórtico, los péndulos y los brazos robóticos. Ejemplos de sistemas no holonómicos son los Segways , los monociclos y los automóviles.

Terminología

El espacio de configuración enumera el desplazamiento de los componentes del sistema, uno para cada grado de libertad . Un sistema que puede describirse utilizando un espacio de configuración se llama escleronómico . ${\displaystyle {\overrightarrow {u}}}$

${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&\ldots &u_{n}\end{bmatrix}}^{\mathrm {T} }}$

El espacio de eventos es idéntico al espacio de configuración excepto por la adición de una variable para representar el cambio en el sistema a lo largo del tiempo (si es necesario para describir el sistema). Un sistema que debe describirse utilizando un espacio de eventos, en lugar de solo un espacio de configuración, se llama reonómico . Muchos sistemas pueden describirse de forma escleronómica o reonómica. Por ejemplo, el movimiento total permitido de un péndulo se puede describir con una restricción escleronómica, pero el movimiento a lo largo del tiempo de un péndulo se debe describir con una restricción reonómica. ${\displaystyle t}$

${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&\ldots &u_{n}&t\end{bmatrix}}^{\mathrm {T} }}$

El espacio de estados es el espacio de configuración, más los términos que describen la velocidad de cada término en el espacio de configuración. ${\displaystyle {\overrightarrow {q}}}$

${\displaystyle {\overrightarrow {q}}={\begin{bmatrix}{\overrightarrow {u}}\\{\overrightarrow {\dot {u}}}\end{bmatrix}}={\begin{bmatrix}u_{1}&\ldots &u_{n}&{\dot {u}}_{1}&\ldots &{\dot {u}}_{n}\end{bmatrix}}^{\mathrm {T} }}$

El espacio de tiempo-estado agrega tiempo . ${\displaystyle t}$

${\displaystyle {\overrightarrow {q}}={\begin{bmatrix}{\overrightarrow {u}}\\{\overrightarrow {\dot {u}}}\end{bmatrix}}={\begin{bmatrix}u_{1}&\ldots &u_{n}&t&{\dot {u}}_{1}&\ldots &{\dot {u}}_{n}\end{bmatrix}}^{\mathrm {T} }}$

Ejemplos

Grúa pórtico

Un gráfico de una grúa pórtico, con ejes marcados.

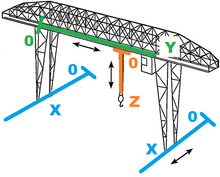
Como se muestra a la derecha, una grúa pórtico es un puente grúa que es capaz de mover su gancho en 3 ejes como indican las flechas. Intuitivamente, podemos deducir que la grúa debe ser un sistema holonómico ya que, para un movimiento dado de sus componentes, no importa en qué orden o velocidad se muevan los componentes: siempre que el desplazamiento total de cada componente desde una condición inicial dada es el mismo, todas las partes y el sistema en su conjunto terminarán en el mismo estado. Matemáticamente podemos demostrar esto como tal:

Podemos definir el espacio de configuración del sistema como:

${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}x\\y\\z\end{bmatrix}}}$

Podemos decir que las deflexiones de cada componente de la grúa desde su posición "cero" son , y , para los componentes azul, verde y naranja, respectivamente. La orientación y ubicación del sistema de coordenadas no importa si un sistema es holonómico, pero en este ejemplo los componentes se mueven paralelos a sus ejes. Si el origen del sistema de coordenadas está en la parte posterior inferior izquierda de la grúa, entonces podemos escribir la ecuación de restricción de posición como: ${\displaystyle B}$ ${\displaystyle G}$ ${\displaystyle O}$

${\displaystyle (x-B)+(y-G)+(z-(h-O))=0}$

¿ Dónde está la altura de la grúa? Opcionalmente, podemos simplificar a la forma estándar donde todas las constantes se colocan después de las variables: ${\displaystyle h}$

${\displaystyle x+y+z-(B+G+h-O)=0}$

Debido a que hemos derivado una ecuación de restricción en forma holonómica (específicamente, nuestra ecuación de restricción tiene la forma donde ), podemos ver que este sistema debe ser holonómico. ${\displaystyle f(x,y,z)=0}$ ${\displaystyle \{x,y,z\}\in {\overrightarrow {u}}}$

Péndulo

Un péndulo sencillo

Como se muestra a la derecha, un péndulo simple es un sistema compuesto por una pesa y una cuerda. La cuerda está unida en el extremo superior a un pivote y en el extremo inferior a un peso. Al ser inextensible, la longitud de la cuerda es constante. Este sistema es holonómico porque obedece a la restricción holonómica.

${\displaystyle {x^{2}+y^{2}}-L^{2}=0,}$

donde es la posición del peso y la longitud de la cuerda. ${\displaystyle (x,\ y)}$ ${\displaystyle L}$

Cuerpo rígido

Las partículas de un cuerpo rígido obedecen a la restricción holonómica.

${\displaystyle (\mathbf {r} _{i}-\mathbf {r} _{j})^{2}-L_{ij}^{2}=0,\,}$

donde , son respectivamente las posiciones de las partículas y , y es la distancia entre ellas. Si un sistema dado es holonómico, unir rígidamente partes adicionales a los componentes del sistema en cuestión no puede convertirlo en no holonómico, asumiendo que los grados de libertad no se reducen (en otras palabras, asumiendo que el espacio de configuración no cambia). ${\displaystyle \mathbf {r} _{i}}$ ${\displaystyle \mathbf {r} _{j}}$ ${\displaystyle P_{i}}$ ${\displaystyle P_{j}}$ ${\displaystyle L_{ij}}$

forma pfaffiana

Considere la siguiente forma diferencial de una restricción:

${\displaystyle \sum _{j}\ A_{ij}\,du_{j}+A_{i}\,dt=0}$

¿Dónde están los coeficientes de los diferenciales para la i -ésima ecuación de restricción? Esta forma se llama forma pfaffiana o forma diferencial . ${\displaystyle A_{ij},A_{i}}$ ${\displaystyle du_{j},dt}$

Si la forma diferencial es integrable, es decir, si existe una función que satisface la igualdad ${\displaystyle f_{i}(u_{1},\ u_{2},\ u_{3},\ \ldots ,\ u_{n},\ t)=0}$

${\displaystyle df_{i}=\sum _{j}\ A_{ij}\,du_{j}+A_{i}\,dt=0}$

entonces esta restricción es una restricción holonómica; de lo contrario, no es holonómico. Por lo tanto, todas las restricciones holonómicas y algunas no holonómicas se pueden expresar utilizando la forma diferencial. Ejemplos de restricciones no holonómicas que no pueden expresarse de esta manera son aquellas que dependen de velocidades generalizadas. ^{[ se necesita aclaración ]} Con una ecuación de restricción en forma pfaffiana, si la restricción es holonómica o no holonómica depende de si la forma pfaffiana es integrable. Consulte la Prueba universal para restricciones holonómicas a continuación para obtener una descripción de una prueba para verificar la integrabilidad (o la falta de) de una restricción de forma pfaffiana.

Prueba universal para restricciones holonómicas.

Cuando la ecuación de restricción de un sistema se escribe en forma de restricción de Pfaff , existe una prueba matemática para determinar si el sistema es holonómico.

Para una ecuación de restricción, o conjuntos de ecuaciones de restricción (tenga en cuenta que se pueden incluir variables que representan el tiempo, como se indicó anteriormente y en la siguiente forma): ${\displaystyle i}$ ${\displaystyle A_{i}\in A_{ij}}$ ${\displaystyle \,dt\in du_{j}}$

${\displaystyle \sum _{j}^{n}\ A_{ij}\,du_{j}=0;\,}$

podemos usar la ecuación de prueba:

${\displaystyle A_{\gamma }\left({\frac {\partial A_{\beta }}{\partial u_{\alpha }}}-{\frac {\partial A_{\alpha }}{\partial u_{\beta }}}\right)+A_{\beta }\left({\frac {\partial A_{\alpha }}{\partial u_{\gamma }}}-{\frac {\partial A_{\gamma }}{\partial u_{\alpha }}}\right)+A_{\alpha }\left({\frac {\partial A_{\gamma }}{\partial u_{\beta }}}-{\frac {\partial A_{\beta }}{\partial u_{\gamma }}}\right)=0}$

dónde

$${\displaystyle \alpha ,\beta ,\gamma =1,2,3\ldots n}$$

${\textstyle {\binom {n}{3}}={\frac {n(n-1)(n-2)}{6}}}$ ${\displaystyle i}$

En otras palabras, un sistema de tres variables tendría que probarse una vez con una ecuación de prueba cuyos términos sean términos de la ecuación de restricción (en cualquier orden), pero para probar un sistema de cuatro variables la prueba tendría que realizarse hasta a cuatro veces con cuatro ecuaciones de prueba diferentes, siendo los términos términos ,  ,  y en la ecuación de restricción (cada uno en cualquier orden) en cuatro pruebas diferentes. Para un sistema de cinco variables, se tendrían que realizar diez pruebas en un sistema holonómico para verificar ese hecho, y para un sistema de cinco variables con tres conjuntos de ecuaciones de restricción, treinta pruebas (asumiendo una simplificación como un cambio de variable). no se pudo realizar para reducir ese número). Por esta razón, es aconsejable, cuando se utiliza este método en sistemas de más de tres variables, usar el sentido común para determinar si el sistema en cuestión es holonómico y solo realizar pruebas si es probable que el sistema no lo sea. Además, también es mejor utilizar la intuición matemática para intentar predecir qué prueba fallará primero y comenzar con esa, saltándose al principio las pruebas que parecen tener éxito. ${\displaystyle \alpha ,\beta ,\gamma }$ ${\displaystyle 1,2,3}$ ${\displaystyle \alpha ,\beta ,\gamma }$ ${\displaystyle 1,2,3}$ ${\displaystyle 1,2,4}$ ${\displaystyle 1,3,4}$ ${\displaystyle 2,3,4}$

Si cada ecuación de prueba es verdadera para todo el conjunto de combinaciones de todas las ecuaciones de restricción, el sistema es holonómico. Si es falso incluso para una combinación de pruebas, el sistema no es holonómico.

Ejemplo

Considere este sistema dinámico descrito por una ecuación de restricción en forma de Pfaff.

${\displaystyle (\cos \theta )dx+(\sin \theta )dy+(y\cos \theta -x\sin \theta )d\theta =0}$

El espacio de configuración, por inspección, es . Debido a que sólo hay tres términos en el espacio de configuración, sólo se necesitará una ecuación de prueba. Podemos organizar los términos de la ecuación de restricción como tal, en preparación para la sustitución: ${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}x&y&\theta \end{bmatrix}}^{\mathrm {T} }}$

${\displaystyle A_{\alpha }=\cos \theta }$

${\displaystyle A_{\beta }=\sin \theta }$

${\displaystyle A_{\gamma }=y\cos \theta -x\sin \theta }$

${\displaystyle u_{\alpha }=dx}$

${\displaystyle u_{\beta }=dy}$

${\displaystyle u_{\gamma }=d\theta }$

Sustituyendo los términos, nuestra ecuación de prueba queda:

${\displaystyle (y\cos \theta -x\sin \theta ){\bigg (}{\frac {\partial }{\partial x}}(\sin \theta )-{\frac {\partial }{\partial y}}(\cos \theta ){\bigg )}+(\sin \theta ){\bigg (}{\frac {\partial }{\partial \theta }}(\cos \theta )-{\frac {\partial }{\partial x}}(y\cos \theta -x\sin \theta ){\bigg )}+(\cos \theta ){\bigg (}{\frac {\partial }{\partial y}}(y\cos \theta -x\sin \theta )-{\frac {\partial }{\partial \theta }}(\sin \theta ){\bigg )}=0}$

Después de calcular todas las derivadas parciales, obtenemos:

${\displaystyle (y\cos \theta -x\sin \theta ){\bigg (}0-0{\bigg )}+(\sin \theta ){\bigg (}-\sin \theta -(-\sin \theta ){\bigg )}+(\cos \theta ){\bigg (}\cos \theta -\cos \theta {\bigg )}=0}$

Simplificando encontramos que:

${\displaystyle 0=0}$

Vemos que nuestra ecuación de prueba es verdadera y, por tanto, el sistema debe ser holonómico.

Hemos terminado nuestra prueba, pero ahora que sabemos que el sistema es holonómico, es posible que deseemos encontrar la ecuación de restricción holonómica. Podemos intentar encontrarlo integrando cada término de la forma pfaffiana e intentando unificarlos en una ecuación, como tal:

${\displaystyle \int (\cos \theta )dx=x\cos \theta +f(y,\theta )}$

${\displaystyle \int (\sin \theta )dy=y\sin \theta +f(x,\theta )}$

${\displaystyle \int (y\cos \theta -x\sin \theta )d\theta =y\sin \theta +x\cos \theta +f(x,y)}$

Es fácil ver que podemos combinar los resultados de nuestras integraciones para encontrar la ecuación de restricción holonómica:

${\displaystyle y\sin \theta +x\cos \theta +C=0}$

donde C es la constante de integración.

Restricciones de coeficientes constantes.

Para una restricción de Pfaff dada donde cada coeficiente de cada diferencial es una constante, en otras palabras, una restricción de la forma:

${\displaystyle \sum _{j}\ A_{ij}\,du_{j}+A_{i}\,dt=0;\;\{A_{ij},A_{i};\,j=1,2,\ldots ;\,i=1,2,\ldots \}\in \mathbb {R} }$

la restricción debe ser holonómica.

Podemos probar esto de la siguiente manera: considere un sistema de restricciones en forma pfaffiana donde cada coeficiente de cada diferencial es una constante, como se describió directamente arriba. Para comprobar si este sistema de restricciones es holonómico, utilizamos la prueba universal. Podemos ver que en la ecuación de prueba, hay tres términos que deben sumar cero. Por lo tanto, si cada uno de esos tres términos en cada ecuación de prueba posible es cero, entonces todas las ecuaciones de prueba son verdaderas y el sistema es holonómico. Cada término de cada ecuación de prueba tiene la forma:

${\displaystyle A_{3}\left({\frac {\partial A_{2}}{\partial u_{1}}}-{\frac {\partial A_{1}}{\partial u_{2}}}\right)}$

dónde:

• ${\displaystyle A_{1}}$, y son alguna combinación (con combinaciones totales) de y para una restricción determinada . ${\displaystyle A_{2}}$ ${\displaystyle A_{3}}$ ${\textstyle {\binom {n}{3}}=n(n-1)(n-2)/6}$ ${\displaystyle A_{ij};\,j=1,2,\ldots }$ ${\displaystyle A_{i}}$ ${\displaystyle i}$
• ${\displaystyle u_{1}}$, y son la combinación correspondiente de y . ${\displaystyle u_{2}}$ ${\displaystyle u_{3}}$ ${\displaystyle u_{j};\,j=1,2,\ldots }$ ${\displaystyle dt}$

Además, existen conjuntos de ecuaciones de prueba. ${\displaystyle i}$

Podemos ver que, por definición, todos son constantes. Es bien sabido en cálculo que cualquier derivada (total o parcial) de cualquier constante es . Por tanto, podemos reducir cada derivada parcial a: ${\displaystyle A_{n}}$ ${\displaystyle 0}$

${\displaystyle A_{3}{\big (}0-0{\big )}}$

y por tanto cada término es cero, el lado izquierdo de cada ecuación de prueba es cero, cada ecuación de prueba es verdadera y el sistema es holonómico.

Espacios de configuración de dos o una variable

Cualquier sistema que pueda describirse mediante una restricción de Pfaff y tenga un espacio de configuración o espacio de estados de solo dos variables o una variable es holonómico.

Podemos probar esto como tal: considere un sistema dinámico con un espacio de configuración o espacio de estados descrito como:

${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}\end{bmatrix}}^{\mathrm {T} }}$

Si el sistema se describe mediante un espacio de estados, simplemente decimos que es igual a nuestra variable tiempo . Este sistema se describirá en forma pfaffiana: ${\displaystyle u_{2}}$ ${\displaystyle t}$

${\displaystyle A_{i1}du_{1}+A_{i2}du_{2}=0}$

con conjuntos de restricciones. El sistema se probará mediante el uso de la prueba universal. Sin embargo, la prueba universal requiere tres variables en la configuración o espacio de estados. Para acomodar esto, simplemente agregamos una variable ficticia a la configuración o espacio de estado para formar: ${\displaystyle i}$ ${\displaystyle \lambda }$

${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&\lambda \end{bmatrix}}^{\mathrm {T} }}$

Debido a que la variable ficticia , por definición, no es una medida de nada en el sistema, su coeficiente en la forma pfaffiana debe ser . Así revisamos nuestra forma Pfaffiana: ${\displaystyle \lambda }$ ${\displaystyle 0}$

${\displaystyle A_{i1}du_{1}+A_{i2}du_{2}+0d\lambda =0}$

Ahora podemos usar la prueba como tal, para una restricción dada si hay un conjunto de restricciones: ${\displaystyle i}$

${\displaystyle (0){\bigg (}{\frac {\partial }{\partial u_{1}}}(A_{i2})-{\frac {\partial }{\partial u_{2}}}(A_{i1}){\bigg )}+(A_{i2}){\bigg (}{\frac {\partial }{\partial \lambda }}(A_{i1})-{\frac {\partial }{\partial u_{1}}}(0){\bigg )}+(A_{i1}){\bigg (}{\frac {\partial }{\partial u_{2}}}(0)-{\frac {\partial }{\partial \lambda }}(A_{i2}){\bigg )}=0}$

Al darnos cuenta de que: debido a que la variable ficticia no puede aparecer en los coeficientes utilizados para describir el sistema, vemos que la ecuación de prueba debe ser verdadera para todos los conjuntos de ecuaciones de restricción y, por tanto, el sistema debe ser holonómico. Se puede realizar una prueba similar con una variable real en la configuración o espacio de estados y dos variables ficticias para confirmar que los sistemas de un grado de libertad describibles en forma pfaffiana también son siempre holonómicos. ${\displaystyle {\frac {\partial }{\partial \lambda }}(f(u_{1},u_{2}))=0}$ ${\displaystyle \lambda }$

En conclusión, nos damos cuenta de que aunque es posible modelar sistemas no holonómicos en forma pfaffiana, cualquier sistema modelable en forma pfaffiana con dos o menos grados de libertad (el número de grados de libertad es igual al número de términos en el espacio de configuración ) debe ser holonómico.

Nota importante: tenga en cuenta que la ecuación de prueba falló porque la variable ficticia, y por lo tanto el diferencial ficticio incluido en la prueba, diferenciará cualquier cosa que sea función de la configuración real o de las variables del espacio de estados . Tener un sistema con una configuración o espacio de estados de: ${\displaystyle 0}$

${\displaystyle {\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&u_{3}\end{bmatrix}}^{\mathrm {T} }}$

y un conjunto de restricciones donde una o más restricciones están en forma pfaffiana:

${\displaystyle A_{i1}du_{1}+A_{i2}du_{2}+0du_{3}=0}$

no garantiza que el sistema sea holonómico, ya que aunque un diferencial tenga un coeficiente de , todavía hay tres grados de libertad descritos en la configuración o espacio de estados . ${\displaystyle 0}$

Transformación a coordenadas generalizadas independientes.

Las ecuaciones de restricción holonómica pueden ayudarnos a eliminar fácilmente algunas de las variables dependientes de nuestro sistema. Por ejemplo, si queremos eliminar , que es un parámetro en la ecuación de restricción , podemos reorganizar la ecuación de la siguiente forma, asumiendo que se puede hacer: ${\displaystyle x_{d}}$ ${\displaystyle f_{i}}$

${\displaystyle x_{d}=g_{i}(x_{1},\ x_{2},\ x_{3},\ \dots ,\ x_{d-1},\ x_{d+1},\ \dots ,\ x_{N},\ t),\,}$

y reemplace el en cada ecuación del sistema usando la función anterior. Esto siempre se puede hacer para sistemas físicos generales, siempre que la derivada de sea continua, entonces, según el teorema de la función implícita , la solución está garantizada en algún conjunto abierto. Por tanto, es posible eliminar todas las apariciones de la variable dependiente . ${\displaystyle x_{d}}$ ${\displaystyle f_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle x_{d}}$

Supongamos que un sistema físico tiene grados de libertad. Ahora, se imponen restricciones holonómicas al sistema. Luego, el número de grados de libertad se reduce a . Podemos usar coordenadas generalizadas independientes ( ) para describir completamente el movimiento del sistema. La ecuación de transformación se puede expresar de la siguiente manera: ${\displaystyle N}$ ${\displaystyle h}$ ${\displaystyle m=N-h}$ ${\displaystyle m}$ ${\displaystyle q_{j}}$

${\displaystyle x_{i}=x_{i}(q_{1},\ q_{2},\ \ldots ,\ q_{m},\ t)\ ,\qquad \qquad \qquad i=1,\ 2,\ \ldots N.\,}$

Clasificación de sistemas físicos.

Para estudiar la física clásica de forma rigurosa y metódica, necesitamos clasificar los sistemas. Con base en la discusión anterior, podemos clasificar los sistemas físicos en sistemas holonómicos y sistemas no holonómicos . Una de las condiciones para la aplicabilidad de muchos teoremas y ecuaciones es que el sistema debe ser un sistema holonómico. Por ejemplo, si un sistema físico es un sistema holonómico y un sistema monogénico , entonces el principio de Hamilton es la condición necesaria y suficiente para la corrección de la ecuación de Lagrange . ^[3]

Ver también

• sistema no holonómico
• Goryachev-Chaplygin arriba
• restricción pfaffiana
• Ecuación de Udwadia-Kalaba

Referencias

1. Goldstein, Herbert (2002). "1.3 Restricciones". Mecánica clásica (Tercera ed.). Pearson India: Addison-Wesley. págs. 12-13. ISBN 9788131758915. OCLC  960166650.
2. Goldstein, Herbert (2002). Mecanica clasica . Estados Unidos de América: Addison-Wesley. pag. 46.ISBN​ 978-0-201-65702-9.
3. Goldstein, Herbert (1980). Mecánica clásica (3ª ed.). Estados Unidos de América: Addison Wesley. pag. 45.ISBN​ 0-201-65702-3.