Espacio métrico hiperbólico

Concepto en matemáticas

En matemáticas, un espacio métrico hiperbólico es un espacio métrico que satisface ciertas relaciones métricas (que dependen cuantitativamente de un número real no negativo δ) entre puntos. La definición, introducida por Mikhael Gromov , generaliza las propiedades métricas de la geometría hiperbólica clásica y de los árboles . La hiperbolicidad es una propiedad a gran escala y resulta muy útil para el estudio de ciertos grupos infinitos denominados grupos hiperbólicos de Gromov .

Definiciones

En este párrafo damos varias definiciones de un espacio -hiperbólico. Se dice que un espacio métrico es hiperbólico (de Gromov) si es -hiperbólico para algún . ${\displaystyle \delta }$ ${\displaystyle \delta }$ ${\displaystyle \delta >0}$

Definición utilizando el producto Gromov

Sea un espacio métrico . El producto de Gromov de dos puntos respecto de un tercero se define por la fórmula: ${\displaystyle (X,d)}$ ${\displaystyle y,z\in X}$ ${\displaystyle x\in X}$

${\displaystyle (y,z)_{x}={\frac {1}{2}}\left(d(x,y)+d(x,z)-d(y,z)\right).}$

La definición de Gromov de un espacio métrico hiperbólico es entonces la siguiente: es -hiperbólico si y sólo si todos satisfacen la condición de cuatro puntos. ${\displaystyle X}$ ${\displaystyle \delta }$ ${\displaystyle x,y,z,w\in X}$

${\displaystyle (x,z)_{w}\geq \min \left((x,y)_{w},(y,z)_{w}\right)-\delta }$

Nótese que si esta condición se cumple para todos y un punto base fijo , entonces se cumple para todos con una constante . ^[1] Por lo tanto, la condición de hiperbolicidad solo necesita verificarse para un punto base fijo; por esta razón, el subíndice para el punto base a menudo se omite del producto de Gromov. ${\displaystyle x,y,z\in X}$ ${\displaystyle w_{0}}$ ${\displaystyle }$ ${\displaystyle 2\delta }$

Definiciones usando triángulos

Hasta cambiar por un múltiplo constante, existe una definición geométrica equivalente que involucra triángulos cuando el espacio métrico es geodésico , es decir, dos puntos cualesquiera son puntos finales de un segmento geodésico (una imagen isométrica de un subintervalo compacto de los reales). ^{[2] [3] [4]} Nótese que la definición a través de los productos de Gromov no requiere que el espacio sea geodésico. ${\displaystyle \delta }$ ${\displaystyle X}$ ${\displaystyle x,y\in X}$ ${\displaystyle [x,y]}$ ${\displaystyle [a,b]}$

Sea . Un triángulo geodésico con vértices es la unión de tres segmentos geodésicos (donde denota un segmento con puntos finales y ). ${\displaystyle x,y,z\in X}$ ${\displaystyle x,y,z}$ ${\displaystyle [x,y],[y,z],[z,x]}$ ${\displaystyle [p,q]}$ ${\displaystyle p}$ ${\displaystyle q}$

Si para cualquier punto hay un punto en una distancia menor que de , y de manera similar para los puntos en los otros bordes, entonces se dice que el triángulo es -delgado . ${\displaystyle m\in [x,y]}$ ${\displaystyle [y,z]\cup [z,x]}$ ${\displaystyle \delta }$ ${\displaystyle m}$ ${\displaystyle \delta \geq 0}$ ${\displaystyle \delta }$

La definición de un espacio hiperbólico es entonces la de un espacio métrico geodésico cuyos triángulos geodésicos son todos delgados. Esta definición se atribuye generalmente a Eliyahu Rips . ${\displaystyle \delta }$ ${\displaystyle \delta }$

Otra definición puede darse utilizando la noción de centro -aproximado de un triángulo geodésico: se trata de un punto que se encuentra a una distancia máxima de cualquier borde del triángulo (una versión "aproximada" del incentro ). Un espacio es -hiperbólico si cada triángulo geodésico tiene un -centro. ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle \delta }$ ${\displaystyle \delta }$

Estas dos definiciones de un espacio -hiperbólico que utilizan triángulos geodésicos no son exactamente equivalentes, pero existen tales que un espacio -hiperbólico en el primer sentido es -hiperbólico en el segundo, y viceversa. ^[5] Por lo tanto, la noción de espacio hiperbólico es independiente de la definición elegida. ${\displaystyle \delta }$ ${\displaystyle k>1}$ ${\displaystyle \delta }$ ${\displaystyle k\cdot \delta }$

Ejemplos

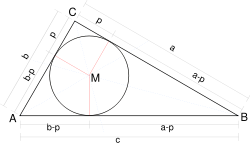
El plano hiperbólico es hiperbólico: de hecho, el incírculo de un triángulo geodésico es el círculo de mayor diámetro contenido en el triángulo y todo triángulo geodésico se encuentra en el interior de un triángulo ideal, todos los cuales son isométricos con incírculos de diámetro 2 log 3. ^[6] Nótese que en este caso el producto de Gromov también tiene una interpretación simple en términos del incírculo de un triángulo geodésico. De hecho, la cantidad ( A , B ) _C es simplemente la distancia hiperbólica p desde C a cualquiera de los puntos de contacto del incírculo con los lados adyacentes: para del diagrama c = ( a – p ) + ( b – p ) , de modo que p = ( a + b – c )/2 = ( A , B ) _C . ^[7]

El plano euclidiano no es hiperbólico, por ejemplo por la existencia de homotecias .

Dos ejemplos "degenerados" de espacios hiperbólicos son los espacios con diámetro acotado (por ejemplo, espacios finitos o compactos) y la línea real.

Los árboles métricos y, en términos más generales, los árboles reales son los ejemplos más simples e interesantes de espacios hiperbólicos, ya que son 0-hiperbólicos (es decir, todos los triángulos son trípodes).

El 1-esqueleto de la triangulación por triángulos equiláteros euclidianos no es hiperbólico (de hecho, es cuasi isométrico al plano euclidiano). Una triangulación del plano tiene un 1-esqueleto hiperbólico si cada vértice tiene grado 7 o más. ${\displaystyle \mathbb {R} ^{2}}$

La cuadrícula bidimensional no es hiperbólica (es casi isométrica respecto del plano euclídeo). Es el grafo de Cayley del grupo fundamental del toro ; el grafo de Cayley de los grupos fundamentales de una superficie de género superior es hiperbólico (es de hecho casi isométrico respecto del plano hiperbólico).

Hiperbolicidad y curvatura

El plano hiperbólico (y más generalmente cualquier variedad de Hadamard de curvatura seccional ) es -hiperbólico. Si escalamos la métrica de Riemann por un factor , las distancias se multiplican por y, por lo tanto, obtenemos un espacio que es -hiperbólico. Como la curvatura se multiplica por, vemos que en este ejemplo, cuanto más (negativamente) curvado es el espacio, menor es la constante de hiperbolicidad. ${\displaystyle \leq -1}$ ${\displaystyle 2}$ ${\displaystyle \lambda >0}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda \cdot \delta }$ ${\displaystyle \lambda ^{-1}}$

Ejemplos similares son los espacios CAT de curvatura negativa. Con respecto a la curvatura y la hiperbolicidad, cabe señalar, sin embargo, que mientras que la curvatura es una propiedad que es esencialmente local, la hiperbolicidad es una propiedad a gran escala que no ve fenómenos métricos locales (es decir, que ocurren en una región limitada). Por ejemplo, la unión de un espacio hiperbólico con un espacio compacto con cualquier métrica que extienda las originales sigue siendo hiperbólica.

Propiedades importantes

Invariancia bajo cuasi-isometría

Una forma de precisar el significado de "gran escala" es exigir invariancia en condiciones de cuasi-isometría . Esto es cierto en el caso de la hiperbolicidad.

Si un espacio métrico geodésico es cuasi isométrico a un espacio -hiperbólico , entonces existe tal que es -hiperbólico. ${\displaystyle Y}$ ${\displaystyle \delta }$ ${\displaystyle X}$ ${\displaystyle \delta '}$ ${\displaystyle Y}$ ${\displaystyle \delta '}$

La constante depende de y de las constantes multiplicativas y aditivas para la cuasi-isometría. ^[8] ${\displaystyle \delta '}$ ${\displaystyle \delta }$

Árboles aproximados en espacios hiperbólicos

La definición de un espacio hiperbólico en términos del producto de Gromov puede interpretarse como que las relaciones métricas entre cuatro puntos cualesquiera son las mismas que las que existirían en un árbol, hasta la constante aditiva . De manera más general, la siguiente propiedad muestra que cualquier subconjunto finito de un espacio hiperbólico se parece a un árbol finito. ${\displaystyle \delta }$

Para cualquier hay una constante tal que se cumple lo siguiente: si son puntos en un espacio -hiperbólico hay un árbol finito y una incrustación tal que para todos y ${\displaystyle n,\delta }$ ${\displaystyle C}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \delta }$ ${\displaystyle X}$ ${\displaystyle T}$ ${\displaystyle f:T\to X}$ ${\displaystyle x_{i}\in f(T)}$ ${\displaystyle i=1,\ldots ,n}$

${\displaystyle \forall i,j:d(f^{-1}(x_{i}),f^{-1}(x_{j}))\leq d(x_{i},x_{j})\leq d(f^{-1}(x_{i}),f^{-1}(x_{j}))+C}$

La constante puede tomarse como con y esto es óptimo. ^[9] ${\displaystyle C}$ ${\displaystyle \delta \cdot h(n)}$ ${\displaystyle h(n)=O(\log n)}$

Crecimiento exponencial de la distancia y desigualdades isoperimétricas

En un espacio hiperbólico tenemos la siguiente propiedad: ^[10] ${\displaystyle X}$

Hay tales que para todos con , cada camino que une y permanece a una distancia de al menos de tiene una longitud de al menos . ${\displaystyle \mu ,K>0}$ ${\displaystyle p,x,y\in X}$ ${\displaystyle d(p,x)=d(p,y)=:r}$ ${\displaystyle \alpha }$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle r}$ ${\displaystyle p}$ ${\displaystyle e^{\mu \cdot d(x,y)}-K}$

De manera informal, esto significa que la circunferencia de un "círculo" de radio crece exponencialmente con . Esto recuerda al problema isoperimétrico en el plano euclidiano . A continuación se presenta una declaración más específica al respecto. ^[11] ${\displaystyle r}$ ${\displaystyle r}$

Supongamos que es un complejo de células de dimensión 2 tal que su 1-esqueleto es hiperbólico, y existe tal que el límite de cualquier 2-célula contiene como máximo 1-células. Entonces existe una constante tal que para cualquier subcomplejo finito tenemos ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle \lambda >0}$ ${\displaystyle Y\subset X}$

${\displaystyle \operatorname {area} (Y)\leq \lambda \cdot \operatorname {length(\partial Y)} }$

Aquí el área de un complejo 2 es el número de celdas 2 y la longitud de un complejo 1 es el número de celdas 1. La afirmación anterior es una desigualdad isoperimétrica lineal ; resulta que tener una desigualdad isoperimétrica de este tipo caracteriza a los espacios hiperbólicos de Gromov. ^[12] Las desigualdades isoperimétricas lineales se inspiraron en las condiciones de cancelación pequeña de la teoría de grupos combinatorios .

Subespacios cuasiconvexos

Se dice que un subespacio de un espacio métrico geodésico es cuasiconvexo si existe una constante tal que cualquier geodésica entre dos puntos de permanece dentro de la distancia de . ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle C}$ ${\displaystyle Y}$

Un subespacio cuasi-convexo de un espacio hiperbólico es hiperbólico.

Conos asintóticos

Todos los conos asintóticos de un espacio hiperbólico son árboles reales . Esta propiedad caracteriza a los espacios hiperbólicos. ^[13]

El límite de un espacio hiperbólico

Generalizando la construcción de los extremos de un árbol simplicial existe una noción natural de límite en el infinito para espacios hiperbólicos, que ha demostrado ser muy útil para analizar acciones de grupo.

En este párrafo hay un espacio métrico geodésico que es hiperbólico. ${\displaystyle X}$

Definición utilizando el producto Gromov

Se dice que una sucesión converge al infinito si para algún punto (o cualquier punto) tenemos que ambos son iguales y tienden al infinito. Dos sucesiones que convergen al infinito se consideran equivalentes cuando (para algún punto o cualquier punto ). El límite de es el conjunto de clases de equivalencia de sucesiones que convergen al infinito, ^[14] que se denota como . ${\displaystyle (x_{n})\in X^{\mathbb {N} }}$ ${\displaystyle p}$ ${\displaystyle (x_{n},x_{m})_{p}\rightarrow \infty }$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle (x_{n}),(y_{n})}$ ${\displaystyle \lim _{n\to +\infty }(x_{n},y_{n})_{p}=+\infty }$ ${\displaystyle p}$ ${\displaystyle X}$ ${\displaystyle \partial X}$

Si hay dos puntos en el límite, entonces su producto de Gromov se define como: ${\displaystyle \xi ,\eta }$

${\displaystyle (\xi ,\eta )_{p}=\sup _{(x_{n})=\xi ,(y_{n})=\eta }\left(\liminf _{n,m\to +\infty }(x_{n},y_{m})_{p}\right)}$

que es finito si y solo si . Se puede entonces definir una topología en utilizando las funciones . ^[15] Esta topología en es metrisable y existe una familia distinguida de métricas definidas utilizando el producto de Gromov. ^[16] ${\displaystyle \xi \neq \eta }$ ${\displaystyle \partial X}$ ${\displaystyle (\cdot ,\xi )}$ ${\displaystyle \partial X}$

Definición de espacios propios mediante rayos

Sean dos incrustaciones cuasi-isométricas de en ("rayos cuasi-geodésicos"). Se consideran equivalentes si y solo si la función está acotada en . Si el espacio es propio, entonces el conjunto de todas esas incrustaciones módulo equivalencia con su topología natural es homeomorfo a como se definió anteriormente. ^[17] ${\displaystyle \alpha ,\beta }$ ${\displaystyle [0,+\infty [}$ ${\displaystyle X}$ ${\displaystyle t\mapsto d(\alpha (t),\beta (t))}$ ${\displaystyle [0,+\infty [}$ ${\displaystyle X}$ ${\displaystyle \partial X}$

Una realización similar es fijar un punto base y considerar solo los rayos cuasi geodésicos que se originan desde este punto. En caso de que sea geodésico y propio, también se puede restringir a los rayos geodésicos genuinos. ${\displaystyle X}$

Ejemplos

Cuando es un árbol regular simplicial el límite es solo el espacio de extremos, que es un conjunto de Cantor. Fijando un punto se obtiene una distancia natural en : dos puntos representados por rayos que se originan en están a una distancia . ${\displaystyle X=T}$ ${\displaystyle x\in T}$ ${\displaystyle \partial T}$ ${\displaystyle \alpha ,\beta }$ ${\displaystyle x}$ ${\displaystyle \exp(-\operatorname {Length} (\alpha \cap \beta ))}$

Cuando el disco unitario, es decir, el modelo de disco de Poincaré para el plano hiperbólico, es la métrica hiperbólica en el disco ${\displaystyle X}$

${\displaystyle ds^{2}={4|dz|^{2} \over (1-|z|^{2})^{2}}}$

y el límite de Gromov se puede identificar con el círculo unitario.

El límite del espacio hiperbólico -dimensional es homeomorfo a la esfera -dimensional y las métricas son similares a la anterior. ${\displaystyle n}$ ${\displaystyle n-1}$

Funciones de Busemann

Si es apropiado entonces su límite es homeomorfo al espacio de funciones de Busemann en traslaciones módulo. ^[18] ${\displaystyle X}$ ${\displaystyle X}$

La acción de las isometrías sobre el límite y su clasificación

Una cuasi-isometría entre dos espacios hiperbólicos induce un homeomorfismo entre los límites. ${\displaystyle X,Y}$

En particular, el grupo de isometrías de actúa por homeomorfismos en . Esta acción puede utilizarse ^[19] para clasificar las isometrías según su comportamiento dinámico en la frontera, generalizando esto para árboles y espacios hiperbólicos clásicos. Sea una isometría de , entonces se da uno de los siguientes casos: ${\displaystyle X}$ ${\displaystyle \partial X}$ ${\displaystyle g}$ ${\displaystyle X}$

• Primer caso: tiene una órbita acotada en (en caso de que sea propiamente dicha esto implica que tiene un punto fijo en ). Entonces se llama isometría elíptica . ${\displaystyle g}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle g}$ ${\displaystyle X}$
• Segundo caso: tiene exactamente dos puntos fijos en y cada órbita positiva se acumula solo en . Entonces se llama isometría hiperbólica . ${\displaystyle g}$ ${\displaystyle \xi _{+},\xi _{-}}$ ${\displaystyle \partial X}$ ${\displaystyle \{g^{n}\xi :n\geq 0\},\xi \not =\xi _{-}}$ ${\displaystyle \xi _{+}}$ ${\displaystyle g}$
• Tercer caso: tiene exactamente un punto fijo en el límite y todas las órbitas se acumulan en ese punto. Entonces se llama isometría parabólica . ${\displaystyle g}$

Más ejemplos

Los subconjuntos de la teoría de grupos hiperbólicos se pueden utilizar para dar más ejemplos de espacios hiperbólicos, por ejemplo, el gráfico de Cayley de un pequeño grupo de cancelación . También se sabe que los gráficos de Cayley de ciertos modelos de grupos aleatorios (que en realidad son gráficos regulares infinitos generados aleatoriamente) tienden a ser hiperbólicos muy a menudo.

Puede resultar difícil e interesante demostrar que ciertos espacios son hiperbólicos. Por ejemplo, los siguientes resultados de hiperbolicidad han llevado al descubrimiento de nuevos fenómenos para los grupos que actúan en ellos.

• La hiperbolicidad del complejo de curvas ^[20] ha llevado a nuevos resultados sobre el grupo de clases de mapeo. ^[21]
• De manera similar, la hiperbolicidad de ciertos grafos ^[22] asociados al grupo de automorfismos externos Out(Fn) ha llevado a nuevos resultados sobre este grupo.

Véase también

• Grupo de curvatura negativa
• Triángulo ideal

Notas

1. Coornaert, Delzant y Papadopoulos 1990, págs. 2-3
2. de la Harpe & Ghys 1990, Capítulo 2, Proposición 21.
3. Bridson y Haefliger 1999, Capítulo III.H, Proposición 1.22.
4. Coornaert, Delzant y Papadopoulos 1990, págs. 6-8.
5. Bridson y Haefliger 1999, Capítulo III.H, Proposición 1.17.
6. Coornaert, Delzant y Papadopoulos 1990, págs. 11-12
7. Coornaert, Delzant y Papadopoulos 1990, págs. 1 y 2
8. de la Harpe & Ghys 1990, Capítulo 5, Proposición 15.
9. Bowditch 2006, Capítulo 6.4.
10. Bridson y Haefliger 1999, Capítulo III.H, Proposición 1.25.
11. Una declaración más general se da en Bridson y Haefliger (1999, Capítulo III.H, Proposición 2.7)
12. Bridson y Haefliger 1999, Capítulo III.H, Teorema 2.9.
13. Dyubina (Erschler), Anna; Polterovich, Iosif (2001). "Construcciones explícitas de árboles R universales y geometría asintótica de espacios hiperbólicos". Bull. London Math. Soc . Vol. 33. págs. 727–734. MR  1853785.
14. de la Harpe & Ghys 1990, capítulo 7, página 120.
15. de la Harpe & Ghys 1990, capítulo 7, sección 2.
16. de la Harpe & Ghys 1990, capítulo 7, sección 3.
17. de la Harpe & Ghys 1990, Capítulo 7, Proposición 4.
18. Bridson y Haefliger 1999, pág. 428.
19. de la Harpe & Ghys 1990, capítulo 8.
20. Masur, Howard A.; Minsky, Yair N. (1999). "Geometría del complejo de curvas. I. Hiperbolicidad". Invent. Math. Vol. 138. págs. 103–149. doi :10.1007/s002220050343. MR  1714338.
21. Dahmani, François; Guirardel, Vincent; Osin, Denis (2017). "Subgrupos incrustados hiperbólicamente y familias rotatorias en grupos que actúan en espacios hiperbólicos". Memorias de la American Mathematical Society . 245 (1156). arXiv : 1111.7048 . doi :10.1090/memo/1156.
22. Bestvina, Mladen; Feighn, Mark (2014). "Hiperbolicidad del complejo de factores libres". Avances en Matemáticas . 256 : 104–155. arXiv : 1107.3308 . doi : 10.1016/j.aim.2014.02.001 . MR  3177291.

Referencias

• Bowditch, Brian (2006), Un curso sobre teoría geométrica de grupos (PDF) , Mat. soc. Japón
• Bridson, Martin R.; Haefliger, André (1999), Espacios métricos de curvatura no positiva , Springer
• Coornaert, M.; Delzant, T.; Papadopoulos, A. (1990), Géométrie et théorie des groupes. Les groupes hyperboliques de Gromov , Lecture Notes in Mathematics (en francés), vol. 1441, Springer-Verlag, ISBN 3-540-52977-2
• de la Harpe, Pierre; Ghys, Etienne (1990), Sur les groupes hyperboliques d'après Mikhael Gromov (en francés), Birkhäuser
• Gromov, Mikhael (1987), "Grupos hiperbólicos", en Gersten, SM (ed.), Ensayos sobre teoría de grupos , Springer, págs. 75-264
• Roe, John (2003), Lecciones sobre geometría gruesa , Serie de conferencias universitarias, vol. 31, American Mathematical Society , ISBN 978-0-8218-3332-2
• Väisälä, Jussi (2005), "Espacios hiperbólicos de Gromov", Expositiones Mathematicae , 23 (3): 187–231, doi : 10.1016/j.exmath.2005.01.010 , SEÑOR  2164775.