Grupo hiperoctaédrico

Grupo de simetrías de un hipercubo n-dimensional.

En matemáticas , un grupo hiperoctaédrico es un tipo importante de grupo que puede realizarse como el grupo de simetrías de un hipercubo o de un politopo cruzado . Fue nombrado por Alfred Young en 1930. Los grupos de este tipo se identifican mediante un parámetro n , la dimensión del hipercubo.

Como grupo de Coxeter es de tipo B _n = C _n , y como grupo de Weyl está asociado a los grupos simplécticos y a los grupos ortogonales en dimensiones impares. Como producto de corona es donde S _n es el grupo simétrico de grado n . Como grupo de permutaciones , el grupo es el grupo simétrico con signo de permutaciones  π del conjunto o del conjunto tal que para todo  i . Como grupo de matrices , puede describirse como el grupo de matrices ortogonales de n × n cuyas entradas son todas números enteros . De manera equivalente, este es el conjunto de matrices n × n con entradas solo 0, 1 o –1, que son invertibles y que tienen exactamente una entrada distinta de cero en cada fila o columna. La teoría de la representación del grupo hiperoctaédrico fue descrita por (Young 1930) según (Kerber 1971, p. 2). ${\displaystyle S_{2}\wr S_{n}}$ ${\displaystyle \{-n,-n+1,\cdots ,-1,1,2,\cdots ,n\}}$ ${\displaystyle \{-n,-n+1,\cdots ,n\}}$ ${\displaystyle \pi (i)=-\pi (-i)}$

En tres dimensiones, el grupo hiperoctaédrico se conoce como O × S ₂ donde O ≅ S ₄ es el grupo octaédrico , y S ₂ es un grupo simétrico (aquí un grupo cíclico ) de orden 2. Figuras geométricas en tres dimensiones con este grupo de simetría Se dice que tienen simetría octaédrica , llamada así por el octaedro regular , o 3- ortoplex . En 4 dimensiones se llama simetría hexadecacórica , en honor a la simetría regular de 16 celdas o 4- ortoplex . En dos dimensiones, la estructura del grupo hiperoctaédrico es el grupo diédrico abstracto de orden ocho , que describe la simetría de un cuadrado o 2-ortoplex.

Por dimensión

Las 8 permutaciones del cuadrado, formando D ₄

8 de las 48 permutaciones de un cubo, formando O _h

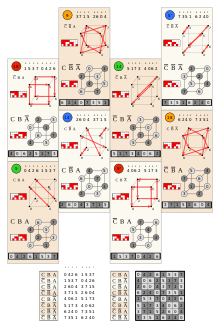
Los grupos hiperoctaédricos se pueden nombrar como B n , una notación entre corchetes o como un gráfico de grupo de Coxeter:

Subgrupos

Hay un subgrupo de índice notable dos, correspondiente al grupo de Coxeter D _n y las simetrías del demihipercubo . Visto como un producto de corona, hay dos mapas naturales desde el grupo hiperoctaédrico al grupo cíclico de orden 2: un mapa proveniente de "multiplicar los signos de todos los elementos" (en las n copias de ), y un mapa proveniente de paridad de la permutación. Multiplicarlos produce un tercer mapa . El núcleo del primer mapa es el grupo de Coxeter. En términos de permutaciones con signo , consideradas matrices, este tercer mapa es simplemente el determinante, mientras que los dos primeros corresponden a "multiplicar las entradas distintas de cero" y "paridad del subyacente ( unsigned) permutation", que generalmente no son significativos para matrices, pero en el caso se deben a la coincidencia con un producto de corona. ${\displaystyle \{\pm 1\}}$ ${\displaystyle C_{n}\to \{\pm 1\}}$ ${\displaystyle D_{n}.}$

Los núcleos de estos tres mapas son los tres subgrupos del índice dos del grupo hiperoctaédrico, como se analiza en H1: Abelianización a continuación, y su intersección es el subgrupo derivado , del índice 4 (cociente del grupo 4 de Klein), que corresponde a la rotación. Simetrías del semihipercubo.

En la otra dirección, el centro es el subgrupo de matrices escalares, {±1}; geométricamente, cociente por esto corresponde a pasar al grupo ortogonal proyectivo .

En la dimensión 2, estos grupos describen completamente el grupo hiperoctaédrico, que es el grupo diédrico Dih ₄ de orden 8 , y es una extensión 2.V (del grupo 4 por un grupo cíclico de orden 2). En general, pasar al subcociente (subgrupo derivado, centro mod) es el grupo de simetría del demihipercubo proyectivo.

Simetría tetraédrica en tres dimensiones, orden 24

El subgrupo hiperoctaédrico , D _n por dimensión:

Simetría piritoédrica en tres dimensiones, orden 24

Simetría octaédrica en tres dimensiones, orden 24

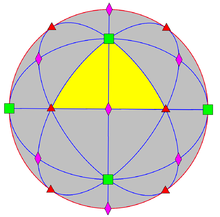
La simetría hiperoctaédrica quiral , es el subgrupo directo, índice 2 de la simetría hiperoctaédrica.

Otro subgrupo notable del índice 2 puede denominarse simetría hiperpiritoédrica , por dimensión: ^[5] Estos grupos tienen n espejos ortogonales en n dimensiones.

Homología

La homología de grupo del grupo hiperoctaédrico es similar a la del grupo simétrico y exhibe estabilización, en el sentido de la teoría de la homotopía estable .

H 1 : abelianización

El primer grupo de homología, que concuerda con la abelianización , se estabiliza en el grupo de cuatro de Klein y viene dado por:

${\displaystyle H_{1}(C_{n},\mathbf {Z} )={\begin{cases}0&n=0\\\mathbf {Z} /2&n=1\\\mathbf {Z} /2\times \mathbf {Z} /2&n\geq 2\end{cases}}.}$

Esto se ve fácilmente de manera directa: los elementos son de orden 2 (que no están vacíos para ) y todos son conjugados, al igual que las transposiciones en (que no están vacías para ), y estas son dos clases separadas. Estos elementos generan el grupo, por lo que las únicas abelianizaciones no triviales son para 2 grupos, y cualquiera de estas clases se puede enviar de forma independiente, ya que son dos clases separadas. Los mapas se dan explícitamente como "el producto de los signos de todos los elementos" (en las n copias de ) y el signo de la permutación. Al multiplicarlos se obtiene un tercer mapa no trivial (el determinante de la matriz, que envía ambas clases a ), y junto con el mapa trivial, forman el grupo 4. ${\displaystyle -1}$ ${\displaystyle n\geq 1}$ ${\displaystyle S_{n}}$ ${\displaystyle n\geq 2}$ ${\displaystyle -1\in \{\pm 1\},}$ ${\displaystyle \{\pm 1\}}$ ${\displaystyle -1}$

H 2 : Multiplicadores de Schur

Los segundos grupos de homología, conocidos clásicamente como multiplicadores de Schur , se calcularon en (Ihara y Yokonuma 1965).

Ellos son:

${\displaystyle H_{2}(C_{n},\mathbf {Z} )={\begin{cases}0&n=0,1\\\mathbf {Z} /2&n=2\\(\mathbf {Z} /2)^{2}&n=3\\(\mathbf {Z} /2)^{3}&n\geq 4\end{cases}}.}$

Notas

1. Conway y Smith 2003
2. du Val 1964, n.° 47
3. du Val 1964, n.° 42
4. du Val 1964, n.° 27
5. Coxeter 1999, pag. 121, Ensayo 5 Poliedros sesgados regulares
6. du Val 1964, n.° 41

Referencias

• Miller, GA (1918). "Grupos formados por matrices especiales". Toro. Soy. Matemáticas. Soc . 24 (4): 203–6. doi : 10.1090/S0002-9904-1918-03043-7 .
• du Val, P. (1964). Homografías, Cuaterniones y Rotaciones. Monografías matemáticas de Oxford. Prensa de Clarendon. OCLC  904102141.
• Ihara, Shin-ichiro; Yokonuma, Takeo (1965), "Sobre los segundos grupos de cohomología (multiplicadores de Schur) de grupos de reflexión finitos", Revista de la Facultad de Ciencias. Universidad de Tokio. Sección IA. Matemáticas , 11 : 155–171, ISSN  0040-8980, SEÑOR  0190232
• Kerber, Adalbert (1971), Representaciones de grupos de permutación. I , Apuntes de conferencias de matemáticas, vol. 240, Springer-Verlag , doi :10.1007/BFb0067943, ISBN 978-3-540-05693-5, SEÑOR  0325752
• Kerber, Adalbert (1975), Representaciones de grupos de permutación. II , Apuntes de conferencias de matemáticas, vol. 495, Springer-Verlag , doi :10.1007/BFb0085740, ISBN 978-3-540-07535-6, SEÑOR  0409624
• Young, Alfred (1930), "On Quantitative Sustitutional Analysis 5", Actas de la London Mathematical Society , Serie 2, 31 : 273–288, doi :10.1112/plms/s2-31.1.273, ISSN  0024-6115, JFM  56.0135 .02
• Coxeter, HSM; Moser, WOJ (2013) [1980]. Generadores y relaciones para grupos discretos (4ª ed.). Saltador. pag. 92 §7.4 Grupos fraccionarios lineales, p. 122 §9.3 Grupos finitos. ISBN 978-3-662-21943-0.
• Baake, M. (1984). "Estructura y representaciones del grupo hiperoctaédrico". J. Matemáticas. Física . 25 (11): 3171. Código bibliográfico : 1984JMP....25.3171B. doi : 10.1063/1.526087.
• Stembridge, John R. (1992). "Las representaciones proyectivas del grupo hiperoctaédrico". J. Álgebra . 145 (2): 396–453. doi :10.1016/0021-8693(92)90110-8. hdl : 2027.42/30235 .
• Coxeter, HSM (1999). La belleza de la geometría: doce ensayos . Dover. ISBN 0-486-40919-8. LCCN  99035678.
• Conway, John H .; Smith, Derek A. (2003). Sobre cuaterniones y octoniones. Prensa CRC. ISBN 978-1-000-68777-4.