pose graduada

Un conjunto de potencias , parcialmente ordenado por inclusión , con rango definido como número de elementos, forma un poset graduado.

En matemáticas , en la rama de la combinatoria , un poset graduado es un conjunto parcialmente ordenado (poset) P equipado con una función de rango ρ desde P hasta el conjunto N de todos los números naturales . ρ debe satisfacer las dos propiedades siguientes:

• La función de rango es compatible con el orden, lo que significa que para todos los x e y en el orden, si x  <  y entonces ρ ( x ) <  ρ ( y ), y
• El rango es consistente con la relación de cobertura del orden, lo que significa que para todo x e y , si y cubre x entonces ρ ( y ) =  ρ ( x ) + 1.

El valor de la función de rango para un elemento del poset se llama rango . A veces, un poset clasificado se denomina poset clasificado, pero esa frase tiene otros significados; ver poset clasificado . Un rango o nivel de rango de un poset graduado es el subconjunto de todos los elementos del poset que tienen un valor de rango determinado. ^{[1] [2]}

Los posets graduados juegan un papel importante en combinatoria y pueden visualizarse mediante un diagrama de Hasse .

Ejemplos

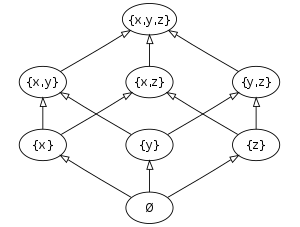
Algunos ejemplos de posets graduados (con la función de rango entre paréntesis) son:

• Números naturales N con su orden habitual (rango: el número mismo), o algún intervalo [0,  N ] de este poset
• N ⁿ con el orden del producto (suma de los componentes), o un subconjunto del mismo que sea producto de intervalos
• Enteros positivos ordenados por divisibilidad (número de factores primos , contados con multiplicidad), o un subconjunto del mismo formado por los divisores de un N fijo
• La red booleana de subconjuntos finitos de un conjunto ordenado por inclusión (número de elementos del subconjunto)
• Cualquier red distributiva de conjuntos inferiores finitos de otro poset (número de elementos)
  • En particular, cualquier red distributiva finita.
• Poset de todos los posets sin etiquetar en (número de elementos) ^[3] ${\displaystyle \{1,...,n\}}$
• Red de Young (número de cuadros en el diagrama de Young)
• Cualquier red geométrica , como la red de subespacios de un espacio vectorial ( dimensión del subespacio)
• Red de particiones de un conjunto en un número finito de partes, ordenadas por refinamiento inverso (número de partes)
• Celosía de particiones de un conjunto finito X , ordenadas por refinamiento (número de elementos de X menos número de partes)
• Red de caras de politopos convexos (dimensión de la cara, más uno)
• Politopo abstracto ("distancia" desde la menor cara, menos uno)
• Complejo simplicial abstracto (número de elementos del simplex)
• Un grupo con un conjunto generador , o equivalentemente su gráfico Cayley , ordenado por el orden Bruhat débil o fuerte , y clasificado por longitud de palabra (longitud de la palabra reducida más corta)
  • En particular, un grupo de Coxeter , por ejemplo, permutaciones de un conjunto de n elementos totalmente ordenado , con orden de Bruhat débil o fuerte (número de inversiones adyacentes)

Caracterizaciones alternativas

La red N ₅ no se puede nivelar.

Un poset acotado ^[4] admite una clasificación si y sólo si todas las cadenas máximas en P tienen la misma longitud: ^[5] establecer el rango del elemento mínimo en 0 determina la función de rango completamente. Esto cubre muchos casos finitos de interés; vea la imagen para ver un ejemplo negativo. Sin embargo, los posets ilimitados pueden ser más complicados.

Una función de rango candidata, compatible con el ordenamiento, convierte un poset en poset graduado si y sólo si, siempre que se tenga x  <  z con z de rango n  + 1, se puede encontrar un elemento y de rango n con x  ≤  y  <  z . Esta condición es suficiente porque si se toma z como una cobertura de x , la única opción posible es y  =  x, lo que muestra que los rangos de x y z difieren en 1, y es necesaria porque en un poset graduado se puede tomar por y cualquier elemento de rango máximo con x  ≤  y  <  z , que siempre existe y está cubierto por z .

A menudo, un poset viene con un candidato natural para una función de rango; por ejemplo, si sus elementos son subconjuntos finitos de algún conjunto base B , se puede tomar el número de elementos de esos subconjuntos. Entonces el criterio que acabamos de dar puede ser más práctico que la definición porque evita mencionar las coberturas. Por ejemplo, si B es en sí mismo un poset, y P consta de sus conjuntos inferiores finitos (subconjuntos para los cuales con cada uno de sus elementos, todos los elementos más pequeños también están en el subconjunto), entonces el criterio se satisface automáticamente, ya que para conjuntos inferiores x  ⊆  z siempre hay un elemento máximo de z que está ausente en x y se puede eliminar de z para formar y .

En algunos posets comunes, como la red de caras de un politopo convexo, existe una clasificación natural por dimensión , que si se usa como función de rango daría al elemento mínimo, la cara vacía, rango −1. En tales casos, podría ser conveniente modificar la definición establecida anteriormente adjuntando el valor −1 al conjunto de valores permitidos para la función de rango. Sin embargo, permitir números enteros arbitrarios como rango daría una noción fundamentalmente diferente; por ejemplo, ya no estaría asegurada la existencia de un elemento mínimo.

Un poset graduado (con rangos enteros positivos) no puede tener ningún elemento x para el cual existan cadenas arbitrariamente largas con el mayor elemento x , de lo contrario tendría que tener elementos de rango arbitrariamente pequeño (y eventualmente negativo). Por ejemplo, los números enteros (con el orden habitual) no pueden ser un poset graduado, ni tampoco cualquier intervalo (con más de un elemento) de números racionales o reales . (En particular, los posets graduados están bien fundamentados , lo que significa que satisfacen la condición de cadena descendente (DCC): no contienen cadenas descendentes infinitas . ^[6] ) De ahora en adelante, solo consideraremos posets en los que esto no suceda. Esto implica que siempre que x  <  y podemos pasar de x a y eligiendo repetidamente una cobertura, un número finito de veces. También significa que (para funciones de rango entero positivo) la compatibilidad de ρ con el orden se deriva del requisito sobre las coberturas. Como variante de la definición de poset graduado, Birkhoff ^[7] permite que las funciones de rango tengan valores enteros arbitrarios (en lugar de sólo no negativos). En esta variante, los números enteros se pueden clasificar (mediante la función de identidad) en su configuración, y la compatibilidad de los rangos con el orden no es redundante. Como tercera variante, Brightwell y West ^[8] definen una función de rango como de valor entero, pero no requieren su compatibilidad con el orden; por lo tanto, esta variante puede clasificar incluso, por ejemplo, los números reales mediante cualquier función, ya que el requisito sobre las coberturas no es válido para este ejemplo.

Tenga en cuenta que los posets graduados no necesitan satisfacer la condición de cadena ascendente (ACC): por ejemplo, los números naturales contienen la cadena ascendente infinita . ${\displaystyle 0<1<2<\dots }$

Un poset se califica si y solo si cada componente conectado de su gráfico de comparabilidad está calificado, por lo que caracterizaciones adicionales supondrán que este gráfico de comparabilidad está conectado. En cada componente conectado, la función de rango solo es única hasta un cambio uniforme (por lo que la función de rango siempre se puede elegir de modo que los elementos de rango mínimo en su componente conectado tengan rango 0).

Si P tiene un elemento mínimo Ô, entonces calificar es equivalente a la condición de que para cualquier elemento x todas las cadenas máximas en el intervalo [Ô,  x ] tengan la misma longitud. Esta condición es necesaria ya que cada paso en una cadena máxima es una relación de cobertura, que debería cambiar el rango en 1. La condición también es suficiente, ya que cuando se cumple, se puede usar la longitud mencionada para definir el rango de x (la longitud de una cadena finita es su número de "pasos", por lo que uno menos que su número de elementos), y siempre que x cubra y , unir x a una cadena máxima en [Ô, y ] da una cadena máxima en [Ô, x ] .

Si P también tiene un elemento mayor Î (de modo que es un poset acotado ), entonces la condición anterior se puede simplificar al requisito de que todas las cadenas máximas en P tengan la misma longitud (finita). Esto es suficiente, ya que cualquier par de cadenas máximas en [Ô, x ] puede extenderse mediante una cadena máxima en [ x , Î] para dar un par de cadenas máximas en P.

Nota Stanley define un poset como clasificado de longitud n si todas sus cadenas máximas tienen longitud n (Stanley 1997, p.99). Esta definición se da en un contexto donde el interés se centra principalmente en posets finitos, y aunque posteriormente el libro a menudo elimina la parte "de longitud n ", no parece apropiado usar esto como definición de "calificado" para posets generales, porque ( 1) no dice nada sobre posets cuyas cadenas máximas son infinitas, en particular (2) excluye posets importantes como la red de Young . Tampoco está claro por qué en un poset graduado se debe exigir que todos los elementos mínimos, así como todos los elementos máximos, tengan la misma longitud, incluso si Stanley da ejemplos que dejan claro que sí pretende exigir eso (ibid, pp.216). y 219).

El caso habitual

Muchos autores en combinatoria definen posets graduados de tal manera que todos los elementos mínimos de P deben tener rango 0 y, además, existe un rango máximo r que es el rango de cualquier elemento máximo. Entonces, estar clasificado significa que todas las cadenas máximas tienen una longitud r , como se indica arriba. En este caso se dice que P tiene rango r .

Además, en este caso, a los niveles de rango se asocian los números de rango o números de Whitney . Estos números se definen por = número de elementos de P que tienen rango i . ${\displaystyle W_{0},W_{1},W_{2},...}$ ${\displaystyle W_{i}}$

Los números de Whitney están relacionados con muchos teoremas combinatorios importantes . El ejemplo clásico es el teorema de Sperner , que se puede formular de la siguiente manera:

Para el conjunto potencia de cada conjunto finito, la cardinalidad máxima de una familia de Sperner es igual al número máximo de Whitney . ${\displaystyle {\mathcal {P}}(S)}$ ${\displaystyle S}$

Esto significa:

Todo conjunto de potencias finitas tiene la propiedad de Sperner.

Ver también

• Calificado (matemáticas)
• Prewellordering : un prewellordering con una norma es análogo a un poset graduado, reemplazando un mapa de números enteros con un mapa de ordinales.
• Producto estrella , un método para combinar dos posets graduados

Notas

1. Stanley, Richard (1984), "Cocientes de posets de Peck", Orden , 1 (1): 29–34, doi :10.1007/BF00396271, MR  0745587, S2CID  14857863.
2. Butler, Lynne M. (1994), Redes de subgrupos y funciones simétricas, Memorias de la Sociedad Matemática Estadounidense, vol. 539, Sociedad Estadounidense de Matemáticas, pág. 151, ISBN 9780821826003.
3. Culberson, José C.; Rawlins, Gregory JE (1990), "Nuevos resultados de un algoritmo para contar posets", Orden , 7 (4): 361–374, doi :10.1007/BF00383201, S2CID  120473635
4. Lo que significa que tiene un elemento mínimo y un elemento mayor .
5. Es decir, no tenemos una situación en la que y ambas sean cadenas máximas. ${\displaystyle x<z_{1}<y}$ ${\displaystyle x<w_{1}<w_{2}<y}$
6. No contener cadenas descendentes arbitrariamente largas que comiencen en un elemento fijo, por supuesto, excluye cualquier cadena descendente infinita. Sin embargo, la primera condición es estrictamente más fuerte; el conjunto tiene cadenas arbitrariamente largas que descienden de  , pero no tiene cadenas descendentes infinitas. ${\displaystyle \mathbb {N} \cup \{\infty \}}$ ${\displaystyle \infty }$
7. 'Teoría de la celosía', Am. Matemáticas. Soc., Publicaciones del Coloquio, Vol.25, 1967, p.5
8. Ver referencia [2], p.722.

Referencias

• Stanley, Richard (1997). Combinatoria enumerativa (vol.1, Estudios de Cambridge en Matemáticas Avanzadas 49) . Prensa de la Universidad de Cambridge . ISBN 0-521-66351-2.
• Anderson, Ian (1987). Combinatoria de conjuntos finitos . Oxford, Reino Unido: Clarendon Press . ISBN 0-19-853367-5.
• Engel, Konrad (1997). Teoría de Sperner . Cambridge, Reino Unido (et al.): Cambridge University Press. ISBN 0-521-45206-6.
• Kung, Joseph PS; Rota, Gian-Carlo ; Yan, Catherine H. (2009). Combinatoria: el estilo Rota . Cambridge, Reino Unido (et al.): Cambridge University Press. ISBN 978-0-521-73794-4.