Un gráfico existencial es un tipo de notación diagramática o visual para expresiones lógicas, creado por Charles Sanders Peirce , quien escribió sobre lógica gráfica en 1882, [1] y continuó desarrollando el método hasta su muerte en 1914. Incluyen una notación gráfica separada para declaraciones lógicas y un cálculo lógico, un sistema formal de reglas de inferencia que se pueden utilizar para derivar teoremas.
Peirce consideraba que la notación algebraica (es decir, la notación simbólica) de la lógica, especialmente la de predicados [2] , que todavía era muy nueva en su época y en cuyo desarrollo él mismo desempeñó un papel importante, era filosóficamente insatisfactoria, porque los símbolos tenían su significado por mera convención. Por el contrario, se esforzaba por lograr un estilo de escritura en el que los signos llevaran literalmente su significado dentro de ellos [3] –en la terminología de su teoría de los signos: un sistema de signos icónicos que se asemejan o se asemejan a los objetos y relaciones representados. [4]
Así, el desarrollo de un sistema lógico icónico, gráfico y –como pretendía– intuitivo y fácil de aprender fue un proyecto en el que Peirce trabajó durante toda su vida. Después de al menos un enfoque abortado –los “grafos entitativos”–, el sistema cerrado de los “grafos existenciales” finalmente surgió a partir de 1896. Aunque su creador los consideró un sistema claramente superior y más intuitivo, como modo de escritura y como cálculo, no tuvieron una influencia importante en la historia de la lógica. Esto se ha atribuido al hecho de que, por un lado, Peirce publicó poco sobre este tema y que los textos publicados no estaban escritos de una manera muy comprensible; [5] y, por otro lado, que la notación de fórmulas lineales en manos de expertos es en realidad la herramienta menos compleja. [6] Por lo tanto, los grafos existenciales recibieron poca atención [7] o se los consideró difíciles de manejar. [8] A partir de 1963, los trabajos de Don D. Roberts y J. Jay Zeman, en los que se examinaron y presentaron sistemáticamente los sistemas gráficos de Peirce, permitieron una mejor comprensión; aun así, hoy en día han encontrado un uso práctico en una sola aplicación moderna: los grafos conceptuales introducidos por John F. Sowa en 1976, que se utilizan en informática para representar el conocimiento. Sin embargo, los grafos existenciales están reapareciendo cada vez más como tema de investigación en relación con un creciente interés en la lógica gráfica, [9] que también se expresa en los intentos de reemplazar las reglas de inferencia dadas por Peirce por otras más intuitivas. [10]
El sistema general de grafos existenciales se compone de tres subsistemas que se complementan entre sí: los grafos alfa, beta y gamma. Los grafos alfa son un sistema de lógica puramente proposicional, y los grafos beta, a partir de este, constituyen un cálculo lógico de primer orden. Los grafos gamma, que aún no han sido completamente investigados y no fueron completados por Peirce, se entienden como un desarrollo posterior de los grafos alfa y beta. Cuando se interpretan adecuadamente, los grafos gamma abarcan la lógica de predicados de nivel superior, así como la lógica modal. En 1903, Peirce comenzó un nuevo enfoque, los "grafos existenciales teñidos", con los que quería reemplazar los sistemas anteriores de grafos alfa, beta y gamma y combinar su expresividad y rendimiento en un único sistema nuevo. Al igual que los grafos gamma, los "grafos existenciales teñidos" quedaron inacabados.
Como cálculos, los grafos alfa, beta y gamma son válidos (es decir, todas las expresiones derivadas como grafos son semánticamente válidas). Los grafos alfa y beta también son completos (es decir, todas las expresiones proposicionales o predicativamente-lógicamente válidas semánticamente pueden derivarse como grafos alfa o beta). [11]
Peirce propuso tres sistemas de grafos existenciales:
Alfa se anida en beta y gamma . Beta no se anida en gamma , siendo la lógica modal cuantificada más general que la propuesta por Peirce.
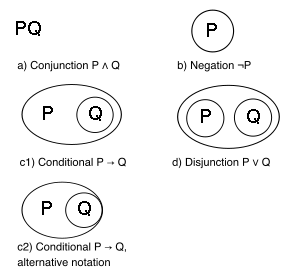
La sintaxis es:
Cualquier parte bien formada de un gráfico es un subgráfico .
La semántica es:
Por lo tanto, los grafos alfa son una notación minimalista para la lógica oracional , basada en la adecuación expresiva de And y Not . Los grafos alfa constituyen una simplificación radical del álgebra booleana de dos elementos y los funtores de verdad .
La profundidad de un objeto es el número de cortes que lo encierran.
Reglas de inferencia :
Reglas de equivalencia :
Una demostración manipula un gráfico mediante una serie de pasos, cada uno de los cuales se justifica mediante una de las reglas anteriores. Si un gráfico se puede reducir por pasos hasta llegar a una página en blanco o a un corte vacío, se trata de lo que ahora se denomina una tautología (o su complemento, una contradicción). Los gráficos que no se pueden simplificar más allá de un cierto punto son análogos de las fórmulas satisfacibles de la lógica de primer orden .


En el caso de los betagrafos, las expresiones atómicas ya no son letras proposicionales (P, Q, R,...) o enunciados ("Llueve", "Peirce murió en la pobreza"), sino predicados en el sentido de la lógica de predicados (ver allí para más detalles), posiblemente abreviados a letras de predicado (F, G, H,...). Un predicado en el sentido de la lógica de predicados es una secuencia de palabras con espacios claramente definidos que se convierte en una oración proposicional si se inserta un nombre propio en cada espacio. Por ejemplo, la secuencia de palabras "_ x es un humano" es un predicado porque da lugar a la oración declarativa "Peirce es un humano" si se introduce el nombre propio "Peirce" en el espacio en blanco. Del mismo modo, la secuencia de palabras "_ 1 es más rico que _ 2 " es un predicado, porque da lugar al enunciado "Sócrates es más rico que Platón" si se insertan los nombres propios "Sócrates" o "Platón" en los espacios.
El recurso lingüístico básico es la línea de identidad, una línea gruesa de cualquier forma. La línea de identidad se acopla al espacio en blanco de un predicado para mostrar que el predicado se aplica al menos a un individuo. Para expresar que el predicado "_ es un ser humano" se aplica al menos a un individuo –es decir, para decir que hay (al menos) un ser humano– se escribe una línea de identidad en el espacio en blanco del predicado "_ es un ser humano":
Los gráficos beta pueden leerse como un sistema en el que todas las fórmulas deben considerarse cerradas, porque todas las variables están cuantificadas implícitamente. Si la parte "más superficial" de una línea de identidad tiene una profundidad uniforme, la variable asociada se cuantifica tácitamente existencialmente ( universalmente ).
Zeman (1964) fue el primero en señalar que los grafos beta son isomorfos a la lógica de primer orden con igualdad (véase también Zeman 1967). Sin embargo, la literatura secundaria, especialmente Roberts (1973) y Shin (2002), no está de acuerdo en cómo esto es así. Los escritos de Peirce no abordan esta cuestión, porque la lógica de primer orden fue articulada claramente por primera vez sólo después de su muerte, en la primera edición de 1928 de los Principios de lógica matemática de David Hilbert y Wilhelm Ackermann .
Añade a la sintaxis de alfa un segundo tipo de curva cerrada simple , escrita utilizando una línea discontinua en lugar de una línea continua. Peirce propuso reglas para este segundo estilo de corte, que pueden leerse como el operador unario primitivo de la lógica modal .
Zeman (1964) fue el primero en notar que los grafos gamma son equivalentes a las conocidas lógicas modales S4 y S5 . Por lo tanto, los grafos gamma pueden leerse como una forma peculiar de lógica modal normal . Este hallazgo de Zeman ha recibido poca atención hasta el día de hoy, pero no obstante se incluye aquí como un punto de interés.
Los grafos existenciales son una curiosa descendencia de Peirce, el lógico /matemático, siendo Peirce el fundador de una importante rama de la semiótica . La lógica gráfica de Peirce es sólo uno de sus muchos logros en lógica y matemáticas. En una serie de artículos que comenzaron en 1867 y culminaron con su artículo clásico en el American Journal of Mathematics de 1885 , Peirce desarrolló gran parte del álgebra de Boole de dos elementos , el cálculo proposicional , la cuantificación y el cálculo de predicados , y algo de teoría de conjuntos rudimentaria . Los teóricos de modelos consideran a Peirce el primero de su tipo. También amplió el álgebra de relaciones de De Morgan . Se quedó corto en la metalógica (que eludió incluso los Principia Mathematica ).
Pero la teoría semiótica en evolución de Peirce lo llevó a dudar del valor de la lógica formulada utilizando la notación lineal convencional y a preferir que la lógica y las matemáticas se notaran en dos (o incluso tres) dimensiones. Su trabajo fue más allá de los diagramas de Euler y la revisión de Venn de 1880 de los mismos. La obra de Frege de 1879 Begriffsschrift también empleó una notación bidimensional para la lógica, pero una muy diferente de la de Peirce.
El primer artículo publicado de Peirce sobre lógica gráfica (reimpreso en el vol. 3 de sus Collected Papers ) proponía un sistema dual (en efecto) de los grafos existenciales alfa , llamados grafos entitativos . Muy pronto abandonó este formalismo en favor de los grafos existenciales. En 1911, Victoria, Lady Welby mostró los grafos existenciales a CK Ogden , quien consideró que podrían combinarse de manera útil con los pensamientos de Welby en una "forma menos abstrusa". [12] Por lo demás, atrajeron poca atención durante su vida y fueron invariablemente denigrados o ignorados después de su muerte, hasta las tesis doctorales de Roberts (1964) y Zeman (1964).
Actualmente, la edición crítica cronológica de las obras de Peirce, los Escritos , se extiende sólo hasta 1892. Gran parte del trabajo de Peirce sobre gráficos lógicos consiste en manuscritos escritos después de esa fecha y aún no publicados. Por lo tanto, es probable que nuestra comprensión de la lógica gráfica de Peirce cambie a medida que aparezcan los 23 volúmenes restantes de la edición cronológica.