Función mayoritaria

En la lógica booleana , la función mayoritaria (también llamada operador mediano ) es la función booleana que se evalúa como falsa cuando la mitad o más de los argumentos son falsos y verdadera en caso contrario, es decir, el valor de la función es igual al valor de la mayoría de las entradas.

Circuitos booleanos

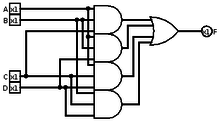
Una puerta mayoritaria es una puerta lógica que se utiliza en la complejidad de circuitos y otras aplicaciones de circuitos booleanos . Una puerta mayoritaria devuelve verdadero si y solo si más del 50 % de sus entradas son verdaderas.

Por ejemplo, en un sumador completo , la salida de acarreo se obtiene aplicando una función mayoritaria a las tres entradas, aunque con frecuencia esta parte del sumador se divide en varias puertas lógicas más simples.

Muchos sistemas tienen redundancia modular triple ; utilizan la función mayoritaria para la decodificación de la lógica mayoritaria para implementar la corrección de errores .

Un resultado importante en la complejidad del circuito afirma que la función mayoritaria no puede calcularse mediante circuitos AC0 de tamaño subexponencial.

Propiedades

Para cualquier x , y , z , el operador mediano ternario ⟨ x , y , z ⟩ satisface las siguientes ecuaciones.

⟨ x , y , y ⟩ = y
⟨ x , y , z ⟩ = ⟨ z , x , y ⟩
⟨ x , y , z ⟩ = ⟨ x , z , y ⟩
⟨⟨ x , w , y ⟩, w , z ⟩ = ⟨ x , w , ⟨ y , w , z ⟩⟩

Un sistema abstracto que satisface estos axiomas es un álgebra mediana .

Corbatas

La mayoría de las aplicaciones fuerzan deliberadamente un número impar de entradas para no tener que lidiar con la cuestión de qué sucede cuando exactamente la mitad de las entradas son 0 y exactamente la mitad de las entradas son 1. Los pocos sistemas que calculan la función mayoritaria en un número par de entradas a menudo están sesgados hacia "0" - producen "0" cuando exactamente la mitad de las entradas son 0 - por ejemplo, una puerta de mayoría de 4 entradas tiene una salida 0 solo cuando aparecen dos o más 0 en sus entradas. ^[1] En unos pocos sistemas, el empate se puede romper aleatoriamente. ^[2]

Fórmulas monótonas para la mayoría

Para n = 1, el operador de mediana es simplemente la operación de identidad unaria x . Para n = 3, el operador de mediana ternario se puede expresar mediante conjunción y disyunción como xy + yz + zx .

Para un número arbitrario de n existe una fórmula monótona para la mayoría de tamaño O( n ^5,3 ). Esto se demuestra mediante el método probabilístico . Por lo tanto, esta fórmula no es constructiva. ^[3]

Existen enfoques para una fórmula explícita para la mayoría del tamaño del polinomio:

Tomemos la mediana de una red de clasificación , donde cada "cable" de comparación e intercambio es simplemente una compuerta OR y una compuerta AND. La construcción Ajtai – Komlós – Szemerédi (AKS) es un ejemplo.
Combine las salidas de circuitos de mayoría más pequeña. ^[4]
Desaleatorizar la prueba Valiant de una fórmula monótona. ^[5]

Véase también

Notas

^ Peterson, William Wesley; Weldon, EJ (1972). Códigos de corrección de errores . MIT Press. ISBN 9780262160391.
^ Chaouiya, Claudine; Ourrad, Ouerdia; Lima, Ricardo (julio de 2013). "La mayoría manda con desempate aleatorio en redes reguladoras de genes booleanos". PLOS ONE . 8 (7). Biblioteca Pública de Ciencias: e69626. Bibcode :2013PLoSO...869626C. doi : 10.1371/journal.pone.0069626 . PMC 3724945 . PMID 23922761.
^ Valiant, Leslie (1984). "Fórmulas monótonas cortas para la función mayoritaria". Journal of Algorithms . 5 (3): 363–366. doi :10.1016/0196-6774(84)90016-6.
^ Amano, Kazuyuki (2018). "Circuitos de mayoría en profundidad para expansores de mayoría y de lista". 43.° Simposio Internacional sobre Fundamentos Matemáticos de la Informática (MFCS 2018) . 117 (81). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: 1–13. doi : 10.4230/LIPIcs.MFCS.2018.81 .
^ Hoory, Shlomo; Magen, Avner; Pitassi, Toniann (2006). "Circuitos monótonos para la función mayoritaria". Aproximación, aleatorización y optimización combinatoria. Algoritmos y técnicas . Apuntes de clase en informática. Vol. 4110. Springer. págs. 410–425. doi :10.1007/11830924_38. ISBN. 978-3-540-38044-3.

Referencias

Knuth, Donald E. (2008). Introducción a los algoritmos combinatorios y funciones booleanas . El arte de la programación informática . Vol. 4a. Upper Saddle River, NJ: Addison-Wesley. págs. 64–74. ISBN 978-0-321-53496-5.

Enlaces externos

Medios relacionados con Funciones de la mayoría en Wikimedia Commons