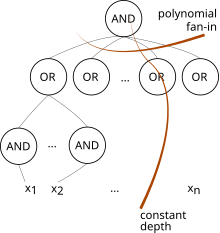
AC 0 es una clase de complejidad utilizada en la complejidad de circuitos . Es la clase más pequeña en la jerarquía AC y consta de todas las familias de circuitos de profundidad O(1) y tamaño polinomial, con puertas AND y puertas OR de fanin ilimitado (permitimos puertas NOT solo en las entradas). [1] Por lo tanto, contiene NC , que solo tiene puertas AND y OR de fanin acotadas. [1]
La suma y resta de enteros se pueden calcular en AC 0 , [2], pero la multiplicación no (específicamente, cuando las entradas son dos enteros bajo las representaciones binarias [3] o de base 10 habituales de enteros).
Dado que es una clase de circuito, como P/poly , AC 0 también contiene todos los lenguajes unarios .
Desde un punto de vista de complejidad descriptiva , DLOGTIME - AC uniforme 0 es igual a la clase descriptiva FO +BIT de todos los lenguajes descriptibles en lógica de primer orden con la adición del predicado BIT , o alternativamente por FO(+, ×), o por la máquina de Turing en la jerarquía logarítmica . [4]
En 1984, Furst, Saxe y Sipser demostraron que el cálculo de la paridad de los bits de entrada (a diferencia de los problemas de suma/resta mencionados anteriormente que tenían dos entradas) no puede decidirse por ningún circuito AC 0 , incluso con no uniformidad. [5] [1] De ello se deduce que AC 0 no es igual a NC 1 , porque una familia de circuitos de la última clase puede calcular la paridad. [1] Se desprenden límites más precisos del lema de conmutación . Utilizándolos, se ha demostrado que existe una separación de oráculo entre la jerarquía polinómica y PSPACE .