El cálculo de varillas o cálculo de varillas fue el método mecánico de cálculo algorítmico con varillas de conteo en China desde los Estados Combatientes hasta la dinastía Ming antes de que las varillas de conteo fueran reemplazadas cada vez más por el ábaco, más conveniente y rápido . El cálculo de varillas jugó un papel clave en el desarrollo de las matemáticas chinas hasta su apogeo en las dinastías Song y Yuan , culminando con la invención de ecuaciones polinómicas de hasta cuatro incógnitas en el trabajo de Zhu Shijie .


El equipo básico para realizar el cálculo con varillas es un conjunto de varillas contadoras y una tabla de contar. Las varillas de conteo suelen estar hechas de varas de bambú, de unos 12 a 15 cm de largo y de 2 a 4 mm de diámetro, a veces de huesos de animales, o de marfil y jade (para los comerciantes adinerados). Un tablero para contar puede ser un tablero de mesa, una tabla de madera con o sin rejilla, en el suelo o sobre arena.
En 1971, arqueólogos chinos desenterraron un paquete de varillas para contar huesos de animales bien conservadas almacenadas en una bolsa de seda de una tumba en el condado de Qian Yang en la provincia de Shanxi, que data de la primera mitad de la dinastía Han (206 a. C. - 8 d. C.). [ cita necesaria ] En 1975 se desenterró un haz de varillas de contar de bambú. [ cita necesaria ]
El uso de varillas de conteo para el cálculo de varillas floreció en los Estados Combatientes , aunque no se encontraron artefactos arqueológicos antes de la dinastía Han Occidental (la primera mitad de la dinastía Han ; sin embargo, los arqueólogos sí desenterraron artefactos de software de cálculo de varillas que databan de los Estados Combatientes). ); Dado que el software de cálculo con varillas debe haber ido junto con el hardware de cálculo con varillas, no hay duda de que el cálculo con varillas ya estaba floreciendo durante los Estados Combatientes hace más de 2.200 años.
El software clave necesario para el cálculo de barras era una sencilla tabla de multiplicar decimal posicional de 45 frases utilizada en China desde la antigüedad, llamada tabla nueve-nueve , que aprendían de memoria alumnos, comerciantes, funcionarios gubernamentales y matemáticos por igual.
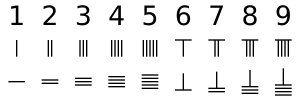

Los números de varilla son el único sistema numérico que utiliza una combinación de ubicación diferente de un solo símbolo para transmitir cualquier número o fracción en el sistema decimal. Para los números en el lugar de las unidades, cada barra vertical representa 1. Dos barras verticales representan 2, y así sucesivamente, hasta 5 barras verticales, que representan 5. Para números entre 6 y 9, se utiliza un sistema biquinario , en el que una barra horizontal en la parte superior de las barras verticales representan 5. La primera fila son los números del 1 al 9 en números de barra, y la segunda fila son los mismos números en forma horizontal.
Para números mayores que 9, se utiliza un sistema decimal . Las varillas colocadas un lugar a la izquierda del lugar de las unidades representan 10 veces ese número. Para el lugar de las centenas, se coloca otro conjunto de varillas a la izquierda que representa 100 veces ese número, y así sucesivamente. Como se muestra en la imagen adyacente, el número 231 está representado en números de barra en la fila superior, con una barra en el lugar de las unidades que representa 1, tres barras en el lugar de las decenas que representan 30 y dos barras en el lugar de las centenas que representan 200, con una suma de 231.
Al realizar los cálculos, normalmente no había ninguna cuadrícula en la superficie. Si los números de varilla dos, tres y uno se colocan consecutivamente en forma vertical, existe la posibilidad de que se confundan con 51 o 24, como se muestra en la segunda y tercera fila de la imagen adyacente. Para evitar confusión, los números en lugares consecutivos se colocan alternando de forma vertical y horizontal, con las unidades colocadas en forma vertical, [1] como se muestra en la fila inferior a la derecha.

En los números de varilla , los ceros están representados por un espacio, que sirve tanto como número como como valor marcador de posición. A diferencia de los números hindú-árabes , no existe un símbolo específico para representar el cero. Antes de la introducción de un cero escrito, además de un espacio para indicar que no hay unidades, el carácter en la siguiente columna de unidades se rotaría 90°, para reducir la ambigüedad de un solo cero. [2] Por ejemplo, 107 (𝍠 𝍧) y 17 (𝍩𝍧) se distinguirían por la rotación, además del espacio, aunque múltiples unidades cero podrían generar ambigüedad, por ejemplo. 1007 (𝍩 𝍧) y 10007 (𝍠 𝍧). En la imagen adyacente, el número cero se representa simplemente con un espacio.
Los matemáticos Song usaban el rojo para representar números positivos y el negro para números negativos . Sin embargo, otra forma es agregar una barra al último lugar para mostrar que el número es negativo. [3]
El Tratado de Matemáticas de Sunzi utilizó metrología de fracciones decimales. La unidad de longitud fue 1 chi ,
1 chi = 10 cun , 1 cun = 10 fen , 1 fen = 10 li , 1 li = 10 hao , 10 hao = 1 shi, 1 shi = 10 hu .
1 chi 2 cun 3 fen 4 li 5 hao 6 shi 7 hu se colocan en el tablero de conteo como
¿Dónde está la unidad de medida chi ?
El matemático de la dinastía Song del Sur, Qin Jiushao, extendió el uso de la fracción decimal más allá de la metrología. En su libro Tratado matemático en nueve secciones , expresó formalmente 1,1446154 días como
Marcó la unidad con la palabra “日” (día) debajo. [4]
El cálculo de varillas funciona según el principio de la suma. A diferencia de los números arábigos , los dígitos representados por varillas contadoras tienen propiedades aditivas. El proceso de suma implica mover mecánicamente las varillas sin necesidad de memorizar una tabla de suma . Esta es la mayor diferencia con los números arábigos, ya que no se pueden juntar mecánicamente 1 y 2 para formar 3, o 2 y 3 juntos para formar 5.
La imagen adyacente presenta los pasos para sumar 3748 a 289:
Las varillas del sumando cambian a lo largo de la suma, mientras que las varillas del sumando en la parte inferior "desaparecen".

En una situación en la que no es necesario pedir prestado , solo es necesario tomar del minuendo el número de barras en el sustraendo . El resultado del cálculo es la diferencia. La imagen adyacente muestra los pasos para restar 23 de 54.
En situaciones en las que se necesita un préstamo, como en el caso del 4231–789, es necesario utilizar un procedimiento más complicado. Los pasos para este ejemplo se muestran a la izquierda.
Sunzi Suanjing describió en detalle el algoritmo de multiplicación. A la izquierda están los pasos para calcular 38×76:
La animación de la izquierda muestra los pasos para calcular309/7= 441/7.
El algoritmo Sunzi para la división fue transmitido íntegramente por al Khwarizmi al país islámico desde fuentes indias en el año 825 d.C. El libro de Al Khwarizmi fue traducido al latín en el siglo XIII. El algoritmo de división Sunzi evolucionó más tarde hasta convertirse en la división de galeras en Europa. El algoritmo de división en el libro de Abu'l-Hasan al-Uqlidisi del año 925 d.C. Kitab al-Fusul fi al-Hisab al-Hindi y en los Principios del cálculo hindú de Kushyar ibn Labban del siglo XI eran idénticos al algoritmo de división de Sunzu.

Si hay un resto en una división de cálculo de varilla decimal con valor posicional, tanto el resto como el divisor deben dejarse en su lugar, uno encima del otro. En las notas de Liu Hui a Jiuzhang suanshu (siglo II a. C.), el número de arriba se llama "shi" (实), mientras que el de abajo se llama "fa" (法). En Sunzi Suanjing , el número de arriba se llama "zi" (子) o "fenzi" (lit., hijo de fracción), y el de abajo se llama "mu" (母) o "fenmu" (lit. , madre de fracción). Fenzi y Fenmu son también el nombre chino moderno para numerador y denominador , respectivamente. Como se muestra a la derecha, 1 es el resto del numerador, 7 es el divisor del denominador, formó una fracción1/7. El cociente de la división.309/7es 44 +1/7. Liu Hui utilizó muchos cálculos con fracciones en Haidao Suanjing .
Esta forma de fracción con numerador arriba y denominador abajo sin una barra horizontal en el medio, fue transmitida al país árabe en un libro del año 825 d.C. por al Khwarizmi a través de la India, y en uso en el siglo X Abu'l-Hasan al-Uqlidisi y en el siglo XV. Siglo obra de Jamshīd al-Kāshī "Clave arithemática".
1/3+2/5
8/9−1/5
31/3× 52/5
El algoritmo para encontrar el máximo común divisor de dos números y la reducción de fracciones se estableció en Jiuzhang suanshu . El máximo común divisor se encuentra mediante divisiones sucesivas con restos hasta que los dos últimos restos sean idénticos. La animación de la derecha ilustra el algoritmo para encontrar el máximo común divisor de32.450.625/59.056.400y reducción de una fracción.
En este caso el hcf es 25.
Divide el numerador y el denominador entre 25. La fracción reducida es1.298.025/2.362.256.
El calendario y matemático He Chengtian (何承天) utilizó el método de interpolación de fracciones , llamado "armonización del divisor del día" (调日法) para obtener un valor aproximado mejor que el anterior sumando iterativamente los numeradores y denominadores de una fracción "más débil". con una "fracción más fuerte". [5] El legendario π = de Zu Chongzhi355/113podría obtenerse con el método de He Chengtian [6]
El capítulo ocho Matrices rectangulares de Jiuzhang suanshu proporcionó un algoritmo para resolver sistemas de ecuaciones lineales mediante el método de eliminación : [7]
Problema 8-1: Supongamos que tenemos 3 paquetes de cereales de alta calidad, 2 paquetes de cereales de calidad media y un paquete de cereales de baja calidad con un peso acumulado de 39 dou. Disponemos también de 2, 3 y 1 paquete de cereales respectivos por valor de 34 dou; También disponemos de 1, 2 y 3 paquetes de cereales respectivos, por un total de 26 dou.
Encuentre la cantidad de cereales de calidad alta, media y mala. En álgebra, este problema se puede expresar en tres sistemas de ecuaciones con tres incógnitas.
Este problema se resolvió en Jiuzhang suanshu con varillas de conteo dispuestas sobre un tablero de conteo en un formato tabular similar a una matriz de 3x4:
Algoritmo:
La cantidad de un paquete de cereal de baja calidad.
De donde se puede obtener fácilmente la cantidad de un paquete de cereales de calidad alta y media:
El algoritmo para la extracción de la raíz cuadrada se describió en Jiuzhang suanshu y con pequeñas diferencias en la terminología en Sunzi Suanjing .
La animación muestra el algoritmo para la extracción del cálculo de barras de una aproximación de la raíz cuadrada del algoritmo del capítulo 2, problema 19 de Sunzi Suanjing:
El algoritmo es como sigue:
.
El matemático de la dinastía Song del Norte, Jia Xian, desarrolló un algoritmo multiplicativo aditivo para la extracción de raíces cuadradas , en el que reemplazó la tradicional "duplicación" de "fang fa" agregando el dígito shang al dígito de fang fa , con el mismo efecto.
Jiuzhang suanshu vol iv "shaoguang" proporcionó un algoritmo para la extracción de raíz cúbica.
〔一九〕今有積一百八十六萬八百六十七尺。問為立方幾何?答曰:一百二十三尺。
problema 19: Tenemos un chi cúbico de 1860867, ¿cuál es la longitud de un lado? Respuesta: 123 chi.
El matemático de la dinastía Song del Norte, Jia Xian, inventó un método similar a la forma simplificada del esquema de Horner para la extracción de raíces cúbicas. La animación de la derecha muestra el algoritmo de Jia Xian para resolver el problema 19 en Jiuzhang suanshu vol 4.
El matemático de la dinastía Song del Norte, Jia Xian, inventó el esquema de Horner para resolver una ecuación simple de cuarto orden de la forma
El matemático de la dinastía Song del Sur, Qin Jiushao, mejoró el método Horner de Jia Xian para resolver ecuaciones polinomiales hasta el décimo orden. El siguiente es el algoritmo para resolver
Esta ecuación se dispuso de abajo hacia arriba con varillas de conteo en un tablero de conteo en forma de tabla.
Algoritmo:

El matemático de la dinastía Yuan, Li Zhi, desarrolló el cálculo de varillas en Tian yuan shu
Ejemplo Li Zhi Ceyuan haijing vol II, problema 14 ecuación de una incógnita:

El matemático Zhu Shijie desarrolló aún más el cálculo de barras para incluir ecuaciones polinómicas de 2 a cuatro incógnitas.
Por ejemplo, polinomios de tres incógnitas:
Ecuación 1:
Ecuación 2:
Ecuación 3:
Después de la eliminación sucesiva de dos incógnitas, las ecuaciones polinómicas de tres incógnitas se redujeron a una ecuación polinómica de una incógnita:
Resuelto x=5;
Lo cual ignora otras 3 respuestas, 2 se repiten.