Prueba de hipótesis estadística

Método de inferencia estadística

La imagen de arriba muestra una tabla con algunas de las estadísticas de prueba más comunes y sus pruebas o modelos correspondientes.

Una prueba de hipótesis estadística es un método de inferencia estadística que se utiliza para decidir si los datos respaldan suficientemente una hipótesis en particular. Una prueba de hipótesis estadística generalmente implica el cálculo de una estadística de prueba . Luego se toma una decisión, ya sea comparando la estadística de prueba con un valor crítico o, equivalentemente, evaluando un valor p calculado a partir de la estadística de prueba. Se han definido aproximadamente 100 pruebas estadísticas especializadas . ^{[1] [2]}

Historia

Si bien las pruebas de hipótesis se popularizaron a principios del siglo XX, las primeras formas de uso se utilizaron en el siglo XVIII. El primer uso se atribuye a John Arbuthnot (1710), ^[3] seguido por Pierre-Simon Laplace (década de 1770), al analizar la proporción de sexos humanos al nacer; consulte § Proporción de sexos humanos.

Elección de la hipótesis nula

Paul Meehl ha sostenido que la importancia epistemológica de la elección de la hipótesis nula ha pasado en gran medida desapercibida. Cuando la hipótesis nula es predicha por la teoría, un experimento más preciso será una prueba más rigurosa de la teoría subyacente. Cuando la hipótesis nula por defecto es "ninguna diferencia" o "ningún efecto", un experimento más preciso es una prueba menos rigurosa de la teoría que motivó la realización del experimento. ^[4] Por lo tanto, puede ser útil examinar los orígenes de esta última práctica:

1778: Pierre Laplace compara las tasas de natalidad de niños y niñas en varias ciudades europeas. Afirma: "es natural concluir que estas posibilidades están casi en la misma proporción". Por lo tanto, la hipótesis nula en este caso es que las tasas de natalidad de niños y niñas deberían ser iguales según la "sabiduría convencional". ^[5]

1900: Karl Pearson desarrolla la prueba de chi cuadrado para determinar "si una forma dada de curva de frecuencia describirá efectivamente las muestras extraídas de una población dada". Por lo tanto, la hipótesis nula es que una población se describe mediante alguna distribución predicha por la teoría. Utiliza como ejemplo los números cinco y seis en los datos del lanzamiento de dados de Weldon . ^[6]

1904: Karl Pearson desarrolla el concepto de " contingencia " para determinar si los resultados son independientes de un factor categórico dado. En este caso, la hipótesis nula es por defecto que dos cosas no están relacionadas (por ejemplo, la formación de cicatrices y las tasas de mortalidad por viruela). ^[7] La ​​hipótesis nula en este caso ya no es predicha por la teoría o la sabiduría convencional, sino que es el principio de indiferencia que llevó a Fisher y a otros a descartar el uso de "probabilidades inversas". ^[8]

Orígenes modernos y controversias tempranas

Las pruebas de significación modernas son en gran parte producto de Karl Pearson ( valor p , prueba de chi-cuadrado de Pearson ), William Sealy Gosset ( distribución t de Student ) y Ronald Fisher (" hipótesis nula ", análisis de varianza , " prueba de significación "), mientras que las pruebas de hipótesis fueron desarrolladas por Jerzy Neyman y Egon Pearson (hijo de Karl). Ronald Fisher comenzó su vida en estadística como bayesiano (Zabell 1992), pero pronto se desilusionó con la subjetividad involucrada (a saber, el uso del principio de indiferencia al determinar probabilidades previas) y buscó proporcionar un enfoque más "objetivo" a la inferencia inductiva. ^[9]

Fisher hizo hincapié en el diseño y los métodos experimentales rigurosos para extraer un resultado de unas pocas muestras asumiendo distribuciones gaussianas . Neyman (que hizo equipo con el joven Pearson) hizo hincapié en el rigor matemático y los métodos para obtener más resultados de muchas muestras y una gama más amplia de distribuciones. Las pruebas de hipótesis modernas son un híbrido inconsistente de la formulación, los métodos y la terminología de Fisher vs. Neyman/Pearson desarrollados a principios del siglo XX.

Fisher popularizó la "prueba de significación". Exigía una hipótesis nula (que correspondía a una distribución de frecuencias de la población) y una muestra. Sus cálculos (que ahora nos resultan familiares) determinaban si se debía rechazar o no la hipótesis nula. La prueba de significación no utilizaba una hipótesis alternativa, por lo que no existía el concepto de error de tipo II (falso negativo).

El valor p fue concebido como un índice informal, pero objetivo, destinado a ayudar a un investigador a determinar (basándose en otro conocimiento) si modificar experimentos futuros o fortalecer su fe en la hipótesis nula. ^[10] La prueba de hipótesis (y errores de tipo I/II) fue concebida por Neyman y Pearson como una alternativa más objetiva al valor p de Fisher , también destinada a determinar el comportamiento del investigador, pero sin requerir ninguna inferencia inductiva por parte del investigador. ^{[11] [12]}

Neyman y Pearson consideraron un problema diferente al de Fisher (al que llamaron "prueba de hipótesis"). Inicialmente, consideraron dos hipótesis simples (ambas con distribuciones de frecuencia). Calcularon dos probabilidades y, por lo general, seleccionaron la hipótesis asociada con la probabilidad más alta (la hipótesis con mayor probabilidad de haber generado la muestra). Su método siempre seleccionaba una hipótesis. También permitía el cálculo de ambos tipos de probabilidades de error.

Fisher y Neyman/Pearson chocaron duramente. Neyman/Pearson consideraban que su formulación era una generalización mejorada de las pruebas de significación (el artículo definitorio ^[11] era abstracto ; los matemáticos han generalizado y refinado la teoría durante décadas ^[13] ). Fisher pensaba que no era aplicable a la investigación científica porque a menudo, durante el curso del experimento, se descubre que las suposiciones iniciales sobre la hipótesis nula son cuestionables debido a fuentes inesperadas de error. Creía que el uso de decisiones rígidas de rechazar/aceptar basadas en modelos formulados antes de que se recopilen los datos era incompatible con este escenario común al que se enfrentan los científicos y que los intentos de aplicar este método a la investigación científica conducirían a una confusión masiva. ^[14]

La disputa entre Fisher y Neyman-Pearson se libró sobre bases filosóficas, y un filósofo la caracterizó como una disputa sobre el papel apropiado de los modelos en la inferencia estadística. ^[15]

Los acontecimientos intervinieron: Neyman aceptó un puesto en la Universidad de California, Berkeley en 1938, rompiendo su asociación con Pearson y separando a los contendientes (que habían ocupado el mismo edificio). La Segunda Guerra Mundial proporcionó un intermedio en el debate. La disputa entre Fisher y Neyman terminó (sin resolverse después de 27 años) con la muerte de Fisher en 1962. Neyman escribió un panegírico muy bien considerado. ^[16] Algunas de las publicaciones posteriores de Neyman informaron valores p y niveles de significación. ^[17]

La versión moderna de la prueba de hipótesis es un híbrido de los dos enfoques que resultaron de la confusión de los escritores de libros de texto estadísticos (como predijo Fisher) a partir de la década de 1940 ^[18] (pero la detección de señales , por ejemplo, todavía utiliza la formulación de Neyman/Pearson). Se ignoraron grandes diferencias conceptuales y muchas salvedades además de las mencionadas anteriormente. Neyman y Pearson proporcionaron la terminología más sólida, las matemáticas más rigurosas y la filosofía más consistente, pero el tema que se enseña hoy en estadística introductoria tiene más similitudes con el método de Fisher que con el de ellos. ^[19]

En algún momento alrededor de 1940, ^[18] los autores de libros de texto estadísticos comenzaron a combinar los dos enfoques utilizando el valor p en lugar de la estadística de prueba (o datos) para probar contra el "nivel de significancia" de Neyman-Pearson.

Filosofía

La prueba de hipótesis y la filosofía se entrecruzan. La estadística inferencial , que incluye la prueba de hipótesis, es probabilidad aplicada. Tanto la probabilidad como su aplicación están entrelazadas con la filosofía. El filósofo David Hume escribió: "Todo conocimiento degenera en probabilidad". Las definiciones prácticas en pugna de la probabilidad reflejan diferencias filosóficas. La aplicación más común de la prueba de hipótesis es la interpretación científica de datos experimentales, que naturalmente se estudia mediante la filosofía de la ciencia .

Fisher y Neyman se opusieron a la subjetividad de la probabilidad. Sus opiniones contribuyeron a las definiciones objetivas. El núcleo de su desacuerdo histórico era filosófico.

Los estadísticos discuten muchas de las críticas filosóficas a las pruebas de hipótesis en otros contextos, en particular la de que la correlación no implica causalidad y la del diseño de experimentos . Las pruebas de hipótesis siguen siendo de interés para los filósofos. ^{[15] [20]}

Educación

Cada vez se enseña más estadística en las escuelas, y la prueba de hipótesis es uno de los elementos que se enseñan. ^{[21] [22]} Muchas conclusiones publicadas en la prensa popular (desde encuestas de opinión política hasta estudios médicos) se basan en estadísticas. Algunos autores han afirmado que el análisis estadístico de este tipo permite pensar con claridad sobre problemas que involucran datos masivos, así como la presentación efectiva de tendencias e inferencias a partir de dichos datos, pero advierten que los escritores para un público amplio deben tener un conocimiento sólido del campo para usar los términos y conceptos correctamente. ^{[23] [24]} Una clase introductoria de estadística universitaria pone mucho énfasis en la prueba de hipótesis, tal vez la mitad del curso. Campos como la literatura y la teología ahora incluyen hallazgos basados ​​en el análisis estadístico (ver el Analizador de la Biblia ). Una clase introductoria de estadística enseña la prueba de hipótesis como un proceso de libro de cocina. La prueba de hipótesis también se enseña a nivel de posgrado. Los estadísticos aprenden cómo crear buenos procedimientos de prueba estadística (como z , t de Student , F y chi-cuadrado). La prueba de hipótesis estadísticas se considera un área madura dentro de la estadística, ^[25] pero aún se encuentra en desarrollo de forma limitada.

Un estudio académico afirma que el método de libro de cocina para enseñar estadística introductoria no deja tiempo para la historia, la filosofía o la controversia. La prueba de hipótesis se ha enseñado como un método unificado aceptado. Las encuestas mostraron que los graduados de la clase estaban llenos de conceptos erróneos filosóficos (sobre todos los aspectos de la inferencia estadística) que persistían entre los instructores. ^[26] Si bien el problema se abordó hace más de una década, ^[27] y los llamados a la reforma educativa continúan, ^[28] los estudiantes aún se gradúan de las clases de estadística con conceptos erróneos fundamentales sobre la prueba de hipótesis. ^[29] Las ideas para mejorar la enseñanza de la prueba de hipótesis incluyen alentar a los estudiantes a buscar errores estadísticos en artículos publicados, enseñar la historia de la estadística y enfatizar la controversia en un tema generalmente árido. ^[30]

Realización de una prueba de hipótesis frecuentista en la práctica

Los pasos típicos implicados en la realización de una prueba de hipótesis frecuentista en la práctica son:

1. Definir una hipótesis (afirmación que se puede comprobar utilizando datos).
2. Seleccione una prueba estadística relevante con la estadística de prueba asociada T.
3. Derive la distribución del estadístico de prueba bajo la hipótesis nula a partir de los supuestos. En casos estándar, este será un resultado bien conocido. Por ejemplo, el estadístico de prueba podría seguir una distribución t de Student con grados de libertad conocidos, o una distribución normal con media y varianza conocidas.
4. Seleccione un nivel de significancia ( α ), la tasa máxima aceptable de falsos positivos . Los valores comunes son 5% y 1%.
5. Calcular a partir de las observaciones el valor observado t _obs del estadístico de prueba T.
6. Decide si rechazar la hipótesis nula a favor de la alternativa o no rechazarla. La regla de decisión de Neyman-Pearson es rechazar la hipótesis nula H ₀ si el valor observado t _obs está en la región crítica y no rechazar la hipótesis nula en caso contrario. ^[31]

Ejemplo práctico

La diferencia entre los dos procesos aplicados al ejemplo de la maleta radiactiva (abajo):

• "La lectura del contador Geiger es 10. El límite es 9. Revise la maleta".
• "La lectura del contador Geiger es alta; el 97% de las maletas seguras tienen lecturas más bajas. El límite es el 95%. Revise la maleta".

El primer informe es adecuado, el segundo da una explicación más detallada de los datos y el motivo por el cual se revisa la maleta.

No rechazar la hipótesis nula no significa que la hipótesis nula sea "aceptada" per se (aunque Neyman y Pearson usaron esa palabra en sus escritos originales; ver la sección Interpretación).

Los procesos descritos aquí son perfectamente adecuados para el cálculo, pero descuidan seriamente las consideraciones sobre el diseño de experimentos . ^{[32] [33]}

Es especialmente importante estimar tamaños de muestra adecuados antes de realizar el experimento.

La frase "prueba de significación" fue acuñada por el estadístico Ronald Fisher . ^[34]

Interpretación

Cuando la hipótesis nula es verdadera y se cumplen los supuestos estadísticos, la probabilidad de que el valor p sea menor o igual al nivel de significancia es como máximo . Esto garantiza que la prueba de hipótesis mantenga su tasa de falsos positivos especificada (siempre que se cumplan los supuestos estadísticos). ^[35] ${\displaystyle \alpha }$ ${\displaystyle \alpha }$

El valor p es la probabilidad de que se dé un estadístico de prueba que sea al menos tan extremo como el obtenido bajo la hipótesis nula. Con un nivel de significación de 0,05, se esperaría que una moneda justa rechazara (incorrectamente) la hipótesis nula (que es justa) en 1 de cada 20 pruebas en promedio. El valor p no proporciona la probabilidad de que la hipótesis nula o su opuesta sean correctas (una fuente común de confusión). ^[36]

Si el valor p es menor que el umbral de significancia elegido (equivalentemente, si la estadística de prueba observada está en la región crítica), entonces decimos que la hipótesis nula se rechaza en el nivel de significancia elegido. Si el valor p no es menor que el umbral de significancia elegido (equivalentemente, si la estadística de prueba observada está fuera de la región crítica), entonces la hipótesis nula no se rechaza en el nivel de significancia elegido.

En el ejemplo de la "señora que prueba el té" (abajo), Fisher le pidió a la señora que clasificara correctamente todas las tazas de té para justificar la conclusión de que era poco probable que el resultado fuera fruto del azar. Su prueba reveló que si la señora estaba adivinando al azar (la hipótesis nula), había una probabilidad del 1,4 % de que se produjeran los resultados observados (té perfectamente ordenado).

Uso e importancia

Las estadísticas son útiles para analizar la mayoría de los conjuntos de datos. Esto es igualmente cierto en el caso de las pruebas de hipótesis, que pueden justificar conclusiones incluso cuando no existe una teoría científica. En el ejemplo de la señora que degustaba té, era "obvio" que no existía diferencia entre (leche vertida en té) y (té vertido en leche). Los datos contradecían lo "obvio".

Las aplicaciones en el mundo real de las pruebas de hipótesis incluyen: ^[37]

• Investigadores descubren si los hombres sufren más pesadillas que las mujeres
• Establecimiento de la autoría de los documentos
• Evaluación del efecto de la luna llena sobre el comportamiento
• Determinar el alcance al que un murciélago puede detectar un insecto mediante eco
• Decidir si las alfombras de los hospitales provocan más infecciones
• Seleccionar los mejores medios para dejar de fumar
• Cómo comprobar si las pegatinas para el parachoques reflejan el comportamiento del propietario del vehículo
• Poniendo a prueba las afirmaciones de los analistas de escritura a mano

La comprobación de hipótesis estadísticas desempeña un papel importante en toda la estadística y en la inferencia estadística . Por ejemplo, Lehmann (1992), en una revisión del artículo fundamental de Neyman y Pearson (1933), dice: "Sin embargo, a pesar de sus deficiencias, el nuevo paradigma formulado en el artículo de 1933 y los numerosos desarrollos realizados dentro de su marco siguen desempeñando un papel central tanto en la teoría como en la práctica de la estadística y se puede esperar que lo sigan haciendo en el futuro previsible".

Las pruebas de significancia han sido la herramienta estadística favorita en algunas ciencias sociales experimentales (más del 90% de los artículos en el Journal of Applied Psychology durante la década de 1990). ^[38] Otros campos han favorecido la estimación de parámetros (por ejemplo, el tamaño del efecto ). Las pruebas de significancia se utilizan como un sustituto de la comparación tradicional del valor predicho y el resultado experimental en el núcleo del método científico . Cuando la teoría solo es capaz de predecir el signo de una relación, se puede configurar una prueba de hipótesis direccional (unilateral) de modo que solo un resultado estadísticamente significativo respalde la teoría. Esta forma de evaluación de la teoría es la aplicación más criticada de las pruebas de hipótesis.

Precauciones

"Si el gobierno exigiera que los procedimientos estadísticos llevaran etiquetas de advertencia como las de los medicamentos, la mayoría de los métodos de inferencia tendrían, de hecho, etiquetas largas". ^[39] Esta advertencia se aplica a las pruebas de hipótesis y a las alternativas a ellas.

La prueba de hipótesis exitosa está asociada con una probabilidad y una tasa de error tipo I. La conclusión podría ser errónea.

La conclusión de la prueba es tan sólida como la muestra en la que se basa. El diseño del experimento es fundamental. Se han observado varios efectos inesperados, entre ellos:

• El ingenioso efecto Hans . Un caballo parecía ser capaz de realizar operaciones aritméticas sencillas.
• El efecto Hawthorne . Los trabajadores industriales eran más productivos con mejor iluminación y más productivos con peor iluminación.
• El efecto placebo . Las pastillas sin ingredientes activos desde el punto de vista médico resultaron notablemente eficaces.

Un análisis estadístico de datos engañosos produce conclusiones engañosas. La cuestión de la calidad de los datos puede ser más sutil. En la previsión , por ejemplo, no hay acuerdo sobre una medida de la precisión de las previsiones. En ausencia de una medida de consenso, ninguna decisión basada en mediciones estará libre de controversias.

Sesgo de publicación: Es posible que los resultados estadísticamente no significativos tengan menos probabilidades de publicarse, lo que puede sesgar la literatura.

Pruebas múltiples: cuando se realizan múltiples pruebas de hipótesis nulas verdaderas a la vez sin ajuste, la probabilidad general de error tipo I es mayor que el nivel alfa nominal. ^[40]

Quienes toman decisiones críticas basándose en los resultados de una prueba de hipótesis son prudentes y se fijan en los detalles en lugar de en la conclusión únicamente. En las ciencias físicas, la mayoría de los resultados se aceptan plenamente sólo cuando se confirman de forma independiente. El consejo general en materia de estadística es: "Las cifras nunca mienten, pero los mentirosos calculan" (anónimo).

Definición de términos

Las siguientes definiciones se basan principalmente en la exposición del libro de Lehmann y Romano: ^[35]

• Hipótesis estadística : Una declaración sobre los parámetros que describen una población (no una muestra ).
• Estadística de prueba: Valor calculado a partir de una muestra sin parámetros desconocidos, a menudo para resumir la muestra con fines de comparación.
• Hipótesis simple : Cualquier hipótesis que especifique completamente la distribución de la población.
• Hipótesis compuesta: Cualquier hipótesis que no especifica completamente la distribución de la población.
• Hipótesis nula (H ₀ )
• Datos positivos: Datos que permiten al investigador rechazar una hipótesis nula.
• Hipótesis alternativa (H ₁ )

Supongamos que los datos pueden obtenerse a partir de una distribución N(0,1). Por ejemplo, con un nivel de significancia elegido α = 0,05, de la tabla Z, se puede obtener un valor crítico unilateral de aproximadamente 1,645. El valor crítico unilateral C _α ≈ 1,645 corresponde al nivel de significancia elegido. La región crítica [C _α , ∞) se obtiene como la cola de la distribución normal estándar.

• Los valores críticos de una prueba estadística son los límites de la región de aceptación de la prueba.^[41]La región de aceptación es el conjunto de valores de la estadística de prueba para los cuales no se rechaza la hipótesis nula. Dependiendo de la forma de la región de aceptación, puede haber uno o más valores críticos.
  • Región de rechazo /Región crítica : El conjunto de valores del estadístico de prueba para el cual se rechaza la hipótesis nula.
• Potencia de una prueba (1 −  β )
• Tamaño : Para hipótesis simples, esta es la probabilidad de la prueba de rechazar incorrectamente la hipótesis nula. Latasa de falsos positivos . Para hipótesis compuestas, este es el máximo de la probabilidad de rechazar la hipótesis nula sobre todos los casos cubiertos por la hipótesis nula. El complemento de la tasa de falsos positivos se denomina especificidad en bioestadística . ("Esta es una prueba específica. Debido a que el resultado es positivo, podemos decir con confianza que el paciente tiene la afección"). Consulte sensibilidad y especificidad y errores tipo I y tipo II para obtener definiciones exhaustivas.
• Nivel de significancia de una prueba ( α)
• valor p
• Prueba de significación estadística : predecesora de la prueba de hipótesis estadística (véase la sección Orígenes). Se decía que un resultado experimental eraestadísticamente significativosi una muestra era suficientemente inconsistente con la hipótesis (nula). Esto se consideraba una cuestión de sentido común, una heurística pragmática para identificar resultados experimentales significativos, una convención que establecía un umbral de evidencia estadística o un método para extraer conclusiones de los datos. La prueba de hipótesis estadística agregó rigor matemático y consistencia filosófica al concepto al hacer explícita la hipótesis alternativa. El término se usa de manera vaga para la versión moderna que ahora es parte de las pruebas de hipótesis estadísticas.
• Prueba conservadora: una prueba es conservadora si, cuando se construye para un nivel de significancia nominal dado, la probabilidad real de rechazar incorrectamente la hipótesis nula nunca es mayor que el nivel nominal.
• Prueba exacta

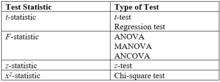
Una prueba de hipótesis estadística compara una estadística de prueba ( z o t , por ejemplo) con un umbral. La estadística de prueba (la fórmula que se encuentra en la tabla siguiente) se basa en la optimalidad. Para un nivel fijo de tasa de error de tipo I, el uso de estas estadísticas minimiza las tasas de error de tipo II (equivalente a maximizar la potencia). Los siguientes términos describen las pruebas en términos de dicha optimalidad:

• Prueba más poderosa: Para un tamaño o nivel de significancia dado , la prueba con mayor potencia (probabilidad de rechazo) para un valor dado del parámetro(s) que se está probando, contenido en la hipótesis alternativa.
• Prueba uniformemente más potente (UMP)

Prueba de hipótesis bootstrap no paramétrica

Los métodos de remuestreo basados ​​en bootstrap se pueden utilizar para probar la hipótesis nula. Un bootstrap crea numerosas muestras simuladas al remuestrear aleatoriamente (con reemplazo) los datos de muestra originales combinados, suponiendo que la hipótesis nula es correcta. El bootstrap es muy versátil, ya que no tiene distribución y no se basa en supuestos paramétricos restrictivos, sino en métodos aproximados empíricos con garantías asintóticas. Las pruebas de hipótesis paramétricas tradicionales son más eficientes computacionalmente pero hacen supuestos estructurales más sólidos. En situaciones en las que calcular la probabilidad de la estadística de prueba bajo la hipótesis nula es difícil o imposible (debido quizás a inconvenientes o falta de conocimiento de la distribución subyacente), el bootstrap ofrece un método viable para la inferencia estadística. ^{[42] [43] [44] [45]}

Ejemplos

Relación sexual humana

El uso más temprano de las pruebas de hipótesis estadísticas se atribuye generalmente a la cuestión de si los nacimientos de hombres y mujeres son igualmente probables (hipótesis nula), que fue abordada en la década de 1700 por John Arbuthnot (1710), ^[46] y más tarde por Pierre-Simon Laplace (década de 1770). ^[47]

Arbuthnot examinó los registros de nacimiento en Londres para cada uno de los 82 años desde 1629 a 1710, y aplicó la prueba de signos , una prueba no paramétrica simple . ^{[48] [49] [50]} En cada año, el número de varones nacidos en Londres superó al número de mujeres. Considerando más nacimientos de varones o más nacimientos de mujeres como igualmente probables, la probabilidad del resultado observado es 0,5 ⁸² , o aproximadamente 1 en 4.836.000.000.000.000.000.000.000; en términos modernos, este es el valor p . Arbuthnot concluyó que esto es demasiado pequeño para deberse al azar y, en cambio, debe deberse a la providencia divina: "De donde se sigue que es el arte, no el azar, lo que gobierna". En términos modernos, rechazó la hipótesis nula de nacimientos de varones y mujeres igualmente probables en el nivel de significación p  = 1/2 ⁸² .

Laplace analizó las estadísticas de casi medio millón de nacimientos y demostró que había un exceso de niños en comparación con las niñas. ^{[5] [51] Mediante el cálculo de un valor} p , concluyó que el exceso era un efecto real, pero inexplicable. ^[52]

Señora degustando té

En un famoso ejemplo de prueba de hipótesis, conocido como la dama que prueba el té , ^[53] la Dra. Muriel Bristol , colega de Fisher, afirmó ser capaz de decir si el té o la leche se agregó primero a una taza. Fisher propuso darle ocho tazas, cuatro de cada variedad, en orden aleatorio. Uno podría entonces preguntar cuál era la probabilidad de que ella obtuviera el número que acertó, pero solo por casualidad. La hipótesis nula fue que la dama no tenía tal capacidad. La estadística de prueba fue un simple recuento del número de éxitos en la selección de las 4 tazas. La región crítica fue el caso único de 4 éxitos de 4 posibles según un criterio de probabilidad convencional (< 5%). Un patrón de 4 éxitos corresponde a 1 de 70 combinaciones posibles (p≈ 1,4%). Fisher afirmó que no se requirió (nunca) ninguna hipótesis alternativa. La dama identificó correctamente cada taza, ^[54] lo que se consideraría un resultado estadísticamente significativo.

Juicio en sala de audiencias

El procedimiento de prueba estadística es comparable a un proceso penal : el acusado es considerado inocente mientras no se demuestre su culpabilidad. El fiscal intenta demostrar la culpabilidad del acusado. Sólo cuando existen pruebas suficientes para la acusación se condena al acusado.

Al inicio del procedimiento, hay dos hipótesis : "el acusado no es culpable" y "el acusado es culpable". La primera, , se llama hipótesis nula . La segunda, , se llama hipótesis alternativa . Es la hipótesis alternativa que se espera sustentar. ${\displaystyle H_{0}}$ ${\displaystyle H_{1}}$ ${\displaystyle H_{0}}$ ${\displaystyle H_{1}}$

La hipótesis de inocencia se rechaza únicamente cuando el error es muy improbable, porque no se desea condenar a un acusado inocente. Este tipo de error se denomina error del primer tipo (es decir, la condena de una persona inocente) y se controla su ocurrencia para que sea poco frecuente. Como consecuencia de este comportamiento asimétrico, es más frecuente un error del segundo tipo (absolver a la persona que cometió el delito).

Un proceso penal puede considerarse como uno o ambos de los dos procesos de decisión: culpable vs. inocente o evidencia vs. un umbral ("más allá de toda duda razonable"). En un punto de vista, se juzga al acusado; en el otro, se juzga el desempeño de la acusación (que soporta la carga de la prueba). Una prueba de hipótesis puede considerarse como un juicio de una hipótesis o como un juicio de evidencia.

Frijoles filosofales

El siguiente ejemplo fue elaborado por un filósofo que describió métodos científicos generaciones antes de que se formalizaran y popularizaran las pruebas de hipótesis. ^[55]

De este puñado, pocas judías son blancas.
La mayoría de las judías de esta bolsa son blancas.
Por lo tanto: Probablemente, estas judías se sacaron de otra bolsa.
Esta es una inferencia hipotética.

Los frijoles en la bolsa son la población. El puñado es la muestra. La hipótesis nula es que la muestra se originó a partir de la población. El criterio para rechazar la hipótesis nula es la diferencia "obvia" en apariencia (una diferencia informal en la media). El resultado interesante es que la consideración de una población real y una muestra real produjo una bolsa imaginaria. El filósofo estaba considerando la lógica en lugar de la probabilidad. Para ser una prueba de hipótesis estadística real, este ejemplo requiere las formalidades de un cálculo de probabilidad y una comparación de esa probabilidad con un estándar.

Una generalización simple del ejemplo considera una bolsa mixta de frijoles y un puñado que contiene muy pocos o muchos frijoles blancos. La generalización considera ambos extremos. Requiere más cálculos y más comparaciones para llegar a una respuesta formal, pero la filosofía central no cambia: si la composición del puñado es muy diferente a la de la bolsa, entonces la muestra probablemente se originó de otra bolsa. El ejemplo original se denomina prueba unilateral o de una cola, mientras que la generalización se denomina prueba bilateral o de dos colas.

La afirmación también se basa en la inferencia de que el muestreo fue aleatorio. Si alguien hubiera estado rebuscando en la bolsa para encontrar frijoles blancos, eso explicaría por qué el puñado tenía tantos frijoles blancos y también explicaría por qué se agotó el número de frijoles blancos en la bolsa (aunque probablemente se suponga que la bolsa es mucho más grande que la mano de uno).

Juego de cartas clarividente

Se realiza una prueba de clarividencia a una persona (el sujeto) . Se le muestra el reverso de una carta elegida al azar 25 veces y se le pregunta a cuál de los cuatro palos pertenece. El número de aciertos, o respuestas correctas, se denomina X.

Mientras tratamos de encontrar evidencia de su clarividencia, por el momento la hipótesis nula es que la persona no es clarividente. ^[56] La alternativa es: la persona es (más o menos) clarividente.

Si la hipótesis nula es válida, lo único que puede hacer el sujeto de prueba es adivinar. Para cada carta, la probabilidad (frecuencia relativa) de que aparezca un solo palo es 1/4. Si la alternativa es válida, el sujeto de prueba predecirá correctamente el palo con una probabilidad mayor que 1/4. Llamaremos a la probabilidad de adivinar correctamente p . Las hipótesis, entonces, son:

• hipótesis nula     (sólo una suposición) ${\displaystyle {\text{:}}\qquad H_{0}:p={\tfrac {1}{4}}}$

y

• hipótesis alternativa    (clarividente verdadero). ${\displaystyle {\text{:}}H_{1}:p>{\tfrac {1}{4}}}$

Si el sujeto de prueba predice correctamente las 25 cartas, lo consideraremos clarividente y rechazaremos la hipótesis nula. Lo mismo ocurre con 24 o 23 aciertos. En cambio, con solo 5 o 6 aciertos no hay motivos para considerarlo así. Pero ¿qué pasa con 12 o 17 aciertos? ¿Cuál es el número crítico, c , de aciertos, en cuyo caso consideramos que el sujeto es clarividente? ¿Cómo determinamos el valor crítico c ? Con la opción c = 25 (es decir, solo aceptamos la clarividencia cuando se predicen correctamente todas las cartas) somos más críticos que con c = 10. En el primer caso, casi ningún sujeto de prueba será reconocido como clarividente, en el segundo caso, un cierto número pasará la prueba. En la práctica, uno decide cuán crítico será, es decir, uno decide con qué frecuencia acepta un error del primer tipo: un falso positivo o error de tipo I. Con c = 25, la probabilidad de tal error es:

${\displaystyle P({\text{reject }}H_{0}\mid H_{0}{\text{ is valid}})=P\left(X=25\mid p={\frac {1}{4}}\right)=\left({\frac {1}{4}}\right)^{25}\approx 10^{-15}}$,

y por lo tanto, muy pequeña. La probabilidad de un falso positivo es la probabilidad de acertar al azar las 25 veces.

Siendo menos crítico, con c = 10, se obtiene:

${\displaystyle P({\text{reject }}H_{0}\mid H_{0}{\text{ is valid}})=P\left(X\geq 10\mid p={\frac {1}{4}}\right)=\sum _{k=10}^{25}P\left(X=k\mid p={\frac {1}{4}}\right)=\sum _{k=10}^{25}{\binom {25}{k}}\left(1-{\frac {1}{4}}\right)^{25-k}\left({\frac {1}{4}}\right)^{k}\approx 0.0713}$.

Por lo tanto, c = 10 produce una probabilidad mucho mayor de falso positivo.

Antes de que se realice la prueba, se determina la probabilidad máxima aceptable de un error de tipo I ( α ). Normalmente, se seleccionan valores en el rango de 1% a 5%. (Si la tasa de error máxima aceptable es cero, se requiere un número infinito de intentos correctos). Dependiendo de esta tasa de error de tipo 1, se calcula el valor crítico c . Por ejemplo, si seleccionamos una tasa de error de 1%, c se calcula de la siguiente manera:

${\displaystyle P({\text{reject }}H_{0}\mid H_{0}{\text{ is valid}})=P\left(X\geq c\mid p={\frac {1}{4}}\right)\leq 0.01}$.

De todos los números c, con esta propiedad, elegimos el más pequeño, para minimizar la probabilidad de un error de tipo II, un falso negativo . Para el ejemplo anterior, seleccionamos: . ${\displaystyle c=13}$

Variaciones y subclases

La prueba de hipótesis estadística es una técnica clave tanto de la inferencia frecuentista como de la inferencia bayesiana , aunque los dos tipos de inferencia tienen diferencias notables. Las pruebas de hipótesis estadísticas definen un procedimiento que controla (corrige) la probabilidad de decidir incorrectamente que una posición predeterminada ( hipótesis nula ) es incorrecta. El procedimiento se basa en la probabilidad de que ocurra un conjunto de observaciones si la hipótesis nula fuera verdadera. Esta probabilidad de tomar una decisión incorrecta no es la probabilidad de que la hipótesis nula sea verdadera, ni de si alguna hipótesis alternativa específica es verdadera. Esto contrasta con otras técnicas posibles de la teoría de la decisión en las que la hipótesis nula y la alternativa se tratan de manera más igualitaria.

Un enfoque bayesiano ingenuo para la prueba de hipótesis es basar las decisiones en la probabilidad posterior , ^{[57] [58]} pero esto falla cuando se comparan hipótesis puntuales y continuas. Otros enfoques para la toma de decisiones, como la teoría de decisión bayesiana , intentan equilibrar las consecuencias de las decisiones incorrectas entre todas las posibilidades, en lugar de concentrarse en una sola hipótesis nula. Hay varios otros enfoques para llegar a una decisión basada en datos disponibles a través de la teoría de decisiones y las decisiones óptimas , algunas de las cuales tienen propiedades deseables. Sin embargo, la prueba de hipótesis es un enfoque dominante para el análisis de datos en muchos campos de la ciencia. Las extensiones de la teoría de la prueba de hipótesis incluyen el estudio del poder de las pruebas, es decir, la probabilidad de rechazar correctamente la hipótesis nula dado que es falsa. Tales consideraciones se pueden utilizar para determinar el tamaño de la muestra antes de la recopilación de datos.

Prueba de hipótesis de Neyman-Pearson

Un ejemplo de prueba de hipótesis de Neyman-Pearson (o prueba de significación estadística de hipótesis nula) se puede hacer modificando el ejemplo de la maleta radiactiva. Si la "maleta" es en realidad un contenedor blindado para el transporte de material radiactivo, entonces se podría utilizar una prueba para seleccionar entre tres hipótesis: ninguna fuente radiactiva presente, una presente, dos (todas) presentes. La prueba podría ser necesaria por razones de seguridad, y en cada caso se requerirían acciones. El lema de Neyman-Pearson de la prueba de hipótesis dice que un buen criterio para la selección de hipótesis es la razón de sus probabilidades (una razón de verosimilitud ). Un método simple de solución es seleccionar la hipótesis con la mayor probabilidad para los conteos Geiger observados. El resultado típico coincide con la intuición: pocos conteos implican que no hay fuente, muchos conteos implican dos fuentes y los conteos intermedios implican una fuente. Observe también que, por lo general, existen problemas para probar una hipótesis negativa . Las hipótesis nulas deben ser, al menos, falsables .

La teoría de Neyman-Pearson puede tener en cuenta tanto las probabilidades previas como los costos de las acciones resultantes de las decisiones. ^[59] La primera permite que cada prueba considere los resultados de pruebas anteriores (a diferencia de las pruebas de significancia de Fisher). La segunda permite considerar cuestiones económicas (por ejemplo) así como probabilidades. Una razón de verosimilitud sigue siendo un buen criterio para seleccionar entre hipótesis.

Las dos formas de prueba de hipótesis se basan en diferentes formulaciones del problema. La prueba original es análoga a una pregunta de verdadero/falso; la prueba de Neyman-Pearson es más parecida a una de opción múltiple. En opinión de Tukey ^[60], la primera produce una conclusión basándose únicamente en evidencia sólida, mientras que la segunda produce una decisión basándose en la evidencia disponible. Si bien las dos pruebas parecen bastante diferentes tanto matemática como filosóficamente, desarrollos posteriores conducen a la afirmación opuesta. Consideremos muchas fuentes radiactivas diminutas. Las hipótesis se convierten en 0, 1, 2, 3... granos de arena radiactiva. Hay poca distinción entre ninguna o algo de radiación (Fisher) y 0 granos de arena radiactiva frente a todas las alternativas (Neyman-Pearson). El importante artículo de Neyman-Pearson de 1933 ^[11] también consideró hipótesis compuestas (aquellas cuya distribución incluye un parámetro desconocido). Un ejemplo demostró la optimalidad de la prueba t (de Student) : "no puede haber una prueba mejor para la hipótesis en cuestión" (p. 321). La teoría de Neyman-Pearson demostró la optimalidad de los métodos fisherianos desde sus inicios.

La prueba de significancia de Fisher ha demostrado ser una herramienta estadística flexible y popular en aplicaciones con poco potencial de crecimiento matemático. La prueba de hipótesis de Neyman-Pearson se considera un pilar de la estadística matemática, ^[61] creando un nuevo paradigma para el campo. También estimuló nuevas aplicaciones en el control de procesos estadísticos , la teoría de detección , la teoría de decisiones y la teoría de juegos . Ambas formulaciones han tenido éxito, pero los éxitos han sido de carácter diferente.

La disputa sobre las formulaciones no se ha resuelto. La ciencia utiliza principalmente la formulación de Fisher (ligeramente modificada) que se enseña en las estadísticas introductorias. Los estadísticos estudian la teoría de Neyman-Pearson en la escuela de posgrado. Los matemáticos se enorgullecen de unificar las formulaciones. Los filósofos las consideran por separado. Las opiniones eruditas consideran que las formulaciones son competitivas (Fisher vs. Neyman), incompatibles ^{[9] o complementarias [13]} . La disputa se ha vuelto más compleja desde que la inferencia bayesiana ha alcanzado respetabilidad.

La terminología es inconsistente. La prueba de hipótesis puede significar cualquier combinación de dos formulaciones que hayan cambiado con el tiempo. Cualquier discusión sobre la prueba de significación versus la prueba de hipótesis es doblemente vulnerable a la confusión.

Fisher pensaba que la prueba de hipótesis era una estrategia útil para realizar un control de calidad industrial, sin embargo, estaba en total desacuerdo con que la prueba de hipótesis pudiera ser útil para los científicos. ^[10] La prueba de hipótesis proporciona un medio para encontrar las estadísticas de prueba utilizadas en las pruebas de significancia. ^[13] El concepto de potencia es útil para explicar las consecuencias de ajustar el nivel de significancia y se utiliza mucho en la determinación del tamaño de la muestra . Los dos métodos siguen siendo filosóficamente distintos. ^[15] Por lo general (pero no siempre ) producen la misma respuesta matemática. La respuesta preferida depende del contexto. ^[13] Si bien la fusión existente de las teorías de Fisher y Neyman-Pearson ha sido muy criticada, se ha considerado modificar la fusión para lograr objetivos bayesianos. ^[62]

Crítica

Las críticas a las pruebas de hipótesis estadísticas llenan volúmenes. ^{[63] [64] [65] [66] [67] [68]} Gran parte de las críticas se pueden resumir en las siguientes cuestiones:

• La interpretación de un valor p depende de la regla de detención y de la definición de comparación múltiple. La primera suele cambiar durante el curso de un estudio y la segunda es inevitablemente ambigua (es decir, "los valores p dependen tanto de los (datos) observados como de otros (datos) posibles que podrían haberse observado pero no lo fueron"). ^[69]
• Confusión resultante (en parte) de la combinación de los métodos de Fisher y Neyman-Pearson, que son conceptualmente distintos. ^[60]
• Énfasis en la significación estadística con exclusión de la estimación y confirmación mediante experimentos repetidos. ^[70]
• Exigir de forma estricta la significación estadística como criterio de publicación, lo que da lugar a un sesgo de publicación . ^[71] La mayor parte de las críticas son indirectas. En lugar de estar equivocadas, las pruebas de hipótesis estadísticas se malinterpretan, se utilizan en exceso y se usan incorrectamente.
• Cuando se utiliza para detectar si existe una diferencia entre grupos, surge una paradoja. A medida que se realizan mejoras en el diseño experimental (por ejemplo, mayor precisión de la medición y tamaño de la muestra), la prueba se vuelve más indulgente. A menos que se acepte la suposición absurda de que todas las fuentes de ruido en los datos se cancelan completamente, la probabilidad de encontrar significación estadística en cualquier dirección se acerca al 100%. ^[72] Sin embargo, esta suposición absurda de que la diferencia media entre dos grupos no puede ser cero implica que los datos no pueden ser independientes e idénticamente distribuidos (iid) porque la diferencia esperada entre dos subgrupos cualesquiera de variables aleatorias iid es cero; por lo tanto, la suposición iid también es absurda.
• Capas de preocupaciones filosóficas. La probabilidad de significación estadística es una función de las decisiones tomadas por los experimentadores/analistas. ^[73] Si las decisiones se basan en la convención se las califica de arbitrarias o irreflexivas ^[74] mientras que las que no se basan en eso pueden calificarse de subjetivas. Para minimizar los errores de tipo II, se recomiendan muestras grandes. En psicología, prácticamente todas las hipótesis nulas se consideran falsas para muestras suficientemente grandes, por lo que "... suele ser absurdo realizar un experimento con el único objetivo de rechazar la hipótesis nula". ^[75] "Los hallazgos estadísticamente significativos suelen ser engañosos" en psicología. ^[76] La significación estadística no implica significación práctica, y la correlación no implica causalidad . Poner en duda la hipótesis nula está, por tanto, lejos de respaldar directamente la hipótesis de investigación.
• "No nos dice lo que queremos saber". ^[77] Hay listas de docenas de quejas disponibles. ^{[67] [78] [79]}

Los críticos y los partidarios coinciden en gran medida en cuanto a las características de las pruebas de significación de la hipótesis nula (NHST): si bien pueden proporcionar información crítica, son inadecuadas como única herramienta para el análisis estadístico . Rechazar con éxito la hipótesis nula puede no ofrecer ningún respaldo a la hipótesis de investigación. La controversia continua se refiere a la selección de las mejores prácticas estadísticas para el futuro cercano dadas las prácticas existentes. Sin embargo, un diseño de investigación adecuado puede minimizar este problema. Los críticos preferirían prohibir las NHST por completo, lo que obligaría a abandonar por completo esas prácticas, ^[80] mientras que los partidarios sugieren un cambio menos absoluto. ^{[ cita requerida ]}

La controversia sobre las pruebas de significación, y sus efectos sobre el sesgo de publicación en particular, ha producido varios resultados. La Asociación Estadounidense de Psicología ha reforzado sus requisitos de informes estadísticos después de la revisión, ^{[81] los editores} de revistas médicas han reconocido la obligación de publicar algunos resultados que no son estadísticamente significativos para combatir el sesgo de publicación, ^[82] y se ha creado una revista ( Journal of Articles in Support of the Null Hypothesis ) para publicar exclusivamente dichos resultados. ^[83] Los libros de texto han añadido algunas precauciones, ^[84] y han aumentado la cobertura de las herramientas necesarias para estimar el tamaño de la muestra requerida para producir resultados significativos. Pocas organizaciones importantes han abandonado el uso de pruebas de significación, aunque algunas han discutido hacerlo. ^[81] Por ejemplo, en 2023, los editores del Journal of Physiology "recomiendan encarecidamente el uso de métodos de estimación para quienes publican en el Journal" (es decir, la magnitud del tamaño del efecto (para permitir que los lectores juzguen si un hallazgo tiene relevancia práctica, fisiológica o clínica) e intervalos de confianza para transmitir la precisión de esa estimación), diciendo "En última instancia, es la importancia fisiológica de los datos lo que más debería preocupar a quienes publican en el Journal of Physiology, en lugar de la significación estadística". ^[85]

Alternativas

Una posición unificadora de los críticos es que las estadísticas no deberían llevar a una conclusión o decisión de aceptar o rechazar, sino a un valor estimado con una estimación de intervalo ; esta filosofía de análisis de datos se conoce en términos generales como estadísticas de estimación . Las estadísticas de estimación se pueden lograr con métodos frecuentistas [1] o bayesianos. ^{[86] [87]}

Los críticos de las pruebas de significación han defendido que la inferencia se base menos en los valores p y más en los intervalos de confianza para los tamaños del efecto en el caso de la importancia, los intervalos de predicción para la confianza, las réplicas y extensiones para la replicabilidad y los metaanálisis para la generalidad. ^[88] Pero ninguna de estas alternativas sugeridas produce inherentemente una decisión. Lehmann dijo que la teoría de las pruebas de hipótesis se puede presentar en términos de conclusiones/decisiones, probabilidades o intervalos de confianza: "La distinción entre los... enfoques es en gran medida una de presentación de informes e interpretación". ^[25]

La inferencia bayesiana es una alternativa propuesta a las pruebas de significancia. (Nickerson citó 10 fuentes que la sugieren, incluyendo Rozeboom (1960)). ^[78] Por ejemplo, la estimación de parámetros bayesianos puede proporcionar información rica sobre los datos de los cuales los investigadores pueden extraer inferencias, mientras que se utilizan valores previos inciertos que ejercen solo una influencia mínima en los resultados cuando hay suficientes datos disponibles. El psicólogo John K. Kruschke ha sugerido la estimación bayesiana como una alternativa para la prueba t ^[86] y también ha contrastado la estimación bayesiana para evaluar valores nulos con la comparación de modelos bayesianos para pruebas de hipótesis. ^[87] Dos modelos/hipótesis en competencia se pueden comparar utilizando factores de Bayes . ^[89] Los métodos bayesianos podrían ser criticados por requerir información que rara vez está disponible en los casos en que las pruebas de significancia se utilizan con mayor frecuencia. Ni las probabilidades previas ni la distribución de probabilidad de la estadística de prueba bajo la hipótesis alternativa suelen estar disponibles en las ciencias sociales. ^[78]

Los defensores de un enfoque bayesiano a veces afirman que el objetivo de un investigador es, en la mayoría de los casos, evaluar objetivamente la probabilidad de que una hipótesis sea verdadera basándose en los datos que ha recopilado. ^{[90] [91]} Ni la prueba de significancia de Fisher ni la prueba de hipótesis de Neyman-Pearson pueden proporcionar esta información, y no afirman hacerlo. La probabilidad de que una hipótesis sea verdadera solo se puede derivar del uso del teorema de Bayes , que no era satisfactorio para los bandos de Fisher y Neyman-Pearson debido al uso explícito de la subjetividad en forma de probabilidad previa . ^{[11] [92]} La estrategia de Fisher es eludir esto con el valor p (un índice objetivo basado solo en los datos) seguido de inferencia inductiva , mientras que Neyman-Pearson ideó su enfoque de comportamiento inductivo .

Véase también

• Portal de matemáticas

• Estadística
• Problema de Behrens-Fisher
• Bootstrapping (estadísticas)
• Cómo comprobar si una moneda es justa
• Árbol de decisión de prueba de comparación de medios
• Aleatoriedad espacial completa
• Contra-nulo
• Falsabilidad
• Método de Fisher para combinar pruebas independientes de significación
• Causalidad de Granger
• Efecto de mirar hacia otro lado
• Problema de unidad de área modificable
• Problema de unidad temporal modificable
• Prueba de hipótesis multivariante
• Prueba ómnibus
• Pensamiento dicotómico
• Prueba de hipótesis casi segura
• Criterio de información de Akaike
• Criterio de información bayesiano
• Valores E

Referencias

1. Lewis, Nancy D.; Lewis, Nigel Da Costa; Lewis, ND (2013). 100 pruebas estadísticas en R: qué elegir, cómo calcularlas fácilmente, con más de 300 ilustraciones y ejemplos. Heather Hills Press. ISBN 978-1-4840-5299-0.
2. Kanji, Gopal K. (18 de julio de 2006). 100 pruebas estadísticas. SAGE. ISBN 978-1-4462-2250-8.
3. Bellhouse, P. (2001), "John Arbuthnot", en Estadísticos de los siglos de CC Heyde y E. Seneta , Springer, págs. 39-42, ISBN 978-0-387-95329-8
4. Meehl, P (1990). "Evaluación y modificación de teorías: la estrategia de defensa lakatosiana y dos principios que la justifican" (PDF) . Psychological Inquiry . 1 (2): 108–141. doi :10.1207/s15327965pli0102_1.
5. Laplace, P. (1778). "Mémoire sur les probabilités" (PDF) . Mémoires de l'Académie Royale des Sciences de París . 9 : 227–332. Archivado desde el original (PDF) el 27 de abril de 2015 . Consultado el 5 de septiembre de 2013 .
6. Pearson, K (1900). "Sobre el criterio de que un sistema dado de desviaciones de lo probable en el caso de un sistema correlacionado de variables es tal que puede suponerse razonablemente que ha surgido de un muestreo aleatorio" (PDF) . The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 5 (50): 157–175. doi :10.1080/14786440009463897.
7. Pearson, K (1904). "Sobre la teoría de la contingencia y su relación con la asociación y la correlación normal". Memorias de investigación de la Drapers' Company, serie biométrica . 1 : 1–35.
8. Zabell, S (1989). "RA Fisher sobre la historia de la probabilidad inversa". Ciencia estadística . 4 (3): 247–256. doi : 10.1214/ss/1177012488 . JSTOR  2245634.
9. Raymond Hubbard, MJ Bayarri , Los valores P no son probabilidades de error Archivado el 4 de septiembre de 2013 en Wayback Machine . Documento de trabajo que explica la diferencia entre el valor p evidencial de Fisher y la tasa de error tipo I de Neyman-Pearson . ${\displaystyle \alpha }$
10. R (1955). "Métodos estadísticos e inducción científica" (PDF) . Revista de la Royal Statistical Society, Serie B. 17 (1): 69–78. doi :10.1111/j.2517-6161.1955.tb00180.x.
11. Neyman, J; Pearson, ES (1 de enero de 1933). "Sobre el problema de las pruebas más eficientes de hipótesis estadísticas". Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337. Bibcode :1933RSPTA.231..289N. doi : 10.1098/rsta.1933.0009 .
12. Goodman, SN (15 de junio de 1999). "Hacia estadísticas médicas basadas en evidencia. 1: La falacia del valor P". Ann Intern Med . 130 (12): 995–1004. doi :10.7326/0003-4819-130-12-199906150-00008. PMID  10383371. S2CID  7534212.
13. Lehmann, EL (diciembre de 1993). "Las teorías de Fisher, Neyman–Pearson sobre la prueba de hipótesis: ¿una teoría o dos?". Journal of the American Statistical Association . 88 (424): 1242–1249. doi :10.1080/01621459.1993.10476404.
14. Fisher, RN (1958). "La naturaleza de la probabilidad" (PDF) . Centennial Review . 2 : 261-274. Corremos el gran peligro de enviar al mundo a jóvenes muy preparados e inteligentes con tablas de números erróneos bajo el brazo y con una densa niebla en el lugar donde deberían estar sus cerebros. En este siglo, por supuesto, trabajarán en misiles teledirigidos y asesorarán a la profesión médica sobre el control de las enfermedades, y no hay límite en cuanto a la medida en que podrían obstaculizar todo tipo de esfuerzo nacional.
15. Lenhard, Johannes (2006). "Modelos e inferencia estadística: la controversia entre Fisher y Neyman-Pearson". Br. J. Philos. Sci . 57 : 69–91. doi :10.1093/bjps/axi152. S2CID  14136146.
16. Neyman, Jerzy (1967). "RA Fisher (1890—1962): una apreciación". Science . 156 (3781): 1456–1460. Bibcode :1967Sci...156.1456N. doi :10.1126/science.156.3781.1456. PMID  17741062. S2CID  44708120.
17. Losavich, JL; Neyman, J.; Scott, EL; Wells, MA (1971). "Explicaciones hipotéticas de los efectos negativos aparentes de la siembra de nubes en el experimento Whitetop". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 68 (11): 2643–2646. Bibcode :1971PNAS...68.2643L. doi : 10.1073/pnas.68.11.2643 . PMC 389491 . PMID  16591951. 
18. Halpin, PF; Stam, HJ (invierno de 2006). "Inferencia inductiva o comportamiento inductivo: Fisher y Neyman: enfoques de Pearson para las pruebas estadísticas en la investigación psicológica (1940-1960)". The American Journal of Psychology . 119 (4): 625–653. doi :10.2307/20445367. JSTOR  20445367. PMID  17286092.
19. Gigerenzer, Gerd; Zeno Swijtink; Theodore Porter; Lorraine Daston; John Beatty; Lorenz Kruger (1989). "Parte 3: Los expertos en inferencia". El imperio del azar: cómo la probabilidad cambió la ciencia y la vida cotidiana . Cambridge University Press. págs. 70–122. ISBN 978-0-521-39838-1.
20. Mayo, DG; Spanos, A. (2006). "Pruebas severas como concepto básico en una filosofía de inducción de Neyman-Pearson". The British Journal for the Philosophy of Science . 57 (2): 323–357. CiteSeerX 10.1.1.130.8131 . doi :10.1093/bjps/axl003. S2CID  7176653. 
21. Matemáticas > Secundaria: Estadística y probabilidad > Introducción Archivado el 28 de julio de 2012 en archive.today Iniciativa de estándares estatales básicos comunes (se relaciona con estudiantes de EE. UU.)
22. Pruebas del College Board > AP: Asignaturas > Estadística El College Board (se relaciona con los estudiantes de EE. UU.)
23. Huff, Darrell (1993). Cómo mentir con estadísticas. Nueva York: Norton. p. 8. ISBN 978-0-393-31072-6.'Los métodos estadísticos y los términos estadísticos son necesarios para informar sobre los datos masivos de las tendencias sociales y económicas, las condiciones de los negocios, las encuestas de "opinión", el censo. Pero sin escritores que utilicen las palabras con honestidad y lectores que sepan lo que significan, el resultado sólo puede ser un sinsentido semántico.'
24. Snedecor, George W.; Cochran, William G. (1967). Métodos estadísticos (6.ª ed.). Ames, Iowa: Iowa State University Press. pág. 3."...las ideas básicas de la estadística nos ayudan a pensar con claridad sobre el problema, nos proporcionan cierta orientación sobre las condiciones que deben cumplirse para que se puedan hacer inferencias sólidas y nos permiten detectar muchas inferencias que no tienen una buena base lógica".
25. EL Lehmann (1997). "Prueba de hipótesis estadísticas: La historia de un libro". Ciencia estadística . 12 (1): 48–52. doi : 10.1214/ss/1029963261 .
26. Sotos, Ana Elisa Castro; Vanhoof, Stijn; Noortgate, Wim Van den; Onghena, Patrick (2007). "Ideas erróneas de los estudiantes sobre la inferencia estadística: una revisión de la evidencia empírica de la investigación sobre la enseñanza de la estadística" (PDF) . Educational Research Review . 2 (2): 98–113. doi :10.1016/j.edurev.2007.04.001.
27. Moore, David S. (1997). "Nueva pedagogía y nuevos contenidos: el caso de la estadística" (PDF) . Revista estadística internacional . 65 (2): 123–165. doi :10.2307/1403333. JSTOR  1403333.
28. Hubbard, Raymond; Armstrong, J. Scott (2006). "Por qué no sabemos realmente qué significa la significación estadística: implicaciones para los educadores". Revista de educación en marketing . 28 (2): 114–120. doi :10.1177/0273475306288399. hdl : 2092/413 . S2CID  34729227.
29. Sotos, Ana Elisa Castro; Vanhoof, Stijn; Noortgate, Wim Van den; Onghena, Patrick (2009). "¿Cuán confiados están los estudiantes en sus conceptos erróneos sobre las pruebas de hipótesis?". Journal of Statistics Education . 17 (2). doi : 10.1080/10691898.2009.11889514 .
30. Gigerenzer, G. (2004). "El ritual nulo: lo que siempre quiso saber sobre las pruebas significativas pero tenía miedo de preguntar" (PDF) . Manual SAGE de metodología cuantitativa para las ciencias sociales . pp. 391–408. doi :10.4135/9781412986311. ISBN 9780761923596.
31. "Prueba de hipótesis estadísticas". Springer Texts in Statistics . 2005. doi :10.1007/0-387-27605-x. ISBN 978-0-387-98864-1. ISSN  1431-875X.
32. Hinkelmann, Klaus; Kempthorne, Oscar (2008). Diseño y análisis de experimentos . Vol. I y II (segunda edición). Wiley. ISBN 978-0-470-38551-7.
33. Montgomery, Douglas (2009). Diseño y análisis de experimentos . Hoboken, NJ: Wiley. ISBN 978-0-470-12866-4.
34. RA Fisher (1925). Métodos estadísticos para investigadores , Edimburgo: Oliver y Boyd, 1925, pág. 43.
35. Lehmann, EL; Romano, Joseph P. (2005). Prueba de hipótesis estadísticas (3.ª edición). Nueva York: Springer. ISBN 978-0-387-98864-1.
36. Nuzzo, Regina (2014). "Método científico: errores estadísticos". Nature . 506 (7487): 150–152. Bibcode :2014Natur.506..150N. doi : 10.1038/506150a . PMID  24522584.
37. Richard J. Larsen; Donna Fox Stroup (1976). Estadísticas en el mundo real: un libro de ejemplos . Macmillan. ISBN 978-0023677205.
38. Hubbard, R.; Parsa, AR; Luthy, MR (1997). "La difusión de las pruebas de significación estadística en psicología: el caso del Journal of Applied Psychology". Teoría y psicología . 7 (4): 545–554. doi :10.1177/0959354397074006. S2CID  145576828.
39. Moore, David (2003). Introducción a la práctica de la estadística . Nueva York: WH Freeman and Co., pág. 426. ISBN 9780716796572.
40. Ranganathan, Priya; Pramesh, C. S; Buyse, Marc (abril-junio de 2016). "Errores comunes en el análisis estadístico: los peligros de las pruebas múltiples". Perspect Clin Res . 7 (2): 106–107. doi : 10.4103/2229-3485.179436 . PMC 4840791 . PMID  27141478. 
41. Hughes, Ann J.; Grawoig, Dennis E. (1971). Estadística: una base para el análisis . Reading, Mass.: Addison-Wesley. pág. 191. ISBN 0-201-03021-7.
42. Hall, P. y Wilson, SR, 1991. Dos pautas para la prueba de hipótesis bootstrap. Biometrics, págs. 757-762.
43. Tibshirani, RJ y Efron, B., 1993. Una introducción al bootstrap. Monografías sobre estadística y probabilidad aplicada, 57(1).
44. Martin, MA, 2007. Pruebas de hipótesis bootstrap para algunos problemas estadísticos comunes: una evaluación crítica de las propiedades de tamaño y potencia. Computational Statistics & Data Analysis, 51(12), pp.6321-6342.
45. Horowitz, JL, 2019. Métodos bootstrap en econometría. Annual Review of Economics, 11, pp.193-224.
46. John Arbuthnot (1710). "Un argumento a favor de la Divina Providencia, tomado de la regularidad constante observada en los nacimientos de ambos sexos" (PDF) . Philosophical Transactions of the Royal Society of London . 27 (325–336): 186–190. doi : 10.1098/rstl.1710.0011 . S2CID  186209819.
47. Brian, Éric; Jaisson, Marie (2007). "Fisicoteología y matemáticas (1710-1794)". El origen de la proporción de sexos humanos al nacer . Springer Science & Business Media. págs. 1–25. ISBN 978-1-4020-6036-6.
48. Conover, WJ (1999), "Capítulo 3.4: La prueba de signos", Practical Nonparametric Statistics (tercera edición), Wiley, págs. 157-176, ISBN 978-0-471-16068-7
49. Sprent, P. (1989), Métodos estadísticos no paramétricos aplicados (segunda edición), Chapman & Hall, ISBN 978-0-412-44980-2
50. Stigler, Stephen M. (1986). Historia de la estadística: la medición de la incertidumbre antes de 1900. Harvard University Press. pp. 225–226. ISBN 978-0-67440341-3.
51. Laplace, P. (1778). "Mémoire sur les probabilités (XIX, XX)". Obras completas de Laplace . vol. 9. págs. 429–438. {{cite book}}: |journal=ignorado ( ayuda )
52. Stigler, Stephen M. (1986). Historia de la estadística: la medición de la incertidumbre antes de 1900. Cambridge, Mass.: Belknap Press de Harvard University Press. pág. 134. ISBN 978-0-674-40340-6.
53. Fisher, Sir Ronald A. (1956) [1935]. "Matemáticas de una dama que prueba el té". En James Roy Newman (ed.). El mundo de las matemáticas, volumen 3 [ Diseño de experimentos ]. Publicaciones Courier Dover. ISBN 978-0-486-41151-4.Originalmente del libro de Fisher Diseño de experimentos .
54. Box, Joan Fisher (1978). RA Fisher, La vida de un científico . Nueva York: Wiley. pág. 134. ISBN 978-0-471-09300-8.
55. CS Peirce (agosto de 1878). «Ilustraciones de la lógica de la ciencia VI: deducción, inducción e hipótesis». Popular Science Monthly . 13 . Consultado el 30 de marzo de 2012 .
56. Jaynes, ET (2007). Teoría de la probabilidad: la lógica de la ciencia (5.ª edición impresa). Cambridge [ua]: Cambridge Univ. Press. ISBN 978-0-521-59271-0.
57. Schervish, M (1996) Teoría de la estadística , p. 218. Saltador ISBN 0-387-94546-6 
58. Kaye, David H.; Freedman, David A. (2011). "Guía de referencia sobre estadística". Manual de referencia sobre evidencia científica (3.ª ed.). Eagan, MN; Washington, DC: West National Academies Press. pág. 259. ISBN 978-0-309-21421-6.
59. Ash, Robert (1970). Teoría básica de la probabilidad . Nueva York: Wiley. ISBN 978-0471034506.Sección 8.2
60. Tukey, John W. (1960). "Conclusiones vs decisiones". Technometrics . 26 (4): 423–433. doi :10.1080/00401706.1960.10489909."Hasta que no revisemos las explicaciones de las hipótesis de prueba, separando los elementos de decisión [de Neyman-Pearson] de los elementos de conclusión [de Fisher], la mezcla íntima de elementos dispares será una fuente continua de confusión". ... "Hay un lugar tanto para "hacer lo mejor que se pueda" como para "decir sólo lo que es cierto", pero es importante saber, en cada caso, tanto cuál se está haciendo como cuál se debería hacer".
61. Stigler, Stephen M. (agosto de 1996). "La historia de la estadística en 1933". Ciencia estadística . 11 (3): 244–252. doi : 10.1214/ss/1032280216 . JSTOR  2246117.
62. Berger, James O. (2003). "¿Podrían Fisher, Jeffreys y Neyman haber llegado a un acuerdo sobre las pruebas?". Statistical Science . 18 (1): 1–32. doi : 10.1214/ss/1056397485 .
63. Morrison, Denton; Henkel, Ramon, eds. (2006) [1970]. La controversia de la prueba de significación . Aldine Transaction. ISBN 978-0-202-30879-1.
64. Oakes, Michael (1986). Inferencia estadística: un comentario para las ciencias sociales y del comportamiento . Chichester, Nueva York: Wiley. ISBN 978-0471104438.
65. Chow, Siu L. (1997). Significación estadística: fundamento, validez y utilidad . Publicaciones SAGE. ISBN 978-0-7619-5205-3.
66. Harlow, Lisa Lavoie; Stanley A. Mulaik; James H. Steiger, eds. (1997). ¿Qué pasaría si no existieran pruebas de significación? . Lawrence Erlbaum Associates. ISBN 978-0-8058-2634-0.
67. Kline, Rex (2004). Más allá de las pruebas de significación: reforma de los métodos de análisis de datos en la investigación conductual . Washington, DC: Asociación Estadounidense de Psicología. ISBN 9781591471189.
68. McCloskey, Deirdre N.; Stephen T. Ziliak (2008). El culto a la significación estadística: cómo el error estándar nos cuesta empleos, justicia y vidas . University of Michigan Press. ISBN 978-0-472-05007-9.
69. Cornfield, Jerome (1976). "Contribuciones metodológicas recientes a los ensayos clínicos" (PDF) . American Journal of Epidemiology . 104 (4): 408–421. doi :10.1093/oxfordjournals.aje.a112313. PMID  788503.
70. Yates, Frank (1951). "La influencia de los métodos estadísticos para los investigadores en el desarrollo de la ciencia de la estadística". Revista de la Asociación Estadounidense de Estadística . 46 (253): 19–34. doi :10.1080/01621459.1951.10500764."El énfasis dado a las pruebas formales de significación a lo largo de los Métodos estadísticos [de R. A. Fisher] ... ha hecho que los investigadores científicos presten una atención indebida a los resultados de las pruebas de significación que realizan sobre sus datos, particularmente datos derivados de experimentos, y muy poca a las estimaciones de la magnitud de los efectos que están investigando". ... "El énfasis en las pruebas de significación y la consideración de los resultados de cada experimento de forma aislada han tenido la desafortunada consecuencia de que los investigadores científicos a menudo han considerado la ejecución de una prueba de significación sobre un experimento como el objetivo final".
71. Begg, Colin B.; Berlin, Jesse A. (1988). "Sesgo de publicación: un problema en la interpretación de datos médicos". Revista de la Royal Statistical Society, Serie A. 151 ( 3): 419–463. doi :10.2307/2982993. JSTOR  2982993. S2CID  121054702.
72. Meehl, Paul E. (1967). "Prueba de teorías en psicología y física: una paradoja metodológica" (PDF) . Filosofía de la ciencia . 34 (2): 103–115. doi :10.1086/288135. S2CID  96422880. Archivado desde el original (PDF) el 3 de diciembre de 2013.Treinta años después, Meehl reconoció que la teoría de la significación estadística era matemáticamente sólida, aunque siguió cuestionando la opción por defecto de la hipótesis nula, culpando en cambio a la "escasa comprensión de los científicos sociales de la relación lógica entre teoría y hecho" en "El problema es la epistemología, no la estadística: reemplazar las pruebas de significación por intervalos de confianza y cuantificar la exactitud de predicciones numéricas arriesgadas" (capítulo 14 en Harlow (1997)).
73. Bakan, David (1966). "La prueba de significación en la investigación psicológica". Psychological Bulletin . 66 (6): 423–437. doi :10.1037/h0020412. PMID  5974619.
74. Gigerenzer, G (noviembre de 2004). "Estadísticas sin sentido". The Journal of Socio-Economics . 33 (5): 587–606. doi :10.1016/j.socec.2004.09.033.
75. Nunnally, Jum (1960). "El lugar de la estadística en psicología". Medición educativa y psicológica . 20 (4): 641–650. doi :10.1177/001316446002000401. S2CID  144813784.
76. Lykken, David T. (1991). "¿Qué tiene de malo la psicología, de todos modos?". Pensar con claridad sobre psicología . 1 : 3–39.
77. Jacob Cohen (diciembre de 1994). "La Tierra es redonda (p < .05)". American Psychologist . 49 (12): 997–1003. doi :10.1037/0003-066X.49.12.997. S2CID  380942.Este artículo dio lugar a la revisión de las prácticas estadísticas por parte de la APA. Cohen fue miembro del grupo de trabajo que llevó a cabo la revisión.
78. Nickerson, Raymond S. (2000). "Pruebas de significación de hipótesis nula: una revisión de una controversia antigua y continua". Métodos psicológicos . 5 (2): 241–301. doi :10.1037/1082-989X.5.2.241. PMID  10937333. S2CID  28340967.
79. Branch, Mark (2014). "Efectos secundarios malignos de las pruebas de significación de la hipótesis nula". Teoría y psicología . 24 (2): 256–277. doi :10.1177/0959354314525282. S2CID  40712136.
80. Hunter, John E. (enero de 1997). "Necesidad: una prohibición de la prueba de significación". Psychological Science . 8 (1): 3–7. doi :10.1111/j.1467-9280.1997.tb00534.x. S2CID  145422959.
81. Wilkinson, Leland (1999). "Métodos estadísticos en revistas de psicología; directrices y explicaciones". American Psychologist . 54 (8): 594–604. doi :10.1037/0003-066X.54.8.594. S2CID  428023."Pruebas de hipótesis. Es difícil imaginar una situación en la que una decisión dicotómica de aceptar o rechazar sea mejor que informar un valor p real o, mejor aún, un intervalo de confianza" (p. 599). El comité utilizó el término de advertencia "tolerancia" para describir su decisión contra la prohibición de las pruebas de hipótesis en los informes de psicología (p. 603).
82. "ICMJE: Obligación de publicar estudios negativos". Archivado desde el original el 16 de julio de 2012. Consultado el 3 de septiembre de 2012. Los editores deben considerar seriamente la publicación de cualquier estudio realizado cuidadosamente sobre una cuestión importante, relevante para sus lectores, independientemente de si los resultados del resultado principal o de cualquier otro resultado adicional son estadísticamente significativos. La falta de presentación o publicación de los hallazgos debido a la falta de significación estadística es una causa importante de sesgo de publicación.
83. de la Revista de artículos en apoyo de la hipótesis nula : página de inicio de JASNH. El volumen 1, número 1, se publicó en 2002 y todos los artículos tratan sobre temas relacionados con la psicología.
84. Howell, David (2002). Métodos estadísticos para la psicología (5.ª ed.). Duxbury. pág. 94. ISBN 978-0-534-37770-0.
85. Williams S, Carson R, Tóth K (10 de octubre de 2023). "Más allá de los valores P en The Journal of Physiology: una introducción al valor de los tamaños del efecto y los intervalos de confianza". J Physiol . 601 (23): 5131–5133. doi : 10.1113/JP285575 . PMID  37815959. S2CID  263827430.{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
86. Kruschke, JK (9 de julio de 2012). "La estimación bayesiana reemplaza a la prueba T" (PDF) . Journal of Experimental Psychology: General . 142 (2): 573–603. doi :10.1037/a0029146. PMID  22774788. S2CID  5610231.
87. Kruschke, JK (8 de mayo de 2018). "Rechazar o aceptar valores de parámetros en la estimación bayesiana" (PDF) . Avances en métodos y prácticas en la ciencia psicológica . 1 (2): 270–280. doi :10.1177/2515245918771304. S2CID  125788648.
88. Armstrong, J. Scott (2007). "Las pruebas de significancia perjudican el progreso en la previsión". Revista Internacional de Previsión . 23 (2): 321–327. CiteSeerX 10.1.1.343.9516 . doi :10.1016/j.ijforecast.2007.03.004. S2CID  1550979. 
89. Kass, RE (1993). Factores bayesianos e incertidumbre del modelo (PDF) (Informe). Departamento de Estadística, Universidad de Washington.
90. Rozeboom, William W (1960). "La falacia de la prueba de significación de hipótesis nula" (PDF) . Psychological Bulletin . 57 (5): 416–428. CiteSeerX 10.1.1.398.9002 . doi :10.1037/h0042040. PMID  13744252. "...la aplicación adecuada de la estadística a la inferencia científica está irrevocablemente comprometida con la consideración extensiva de las probabilidades inversas [también conocidas como bayesianas]..." Se reconoció, con pesar, que las distribuciones de probabilidad a priori estaban disponibles "solo como una sensación subjetiva, que difería de una persona a otra" "en el futuro más inmediato, al menos".
91. Berger, James (2006). "El caso del análisis bayesiano objetivo". Análisis bayesiano . 1 (3): 385–402. doi : 10.1214/06-ba115 . Al enumerar las definiciones contrapuestas del análisis bayesiano "objetivo", el autor expresó que "un objetivo importante de la estadística (de hecho, de la ciencia) es encontrar una metodología bayesiana objetiva y completamente coherente para aprender de los datos".
92. Aldrich, J (2008). "RA Fisher sobre Bayes y el teorema de Bayes". Análisis bayesiano . 3 (1): 161–170. doi : 10.1214/08-BA306 .

Lectura adicional

• Lehmann EL (1992) "Introducción a Neyman y Pearson (1933) Sobre el problema de las pruebas más eficientes de hipótesis estadísticas". En: Breakthroughs in Statistics, Volumen 1 , (Eds Kotz, S., Johnson, NL), Springer-Verlag. ISBN 0-387-94037-5 (seguido de reimpresión del artículo) 
• Neyman, J.; Pearson, ES (1933). "Sobre el problema de las pruebas más eficientes de hipótesis estadísticas". Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337. Bibcode :1933RSPTA.231..289N. doi : 10.1098/rsta.1933.0009 .

Enlaces externos

• "Hipótesis estadísticas, verificación de", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Crítica bayesiana de las pruebas de hipótesis clásicas
• Crítica de las pruebas de hipótesis clásicas que pone de relieve las dudas de larga data de los estadísticos
• Descripción general de las pruebas estadísticas: cómo elegir la prueba estadística correcta
• [2] Método de prueba de hipótesis basado en análisis estadístico para el descubrimiento de conocimientos biológicos; Md. Naseef-Ur-Rahman Chowdhury, Suvankar Paul, Kazi Zakia Sultana

Calculadoras en línea

• Algunas calculadoras de valores p y pruebas de hipótesis.