Estructura estelar

Estructura de las estrellas

Sección transversal del Sol

Los modelos de estructura estelar describen la estructura interna de una estrella en detalle y hacen predicciones sobre la luminosidad , el color y la evolución futura de la estrella. Diferentes clases y edades de estrellas tienen diferentes estructuras internas, lo que refleja su composición elemental y sus mecanismos de transporte de energía.

Transporte de calor

Para el transporte de energía consulte Transferencia radiativa .

Los diferentes mecanismos de transporte de estrellas de masa alta, masa intermedia y masa baja

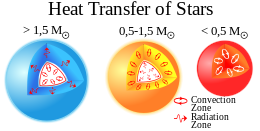
Las diferentes capas de las estrellas transportan calor hacia arriba y hacia afuera de diferentes maneras, principalmente por convección y transferencia radiativa , pero la conducción térmica es importante en las enanas blancas .

La convección es el modo dominante de transporte de energía cuando el gradiente de temperatura es lo suficientemente pronunciado como para que una determinada porción de gas dentro de la estrella continúe ascendiendo si asciende ligeramente mediante un proceso adiabático . En este caso, la porción ascendente es boyante y continúa ascendiendo si es más cálida que el gas circundante; si la porción ascendente es más fría que el gas circundante, volverá a caer a su altura original. ^[1] En regiones con un gradiente de temperatura bajo y una opacidad lo suficientemente baja como para permitir el transporte de energía mediante radiación, la radiación es el modo dominante de transporte de energía.

La estructura interna de una estrella de secuencia principal depende de la masa de la estrella.

En las estrellas con masas de 0,3 a 1,5 masas solares ( M ☉ ), incluido el Sol, la fusión de hidrógeno a helio se produce principalmente a través de cadenas protón-protón , que no establecen un gradiente de temperatura pronunciado. Por lo tanto, la radiación domina en la parte interior de las estrellas de masa solar. La parte exterior de las estrellas de masa solar es lo suficientemente fría como para que el hidrógeno sea neutro y, por lo tanto, opaco a los fotones ultravioleta, por lo que domina la convección. Por lo tanto, las estrellas de masa solar tienen núcleos radiativos con envolturas convectivas en la parte exterior de la estrella.

En las estrellas masivas (mayores de aproximadamente 1,5 M ☉ ), la temperatura del núcleo es superior a aproximadamente 1,8×10 ⁷ K , por lo que la fusión de hidrógeno a helio ocurre principalmente a través del ciclo CNO . En el ciclo CNO, la tasa de generación de energía escala como la temperatura a la 15.ª potencia, mientras que la tasa escala como la temperatura a la 4.ª potencia en las cadenas protón-protón. ^[2] Debido a la fuerte sensibilidad a la temperatura del ciclo CNO, el gradiente de temperatura en la parte interior de la estrella es lo suficientemente pronunciado como para hacer que el núcleo sea convectivo . En la parte exterior de la estrella, el gradiente de temperatura es más superficial, pero la temperatura es lo suficientemente alta como para que el hidrógeno esté casi completamente ionizado , por lo que la estrella permanece transparente a la radiación ultravioleta . Por lo tanto, las estrellas masivas tienen una envoltura radiativa .

Las estrellas de la secuencia principal de menor masa no tienen zona de radiación; el mecanismo de transporte de energía dominante en toda la estrella es la convección. ^[3]

Ecuaciones de la estructura estelar

El modelo más simple y comúnmente utilizado de la estructura estelar es el modelo cuasiestático de simetría esférica, que supone que una estrella está en un estado estable y que es esféricamente simétrica . Contiene cuatro ecuaciones diferenciales básicas de primer orden : dos representan cómo la materia y la presión varían con el radio; dos representan cómo la temperatura y la luminosidad varían con el radio. ^[4]

Al formar las ecuaciones de estructura estelar (explotando la simetría esférica supuesta), se considera la densidad de materia , temperatura , presión total (materia más radiación) , luminosidad y tasa de generación de energía por unidad de masa en una capa esférica de un espesor a una distancia del centro de la estrella. Se supone que la estrella está en equilibrio termodinámico local (LTE) por lo que la temperatura es idéntica para la materia y los fotones . Aunque LTE no se cumple estrictamente porque la temperatura que una capa dada "ve" debajo de sí misma es siempre más caliente que la temperatura por encima, esta aproximación normalmente es excelente porque el camino libre medio del fotón , , es mucho menor que la longitud sobre la cual la temperatura varía considerablemente, es decir . ${\displaystyle \rho (r)}$ ${\displaystyle T(r)}$ ${\displaystyle P(r)}$ ${\displaystyle l(r)}$ ${\displaystyle \epsilon (r)}$ ${\displaystyle {\mbox{d}}r}$ ${\displaystyle r}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda \ll T/|\nabla T|}$

En primer lugar, se hace referencia al equilibrio hidrostático : la fuerza hacia afuera debida al gradiente de presión dentro de la estrella se equilibra exactamente con la fuerza hacia adentro debida a la gravedad . A esto se lo denomina a veces equilibrio estelar.

${\displaystyle {{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho \over r^{2}}}$,

donde es la masa acumulada dentro de la capa en y G es la constante gravitacional . La masa acumulada aumenta con el radio según la ecuación de continuidad de masa : ${\displaystyle m(r)}$ ${\displaystyle r}$

${\displaystyle {{\mbox{d}}m \over {\mbox{d}}r}=4\pi r^{2}\rho .}$

Integrando la ecuación de continuidad de masa desde el centro de la estrella ( ) hasta el radio de la estrella ( ) se obtiene la masa total de la estrella. ${\displaystyle r=0}$ ${\displaystyle r=R}$

Considerando la energía que sale de la capa esférica se obtiene la ecuación de energía:

${\displaystyle {{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })}$,

donde es la luminosidad producida en forma de neutrinos (que suelen escapar de la estrella sin interactuar con la materia ordinaria) por unidad de masa. Fuera del núcleo de la estrella, donde se producen las reacciones nucleares, no se genera energía, por lo que la luminosidad es constante. ${\displaystyle \epsilon _{\nu }}$

La ecuación de transporte de energía adopta distintas formas según el modo de transporte de energía. Para el transporte de energía conductiva (apropiado para una enana blanca ), la ecuación de energía es

${\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{1 \over k}{l \over 4\pi r^{2}},}$

donde k es la conductividad térmica .

En el caso del transporte de energía radiativa, apropiado para la porción interna de una estrella de secuencia principal de masa solar y la envoltura externa de una estrella de secuencia principal masiva,

${\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 64\pi r^{2}\sigma T^{3}},}$

donde es la opacidad de la materia, es la constante de Stefan-Boltzmann , y la constante de Boltzmann se establece en uno. ${\displaystyle \kappa }$ ${\displaystyle \sigma }$

El caso del transporte de energía convectiva no tiene una formulación matemática rigurosa conocida e implica turbulencia en el gas. El transporte de energía convectiva generalmente se modela utilizando la teoría de longitud de mezcla . Esta trata el gas en la estrella como si contuviera elementos discretos que retienen aproximadamente la temperatura, la densidad y la presión de sus alrededores, pero se mueven a través de la estrella hasta una longitud característica, llamada longitud de mezcla . ^[5] Para un gas ideal monatómico , cuando la convección es adiabática , lo que significa que las burbujas de gas convectivo no intercambian calor con sus alrededores, la teoría de longitud de mezcla produce

${\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},}$

donde es el índice adiabático , la relación de calores específicos en el gas. (Para un gas ideal completamente ionizado , .) Cuando la convección no es adiabática, el gradiente de temperatura real no está dado por esta ecuación. Por ejemplo, en el Sol la convección en la base de la zona de convección, cerca del núcleo, es adiabática pero la que está cerca de la superficie no lo es. La teoría de la longitud de mezcla contiene dos parámetros libres que deben establecerse para que el modelo se ajuste a las observaciones, por lo que es una teoría fenomenológica en lugar de una formulación matemática rigurosa. ^[6] ${\displaystyle \gamma =c_{p}/c_{v}}$ ${\displaystyle \gamma =5/3}$

También se requieren las ecuaciones de estado , que relacionan la presión, la opacidad y la tasa de generación de energía con otras variables locales apropiadas para el material, como la temperatura, la densidad, la composición química, etc. Las ecuaciones de estado relevantes para la presión pueden tener que incluir la ley de los gases perfectos, la presión de radiación, la presión debida a los electrones degenerados, etc. La opacidad no se puede expresar exactamente con una única fórmula. Se calcula para varias composiciones a densidades y temperaturas específicas y se presenta en forma de tabla. ^[7] Los códigos de estructura estelar (es decir, los programas informáticos que calculan las variables del modelo) interpolan en una cuadrícula de densidad-temperatura para obtener la opacidad necesaria, o utilizan una función de ajuste basada en los valores tabulados. Una situación similar ocurre para los cálculos precisos de la ecuación de estado de presión. Finalmente, la tasa de generación de energía nuclear se calcula a partir de experimentos de física nuclear , utilizando redes de reacción para calcular las tasas de reacción para cada paso de reacción individual y las abundancias de equilibrio para cada isótopo en el gas. ^{[6] [8]}

Combinadas con un conjunto de condiciones de contorno , una solución de estas ecuaciones describe completamente el comportamiento de la estrella. Las condiciones de contorno típicas establecen los valores de los parámetros observables de manera apropiada en la superficie ( ) y el centro ( ) de la estrella: , lo que significa que la presión en la superficie de la estrella es cero; , no hay masa dentro del centro de la estrella, como se requiere si la densidad de masa permanece finita; , la masa total de la estrella es la masa de la estrella; y , la temperatura en la superficie es la temperatura efectiva de la estrella. ${\displaystyle r=R}$ ${\displaystyle r=0}$ ${\displaystyle P(R)=0}$ ${\displaystyle m(0)=0}$ ${\displaystyle m(R)=M}$ ${\displaystyle T(R)=T_{eff}}$

Aunque actualmente los modelos de evolución estelar describen las características principales de los diagramas de color-magnitud , se deben realizar mejoras importantes para eliminar las incertidumbres asociadas al conocimiento limitado de los fenómenos de transporte. El desafío más difícil sigue siendo el tratamiento numérico de la turbulencia. ^{[ cita requerida ]} Algunos equipos de investigación están desarrollando modelos simplificados de la turbulencia en cálculos 3D.

Evolución rápida

El modelo simplificado anterior no es adecuado sin modificaciones en situaciones en las que los cambios de composición son suficientemente rápidos. Puede ser necesario modificar la ecuación de equilibrio hidrostático añadiendo un término de aceleración radial si el radio de la estrella cambia muy rápidamente, por ejemplo, si la estrella pulsa radialmente. ^[9] Además, si la combustión nuclear no es estable o el núcleo de la estrella colapsa rápidamente, debe añadirse un término de entropía a la ecuación de energía. ^[10]

Véase también

• Portal de estrellas

• Altura de la escala
• Modelo solar estándar

Referencias

1. Hansen, Kawaler y Trimble (2004, §5.1.1)
2. Hansen, Kawaler y Trimble (2004, Tabla 1.1)
3. Hansen, Kawaler y Trimble (2004, §2.2.1)
4. Esta discusión sigue las de, por ejemplo, Zeilik y Gregory (1998, §16-1–16-2) y Hansen, Kawaler y Trimble (2004, §7.1)
5. Hansen, Kawaler y Trimble (2004, §5.1)
6. Ostlie, Dale A. y Carrol, Bradley W., Introducción a la astrofísica estelar moderna, Addison-Wesley (2007)
7. Iglesias, CA; Rogers, FJ (junio de 1996), "Opacidades de ópalo actualizadas", Astrophysical Journal , 464 : 943–+, Bibcode :1996ApJ...464..943I, doi :10.1086/177381.
8. Rauscher, T.; Heger, A.; Hoffman, RD; Woosley, SE (septiembre de 2002), "Nucleosíntesis en estrellas masivas con física nuclear y estelar mejorada", The Astrophysical Journal , 576 (1): 323–348, arXiv : astro-ph/0112478 , Bibcode :2002ApJ...576..323R, doi :10.1086/341728.
9. Moya, A.; Garrido, R. (agosto de 2008), "Código de oscilación de Granada (GraCo)", Astrophysics and Space Science , 316 (1–4): 129–133, arXiv : 0711.2590 , Bibcode :2008Ap&SS.316..129M, doi :10.1007/s10509-007-9694-2, S2CID  16150778.
10. Mueller, E. (julio de 1986), "Redes de reacción nuclear y códigos de evolución estelar: el acoplamiento de los cambios de composición y la liberación de energía en la combustión nuclear explosiva", Astronomía y Astrofísica , 162 (1–2): 103–108, Bibcode :1986A&A...162..103M.

Fuentes

• Kippenhahn, R.; Weigert, A. (1990), Estructura y evolución estelar , Springer-Verlag
• Hansen, Carl J.; Kawaler, Steven D.; Trimble, Virginia (2004), Stellar Interiors (2.ª ed.), Springer, ISBN 0-387-20089-4
• Kennedy, Dallas C.; Bludman, Sidney A. (1997), "Principios variacionales para la estructura estelar", Astrophysical Journal , 484 (1): 329–340, arXiv : astro-ph/9610099 , Bibcode :1997ApJ...484..329K, doi :10.1086/304333, S2CID  16835178
• Weiss, Achim; Hillebrandt, Wolfgang; Thomas, Hans-Christoph; Ritter, H. (2004), Principios de estructura estelar de Cox y Giuli , Cambridge Scientific Publishers, Bibcode :2004cgps.book.....W
• Zeilik, Michael A.; Gregory, Stephan A. (1998), Introducción a la astronomía y la astrofísica (4.ª ed.), Saunders College Publishing, ISBN 0-03-006228-4

Enlaces externos

• Código de opacidad recuperado en noviembre de 2009
• El código CESAM amarillo, evolución estelar y estructura Código fuente Fortran
• EZ to Evolve ZAMS Stars es un software FORTRAN 90 derivado del Stellar Evolution Code de Eggleton; aquí se puede encontrar una interfaz basada en web [1].
• Cuadrículas de Ginebra de modelos de evolución estelar (algunas de ellas incluyen mezcla inducida por rotación)
• La base de datos BaSTI de pistas de evolución estelar
• Atmósferas estelares: una contribución al estudio observacional de las altas temperaturas en las capas inversas de las estrellas, (1925) por Cecilia Payne-Gaposchkin, Cambridge: The Observatory.