juicio de Bernoulli

Cualquier experimento con dos posibles resultados aleatorios.

Gráficos de probabilidad P de no observar eventos independientes, cada uno de probabilidad p después de n ensayos de Bernoulli vs np para varios p . Se muestran tres ejemplos:
Curva azul : Lanzar un dado de 6 caras 6 veces da un 33,5% de posibilidades de que 6 (o cualquier otro número determinado) nunca aparezca; Se puede observar que a medida que n aumenta, la probabilidad de que un evento de probabilidad 1/ n nunca aparezca después de n intentos converge rápidamente a 0 .
Curva gris : para obtener una probabilidad de 50-50 de lanzar un Yahtzee (5 dados cúbicos que muestren todos el mismo número) se requieren 0,69 × 1296 ~ 898 lanzamientos.
Curva verde : Sacar una carta de una baraja de naipes sin comodines 100 (1,92 × 52) veces con reemplazo da un 85,7% de posibilidades de sacar el as de espadas al menos una vez.

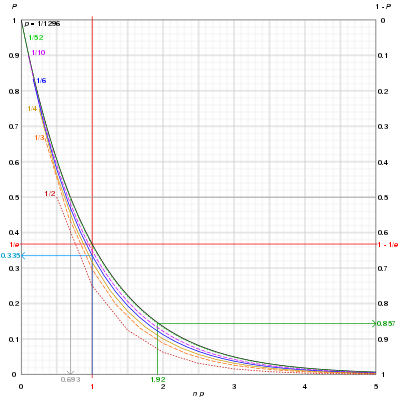
En la teoría de la probabilidad y la estadística , un ensayo de Bernoulli (o ensayo binomial ) es un experimento aleatorio con exactamente dos resultados posibles , "éxito" y "fracaso", en el que la probabilidad de éxito es la misma cada vez que se realiza el experimento. ^[1] Lleva el nombre de Jacob Bernoulli , un matemático suizo del siglo XVII, que los analizó en su Ars Conjectandi (1713). ^[2]

La formalización matemática del ensayo de Bernoulli se conoce como proceso de Bernoulli . Este artículo ofrece una introducción elemental al concepto, mientras que el artículo sobre el proceso de Bernoulli ofrece un tratamiento más avanzado.

Dado que un juicio de Bernoulli sólo tiene dos resultados posibles, puede formularse como una pregunta de "sí o no". Por ejemplo:

• ¿La primera carta de una baraja barajada es un as?
• ¿Era el recién nacido una niña? (Ver proporción de sexos humanos ).

Por lo tanto, el éxito y el fracaso son meras etiquetas para los dos resultados y no deben interpretarse literalmente. El término "éxito" en este sentido consiste en que el resultado cumpla condiciones específicas; No es un juicio de valor. De manera más general, dado cualquier espacio de probabilidad , para cualquier evento (conjunto de resultados), se puede definir un ensayo de Bernoulli, correspondiente a si el evento ocurrió o no (evento o evento complementario ). Ejemplos de ensayos de Bernoulli incluyen:

• Lanzar una moneda . En este contexto, el anverso ("cara") denota convencionalmente éxito y el reverso ("cruz") denota fracaso. Una moneda justa tiene una probabilidad de éxito de 0,5 por definición. En este caso, hay exactamente dos resultados posibles.
• Lanzar un dado , donde un seis es "éxito" y todo lo demás un "fracaso". En este caso, hay seis resultados posibles y el evento es seis; el evento complementario "no es un seis" corresponde a los otros cinco resultados posibles.
• Al realizar una encuesta de opinión política , se elige un votante al azar para determinar si ese votante votará "sí" en un próximo referéndum.

Definición

Los ensayos repetidos independientes de un experimento con exactamente dos resultados posibles se denominan ensayos de Bernoulli. Llame a uno de los resultados "éxito" y al otro "fracaso". Sea la probabilidad de éxito en un ensayo de Bernoulli y sea la probabilidad de fracaso. Entonces la probabilidad de éxito y la probabilidad de fracaso suman uno, ya que son eventos complementarios: "éxito" y "fracaso" son mutuamente excluyentes y exhaustivos . Así, se tienen las siguientes relaciones: ${\displaystyle p}$ ${\displaystyle q}$

${\displaystyle p=1-q,\quad \quad q=1-p,\quad \quad p+q=1.}$

Alternativamente, se pueden expresar en términos de probabilidades : dada la probabilidad de éxito y de fracaso, las probabilidades a favor son y las probabilidades en contra son . Estas también se pueden expresar como números, dividiendo, obteniendo las probabilidades a favor, y las probabilidades en contra, : ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle p:q}$ ${\displaystyle q:p.}$ ${\displaystyle o_{f}}$ ${\displaystyle o_{a}}$

${\displaystyle {\begin{aligned}o_{f}&=p/q=p/(1-p)=(1-q)/q\\o_{a}&=q/p=(1-p)/p=q/(1-q).\end{aligned}}}$

Estos son inversos multiplicativos , por lo que se multiplican a 1, con las siguientes relaciones:

${\displaystyle o_{f}=1/o_{a},\quad o_{a}=1/o_{f},\quad o_{f}\cdot o_{a}=1.}$

En el caso de que un ensayo de Bernoulli represente un evento a partir de un número finito de resultados igualmente probables , donde uno de los resultados es un éxito y otro un fracaso, las probabilidades a favor son y las probabilidades en contra son . Esto produce las siguientes fórmulas para probabilidad y probabilidades: ${\displaystyle S}$ ${\displaystyle F}$ ${\displaystyle S:F}$ ${\displaystyle F:S.}$

${\displaystyle {\begin{aligned}p&=S/(S+F)\\q&=F/(S+F)\\o_{f}&=S/F\\o_{a}&=F/S.\end{aligned}}}$

Aquí las probabilidades se calculan dividiendo el número de resultados, no las probabilidades, pero la proporción es la misma, ya que estos ratios sólo difieren al multiplicar ambos términos por el mismo factor constante.

Las variables aleatorias que describen los ensayos de Bernoulli a menudo se codifican utilizando la convención de que 1 = "éxito", 0 = "fracaso".

Estrechamente relacionado con un ensayo de Bernoulli está el experimento binomial, que consta de un número fijo de ensayos de Bernoulli estadísticamente independientes , cada uno con una probabilidad de éxito , y cuenta el número de éxitos. Una variable aleatoria correspondiente a un experimento binomial se denota por y se dice que tiene una distribución binomial . La probabilidad de éxito exacto en el experimento viene dada por: ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle B(n,p)}$ ${\displaystyle k}$ ${\displaystyle B(n,p)}$

${\displaystyle P(k)={n \choose k}p^{k}q^{n-k}}$

donde es un coeficiente binomial . ${\displaystyle {n \choose k}}$

Las pruebas de Bernoulli también pueden conducir a distribuciones binomiales negativas (que cuentan el número de éxitos en una serie de pruebas de Bernoulli repetidas hasta que se observa un número específico de fracasos), así como a otras distribuciones.

Cuando se realizan múltiples pruebas de Bernoulli, cada una con su propia probabilidad de éxito, a veces se las denomina pruebas de Poisson . ^[3]

Ejemplo: lanzar monedas

Considere el experimento sencillo en el que se lanza una moneda justa cuatro veces. Calcula la probabilidad de que exactamente dos de los lanzamientos resulten cara.

Solución

Una representación de los posibles resultados de lanzar una moneda justa cuatro veces en términos del número de caras. Como puede verse, la probabilidad de sacar exactamente dos caras en cuatro lanzamientos es 6/16 = 3/8, lo que coincide con los cálculos.

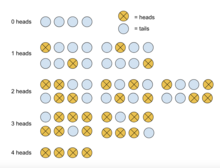
Para este experimento, definamos cara como un éxito y cruz como un fracaso. Como se supone que la moneda es justa, la probabilidad de éxito es . Por tanto, la probabilidad de fallo, , está dada por ${\displaystyle p={\tfrac {1}{2}}}$ ${\displaystyle q}$

${\displaystyle q=1-p=1-{\tfrac {1}{2}}={\tfrac {1}{2}}}$.

Usando la ecuación anterior, la probabilidad de que exactamente dos lanzamientos de un total de cuatro lanzamientos resulten en cara está dada por:

${\displaystyle {\begin{aligned}P(2)&={4 \choose 2}p^{2}q^{4-2}\\&=6\times \left({\tfrac {1}{2}}\right)^{2}\times \left({\tfrac {1}{2}}\right)^{2}\\&={\dfrac {3}{8}}.\end{aligned}}}$

Ver también

• Esquema de Bernoulli
• muestreo de Bernoulli
• Distribución de Bernoulli
• Distribución binomial
• Coeficiente binomial
• Intervalo de confianza de proporción binomial
• muestreo de veneno
• Diseño de muestreo
• Lanzamiento de moneda
• Jacob Bernoulli
• Prueba exacta de Fisher
• prueba de boschloo

Referencias

1. Papoulis, A. (1984). "Juicios de Bernoulli". Probabilidad, variables aleatorias y procesos estocásticos (2ª ed.). Nueva York: McGraw-Hill . págs. 57–63.
2. James Victor Uspensky: Introducción a la probabilidad matemática , McGraw-Hill, Nueva York 1937, página 45
3. Rajeev Motwani y P. Raghavan. Algoritmos aleatorios. Cambridge University Press, Nueva York (NY), 1995, páginas 67-68

enlaces externos

• "Ensayos de Bernoulli", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• "Simulación de n ensayos de Bernoulli". matemáticas.uah.edu . Consultado el 21 de enero de 2014 .