En geometría y en sus aplicaciones al dibujo , una perspectividad es la formación de una imagen en un plano pictórico de una escena vista desde un punto fijo.
La ciencia de la perspectiva gráfica utiliza perspectividades para crear imágenes realistas en proporciones adecuadas. Según Kirsti Andersen , el primer autor que describió la perspectividad fue Leon Alberti en su De Pictura (1435). [1] En inglés, Brook Taylor presentó su Perspectiva lineal en 1715, donde explicó que "la perspectiva es el arte de dibujar en un plano las apariencias de cualquier figura, mediante las reglas de la geometría". [2] En un segundo libro, Nuevos principios de la perspectiva lineal (1719), Taylor escribió
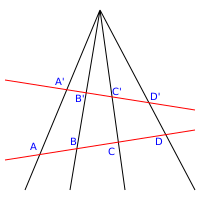
En geometría proyectiva los puntos de una recta se denominan rango proyectivo , y el conjunto de rectas en un plano sobre un punto se denomina lápiz .
Dadas dos líneas y en un plano proyectivo y un punto P de ese plano en ninguna línea, la aplicación biyectiva entre los puntos del rango de y el rango de determinado por las líneas del lápiz en P se llama perspectividad (o más precisamente, una perspectividad central con centro P ). [4] Se ha utilizado un símbolo especial para mostrar que los puntos X e Y están relacionados por una perspectividad; En esta notación, para mostrar que el centro de la perspectividad es P , escriba
La existencia de una perspectividad significa que los puntos correspondientes están en perspectiva . El concepto dual , perspectividad axial , es la correspondencia entre las líneas de dos lápices determinadas por un rango proyectivo.
La composición de dos perspectividades no es, en general, una perspectividad. Una perspectividad o una composición de dos o más perspectividades se denomina proyectividad ( transformación proyectiva , colineación proyectiva y homografía son sinónimos ).
Hay varios resultados relativos a proyectividades y perspectividades que se cumplen en cualquier plano proyectivo pappiano : [5]
Teorema: Cualquier proyectividad entre dos rangos proyectivos distintos puede escribirse como la composición de no más de dos perspectividades.
Teorema: Cualquier proyectividad desde un rango proyectivo hacia sí misma puede escribirse como la composición de tres perspectividades.
Teorema: Una proyectividad entre dos rangos proyectivos distintos que fija un punto es una perspectividad.
La correspondencia biyectiva entre puntos de dos líneas en un plano determinado por un punto de ese plano que no está en ninguna de las líneas tiene análogos de dimensiones superiores que también se llamarán perspectividades.
Sean S m y T m dos espacios proyectivos m -dimensionales distintos contenidos en un espacio proyectivo n -dimensional R n . Sea P n − m −1 un subespacio ( n − m − 1)-dimensional de R n sin puntos en común con S m o T m . Para cada punto X de S m , el espacio L generado por X y P n - m -1 se encuentra con T m en un punto Y = f P ( X ) . Esta correspondencia f P también se denomina perspectividad. [6] La perspectividad central descrita anteriormente es el caso con n = 2 y m = 1 .
Sean S 2 y T 2 dos planos proyectivos distintos en un 3-espacio proyectivo R 3 . Con O y O * siendo puntos de R 3 en ninguno de los planos, use la construcción de la última sección para proyectar S 2 sobre T 2 por la perspectividad con centro O seguida por la proyección de T 2 de vuelta sobre S 2 con la perspectividad con centro O *. Esta composición es una función biyectiva de los puntos de S 2 sobre sí misma que conserva los puntos colineales y se denomina colineación en perspectiva ( colineación central en la terminología más moderna). [7] Sea φ una colineación en perspectiva de S 2 . Cada punto de la línea de intersección de S 2 y T 2 estará fijado por φ y esta línea se denomina eje de φ. Sea el punto P la intersección de la línea OO * con el plano S 2 . P también está fijado por φ y cada línea de S 2 que pasa por P está estabilizada por φ (fija, pero no necesariamente fija puntualmente). P se denomina centro de φ. La restricción de φ a cualquier línea de S 2 que no pase por P es la perspectividad central en S 2 con centro P entre esa línea y la línea que es su imagen bajo φ.
