En el procesamiento de señales , en particular en el procesamiento de imágenes digitales , los artefactos de zumbido son artefactos que aparecen como señales espurias cerca de transiciones bruscas en una señal. Visualmente, aparecen como bandas o "fantasmas" cerca de los bordes; audiblemente, aparecen como "ecos" cerca de transitorios , en particular sonidos de instrumentos de percusión ; los más notables son los preecos . El término "zumbido" se debe a que la señal de salida oscila a una velocidad de desvanecimiento alrededor de una transición brusca en la entrada, similar a una campana después de ser golpeada. Al igual que con otros artefactos, su minimización es un criterio en el diseño de filtros .
La causa principal de los artefactos de zumbido se debe a que una señal está limitada en banda (específicamente, no tiene frecuencias altas) o pasa a través de un filtro de paso bajo ; esta es la descripción del dominio de la frecuencia . En términos del dominio del tiempo , la causa de este tipo de zumbido son las ondulaciones en la función sinc , [1] que es la respuesta al impulso (representación del dominio del tiempo) de un filtro de paso bajo perfecto. Matemáticamente, esto se llama el fenómeno de Gibbs .
Se puede distinguir entre sobreimpulso (y subimpulso), que ocurre cuando las transiciones se acentúan (la salida es más alta que la entrada), y el repliegue, donde después de un sobreimpulso, la señal se sobrecorrige y ahora está por debajo del valor objetivo; estos fenómenos a menudo ocurren juntos y, por lo tanto, a menudo se combinan y se denominan conjuntamente "repique".
El término "ringing" se utiliza con mayor frecuencia para las ondulaciones en el dominio del tiempo , aunque también se utiliza a veces para efectos del dominio de la frecuencia : [2] aplicar una ventana a un filtro en el dominio del tiempo mediante una función rectangular provoca ondulaciones en el dominio de la frecuencia por la misma razón que un filtro de paso bajo de pared de ladrillos (función rectangular en el dominio de la frecuencia ) provoca ondulaciones en el dominio del tiempo , siendo en cada caso la transformada de Fourier de la función rectangular la función sinc.
Existen artefactos relacionados causados por otros efectos del dominio de frecuencia y artefactos similares debido a causas no relacionadas.


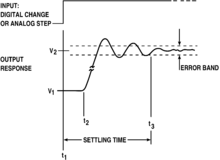
Por definición, el repique ocurre cuando una entrada no oscilante produce una salida oscilante: formalmente, cuando una señal de entrada que es monótona en un intervalo tiene una respuesta de salida que no es monótona. Esto ocurre con mayor gravedad cuando la respuesta al impulso o la respuesta al escalón de un filtro tiene oscilaciones; de manera menos formal, si para una entrada de pico o una entrada de escalón (una transición brusca), la salida tiene protuberancias. El repique se refiere más comúnmente al repique escalonado, y en ese nos centraremos.
El repique está estrechamente relacionado con el sobreimpulso y el subimpulso, que es cuando la salida toma valores superiores al valor de entrada máximo (respectivamente, inferiores al mínimo): se puede tener uno sin el otro, pero en casos importantes, como un filtro de paso bajo , primero se produce un sobreimpulso, luego la respuesta rebota por debajo del nivel de estado estable, lo que provoca el primer repique, y luego oscila de un lado a otro por encima y por debajo del nivel de estado estable. Por lo tanto, el sobreimpulso es el primer paso del fenómeno, mientras que el repique es el segundo paso y los subsiguientes. Debido a esta estrecha conexión, los términos a menudo se confunden, y "repique" se refiere tanto al sobreimpulso inicial como a los repiques posteriores.
Si se tiene un filtro lineal invariante en el tiempo (LTI), se puede entender el filtro y la oscilación en términos de la respuesta al impulso (la perspectiva del dominio del tiempo) o en términos de su transformada de Fourier, la respuesta de frecuencia (la perspectiva del dominio de la frecuencia). La oscilación es un artefacto del dominio del tiempo y, en el diseño de filtros , se compensa con las características deseadas del dominio de la frecuencia: la respuesta de frecuencia deseada puede causar oscilación, mientras que la reducción o eliminación de la oscilación puede empeorar la respuesta de frecuencia.

El ejemplo central, y a menudo lo que se entiende por "artefactos de timbre", es el filtro de paso bajo ideal ( de pared de ladrillos ) , el filtro sinc . Este tiene una función de respuesta al impulso oscilatoria, como se ilustra arriba, y la respuesta al escalón (su integral, la integral sinusoidal ) también presenta oscilaciones, como se ilustra a la derecha.
Estos artefactos de zumbido no son resultado de una implementación o ventana imperfecta: el filtro de paso bajo ideal, si bien posee la respuesta de frecuencia deseada, necesariamente causa artefactos de zumbido en el dominio del tiempo .
En términos de respuesta al impulso, la correspondencia entre estos artefactos y el comportamiento de la función es la siguiente:
En cuanto a la respuesta al escalón, la respuesta al escalón es la integral de la respuesta al impulso ; formalmente, el valor de la respuesta al escalón en el momento a es la integral de la respuesta al impulso. Por lo tanto, los valores de la respuesta al escalón se pueden entender en términos de integrales de cola de la respuesta al impulso.
Suponga que la integral general de la respuesta al impulso es 1, por lo que envía una entrada constante a la misma constante como salida; de lo contrario, el filtro tiene ganancia y el escalado por ganancia da una integral de 1.
La respuesta al impulso puede tener muchos lóbulos negativos y, por lo tanto, muchas oscilaciones, cada una de las cuales produce un anillo, aunque estos decaen en los filtros prácticos y, por lo tanto, generalmente solo se ven unos pocos anillos, siendo el primero generalmente el más pronunciado.
Tenga en cuenta que si la respuesta al impulso tiene lóbulos negativos pequeños y lóbulos positivos más grandes, entonces exhibirá oscilación pero no subimpulso ni sobreimpulso: la integral de cola siempre estará entre 0 y 1, pero oscilará hacia abajo en cada lóbulo negativo. Sin embargo, en el filtro sinc, los lóbulos disminuyen monótonamente en magnitud y se alternan en signo, como en la serie armónica alternada , y por lo tanto, las integrales de cola también se alternan en signo, por lo que exhibe sobreimpulso y oscilación.
Por el contrario, si la respuesta al impulso es siempre no negativa, por lo que no tiene lóbulos negativos (la función es una distribución de probabilidad ), entonces la respuesta al escalón no exhibirá oscilaciones ni sobreimpulsos ni subimpulsos, sino que será una función monótona que crece de 0 a 1, como una función de distribución acumulativa . Por lo tanto, la solución básica desde la perspectiva del dominio del tiempo es utilizar filtros con una respuesta al impulso no negativa.
La perspectiva del dominio de frecuencia es que el zumbido es causado por el corte brusco en la banda de paso rectangular en el dominio de frecuencia y, por lo tanto, se reduce mediante una caída más suave , como se analiza a continuación. [1] [4]
Las soluciones dependen de los parámetros del problema: si la causa es un filtro de paso bajo, se puede elegir un diseño de filtro diferente, que reduce los artefactos a expensas de un peor rendimiento en el dominio de frecuencia. Por otro lado, si la causa es una señal de banda limitada, como en JPEG, no se puede simplemente reemplazar un filtro, y los artefactos de zumbido pueden resultar difíciles de solucionar; están presentes en JPEG 2000 y en muchos códecs de compresión de audio (en forma de pre-eco ), como se analiza en los ejemplos.

Si la causa es el uso de un filtro de paso bajo de tipo pared de ladrillos, se puede reemplazar el filtro por uno que reduzca los artefactos en el dominio del tiempo, a costa del rendimiento en el dominio de la frecuencia. Esto se puede analizar desde la perspectiva del dominio del tiempo o del dominio de la frecuencia.
En el dominio del tiempo, la causa es una respuesta al impulso que oscila, asumiendo valores negativos. Esto se puede resolver utilizando un filtro cuya respuesta al impulso no sea negativa y no oscile, pero comparta las características deseadas. Por ejemplo, para un filtro de paso bajo, el filtro gaussiano no es negativo ni oscilatorio, por lo que no produce vibraciones. Sin embargo, no es tan bueno como un filtro de paso bajo: se desvanece en la banda de paso y se filtra en la banda de rechazo : en términos de imagen, un filtro gaussiano "desdibuja" la señal, lo que refleja la atenuación de las señales de frecuencia más alta deseadas en la banda de paso.
Una solución general es utilizar una función de ventana en el filtro sinc, que corta o reduce los lóbulos negativos: estos eliminan y reducen respectivamente el sobreimpulso y el zumbido. Nótese que truncar algunos pero no todos los lóbulos elimina el zumbido más allá de ese punto, pero no reduce la amplitud del zumbido que no está truncado (porque esto está determinado por el tamaño del lóbulo), y aumenta la magnitud del sobreimpulso si el último lóbulo no cortado es negativo, ya que la magnitud del sobreimpulso es la integral de la cola, que ya no es cancelada por los lóbulos positivos.
Además, en las implementaciones prácticas, al menos se trunca sinc, de lo contrario se deben usar infinitos puntos de datos (o más bien, todos los puntos de la señal) para calcular cada punto de la salida; el truncamiento corresponde a una ventana rectangular y hace que el filtro sea prácticamente implementable, pero la respuesta de frecuencia ya no es perfecta. [5] De hecho, si se toma un filtro de paso bajo de pared de ladrillos (sinc en el dominio del tiempo, rectangular en el dominio de la frecuencia) y se lo trunca (se lo multiplica con una función rectangular en el dominio del tiempo), esto convoluciona el dominio de la frecuencia con sinc (transformada de Fourier de la función rectangular) y provoca un zumbido en el dominio de la frecuencia , [2] que se conoce como rizado . En símbolos, el zumbido de frecuencia en la banda de supresión también se conoce como lóbulos laterales . La respuesta plana en la banda de paso es deseable, por lo que una ventana con funciones cuya transformada de Fourier tiene menos oscilaciones, por lo que el comportamiento en el dominio de la frecuencia es mejor.
La multiplicación en el dominio del tiempo corresponde a la convolución en el dominio de la frecuencia, por lo que multiplicar un filtro por una función de ventana corresponde a convolucionar la transformada de Fourier del filtro original por la transformada de Fourier de la ventana, lo que tiene un efecto de suavizado; por lo tanto, la creación de ventanas en el dominio del tiempo corresponde al suavizado en el dominio de la frecuencia y reduce o elimina el sobreimpulso y el zumbido. [6]
En el dominio de frecuencia , la causa puede interpretarse como debida al corte brusco (de pared de ladrillos) y al zumbido reducido mediante el uso de un filtro con una caída más suave. [1] Este es el caso del filtro gaussiano, cuyo diagrama de Bode de magnitud es una parábola de apertura hacia abajo (caída cuadrática), ya que su transformada de Fourier es nuevamente gaussiana, por lo tanto (hasta la escala) - tomando logaritmos se obtiene
En los filtros electrónicos , el equilibrio entre la respuesta en el dominio de la frecuencia y los artefactos de resonancia en el dominio del tiempo está bien ilustrado por el filtro Butterworth : la respuesta en frecuencia de un filtro Butterworth desciende linealmente en la escala logarítmica, con un filtro de primer orden que tiene una pendiente de −6 dB por octava , un filtro de segundo orden de –12 dB por octava y un filtro de orden n que tiene una pendiente de dB por octava; en el límite, esto se aproxima a un filtro de pared de ladrillos. Por lo tanto, entre estos, el filtro de primer orden es el que presenta la caída más lenta y, por lo tanto, exhibe la menor cantidad de artefactos en el dominio del tiempo, pero tiene más fugas en la banda de supresión, mientras que a medida que aumenta el orden, la fuga disminuye, pero los artefactos aumentan. [4]
Si bien los artefactos de zumbido generalmente se consideran indeseables, el sobreimpulso inicial (halo) en las transiciones aumenta la agudeza (nitidez aparente) al aumentar la derivada a lo largo de la transición y, por lo tanto, puede considerarse como una mejora. [8]

Otro artefacto es el sobreimpulso (y el subimpulso), que se manifiesta no como anillos, sino como un aumento del salto en la transición. Está relacionado con el repique y a menudo se produce en combinación con él.
El sobreimpulso y el subimpulso son causados por una cola negativa – en el sinc, la integral desde el primer cero hasta el infinito, incluyendo el primer lóbulo negativo. Mientras que el repique es causado por una cola positiva siguiente – en el sinc, la integral desde el segundo cero hasta el infinito, incluyendo el primer lóbulo positivo no central. Por lo tanto, el sobreimpulso es necesario para el repique, [ dudoso – discutir ] pero puede ocurrir por separado: por ejemplo, el filtro Lanczos de 2 lóbulos tiene solo un lóbulo negativo en cada lado, sin lóbulo positivo siguiente, y por lo tanto exhibe sobreimpulso pero no repique, mientras que el filtro Lanczos de 3 lóbulos exhibe tanto sobreimpulso como repique, aunque el enventanado reduce esto en comparación con el filtro sinc o el filtro sinc truncado.
De manera similar, el núcleo de convolución utilizado en la interpolación bicúbica es similar a un sinc con ventana de 2 lóbulos, que toma valores negativos y, por lo tanto, produce artefactos de sobreimpulso, que aparecen como halos en las transiciones.
A partir de los valores de sobreimpulso y subimpulso se produce el recorte . Si la señal está limitada, por ejemplo, un entero de 8 o 16 bits, este sobreimpulso o subimpulso puede superar el rango de valores permitidos, lo que provoca un recorte.
Estrictamente hablando, el recorte es causado por la combinación de sobreimpulso y precisión numérica limitada, pero está estrechamente asociado con el zumbido y a menudo ocurre en combinación con él.
El recorte también puede ocurrir por razones no relacionadas, como cuando una señal simplemente excede el rango de un canal.
Por otra parte, el recorte puede ser explotado para ocultar el efecto de zumbido en las imágenes. Algunos códecs JPEG modernos, como mozjpeg e ISO libjpeg , utilizan este truco para reducir el efecto de zumbido provocando deliberadamente sobreimpulsos en los resultados de IDCT. [9] Esta idea se originó en un parche de mozjpeg. [10]

En el procesamiento de señales y campos relacionados, el fenómeno general de la oscilación en el dominio del tiempo se denomina "ring" , mientras que las oscilaciones en el dominio de la frecuencia generalmente se denominan " ripple " , aunque generalmente no son "rippling".
Una fuente clave de ondulación en el procesamiento de señales digitales es el uso de funciones de ventana : si se toma un filtro de respuesta de impulso infinito (IIR), como el filtro sinc, y se le aplican ventanas para que tenga una respuesta de impulso finita , como en el método de diseño de ventanas , entonces la respuesta de frecuencia del filtro resultante es la convolución de la respuesta de frecuencia del filtro IIR con la respuesta de frecuencia de la función de ventana. En particular, la respuesta de frecuencia del filtro rectangular es la función sinc (la función rectangular y la función sinc son duales de Fourier entre sí), y por lo tanto el truncamiento de un filtro en el dominio del tiempo corresponde a la multiplicación por el filtro rectangular, por lo tanto la convolución por el filtro sinc en el dominio de la frecuencia, lo que causa ondulación. En símbolos, la respuesta de frecuencia de es En particular, truncar la función sinc en sí misma produce en el dominio del tiempo y en el dominio de la frecuencia, por lo que, así como el filtrado de paso bajo (truncamiento en el dominio de la frecuencia) causa vibración en el dominio del tiempo, el truncamiento en el dominio del tiempo (ventaneado mediante un filtro rectangular) causa ondulación en el dominio de la frecuencia.

La compresión JPEG puede generar artefactos de resonancia en transiciones nítidas, que son particularmente visibles en el texto.
Esto se debe a la pérdida de componentes de alta frecuencia, como en el caso de la respuesta escalonada. JPEG utiliza bloques de 8×8 , en los que se realiza la transformada discreta del coseno (DCT). La DCT es una transformada relacionada con Fourier y la respuesta escalonada se produce debido a la pérdida de componentes de alta frecuencia o a la pérdida de precisión en los componentes de alta frecuencia.
También pueden ocurrir en el borde de una imagen: dado que JPEG divide las imágenes en bloques de 8×8, si una imagen no es un número entero de bloques, el borde no se puede codificar fácilmente y soluciones como rellenar con un borde negro crean una transición nítida en la fuente, lo que genera artefactos resonantes en la imagen codificada.
El repiqueteo también ocurre en el JPEG 2000 basado en wavelets .
JPEG y JPEG 2000 tienen otros artefactos, como se ilustra arriba, como bloqueos (" dientes de sierra ") y bordes ocupados (" ruido de mosquito "), aunque estos se deben a características específicas de los formatos y no son sonidos como los que se analizan aquí.
Algunas ilustraciones:
En el procesamiento de señales de audio , el repique puede provocar que se produzcan ecos antes y después de los transitorios , como el sonido impulsivo de los instrumentos de percusión , como los platillos (esto es repique de impulso ). El eco ( causal ) después del transitorio no se escucha, porque está enmascarado por el transitorio, un efecto llamado enmascaramiento temporal . Por lo tanto, solo se escucha el eco ( anticausal ) antes del transitorio, y el fenómeno se llama preeco .
Este fenómeno ocurre como un artefacto de compresión en los algoritmos de compresión de audio que utilizan transformadas relacionadas con Fourier , como MP3 , AAC y Vorbis .
Otros fenómenos tienen síntomas similares a los del zumbido, pero por lo demás son distintos en cuanto a sus causas. En los casos en que estos causan artefactos circulares alrededor de fuentes puntuales, se los puede denominar "anillos" debido a su forma redonda (formalmente, un anillo ), que no está relacionada con el fenómeno de frecuencia del "zumbido" (decaimiento oscilatorio) que se analiza en esta página.
La mejora de bordes , cuyo objetivo es aumentar los bordes, puede provocar fenómenos de zumbido, en particular si se aplica repetidamente, como en el caso de un reproductor de DVD seguido de un televisor. Esto se puede lograr mediante un filtrado de paso alto , en lugar de un filtrado de paso bajo. [4]

Muchas funciones especiales presentan decaimiento oscilatorio y, por lo tanto, la convolución con dicha función produce vibraciones en la salida; se pueden considerar estas vibraciones o restringir el término a artefactos no deseados en el procesamiento de señales en el dominio de la frecuencia.
La difracción de Fraunhofer produce el disco de Airy como función de dispersión de puntos , que tiene un patrón de timbre.
La función de Bessel del primer tipo, que está relacionada con la función de Airy , exhibe dicha desintegración.
En las cámaras, una combinación de desenfoque y aberración esférica puede producir artefactos circulares (patrones de "anillos"). Sin embargo, el patrón de estos artefactos no tiene por qué ser similar al de los anillos (como se explica en esta página): pueden presentar una disminución oscilatoria (círculos de intensidad decreciente) u otros patrones de intensidad, como una única banda brillante.
El efecto fantasma es una forma de interferencia de televisión en la que se repite una imagen. Aunque no se trata de un zumbido, se puede interpretar como una convolución con una función que es 1 en el origen y ε (la intensidad del efecto fantasma) a cierta distancia, que es formalmente similar a las funciones anteriores (un único pico discreto, en lugar de una oscilación continua).
En fotografía, el destello de la lente es un defecto en el que pueden aparecer varios círculos alrededor de las partes resaltadas y con imágenes fantasma a lo largo de una fotografía, debido a la luz no deseada, como el reflejo y la dispersión de elementos en la lente.
Pueden producirse ilusiones visuales en las transiciones, como en las bandas de Mach , que muestran perceptualmente un subimpulso/sobreimpulso similar al fenómeno de Gibbs.