En la combinatoria poliédrica , una rama de las matemáticas, el teorema de Steinitz es una caracterización de los gráficos no dirigidos formados por las aristas y vértices de poliedros convexos tridimensionales : son exactamente los gráficos planos de 3 vértices conectados . Es decir, cada poliedro convexo forma un gráfico plano de 3 conexos, y cada gráfico plano de 3 conexos se puede representar como el gráfico de un poliedro convexo. Por esta razón, las gráficas planas de 3 conexos también se conocen como gráficas poliédricas . [1]
Este resultado proporciona un teorema de clasificación para los poliedros convexos tridimensionales, algo que no se conoce en dimensiones superiores. [2] Proporciona una descripción completa y puramente combinatoria de las gráficas de estos poliedros, permitiendo demostrar más fácilmente otros resultados sobre ellos, como el teorema de Eberhard sobre la realización de poliedros con determinados tipos de caras, sin referencia a la geometría. de estas formas. [3] Además, se ha aplicado en el dibujo de gráficos , como una forma de construir visualizaciones tridimensionales de gráficos abstractos. [4] Branko Grünbaum ha llamado a este teorema "el resultado más importante y más profundo conocido sobre 3 politopos ". [5]
El teorema aparece en una publicación de 1922 de Ernst Steinitz , [6] de quien lleva su nombre. Puede demostrarse mediante inducción matemática (como lo hizo Steinitz), encontrando el estado de energía mínima de un sistema de resorte bidimensional y elevando el resultado a tres dimensiones, o utilizando el teorema del empaquetamiento circular . Se conocen varias extensiones del teorema, en las que el poliedro que realiza un gráfico determinado tiene restricciones adicionales; por ejemplo, cada gráfico poliédrico es el gráfico de un poliedro convexo con coordenadas enteras, o el gráfico de un poliedro convexo, todos cuyos bordes son tangentes a una media esfera común .
Un gráfico no dirigido es un sistema de vértices y aristas , cada arista conecta dos de los vértices. Como es común en la teoría de grafos, a los efectos del teorema de Steinitz, estos gráficos están restringidos a ser finitos (los vértices y aristas son conjuntos finitos ) y simples (no hay dos aristas que conecten los mismos dos vértices, y ninguna arista conecta un vértice consigo misma) . A partir de cualquier poliedro se puede formar un gráfico, haciendo que los vértices del gráfico correspondan a los vértices del poliedro y conectando dos vértices cualesquiera del gráfico por una arista siempre que los dos vértices correspondientes del poliedro sean los puntos finales de una arista del poliedro. Este gráfico se conoce como el esqueleto del poliedro. [7]
Una gráfica es plana si se puede dibujar con sus vértices como puntos en el plano euclidiano y sus aristas como curvas que conectan estos puntos, de modo que no haya dos curvas de aristas que se crucen y que el punto que representa un vértice se encuentre en la curva. representar una arista solo cuando el vértice es un punto final de la arista. Según el teorema de Fáry , todo dibujo plano se puede enderezar de modo que las curvas que representan las aristas sean segmentos de recta . Un gráfico es conexo 3 si tiene más de tres vértices y, después de eliminar dos de sus vértices, cualquier otro par de vértices permanece conectado por un camino. El teorema de Steinitz establece que estas dos condiciones son necesarias y suficientes para caracterizar los esqueletos de poliedros convexos tridimensionales: una gráfica dada es la gráfica de un poliedro tridimensional convexo, si y solo si es plano y está conectado por 3 vértices. [5] [8]

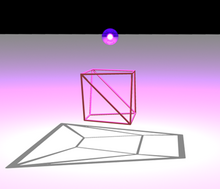
Una dirección del teorema de Steinitz (la dirección más fácil de demostrar) establece que la gráfica de todo poliedro convexo es plana y triconexa. Como se muestra en la ilustración, la planaridad se puede mostrar usando un diagrama de Schlegel : si uno coloca una fuente de luz cerca de una cara del poliedro y un plano en el otro lado, las sombras de los bordes del poliedro formarán un gráfico plano, incrustado. de tal forma que las aristas sean segmentos de recta. La conectividad tridimensional de un gráfico poliédrico es un caso especial del teorema de Balinski de que la gráfica de cualquier politopo convexo de dimensión es conexa. La conectividad del gráfico de un politopo, después de eliminar cualquiera de sus vértices, se puede probar eligiendo un vértice más , encontrando una función lineal que sea cero en el conjunto de vértices resultante y siguiendo los caminos generados por el método simplex para conectar. cada vértice a uno de los dos vértices extremos de la función lineal, con el vértice elegido conectado a ambos. [9]
La otra dirección, más difícil, del teorema de Steinitz establece que cada gráfico plano de 3 conexos es el gráfico de un poliedro convexo. Hay tres enfoques estándar para esta parte: pruebas por inducción, elevación de incrustaciones de Tutte bidimensionales a tres dimensiones utilizando la correspondencia de Maxwell-Cremona y métodos que utilizan el teorema de empaquetamiento de círculos para generar un poliedro canónico .

Aunque la prueba original de Steinitz no se expresó en términos de teoría de grafos, se puede reescribir en esos términos e implica encontrar una secuencia de transformaciones ΔY e YΔ que reduzcan cualquier gráfico plano de 3 conectados a , el gráfico del tetraedro. Una transformación YΔ elimina un vértice de grado tres de un gráfico, agregando aristas entre todos sus vecinos anteriores si esas aristas aún no existían; la transformación inversa, una transformación ΔY, elimina los bordes de un triángulo de un gráfico y los reemplaza por un nuevo vértice de grado tres adyacente a los mismos tres vértices. Una vez que se encuentra dicha secuencia, se puede invertir y convertir en operaciones geométricas que construyen el poliedro deseado paso a paso a partir de un tetraedro. Cada transformación YΔ en la secuencia invertida se puede realizar geométricamente cortando un vértice de grado tres de un poliedro. Se puede realizar geométricamente una transformación ΔY en la secuencia invertida quitando una cara triangular de un poliedro y extendiendo sus caras vecinas hasta el punto donde se encuentran, pero sólo cuando ese triple punto de intersección de las tres caras vecinas está en el lado más alejado de la cara eliminada del poliedro. Cuando el punto de triple intersección no está en el lado opuesto de esta cara, basta una transformación proyectiva del poliedro para moverlo hacia el lado correcto. Por lo tanto, por inducción sobre el número de transformaciones ΔY e YΔ necesarias para reducir un gráfico dado a , cada gráfico poliédrico se puede realizar como un poliedro. [5]
Un trabajo posterior de Epifanov reforzó la prueba de Steinitz de que todo gráfico poliédrico puede reducirse mediante transformaciones ΔY e YΔ. Epifanov demostró que si se especifican dos vértices en un gráfico plano, entonces el gráfico se puede reducir a un solo borde entre esos terminales combinando transformaciones ΔY e YΔ con reducciones en serie-paralelo . [10] La prueba de Epifanov era complicada y no constructiva, pero Truemper la simplificó utilizando métodos basados en gráficos menores . Truemper observó que cada gráfico de cuadrícula es reducible mediante transformaciones ΔY e YΔ de esta manera, que esta reducibilidad se conserva mediante gráficos menores y que cada gráfico plano es menor de un gráfico de cuadrícula. [11] Esta idea se puede utilizar para reemplazar el lema de Steinitz de que existe una secuencia de reducción. Después de esta sustitución, el resto de la prueba se puede realizar mediante inducción de la misma forma que la prueba original de Steinitz. [8] Para estas pruebas, realizadas utilizando cualquiera de las formas de encontrar secuencias de transformaciones ΔY- e YΔ-, existen gráficos poliédricos que requieren un número no lineal de pasos. Más precisamente, cada gráfico plano se puede reducir usando un número de pasos como máximo proporcional a , e infinitos gráficos requieren un número de pasos al menos proporcional a , donde es el número de vértices del gráfico. [12] [13]
Una forma alternativa de prueba de inducción se basa en eliminar los bordes (y comprimir los vértices de grado dos que podrían quedar después de esta eliminación) o contraer los bordes y formar una parte menor del gráfico plano dado. Cualquier gráfico poliédrico se puede reducir a un número lineal de estas operaciones, y nuevamente las operaciones se pueden invertir y las operaciones invertidas se pueden realizar geométricamente, dando una realización poliédrica del gráfico. Sin embargo, si bien es más sencillo demostrar que existe una secuencia de reducción para este tipo de argumento, y las secuencias de reducción son más cortas, los pasos geométricos necesarios para invertir la secuencia son más complicados. [14]
Si se dibuja una gráfica en el plano con aristas rectas, entonces una tensión de equilibrio se define como una asignación de números reales distintos de cero (pesos) a las aristas, con la propiedad de que cada vértice está en la posición dada por el promedio ponderado de sus aristas. vecinos. Según la correspondencia de Maxwell-Cremona, una tensión de equilibrio se puede elevar a una superficie tridimensional continua lineal por partes de modo que los bordes que forman los límites entre las partes planas de la superficie se proyecten al dibujo dado. El peso y la longitud de cada borde determinan la diferencia en las pendientes de la superficie a cada lado del borde, y la condición de que cada vértice esté en equilibrio con sus vecinos es equivalente a la condición de que estas diferencias de pendiente hagan que la superficie se encuentre con sí mismo correctamente en la vecindad del vértice. Los pesos positivos se traducen en ángulos diédricos convexos entre dos caras de la superficie lineal por partes, y los pesos negativos se traducen en ángulos diédricos cóncavos. Por el contrario, toda superficie lineal continua por tramos surge de esta manera de una tensión de equilibrio. Si se dibuja un gráfico plano finito y se le aplica una tensión de equilibrio de tal manera que todos los bordes interiores del dibujo tengan pesos positivos y todos los bordes exteriores tengan pesos negativos, entonces, al traducir esta tensión a una superficie tridimensional de esta manera, y luego reemplazando la superficie plana que representa el exterior del gráfico por su complemento en el mismo plano, se obtiene un poliedro convexo, con la propiedad adicional de que su proyección perpendicular sobre el plano no tiene cruces. [15] [16]
La correspondencia Maxwell-Cremona se ha utilizado para obtener realizaciones poliédricas de gráficos poliédricos combinándola con un método de dibujo de gráficos planos de WT Tutte , la incrustación de Tutte . El método de Tutte comienza fijando una cara de un gráfico poliédrico en una posición convexa en el plano. Esta cara se convertirá en la cara exterior del dibujo de un gráfico. El método continúa estableciendo un sistema de ecuaciones lineales en las coordenadas de los vértices, según el cual cada vértice restante debe ubicarse en el promedio de sus vecinos. Entonces, como demostró Tutte, este sistema de ecuaciones tendrá una solución única en la que cada cara del gráfico se dibuja como un polígono convexo. [17] Intuitivamente, esta solución describe el patrón que se obtendría reemplazando los bordes interiores del gráfico por resortes ideales y dejándolos asentarse en su estado de mínima energía. [18] El resultado es casi una tensión de equilibrio: si se asigna un peso uno a cada borde interior, entonces cada vértice interior del dibujo está en equilibrio. Sin embargo, no siempre es posible asignar números negativos a los bordes exteriores para que ellos también estén en equilibrio. Esta asignación siempre es posible cuando la cara exterior es un triángulo, por lo que este método se puede utilizar para realizar cualquier gráfico poliédrico que tenga una cara triangular. Si un gráfico poliédrico no contiene una cara triangular, su gráfico dual sí contiene un triángulo y también es poliédrico, por lo que se puede realizar el dual de esta manera y luego realizar el gráfico original como el poliedro polar de la realización dual. [4] [19] Un método alternativo para realizar poliedros utilizando elevaciones evita la dualidad eligiendo cualquier cara con un máximo de cinco vértices como cara exterior. Todo gráfico poliédrico tiene esa cara y, al elegir con más cuidado la forma fija de esta cara, se puede eliminar la incrustación de Tutte del resto del gráfico. [20]

Según una variante del teorema del empaquetamiento de círculos , para cada gráfico poliédrico, existe un sistema de círculos en el plano o en cualquier esfera, que representan los vértices y caras del gráfico, de modo que:
El mismo sistema de círculos forma una representación del gráfico dual intercambiando las funciones de los círculos que representan vértices y los círculos que representan caras. A partir de cualquier representación de este tipo en una esfera, incrustada en un espacio euclidiano tridimensional, se puede formar un poliedro convexo que es combinatoriamente equivalente al gráfico dado, como una intersección de semiespacios cuyos límites pasan por los círculos de las caras. De cada vértice de este poliedro, el horizonte de la esfera, visto desde ese vértice, es el círculo que la representa. Esta propiedad del horizonte determina la posición tridimensional de cada vértice, y el poliedro puede definirse de manera equivalente como la cáscara convexa de los vértices, posicionados de esta manera. La esfera se convierte en la esfera media de la realización: cada arista del poliedro es tangente a la esfera, en un punto donde dos círculos de vértice tangentes cruzan dos círculos de cara tangentes. [22]
Es posible demostrar una forma más sólida del teorema de Steinitz, que cualquier gráfico poliédrico puede realizarse mediante un poliedro convexo cuyas coordenadas sean números enteros . [23] Por ejemplo, la prueba original basada en la inducción de Steinitz puede reforzarse de esta manera. Sin embargo, los números enteros que resultarían de la construcción de Steinitz son doblemente exponenciales en el número de vértices del gráfico poliédrico dado. Escribir números de esta magnitud en notación binaria requeriría una cantidad exponencial de bits. [19] Geométricamente, esto significa que algunas características del poliedro pueden tener un tamaño doblemente exponencial más grande que otras, lo que hace que las realizaciones derivadas de este método sean problemáticas para aplicaciones en el dibujo de gráficos . [4]
Investigadores posteriores han encontrado algoritmos de realización basados en elevación que utilizan sólo un número lineal de bits por vértice. [20] [24] También es posible relajar el requisito de que las coordenadas sean números enteros y asignar coordenadas de tal manera que las coordenadas de los vértices sean números enteros distintos en el rango de 0 a y las otras dos coordenadas sean reales. números en el intervalo unitario , de modo que cada arista tenga una longitud de al menos uno, mientras que el poliedro general tenga un volumen lineal. [25] [26] Se sabe que algunos gráficos poliédricos se pueden realizar en cuadrículas de tamaño polinomial únicamente; en particular, esto es cierto para las pirámides (realizaciones de gráficos de ruedas ), prismas (realizaciones de gráficos de prismas ) y poliedros apilados (realizaciones de redes apolíneas ). [27]
Otra forma de afirmar la existencia de realizaciones enteras es que todo poliedro convexo tridimensional tiene un poliedro entero combinatoriamente equivalente. [23] Por ejemplo, el dodecaedro regular no es en sí mismo un poliedro entero, debido a sus caras regulares del pentágono, pero puede realizarse como un piritoedro entero equivalente . [20] Esto no siempre es posible en dimensiones superiores, donde existen politopos (como los construidos a partir de la configuración de Perles ) que no tienen un equivalente entero. [28]
Un gráfico de Halin es un caso especial de un gráfico poliédrico, formado a partir de un árbol plano incrustado (sin vértices de grado dos) conectando las hojas del árbol en un ciclo . Para los gráficos de Halin, se pueden elegir realizaciones poliédricas de un tipo especial: el ciclo exterior forma una cara base convexa horizontal, y cada dos caras se encuentra directamente encima de la cara base (como en los poliedros realizados mediante elevación), con todas estas caras superiores teniendo la misma pendiente. Se pueden construir superficies poliédricas con caras de igual pendiente sobre cualquier polígono base (no necesariamente convexo) a partir del esqueleto recto del polígono , y una forma equivalente de describir esta realización es que la proyección bidimensional del árbol sobre la cara base forma su recta. esqueleto. La prueba de este resultado utiliza la inducción: cualquier árbol enraizado puede reducirse a un árbol más pequeño eliminando las hojas de un nodo interno cuyos hijos son todos hojas, el gráfico de Halin formado a partir del árbol más pequeño se realiza mediante la hipótesis de inducción, y es Es posible modificar esta realización para agregar cualquier número de hijos de hoja al nodo del árbol cuyos hijos fueron eliminados. [29]
En cualquier poliedro que represente un gráfico poliédrico dado , las caras de son exactamente los ciclos que no se separan en dos componentes: es decir, eliminar un ciclo facial deja el resto como un subgrafo conectado. Estos ciclos se denominan ciclos periféricos . Por tanto, la estructura combinatoria de las caras (pero no sus formas geométricas) se determina únicamente a partir de la estructura del gráfico. Otro fortalecimiento del teorema de Steinitz, realizado por Barnette y Grünbaum, establece que para cualquier gráfico poliédrico, cualquier cara del gráfico y cualquier polígono convexo que represente esa cara, es posible encontrar una realización poliédrica de todo el gráfico que tenga la forma especificada para la cara designada. Esto está relacionado con el teorema de Tutte, según el cual cualquier gráfico poliédrico se puede dibujar en el plano con todas las caras convexas y cualquier forma especificada para su cara exterior. Sin embargo, los dibujos de gráficos planos producidos por el método de Tutte no necesariamente se elevan a poliedros convexos. En cambio, Barnette y Grünbaum prueban este resultado mediante un método inductivo. [30] También siempre es posible, dado un gráfico poliédrico y un ciclo arbitrario en , encontrar una realización para la cual se forma la silueta de la realización bajo proyección paralela . [31]
La realización de poliedros utilizando el teorema del empaquetamiento circular proporciona otro fortalecimiento del teorema de Steinitz: cada gráfico plano de 3 conexos puede representarse como un poliedro convexo de tal manera que todas sus aristas sean tangentes a la misma esfera unitaria , la esfera media de la poliedro. [22] Al realizar una transformación de Möbius cuidadosamente elegida de un empaquetamiento circular antes de transformarlo en un poliedro, es posible encontrar una realización poliédrica que realice todas las simetrías del gráfico subyacente, en el sentido de que cada automorfismo del gráfico es una simetría de la realización poliédrica. [32] [33] De manera más general, si es un gráfico poliédrico y es cualquier cuerpo convexo tridimensional liso , es posible encontrar una representación poliédrica en la que todas las aristas sean tangentes a . [34]
Los métodos de empaquetado de círculos también se pueden utilizar para caracterizar las gráficas de poliedros que tienen una circunesfera a través de todos sus vértices, o una inesfera tangente a todas sus caras. (Los poliedros con circunsfera también son significativos en geometría hiperbólica como poliedros ideales ). En ambos casos, la existencia de una esfera es equivalente a la solubilidad de un sistema de desigualdades lineales sobre variables reales positivas asociadas con cada borde del gráfico. En el caso de la esfera interior, estas variables deben sumar exactamente uno en cada ciclo facial del gráfico y más de uno en cada ciclo no facial. De manera dual, para la circunsfera, las variables deben sumar una en cada vértice y más de una en cada corte con dos o más vértices a cada lado del corte. Aunque puede haber exponencialmente muchas desigualdades lineales que satisfacer, se puede encontrar una solución (si existe) en tiempo polinómico utilizando el método del elipsoide . Los valores de las variables de una solución determinan los ángulos entre pares de círculos en un paquete circular cuyo poliedro correspondiente tiene la relación deseada con su esfera. [35] [36]

En cualquier dimensión superior a tres, el problema algorítmico de Steinitz consiste en determinar si una determinada red es la red de caras de un politopo convexo . Es poco probable que tenga complejidad de tiempo polinomial, ya que es NP-duro y más completo para la teoría existencial de los reales , incluso para politopos de cuatro dimensiones, según el teorema de universalidad de Richter-Gebert. [38] Aquí, la teoría existencial de los reales es una clase de problemas computacionales que pueden formularse en términos de encontrar variables reales que satisfagan un sistema dado de ecuaciones polinómicas y desigualdades. Para el problema algorítmico de Steinitz, las variables de dicho problema pueden ser las coordenadas del vértice de un politopo, y las ecuaciones y desigualdades se pueden usar para especificar la planitud de cada cara en la red de caras dada y la convexidad de cada ángulo entre caras. La completitud significa que todos los demás problemas de esta clase se pueden transformar en una instancia equivalente del problema algorítmico de Steinitz, en tiempo polinómico. La existencia de tal transformación implica que, si el problema algorítmico de Steinitz tiene una solución en tiempo polinómico, también la tiene todo problema de la teoría existencial de los reales y todo problema de NP. [39] Sin embargo, debido a que un gráfico dado puede corresponder a más de una red de caras, es difícil extender este resultado de completitud al problema de reconocer los gráficos de 4 politopos. La determinación de la complejidad computacional de este problema de reconocimiento de gráficos permanece abierta. [40]
Los investigadores también han encontrado caracterizaciones teóricas de grafos de las gráficas de ciertas clases especiales de poliedros tridimensionales no convexos [37] [41] y politopos convexos de cuatro dimensiones. [40] [42] [43] Sin embargo, en ambos casos, el problema general sigue sin resolverse. De hecho, incluso el problema de determinar qué gráficas completas son las gráficas de poliedros no convexos (aparte del tetraedro y del poliedro de Császár ) sigue sin resolverse. [44]
El teorema de Eberhard caracteriza parcialmente los múltiples conjuntos de polígonos que pueden combinarse para formar las caras de un poliedro convexo. Se puede demostrar formando un gráfico plano de 3 conexos con el conjunto dado de caras de polígono y luego aplicando el teorema de Steinitz para encontrar una realización poliédrica de ese gráfico. [3]
László Lovász ha mostrado una correspondencia entre representaciones poliédricas de gráficos y matrices que realizan las invariantes del gráfico de Colin de Verdière de los mismos gráficos. El invariante de Colin de Verdière es el corank máximo de una matriz de adyacencia ponderada del gráfico, bajo algunas condiciones adicionales que son irrelevantes para los gráficos poliédricos. Se trata de matrices simétricas cuadradas indexadas por los vértices, con el peso de vértice en el coeficiente diagonal y con el peso de arista en los coeficientes fuera de diagonal y . Cuando los vértices y no son adyacentes, se requiere que el coeficiente sea cero. Esta invariante es como máximo tres si y sólo si la gráfica es plana . Como muestra Lovász, cuando el gráfico es poliédrico, se puede obtener una representación del mismo como un poliedro encontrando una matriz de adyacencia ponderada de corank tres, encontrando tres vectores que formen una base para su espacio nulo , usando los coeficientes de estos vectores como coordenadas para el vértices de un poliedro y escalar estos vértices adecuadamente. [45]
La historia del teorema de Steinitz es descrita por Grünbaum (2007), [46] quien señala su primera aparición de forma críptica en una publicación de Ernst Steinitz , escrita originalmente en 1916. [6] Steinitz proporcionó más detalles en notas de conferencias posteriores, publicadas después de su muerte en 1928. Aunque los tratamientos modernos del teorema de Steinitz lo establecen como una caracterización teórica de grafos de los poliedros, Steinitz no utilizó el lenguaje de los grafos. [46] La formulación teórica de grafos del teorema fue introducida a principios de la década de 1960 por Branko Grünbaum y Theodore Motzkin , y su demostración también se convirtió a la teoría de grafos en el texto de Grünbaum de 1967 Convex Polytopes . [46] El trabajo de Epifanov sobre las transformaciones ΔY- e YΔ , fortaleciendo la prueba de Steinitz, fue motivado por otros problemas además de la caracterización de los poliedros. Truemper (1989) atribuye a Grünbaum la observación de la relevancia de este trabajo para el teorema de Steinitz. [11]
La correspondencia de Maxwell-Cremona entre diagramas de tensiones y elevaciones poliédricas fue desarrollada en una serie de artículos de James Clerk Maxwell de 1864 a 1870, basada en trabajos anteriores de Pierre Varignon , William Rankine y otros, y fue popularizada a finales del siglo XIX por Luis Cremona . [47] La observación de que esta correspondencia se puede utilizar con la incrustación de Tutte para demostrar el teorema de Steinitz proviene de Eades y Garvan (1995); [4] véase también Richter-Gebert (1996). [38]
El teorema del empaquetamiento circular fue demostrado por Paul Koebe en 1936 [48] [49] y (de forma independiente) por EM Andreev en 1970; [49] [50] fue popularizado a mediados de la década de 1980 por William Thurston , a quien (a pesar de citar a Koebe y Andreev) a menudo se le atribuye el mérito de ser uno de sus descubridores. [49] La versión de Andreev del teorema ya estaba formulada como una caracterización similar a la de Steinitz para ciertos poliedros en el espacio hiperbólico , [50] y el uso del empaquetamiento de círculos para realizar poliedros con esferas medias proviene del trabajo de Thurston. [51] El problema de caracterizar poliedros con esferas inscritas o circunscritas, finalmente resuelto utilizando un método basado en realizaciones de empaquetamiento de círculos, se remonta a trabajos inéditos de René Descartes alrededor de 1630 [52] y a Jakob Steiner en 1832; [35] [53] Los primeros ejemplos de poliedros que no tienen realización con una circunsfera o inesfera fueron dados por Steinitz en 1928. [35] [54]
Abgeschlossen am 31 de agosto de 1916