La emisión de electrones de campo , también conocida como emisión de campo ( FE ) y emisión de campo de electrones , es la emisión de electrones inducida por un campo electrostático . El contexto más común es la emisión de campo desde una superficie sólida al vacío . Sin embargo, la emisión de campo puede tener lugar desde superficies sólidas o líquidas , al vacío, un fluido (por ejemplo , aire ) o cualquier dieléctrico no conductor o débilmente conductor . La promoción inducida por campo de electrones desde la banda de valencia a la banda de conducción de semiconductores (el efecto Zener ) también puede considerarse una forma de emisión de campo. La terminología es histórica porque los fenómenos relacionados de fotoefecto de superficie, emisión termoiónica (o efecto Richardson-Dushman ) y "emisión electrónica fría", es decir, la emisión de electrones en campos eléctricos estáticos (o cuasiestáticos) fuertes, se descubrieron y estudiaron de forma independiente desde la década de 1880 hasta la de 1930. Cuando se utiliza emisión de campo sin calificadores, normalmente significa "emisión fría".
La emisión de campo en metales puros se produce en campos eléctricos intensos : los gradientes suelen ser superiores a 1 gigavoltio por metro y dependen en gran medida de la función de trabajo . Si bien las fuentes de electrones basadas en la emisión de campo tienen varias aplicaciones, la emisión de campo suele ser una fuente primaria indeseable de fenómenos de ruptura del vacío y descarga eléctrica , que los ingenieros tratan de evitar. Entre los ejemplos de aplicaciones de la emisión de campo superficial se incluyen la construcción de fuentes de electrones brillantes para microscopios electrónicos de alta resolución o la descarga de cargas inducidas desde naves espaciales . Los dispositivos que eliminan las cargas inducidas se denominan neutralizadores de carga .
La emisión de campo se explicó mediante el efecto túnel cuántico de los electrones a finales de la década de 1920. Este fue uno de los triunfos de la naciente mecánica cuántica . La teoría de la emisión de campo de los metales a granel fue propuesta por Ralph H. Fowler y Lothar Wolfgang Nordheim . [1] Una familia de ecuaciones aproximadas, las ecuaciones de Fowler-Nordheim, lleva su nombre. Estrictamente, las ecuaciones de Fowler-Nordheim se aplican solo a la emisión de campo de los metales a granel y (con la modificación adecuada) a otros sólidos cristalinos a granel , pero a menudo se utilizan, como una aproximación aproximada, para describir la emisión de campo de otros materiales.
Emisión de electrones de campo , emisión de electrones inducida por campo , emisión de campo y emisión de electrones de campo son nombres generales para este fenómeno experimental y su teoría. Aquí se utiliza el primer nombre.
El efecto túnel de Fowler-Nordheim es el efecto túnel ondulatorio de los electrones a través de una barrera triangular redondeada creada en la superficie de un conductor de electrones mediante la aplicación de un campo eléctrico muy alto. Mediante el efecto túnel de Fowler-Nordheim, los electrones individuales pueden escapar de muchos materiales en diversas circunstancias diferentes.
La emisión de electrones en campo frío (CFE) es el nombre que se le da a un régimen de emisión estadística particular, en el que los electrones en el emisor están inicialmente en equilibrio termodinámico interno , y en el que la mayoría de los electrones emitidos escapan por efecto túnel de Fowler-Nordheim desde estados electrónicos cercanos al nivel de Fermi del emisor . (Por el contrario, en el régimen de emisión de Schottky , la mayoría de los electrones escapan por encima de una barrera de campo reducido, desde estados muy por encima del nivel de Fermi). Muchos materiales sólidos y líquidos pueden emitir electrones en un régimen CFE si se aplica un campo eléctrico de un tamaño apropiado.
Las ecuaciones de tipo Fowler-Nordheim son una familia de ecuaciones aproximadas derivadas para describir la emisión de campo electromagnético a partir de los estados electrónicos internos en metales a granel. Los diferentes miembros de la familia representan diferentes grados de aproximación a la realidad. Las ecuaciones aproximadas son necesarias porque, para los modelos físicamente realistas de la barrera de efecto túnel, es matemáticamente imposible en principio resolver la ecuación de Schrödinger de manera exacta y sencilla. No hay ninguna razón teórica para creer que las ecuaciones de tipo Fowler-Nordheim describan de manera válida la emisión de campo de materiales distintos de los sólidos cristalinos a granel.
En el caso de los metales, el régimen de emisión electroquímica se extiende hasta temperaturas muy superiores a la temperatura ambiente. Existen otros regímenes de emisión de electrones (como la " emisión térmica de electrones " y la " emisión Schottky ") que requieren un calentamiento externo significativo del emisor. También existen regímenes de emisión en los que los electrones internos no están en equilibrio termodinámico y la corriente de emisión está determinada, en parte o en su totalidad, por el suministro de electrones a la región emisora. Un proceso de emisión de no equilibrio de este tipo puede denominarse emisión de campo (electrones) si la mayoría de los electrones escapan por efecto túnel, pero estrictamente no es una emisión electroquímica y no se describe con precisión mediante una ecuación de tipo Fowler-Nordheim.
Es necesario tener cuidado porque en algunos contextos (por ejemplo, ingeniería espacial), el nombre "emisión de campo" se aplica a la emisión de iones inducida por el campo (emisión de iones de campo), en lugar de electrones, y porque en algunos contextos teóricos "emisión de campo" se utiliza como un nombre general que abarca tanto la emisión de electrones de campo como la emisión de iones de campo.
Históricamente, el fenómeno de emisión de electrones de campo se ha conocido por una variedad de nombres, incluidos "efecto aeona", "emisión autoelectrónica", "emisión fría", "emisión de cátodo frío", "emisión de campo", "emisión de electrones de campo" y "emisión de campo de electrones".
Las ecuaciones de este artículo se escriben utilizando el Sistema Internacional de Cantidades (ISQ). Este es el sistema internacional moderno (posterior a la década de 1970), basado en el sistema de ecuaciones racionalizado metro-kilogramo-segundo (rmks), que se utiliza para definir las unidades del SI. La literatura más antigua sobre emisión de campo (y los artículos que copian directamente ecuaciones de la literatura antigua) a menudo escriben algunas ecuaciones utilizando un sistema de ecuaciones más antiguo que no utiliza la cantidad ε 0 . En este artículo, todas esas ecuaciones se han convertido a la forma internacional moderna. Para mayor claridad, esto siempre debe hacerse.
Dado que la función de trabajo se expresa normalmente en electronvoltios (eV) y suele ser conveniente medir los campos en voltios por nanómetro (V/nm), los valores de la mayoría de las constantes universales se expresan aquí en unidades que incluyen eV, V y nm. Esta es una práctica cada vez más habitual en la investigación sobre emisiones de campo. Sin embargo, todas las ecuaciones que se presentan aquí son compatibles con ISQ y mantienen su coherencia dimensional, tal como lo exige el sistema internacional moderno. Para indicar su estado, los valores numéricos de las constantes universales se expresan con siete cifras significativas. Los valores se derivan utilizando los valores de 2006 de las constantes fundamentales.
La emisión de electrones de campo tiene una historia larga, complicada y confusa. Esta sección cubre los primeros pasos hasta la derivación de la ecuación original de tipo Fowler-Nordheim en 1928.
En retrospectiva, parece probable que las descargas eléctricas descritas por JH Winkler [2] en 1744 fueran iniciadas por CFE desde su electrodo de alambre. Sin embargo, las investigaciones significativas tuvieron que esperar hasta después de la identificación del electrón por JJ Thomson [3] en 1897, y hasta después de que se entendiera - a partir del trabajo de emisión térmica [4] y fotoemisión [5] - que los electrones podían emitirse desde el interior de los metales (en lugar de desde moléculas de gas adsorbidas en la superficie ), y que - en ausencia de campos aplicados - los electrones que escapaban de los metales tenían que superar una barrera de función de trabajo.
Ya en 1913 se sospechaba que la emisión inducida por el campo era un efecto físico independiente. [6] Sin embargo, esto sólo se estableció con certeza después de que las técnicas de limpieza de muestras y de vacío hubieran mejorado significativamente. Lilienfeld (que estaba principalmente interesado en las fuentes de electrones para aplicaciones médicas de rayos X ) publicó en 1922 [7] el primer relato claro en inglés de la fenomenología experimental del efecto que había llamado "emisión autoelectrónica". Había trabajado en este tema, en Leipzig, desde aproximadamente 1910. Kleint describe este y otros trabajos tempranos. [8] [9]
Después de 1922, el interés experimental aumentó, particularmente en los grupos dirigidos por Millikan en el Instituto de Tecnología de California (Caltech) en Pasadena, California , [10] y por Gossling en la General Electric Company en Londres. [11] Los intentos de comprender la emisión autoelectrónica incluyeron graficar datos experimentales de corriente-voltaje ( i–V ) de diferentes maneras, para buscar una relación en línea recta. La corriente aumentó con el voltaje más rápidamente que linealmente, pero los gráficos de tipo log( i ) vs. V no fueron rectos. [10] Walter H. Schottky [12] sugirió en 1923 que el efecto podría deberse a la emisión inducida térmicamente sobre una barrera de campo reducido. Si es así, entonces los gráficos de log( i ) vs. √ V deberían ser rectos, pero no lo fueron. [10] La explicación de Schottky tampoco es compatible con la observación experimental de una dependencia de la temperatura muy débil en la CFE [7] , un punto que inicialmente se pasó por alto. [6]
Un gran avance se produjo cuando CC Lauritsen [13] (y J. Robert Oppenheimer de forma independiente [14] ) descubrieron que los gráficos de log( i ) frente a 1/ V producían buenas líneas rectas. Este resultado, publicado por Millikan y Lauritsen [13] a principios de 1928, era conocido por Fowler y Nordheim .
Oppenheimer había predicho [14] que la tunelización inducida por el campo de los electrones de los átomos (el efecto ahora llamado ionización de campo) tendría esta dependencia i ( V ), había encontrado esta dependencia en los resultados experimentales de emisión de campo publicados de Millikan y Eyring, [10] y propuso que la CFE se debía a la tunelización inducida por el campo de los electrones de los orbitales similares a los atómicos en los átomos metálicos de la superficie. Una teoría alternativa de Fowler-Nordheim [1] explicaba tanto el hallazgo de Millikan-Lauritsen como la dependencia muy débil de la corriente con la temperatura. La teoría de Fowler-Nordheim predijo que ambas serían consecuencias si la CFE se debía a la tunelización inducida por el campo de los estados de tipo electrón libre en lo que ahora llamaríamos una banda de conducción metálica , con los estados de los electrones ocupados de acuerdo con las estadísticas de Fermi-Dirac .
Los detalles matemáticos de la teoría de Oppenheimer eran seriamente incorrectos. [15] También había un pequeño error numérico en la ecuación final dada por la teoría de Fowler-Nordheim para la densidad de corriente de CFE : esto fue corregido en el artículo de 1929 de (Stern, Gossling y Fowler 1929). [16]
Estrictamente, si el campo de barrera en la teoría de Fowler-Nordheim de 1928 es exactamente proporcional al voltaje aplicado, y si el área de emisión es independiente del voltaje, entonces la teoría de Fowler-Nordheim de 1928 predice que los gráficos de la forma (log( i / V 2 ) vs. 1/ V ) deberían ser líneas rectas exactas. Sin embargo, las técnicas experimentales contemporáneas no fueron lo suficientemente buenas para distinguir entre el resultado teórico de Fowler-Nordheim y el resultado experimental de Millikan-Lauritsen.
De este modo, en 1928 se había logrado una comprensión física básica del origen de la CFE a partir de metales a granel, y se había derivado la ecuación original de tipo Fowler-Nordheim.
La literatura a menudo presenta el trabajo de Fowler-Nordheim como una prueba de la existencia del efecto túnel de electrones , como lo predice la mecánica ondulatoria. Si bien esto es correcto, la validez de la mecánica ondulatoria fue ampliamente aceptada en 1928. El papel más importante del artículo de Fowler-Nordheim fue que fue un argumento convincente a partir del experimento de que las estadísticas de Fermi-Dirac se aplicaban al comportamiento de los electrones en metales, como lo sugirió Sommerfeld [17] en 1927. El éxito de la teoría de Fowler-Nordheim hizo mucho para apoyar la corrección de las ideas de Sommerfeld y ayudó en gran medida a establecer la teoría moderna de bandas de electrones . [18] En particular, la ecuación original de tipo Fowler-Nordheim fue una de las primeras en incorporar las consecuencias estadístico-mecánicas de la existencia del espín electrónico en la teoría de un efecto experimental de materia condensada. El artículo de Fowler-Nordheim también estableció la base física para un tratamiento unificado de la emisión de electrones inducida por campo e inducida térmicamente . [18] Antes de 1928 se había planteado la hipótesis de que en los metales existían dos tipos de electrones, los "termiones" y los "electrones de conducción", y que las corrientes de electrones emitidas térmicamente se debían a la emisión de termiones, pero que las corrientes emitidas por el campo se debían a la emisión de electrones de conducción. El trabajo de Fowler-Nordheim de 1928 sugería que los termiones no necesitaban existir como una clase separada de electrones internos: los electrones podían provenir de una única banda ocupada de acuerdo con las estadísticas de Fermi-Dirac, pero se emitirían de formas estadísticamente diferentes en diferentes condiciones de temperatura y campo aplicado.
Las ideas de Oppenheimer , Fowler y Nordheim también fueron un estímulo importante para el desarrollo, por George Gamow , [19] y Ronald W. Gurney y Edward Condon , [20] [21] más tarde en 1928, de la teoría de la desintegración radiactiva de los núcleos (por efecto túnel de partículas alfa ). [22]
Como ya se ha indicado, los primeros trabajos experimentales sobre emisión de electrones de campo (1910-1920) [7] fueron impulsados por el deseo de Lilienfeld de desarrollar tubos de rayos X miniaturizados para aplicaciones médicas. Sin embargo, era demasiado pronto para que esta tecnología tuviera éxito.
Después del trabajo teórico de Fowler-Nordheim en 1928, un avance importante llegó con el desarrollo en 1937 por Erwin W. Mueller del microscopio electrónico de campo de geometría esférica (FEM) [23] (también llamado "microscopio de emisión de campo"). En este instrumento, el emisor de electrones es un alambre puntiagudo, de radio de vértice r . Este se coloca, en un recinto de vacío, frente a un detector de imagen (originalmente una pantalla de fósforo), a una distancia R de él. La pantalla del microscopio muestra una imagen de proyección de la distribución de la densidad de corriente J a través del vértice del emisor, con un aumento aproximado ( R / r ), típicamente 10 5 a 10 6 . En los estudios FEM, el radio del vértice es típicamente de 100 nm a 1 μm. La punta del alambre puntiagudo, cuando se hace referencia a él como un objeto físico, se ha llamado "emisor de campo", "punta" o (recientemente) "emisor de Mueller".
Cuando la superficie del emisor está limpia, esta imagen FEM es característica de: (a) el material del que está hecho el emisor; (b) la orientación del material en relación con el eje de la aguja/alambre; y (c) en cierta medida, la forma del extremo del emisor. En la imagen FEM, las áreas oscuras corresponden a regiones donde la función de trabajo local φ es relativamente alta y/o el campo de barrera local F es relativamente bajo, por lo que J es relativamente bajo; las áreas claras corresponden a regiones donde φ es relativamente bajo y/o F es relativamente alto, por lo que J es relativamente alto. Esto es como lo predice el exponente de las ecuaciones de tipo Fowler-Nordheim [ver ecuación (30) a continuación].
La adsorción de capas de átomos de gas (como el oxígeno) sobre la superficie del emisor, o parte de ella, puede crear dipolos eléctricos superficiales que cambian la función de trabajo local de esta parte de la superficie. Esto afecta a la imagen FEM; también, el cambio de la función de trabajo se puede medir utilizando un gráfico de Fowler-Nordheim (ver más abajo). Por lo tanto, el FEM se convirtió en una herramienta de observación temprana de la ciencia de superficies . [24] [25] Por ejemplo, en la década de 1960, los resultados del FEM contribuyeron significativamente a las discusiones sobre catálisis heterogénea . [26] El FEM también se ha utilizado para estudios de difusión de átomos de superficie . Sin embargo, ahora el FEM ha sido reemplazado casi por completo por técnicas de ciencia de superficies más nuevas.
Una consecuencia del desarrollo del método de elementos finitos y la experimentación posterior fue que se hizo posible identificar (a partir de la inspección de imágenes del método de elementos finitos) cuándo un emisor estaba "limpio" y, por lo tanto, exhibía su función de trabajo de superficie limpia, como se estableció mediante otras técnicas. Esto fue importante en experimentos diseñados para probar la validez de la ecuación estándar de tipo Fowler-Nordheim. [27] [28] Estos experimentos dedujeron un valor del factor de conversión de voltaje a campo de barrera β a partir de un gráfico de Fowler-Nordheim (ver más abajo), asumiendo el valor φ de superficie limpia para el tungsteno, y lo compararon con valores derivados de observaciones con microscopio electrónico de la forma del emisor y el modelado electrostático. Se logró una concordancia de aproximadamente el 10%. Sólo muy recientemente [29] ha sido posible hacer la comparación a la inversa, acercando una sonda bien preparada a una superficie bien preparada de manera que se pueda suponer una geometría aproximada de placas paralelas y el factor de conversión se pueda tomar como 1/ W , donde W es la separación medida entre la sonda y el emisor. El análisis del gráfico de Fowler-Nordheim resultante arroja un valor de función de trabajo cercano a la función de trabajo conocida independientemente del emisor.
Las mediciones de distribución de energía de los electrones emitidos por el campo se informaron por primera vez en 1939. [30] En 1959, Young [31] se dio cuenta teóricamente y Young y Mueller [32] lo confirmaron experimentalmente que la cantidad medida en geometría esférica era la distribución de la energía total del electrón emitido (su "distribución de energía total"). Esto se debe a que, en geometría esférica, los electrones se mueven de tal manera que el momento angular alrededor de un punto en el emisor se conserva casi por completo. Por lo tanto, cualquier energía cinética que, en la emisión, esté en una dirección paralela a la superficie del emisor se convierte en energía asociada con la dirección radial del movimiento. Por lo tanto, lo que se mide en un analizador de energía es la energía total en la emisión.
Con el desarrollo de analizadores de energía de electrones sensibles en la década de 1960, se hizo posible medir detalles finos de la distribución total de energía. Estos reflejan detalles finos de la física de la superficie , y la técnica de espectroscopia de electrones de campo floreció por un tiempo, antes de ser reemplazada por técnicas más nuevas de ciencia de superficies. [33] [34]

Para lograr una alta resolución en microscopios electrónicos y otros instrumentos de haz de electrones (como los utilizados para la litografía por haz de electrones ), es útil comenzar con una fuente de electrones que sea pequeña, ópticamente brillante y estable. Las fuentes basadas en la geometría de un emisor de Mueller califican bien en los primeros dos criterios. La primera observación de un átomo individual con microscopio electrónico (EM) fue realizada por Crewe, Wall y Langmore en 1970, [35] utilizando un microscopio electrónico de barrido equipado con un cañón de emisión de campo temprano.
Desde la década de 1950 en adelante, se ha dedicado un gran esfuerzo al desarrollo de fuentes de emisión de campo para su uso en cañones de electrones . [36] [37] [38] [por ejemplo, DD53] Se han desarrollado métodos para generar haces sobre el eje, ya sea mediante la acumulación de emisores inducidos por campo o mediante la deposición selectiva de un adsorbato de baja función de trabajo (generalmente óxido de circonio - ZrO) en el vértice plano de un emisor de tungsteno orientado (100) . [39]
Las fuentes que funcionan a temperatura ambiente tienen la desventaja de que se cubren rápidamente con moléculas adsorbidas que llegan desde las paredes del sistema de vacío , y el emisor debe limpiarse de vez en cuando "calentándolo" a alta temperatura. Hoy en día, es más común utilizar fuentes basadas en emisores de Mueller que funcionan a temperaturas elevadas, ya sea en el régimen de emisión Schottky o en el llamado régimen intermedio de campo de temperatura. Muchos microscopios electrónicos de alta resolución e instrumentos de haz de electrones modernos utilizan alguna forma de fuente de electrones basada en emisores de Mueller. Actualmente, se están realizando intentos para desarrollar nanotubos de carbono (CNT) como fuentes de emisión de campo de cañón de electrones. [40] [41]
El uso de fuentes de emisión de campo en instrumentos ópticos electrónicos ha implicado el desarrollo de teorías apropiadas de óptica de partículas cargadas, [37] [42] y el desarrollo de modelos relacionados. Se han probado varios modelos de forma para emisores de Mueller; el mejor parece ser el modelo "Esfera sobre cono ortogonal" (SOC) introducido por Dyke, Trolan, Dolan y Barnes en 1953. [43] Wiesener y Everhart realizaron simulaciones importantes, que involucraban el rastreo de trayectorias utilizando el modelo de emisor SOC. [44] [45] [46] Hoy en día, la capacidad de simular la emisión de campo de los emisores de Mueller a menudo se incorpora a los programas comerciales de óptica electrónica que se utilizan para diseñar instrumentos de haz de electrones. El diseño de cañones de electrones de emisión de campo modernos y eficientes requiere conocimientos altamente especializados.
Hoy en día es posible preparar emisores muy nítidos, incluidos emisores que terminan en un solo átomo. En este caso, la emisión de electrones proviene de un área de aproximadamente el doble del tamaño cristalográfico de un solo átomo. Esto se demostró comparando imágenes del emisor obtenidas con microscopios de iones de campo (FIM) y de elementos finitos (FEM). [47] Los emisores de Mueller de un solo átomo con ápice también son relevantes para la microscopía de sonda de barrido y la microscopía de iones de barrido de helio (He SIM). [48] Las técnicas para prepararlos han estado bajo investigación durante muchos años. [47] [49] Un avance reciente importante relacionado ha sido el desarrollo (para su uso en el He SIM) de una técnica automatizada para restaurar un ápice de tres átomos ("trímero") a su estado original, si el trímero se rompe. [48]
Las fuentes de emisión de campo de gran superficie han suscitado interés desde los años 70. En estos dispositivos se crea una alta densidad de puntos de emisión de campo individuales sobre un sustrato (originalmente silicio). Esta área de investigación se conoció primero como "microelectrónica de vacío" y ahora como "nanoelectrónica de vacío".
Uno de los dos tipos de dispositivos originales, el " conjunto Spindt ", [50] utilizaba técnicas de fabricación de circuitos integrados (CI) de silicio para crear conjuntos regulares en los que se depositaban conos de molibdeno en pequeños huecos cilíndricos en una película de óxido, con el hueco cubierto por un contraelectrodo con una abertura circular central. Esta geometría general también se ha utilizado con nanotubos de carbono cultivados en el hueco.
El otro tipo de dispositivo original fue el "emisor Latham". [51] [52] Se trataba de dispositivos MIMIV (metal-aislante-metal-aislante-vacío) o, de forma más general, CDCDV (conductor-dieléctrico-conductor-dieléctrico-vacío) que contenían partículas conductoras en una película dieléctrica. El dispositivo emite campos porque su microestructura/nanoestructura tiene propiedades de mejora del campo. Este material tenía una ventaja potencial de producción, ya que podía depositarse como una "tinta", por lo que no se necesitaban técnicas de fabricación de circuitos integrados. Sin embargo, en la práctica, resultó difícil fabricar dispositivos uniformemente fiables.
La investigación avanzó en la búsqueda de otros materiales que pudieran depositarse o desarrollarse como películas delgadas con propiedades adecuadas para mejorar el campo. En una disposición de placas paralelas, el campo "macroscópico" F M entre las placas está dado por F M = V / W , donde W es la separación de las placas y V es el voltaje aplicado. Si se crea un objeto afilado en una placa, entonces el campo local F en su vértice es mayor que F M y se puede relacionar con F M mediante
El parámetro γ se denomina "factor de mejora del campo" y está determinado básicamente por la forma del objeto. Dado que las características de emisión del campo están determinadas por el campo local F , cuanto mayor sea el valor γ del objeto, menor será el valor de F M en el que se produce una emisión significativa. Por lo tanto, para un valor dado de W , menor será el voltaje aplicado V en el que se produce una emisión significativa.
Durante un período de aproximadamente diez años desde mediados de la década de 1990, hubo un gran interés en la emisión de campo de películas de carbono amorfo y "similar al diamante" depositadas con plasma . [53] [54] Sin embargo, el interés disminuyó posteriormente, en parte debido a la llegada de los emisores de CNT y en parte porque surgió evidencia de que los sitios de emisión podrían estar asociados con objetos de carbono particulado creados de una manera desconocida durante el proceso de deposición : esto sugirió que el control de calidad de un proceso de producción a escala industrial podría ser problemático.
La introducción de los emisores de campo de CNT, [41] tanto en forma de "mat" como en forma de "conjunto crecido", fue un avance significativo. Se han llevado a cabo investigaciones exhaustivas tanto sobre sus características físicas como sobre sus posibles aplicaciones tecnológicas. [40] Para la emisión de campo, una ventaja de los CNT es que, debido a su forma, con su alta relación de aspecto , son "objetos naturales que mejoran el campo".
En los últimos años también ha habido un crecimiento masivo en el interés por el desarrollo de otras formas de emisores de película delgada, tanto los basados en otras formas de carbono (como "nanoparedes de carbono [55] ") como en varias formas de semiconductores de banda ancha. [56] Un objetivo particular es desarrollar nanoestructuras de "alta γ " con una densidad suficientemente alta de sitios de emisión individuales. Las películas delgadas de nanotubos en forma de redes de nanotubos también se utilizan para el desarrollo de electrodos de emisión de campo. [57] [58] [59] Se muestra que al ajustar con precisión los parámetros de fabricación, estas redes pueden lograr una densidad óptima de sitios de emisión individuales. [57] Se ha demostrado que los electrodos de doble capa hechos por deposición de dos capas de estas redes con alineación perpendicular entre sí pueden reducir el campo eléctrico de encendido (campo eléctrico requerido para lograr una corriente de emisión de 10 μA/cm 2 ) hasta 0,3 V/μm y proporcionar un rendimiento de emisión de campo estable. [58]
Un problema común con todos los dispositivos de emisión de campo, particularmente aquellos que operan en "condiciones de vacío industriales", es que el rendimiento de emisión puede degradarse por la adsorción de átomos de gas que llegan desde otras partes del sistema, y la forma del emisor puede, en principio, modificarse de manera perjudicial por una variedad de procesos secundarios no deseados, como el bombardeo de iones creados por el impacto de los electrones emitidos sobre átomos en fase gaseosa y/o sobre la superficie de los contraelectrodos. Por lo tanto, un requisito industrial importante es la "robustez en malas condiciones de vacío"; esto debe tenerse en cuenta en la investigación sobre nuevos materiales para emisores.
Al momento de escribir este artículo, las formas más prometedoras de fuente de emisión de campo de área grande (ciertamente en términos de densidad de corriente de emisión promedio lograda) parecen ser los conjuntos Spindt y las diversas formas de fuente basadas en CNT.
El desarrollo de fuentes de emisión de campo de gran superficie fue impulsado originalmente por el deseo de crear formas nuevas y más eficientes de visualización de información electrónica . Estas se conocen como " pantallas de emisión de campo " o "pantallas nanoemisoras". Aunque se han demostrado varios prototipos, [40] el desarrollo de dichas pantallas en productos comerciales confiables se ha visto obstaculizado por una variedad de problemas de producción industrial no relacionados directamente con las características de la fuente [En08].
Otras aplicaciones propuestas para fuentes de emisión de campo de área grande [40] incluyen la generación de microondas , la neutralización de vehículos espaciales, la generación de rayos X y (para fuentes de matriz) la litografía de múltiples haces de electrones . También hay intentos recientes de desarrollar emisores de área grande sobre sustratos flexibles, en línea con tendencias más amplias hacia la " electrónica plástica ".
El desarrollo de tales aplicaciones es la misión de la nanoelectrónica de vacío. Sin embargo, los emisores de campo funcionan mejor en condiciones de buen vacío ultraalto. Sus aplicaciones más exitosas hasta la fecha (FEM, FES y cañones EM) se han producido en estas condiciones. El triste hecho es que los emisores de campo y las condiciones de vacío industrial no se llevan bien juntos, y los problemas relacionados con garantizar de manera confiable una buena "robustez al vacío" de las fuentes de emisión de campo utilizadas en tales condiciones aún esperan mejores soluciones (probablemente soluciones de materiales más inteligentes) que las que tenemos actualmente.
Como ya se ha indicado, ahora se piensa que las primeras manifestaciones de la emisión de electrones de campo fueron las descargas eléctricas que causó. Después del trabajo de Fowler-Nordheim, se entendió que la CFE era una de las posibles causas subyacentes primarias de la ruptura del vacío y los fenómenos de descarga eléctrica. (Los mecanismos y vías detalladas involucradas pueden ser muy complicadas, y no hay una única causa universal) [60] Cuando se sabe que la ruptura del vacío es causada por la emisión de electrones desde un cátodo, entonces la idea original era que el mecanismo era la CFE de pequeñas protuberancias superficiales conductoras en forma de aguja. Se utilizaron (y se utilizan) procedimientos para redondear y suavizar las superficies de los electrodos que podrían generar corrientes de emisión de electrones de campo no deseadas. Sin embargo, el trabajo de Latham y otros [51] mostró que la emisión también podría estar asociada con la presencia de inclusiones semiconductoras en superficies lisas. La física de cómo se genera la emisión aún no se entiende completamente, pero existe la sospecha de que pueden estar involucrados los llamados "efectos de triple unión". Se puede encontrar más información en el libro de Latham [51] y en la bibliografía en línea. [60]
En algunos dispositivos electrónicos, la transferencia de electrones de un material a otro, o (en el caso de bandas inclinadas) de una banda a otra (" efecto túnel Zener "), se produce mediante un proceso de efecto túnel inducido por el campo que puede considerarse como una forma de efecto túnel de Fowler-Nordheim. Por ejemplo, el libro de Rhoderick analiza la teoría pertinente a los contactos metal-semiconductor . [61]
La siguiente parte de este artículo trata de la teoría básica de la emisión de electrones en campos fríos a partir de metales en masa. La mejor manera de abordarla es en cuatro etapas principales, que incluyen la teoría asociada con: (1) la derivación de una fórmula para la " probabilidad de escape ", considerando el efecto túnel de los electrones a través de una barrera triangular redondeada; (2) una integración sobre los estados electrónicos internos para obtener la "distribución total de energía"; (3) una segunda integración, para obtener la densidad de corriente de emisión como una función del campo de barrera local y la función de trabajo local; (4) la conversión de esto a una fórmula para la corriente como una función del voltaje aplicado. Las ecuaciones modificadas necesarias para emisores de área grande y las cuestiones del análisis de datos experimentales se tratan por separado.
El efecto túnel de Fowler-Nordheim es el efecto túnel ondulatorio de un electrón a través de una barrera triangular exacta o redondeada. Se reconocen dos situaciones básicas: (1) cuando el electrón está inicialmente en un estado localizado ; (2) cuando el electrón no está inicialmente fuertemente localizado, y se representa mejor mediante una onda viajera . La emisión desde una banda de conducción de metal en masa es una situación del segundo tipo, y la discusión aquí se relaciona con este caso. También se supone que la barrera es unidimensional (es decir, no tiene estructura lateral) y no tiene una estructura a escala fina que cause efectos de " dispersión " o "resonancia". Para mantener esta explicación del efecto túnel de Fowler-Nordheim relativamente simple, se necesitan estas suposiciones; pero en efecto se está ignorando la estructura atómica de la materia.
Para un electrón, la ecuación unidimensional de Schrödinger se puede escribir en la forma
donde Ψ( x ) es la función de onda del electrón , expresada como una función de la distancia x medida desde la superficie eléctrica del emisor, [62] ħ es la constante de Planck reducida , m es la masa del electrón, U ( x ) es la energía potencial del electrón , E n es la energía total del electrón asociada con el movimiento en la dirección x , y M ( x ) = [ U ( x ) − E n ] se llama energía motriz del electrón. [63] M ( x ) puede interpretarse como el negativo de la energía cinética del electrón asociada con el movimiento de un electrón puntual clásico hipotético en la dirección x , y es positivo en la barrera.
La forma de una barrera de tunelización está determinada por cómo M ( x ) varía con la posición en la región donde M ( x ) > 0. Dos modelos tienen un estatus especial en la teoría de emisión de campo: la barrera triangular exacta (ET) y la barrera Schottky-Nordheim (SN) . [64] [65] Estas se dan por las ecuaciones (2) y (3), respectivamente:
Aquí h es la altura del campo cero (o altura no reducida ) de la barrera, e es la carga positiva elemental , F es el campo de la barrera y ε 0 es la constante eléctrica . Por convención, F se toma como positiva, aunque el campo electrostático clásico sería negativo. La ecuación SN utiliza la energía potencial de imagen clásica para representar el efecto físico "correlación e intercambio".
Para un electrón que se acerca a una barrera dada desde el interior, la probabilidad de escape (o " coeficiente de transmisión " o "coeficiente de penetración") es una función de h y F , y se denota por D ( h , F ). El objetivo principal de la teoría de efecto túnel es calcular D ( h , F ). Para modelos de barrera físicamente realistas, como la barrera de Schottky-Nordheim, la ecuación de Schrödinger no se puede resolver exactamente de ninguna manera simple. Se puede utilizar el siguiente enfoque llamado "semiclásico". Un parámetro G ( h , F ) se puede definir por la integral JWKB (Jeffreys-Wentzel-Kramers-Brillouin) : [66]
donde la integral se toma a través de la barrera (es decir, a través de la región donde M > 0), y el parámetro g es una constante universal dada por
Forbes ha reordenado un resultado demostrado por Fröman y Fröman, para mostrar que, formalmente – en un tratamiento unidimensional – la solución exacta para D puede escribirse [67]
donde el factor previo de tunelización P puede evaluarse en principio mediante integraciones iterativas complicadas a lo largo de una trayectoria en el espacio complejo . [67] [68] En el régimen CFE tenemos (por definición) G ≫ 1. Además, para modelos simples P ≈ 1. Por lo que la ecuación (6) se reduce a la denominada fórmula JWKB simple:
Para la barrera triangular exacta, al colocar la ecuación (2) en la ecuación (4) se obtiene G ET = bh 3/2 / F , donde
Este parámetro b es una constante universal a veces llamada segunda constante de Fowler-Nordheim . Para barreras de otras formas, escribimos
donde ν ( h , F ) es un factor de corrección que en general debe determinarse mediante integración numérica , utilizando la ecuación (4).
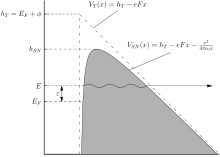
La barrera Schottky-Nordheim, que es el modelo de barrera utilizado para derivar la ecuación estándar de tipo Fowler-Nordheim, [69] es un caso especial. En este caso, se sabe que el factor de corrección es una función de una única variable f h , definida por f h = F / F h , donde F h es el campo necesario para reducir la altura de una barrera Schottky-Nordheim de h a 0. Este campo está dado por
El parámetro f h varía de 0 a 1 y puede denominarse campo de barrera escalado para una barrera de Schottky-Nordheim de altura de campo cero h .
Para la barrera Schottky-Nordheim, ν ( h , F ) viene dada por el valor particular ν ( f h ) de una función ν ( ℓ′ ). Esta última es una función de la física matemática por derecho propio y se la ha denominado función principal de barrera Schottky-Nordheim . En un artículo de 2008 de J. Deane se deriva una expansión de serie explícita para ν ( ℓ′ ). [70] Se ha encontrado la siguiente buena aproximación simple para ν ( f h ): [69]
El ancho de desintegración (en energía), d h , mide qué tan rápido disminuye la probabilidad de escape D a medida que aumenta la altura de la barrera h ; d h se define por:
Cuando h aumenta en d h entonces la probabilidad de escape D disminuye en un factor cercano a e ( ≈ 2,718282). Para un modelo elemental, basado en la barrera triangular exacta, donde ponemos ν = 1 y P ≈ 1, obtenemos
El ancho de decaimiento d h derivado de la expresión más general (12) difiere de éste por un "factor de corrección de ancho de decaimiento" λ d , por lo que:
Generalmente, el factor de corrección se puede aproximar a la unidad.
El ancho de decaimiento d F para una barrera con h igual a la función de trabajo local φ es de especial interés. Numéricamente, esto se da por:
Para los metales , el valor de d F suele ser del orden de 0,2 eV, pero varía con el campo de barrera F.
Es necesaria una nota histórica. La idea de que la barrera Schottky-Nordheim necesitaba un factor de corrección, como en la ecuación (9), fue introducida por Nordheim en 1928, [65] pero su análisis matemático del factor era incorrecto. Burgess, Kroemer y Houston introdujeron una nueva función ( correcta ) en 1953, y Murphy y Good desarrollaron sus matemáticas en 1956. [72] Esta función corregida, a veces conocida como "función elíptica de emisión de campo especial", se expresó como una función de una variable matemática y conocida como el "parámetro de Nordheim". Solo recientemente (2006 a 2008) se ha comprendido que, matemáticamente, es mucho mejor utilizar la variable ℓ′ ( = y 2 ) . Y sólo recientemente ha sido posible completar la definición de ν ( ℓ′ ) mediante el desarrollo y la prueba de la validez de una expansión en serie exacta para esta función (partiendo de soluciones conocidas de casos especiales de la ecuación diferencial hipergeométrica de Gauss ). Además, la aproximación (11) se ha encontrado sólo recientemente. La aproximación (11) supera, y presumiblemente eventualmente desplazará, a todas las aproximaciones anteriores de complejidad equivalente. Estos desarrollos recientes, y sus implicaciones, probablemente tendrán un impacto significativo en la investigación de emisión de campo a su debido tiempo.
El siguiente resumen reúne estos resultados. Para la construcción de un túnel muy por debajo de la parte superior de una barrera de altura razonable que se comporta bien, la probabilidad de escape D ( h , F ) se expresa formalmente mediante:
donde ν ( h , F ) es un factor de corrección que en general se debe encontrar por integración numérica. Para el caso especial de una barrera Schottky-Nordheim, existe un resultado analítico y ν ( h , F ) está dado por ν ( f h ), como se discutió anteriormente; la aproximación (11) para ν ( f h ) es más que suficiente para todos los propósitos tecnológicos. El pre-factor P también es en principio una función de h y (quizás) F , pero para los modelos físicos simples discutidos aquí es usualmente satisfactorio hacer la aproximación P = 1. La barrera triangular exacta es un caso especial donde la ecuación de Schrödinger se puede resolver exactamente, como lo hicieron Fowler y Nordheim; [1] para este caso físicamente poco realista, ν ( f h ) = 1, y existe una aproximación analítica para P.
El enfoque descrito aquí fue desarrollado originalmente para describir el efecto túnel de Fowler-Nordheim a partir de superficies emisoras lisas, clásicamente planas y planas. Es adecuado para superficies lisas, clásicamente curvas, con radios de hasta aproximadamente 10 a 20 nm. Se puede adaptar a superficies de radio más agudo, pero cantidades como ν y D se convierten entonces en funciones significativas de los parámetros utilizados para describir la curvatura de la superficie. Cuando el emisor es tan agudo que no se puede descuidar el detalle a nivel atómico, y/o la barrera de efecto túnel es más gruesa que las dimensiones del vértice del emisor, entonces es deseable un enfoque más sofisticado.
Como se señaló al principio, los efectos de la estructura atómica de los materiales no se tienen en cuenta en los tratamientos relativamente simples de la emisión de electrones de campo que se analizan aquí. Tener en cuenta la estructura atómica de forma adecuada es un problema muy difícil y solo se han logrado avances limitados. [33] Sin embargo, parece probable que las principales influencias en la teoría del efecto túnel de Fowler-Nordheim sean (en efecto) cambiar los valores de P y ν en la ecuación (15), en cantidades que no se pueden estimar fácilmente en la actualidad.
Todas estas observaciones se aplican en principio al efecto túnel de Fowler-Nordheim a partir de cualquier conductor en el que (antes del efecto túnel) los electrones pueden considerarse como si estuvieran en estados de ondas viajeras . El enfoque puede adaptarse para aplicarse (aproximadamente) a situaciones en las que los electrones se encuentran inicialmente en estados localizados en la superficie emisora o muy cerca de ella, pero esto queda fuera del alcance de este artículo.
La distribución de energía de los electrones emitidos es importante tanto para los experimentos científicos que utilizan la distribución de energía de los electrones emitidos para investigar aspectos de la física de la superficie del emisor [34] como para las fuentes de emisión de campo utilizadas en instrumentos de haz de electrones, como los microscopios electrónicos . [42] En el último caso, el "ancho" (en energía) de la distribución influye en la precisión con la que se puede enfocar el haz.
La explicación teórica aquí sigue el enfoque de Forbes. [73] Si ε denota la energía total del electrón relativa al nivel de Fermi del emisor, y K p denota la energía cinética del electrón paralela a la superficie del emisor, entonces la energía normal del electrón ε n (a veces llamada su "energía directa") se define por
Se reconocen dos tipos de distribución teórica de energía: la distribución de energía normal (NED), que muestra cómo se distribuye la energía ε n inmediatamente después de la emisión (es decir, inmediatamente fuera de la barrera de efecto túnel); y la distribución de energía total , que muestra cómo se distribuye la energía total ε . Cuando se utiliza el nivel de Fermi del emisor como nivel cero de referencia, tanto ε como ε n pueden ser positivos o negativos.
Desde la década de 1930 se han realizado experimentos de análisis de energía en emisores de campo. Sin embargo, recién a fines de la década de 1950 se descubrió (por Young y Mueller [31] [,YM58]) que estos experimentos siempre medían la distribución total de energía, que ahora se suele denotar por j ( ε ). Esto también es cierto (o casi cierto) cuando la emisión proviene de una pequeña protuberancia que mejora el campo en una superficie que de otro modo sería plana. [34]
Para ver cómo se puede calcular la distribución de energía total dentro del marco de un modelo de tipo electrón libre de Sommerfeld , observe el diagrama de energía-espacio PT (PT="parallel-total").
.jpg/440px-P-T_Energy_Space_(cropped).jpg)
Esto muestra la "energía cinética paralela" K p en el eje horizontal y la energía total ε en el eje vertical. Un electrón dentro del metal en masa generalmente tiene valores de K p y ε que se encuentran dentro del área ligeramente sombreada. Se puede demostrar que cada elemento d ε d K p de este espacio de energía hace una contribución a la densidad de corriente electrónica incidente en el interior del límite del emisor. [73] Aquí, z S es la constante universal (llamada aquí densidad de suministro de Sommerfeld ):
y es la función de distribución de Fermi-Dirac :
donde T es la temperatura termodinámica y k B es la constante de Boltzmann .
Este elemento de densidad de corriente incidente ve una barrera de altura h dada por:
La probabilidad de escape correspondiente es D ( h , F ): esta puede expandirse (aproximadamente) en la forma [73]
donde D F es la probabilidad de escape para una barrera de altura no reducida igual a la función de trabajo local φ . Por lo tanto, el elemento d ε d K p hace una contribución a la densidad de corriente de emisión, y la contribución total hecha por electrones incidentes con energías en el rango elemental d ε es entonces
donde la integral se toma en principio a lo largo de la franja que se muestra en el diagrama, pero en la práctica se puede extender hasta ∞ cuando el ancho de desintegración d F es mucho menor que la energía de Fermi K F (lo que siempre es el caso para un metal). El resultado de la integración se puede escribir:
donde y son valores apropiados para una barrera de altura no reducida h igual a la función de trabajo local φ , y se define mediante esta ecuación.
Para un emisor dado, con un campo dado aplicado a él, es independiente de F , por lo que la ecuación (21) muestra que la forma de la distribución (a medida que ε aumenta desde un valor negativo muy por debajo del nivel de Fermi) es una exponencial ascendente, multiplicada por la función de distribución FD. Esto genera la forma de distribución familiar predicha por primera vez por Young. [31] A bajas temperaturas, va bruscamente de 1 a 0 en la proximidad del nivel de Fermi, y la FWHM de la distribución está dada por:
El hecho de que las distribuciones experimentales de energía total de CFE tengan esta forma básica es una buena confirmación experimental de que los electrones en los metales obedecen a las estadísticas de Fermi-Dirac .
Las ecuaciones de tipo Fowler-Nordheim, en la forma J - F , son ecuaciones teóricas (aproximadas) derivadas para describir la densidad de corriente local J emitida desde los estados electrónicos internos en la banda de conducción de un metal en masa. La densidad de corriente de emisión (ECD) J para una pequeña región uniforme de una superficie emisora se expresa generalmente como una función J ( φ , F ) de la función de trabajo local φ y el campo de barrera local F que caracterizan la pequeña región. Para superficies con curvas pronunciadas, J también puede depender de los parámetros utilizados para describir la curvatura de la superficie.
Debido a las suposiciones físicas realizadas en la derivación original, [1] el término ecuación de tipo Fowler-Nordheim se ha utilizado durante mucho tiempo solo para ecuaciones que describen la ECD a temperatura cero. Sin embargo, es mejor permitir que este nombre incluya las ecuaciones ligeramente modificadas (que se analizan a continuación) que son válidas para temperaturas finitas dentro del régimen de emisión de CFE.
La densidad de corriente se mide mejor en A/m 2 . La densidad de corriente total emitida desde una pequeña región uniforme se puede obtener integrando la distribución de energía total j ( ε ) con respecto a la energía total de los electrones ε . A temperatura cero, la función de distribución de Fermi-Dirac f FD = 1 para ε <0, y f FD = 0 para ε >0. Por lo tanto, la ECD a 0 K, J 0 , se da a partir de la ecuación (18) por
donde es el suministro efectivo para el estado F , y se define mediante esta ecuación. Estrictamente, el límite inferior de la integral debería ser − K F , donde K F es la energía de Fermi ; pero si d F es mucho menor que K F (lo que siempre es el caso para un metal), entonces ninguna contribución significativa a la integral proviene de energías inferiores a K F , y se puede extender formalmente a –∞.
El resultado (23) puede interpretarse de manera física sencilla y útil consultando la figura 1. El estado del electrón en el punto "F" del diagrama ("estado F") es el "estado de movimiento hacia delante en el nivel de Fermi" (es decir, describe un electrón de nivel de Fermi que se mueve de manera normal hacia la superficie del emisor). A 0 K, un electrón en este estado ve una barrera de altura no reducida φ y tiene una probabilidad de escape D F que es mayor que la de cualquier otro estado ocupado del electrón. Por lo tanto, es conveniente escribir J 0 como Z F D F , donde el "suministro efectivo" Z F es la densidad de corriente que tendría que ser transportada por el estado F dentro del metal si toda la emisión saliera del estado F.
En la práctica, la densidad de corriente proviene principalmente de un grupo de estados cercanos en energía al estado F, la mayoría de los cuales se encuentran dentro del área muy sombreada en el diagrama de energía-espacio. Dado que, para un modelo de electrones libres , la contribución a la densidad de corriente es directamente proporcional al área en el espacio de energía (con la densidad de suministro de Sommerfeld z S como la constante de proporcionalidad), es útil pensar en la ECD como extraída de los estados de electrones en un área de tamaño d F 2 (medido en eV 2 ) en el diagrama de energía-espacio. Es decir, es útil pensar en la ECD como extraída de los estados en el área muy sombreada en la Fig. 1. (Esta aproximación empeora lentamente a medida que aumenta la temperatura).
Z F también se puede escribir en la forma:
donde la constante universal a , a veces llamada la Primera Constante de Fowler-Nordheim , viene dada por
Esto muestra claramente que el factor preexponencial a φ −1 F 2 , que aparece en las ecuaciones de tipo Fowler-Nordheim, se relaciona con el suministro efectivo de electrones a la superficie del emisor, en un modelo de electrones libres.
Para obtener un resultado válido para temperaturas distintas de cero, observamos en la ecuación (23) que z S d F D F = J 0 / d F . Por lo tanto, cuando la ecuación (21) se integra a temperaturas distintas de cero, entonces, al realizar esta sustitución e insertar la forma explícita de la función de distribución de Fermi-Dirac, la ECD J se puede escribir en la forma:
donde λ T es un factor de corrección de temperatura dado por la integral. La integral puede transformarse, escribiendo y , y luego , en el resultado estándar: [74]
Esto es válido para w > 1 (es decir, d F / k B T > 1). Por lo tanto, para temperaturas tales que k B T < d F :
donde la expansión es válida solo si (π k B T / d F ) ≪ 1. Un valor de ejemplo (para φ = 4,5 eV, F = 5 V/nm, T = 300 K) es λ T = 1,024. El pensamiento normal ha sido que, en el régimen CFE, λ T es siempre pequeño en comparación con otras incertidumbres, y que normalmente no es necesario incluirlo explícitamente en las fórmulas para la densidad de corriente a temperatura ambiente.
Los regímenes de emisión de los metales se definen, en la práctica, por los rangos de campo de barrera F y temperatura T para los cuales una familia dada de ecuaciones de emisión es matemáticamente adecuada. Cuando el campo de barrera F es lo suficientemente alto para que el régimen CFE funcione para la emisión de metales a 0 K, entonces la condición k B T < d F proporciona un límite superior formal (en temperatura) al régimen de emisión CFE. Sin embargo, se ha argumentado que (debido a aproximaciones realizadas en otras partes de la derivación) la condición k B T < 0,7 d F es un mejor límite de trabajo: esto corresponde a un valor λ T de alrededor de 1,09 y (para el caso de ejemplo) un límite superior de temperatura en el régimen CFE de alrededor de 1770 K. Este límite es una función del campo de barrera. [33] [72]
Nótese que el resultado (28) aquí se aplica para una barrera de cualquier forma (aunque d F será diferente para diferentes barreras).
El resultado (23) también conduce a cierta comprensión de lo que sucede cuando se tienen en cuenta los efectos a nivel atómico y la estructura de bandas ya no es como la de los electrones libres. Debido a la presencia de los núcleos iónicos atómicos, la barrera de superficie y también las funciones de onda de los electrones en la superficie serán diferentes. Esto afectará los valores del factor de corrección , el prefactor P y (hasta cierto punto) el factor de corrección λ d . Estos cambios, a su vez, afectarán los valores del parámetro D F y (hasta cierto punto) el parámetro d F . Para un metal real, la densidad de suministro variará con la posición en el espacio de energía, y el valor en el punto "F" puede ser diferente de la densidad de suministro de Sommerfeld. Podemos tener en cuenta este efecto introduciendo un factor de corrección de la estructura de bandas electrónicas λ B en la ecuación (23). Modinos ha discutido cómo se podría calcular este factor: estima que es más probable que esté entre 0,1 y 1; Puede estar fuera de estos límites, pero es muy poco probable que esté fuera del rango 0,01< λ B <10. [75]
Al definir un factor de corrección de la oferta global λ Z igual a λ T λ B λ d 2 , y combinar las ecuaciones anteriores, llegamos a la denominada ecuación de tipo Fowler-Nordheim físicamente completa: [76]
donde [= ( φ , F )] es el factor de corrección del exponente para una barrera de altura no reducida φ . Esta es la ecuación más general del tipo Fowler-Nordheim. Otras ecuaciones de la familia se obtienen sustituyendo expresiones específicas por los tres factores de corrección , P F y λ Z que contiene. La llamada ecuación elemental de tipo Fowler-Nordheim, que aparece en las discusiones de los libros de texto de pregrado sobre emisión de campo, se obtiene poniendo λ Z →1, P F →1, →1; esto no produce buenas predicciones cuantitativas porque hace que la barrera sea más fuerte de lo que es en la realidad física. La llamada ecuación estándar de tipo Fowler-Nordheim, desarrollada originalmente por Murphy y Good, [72] y muy utilizada en la literatura anterior, se obtiene poniendo λ Z → t F −2 , P F →1, → v F , donde v F es v ( f ), donde f es el valor de f h obtenido poniendo h = φ , y t F es un parámetro relacionado (de valor cercano a la unidad). [69]
Dentro de la teoría más completa descrita aquí, el factor t F −2 es una parte componente del factor de corrección λ d 2 [ver, [67] y notar que λ d 2 se denota por λ D allí]. No hay valor significativo en continuar la identificación separada de t F −2 . Probablemente, en el estado actual del conocimiento, la mejor aproximación para el modelado basado en ecuaciones de tipo Fowler-Nordheim simples de CFE a partir de metales se obtiene poniendo λ Z →1, P F → 1, → v ( f ). Esto regenera la ecuación de tipo Fowler-Nordheim utilizada por Dyke y Dolan en 1956, y puede llamarse la "ecuación de tipo Fowler-Nordheim estándar simplificada".
Explícitamente, esta ecuación estándar simplificada recomendada de tipo Fowler-Nordheim y las fórmulas asociadas son:
donde F φ aquí es el campo necesario para reducir a cero una barrera Schottky–Nordheim de altura no reducida igual a la función de trabajo local φ , y f es el campo de barrera escalado para una barrera Schottky–Nordheim de altura no reducida φ . [Esta cantidad f podría haberse escrito más exactamente como f φ SN , pero hace que esta ecuación de tipo Fowler–Nordheim parezca menos desordenada si se adopta la convención de que f simple significa la cantidad denotada por f φ SN en, [69] ecuación (2.16).] Para el caso de ejemplo ( φ = 4,5 eV, F = 5 V/nm), f ≈ 0,36 y v ( f ) ≈ 0,58; los rangos prácticos para estos parámetros se discuten más adelante en. [77]
Obsérvese que la variable f (el campo de barrera escalado) no es la misma que la variable y (el parámetro de Nordheim) ampliamente utilizada en la literatura de emisión de campo anterior, y que " v ( f ) " NO tiene el mismo significado matemático y valores que la cantidad " v ( y ) " que aparece en la literatura de emisión de campo. En el contexto de la teoría revisada descrita aquí, las fórmulas para v ( y ), y las tablas de valores para v ( y ) deben ignorarse, o tratarse como valores de v ( f 1/2 ). Si se requieren valores más exactos para v ( f ), entonces [69] proporciona fórmulas que dan valores para v ( f ) con una precisión matemática absoluta mejor que 8×10 −10 . Sin embargo, la fórmula de aproximación (30c) anterior, que produce valores correctos dentro de una precisión matemática absoluta mejor que 0,0025, debería dar valores suficientemente precisos para todos los fines tecnológicos. [69]
Es necesaria una nota histórica sobre los métodos de derivación de ecuaciones de tipo Fowler-Nordheim. Hay varios enfoques posibles para derivar estas ecuaciones, utilizando la teoría de electrones libres . El enfoque utilizado aquí fue introducido por Forbes en 2004 y puede describirse como "integración a través de la distribución total de energía, utilizando la energía cinética paralela K p como la primera variable de integración". [73] Básicamente, es un equivalente de electrones libres del procedimiento de Modinos [33] [75] (en un tratamiento mecánico cuántico más avanzado) de "integración sobre la zona de Brillouin de la superficie". Por el contrario, los tratamientos de electrones libres de CFE de Young en 1959, [31] Gadzuk y Plummer en 1973 [34] y Modinos en 1984, [33] también integran a través de la distribución total de energía, pero utilizan la energía normal ε n (o una cantidad relacionada) como la primera variable de integración.
También existe un enfoque más antiguo, basado en un artículo seminal de Nordheim en 1928, [78] que formula el problema de manera diferente y luego usa primero K p y luego ε n (o una cantidad relacionada) como las variables de integración: esto se conoce como "integración a través de la distribución de energía normal". Este enfoque continúa siendo utilizado por algunos autores. Aunque tiene algunas ventajas, particularmente cuando se analizan los fenómenos de resonancia, requiere la integración de la función de distribución de Fermi-Dirac en la primera etapa de la integración: para estructuras de bandas electrónicas no similares a las de los electrones libres, esto puede conducir a matemáticas muy complejas y propensas a errores (como en el trabajo de Stratton sobre semiconductores ). [79] Además, la integración a través de la distribución de energía normal no genera distribuciones de energía de electrones medidas experimentalmente.
En general, el enfoque utilizado aquí parece más fácil de entender y conduce a matemáticas más simples.
También está más cerca en principio de los enfoques más sofisticados utilizados cuando se trata con sólidos cristalinos reales en masa, donde el primer paso es integrar las contribuciones a la ECD sobre superficies de energía constante en un espacio de vector de onda ( espacio k ), [34] o integrar las contribuciones sobre la zona de Brillouin de la superficie relevante. [33] El enfoque de Forbes es equivalente a integrar sobre una superficie esférica en el espacio k , utilizando la variable K p para definir un elemento de integración tipo anillo que tiene simetría cilíndrica sobre un eje en una dirección normal a la superficie emisora, o a integrar sobre una zona de Brillouin de superficie (extendida) utilizando elementos de anillo circular.
En la sección anterior se explica cómo derivar ecuaciones de tipo Fowler-Nordheim. Estrictamente, estas ecuaciones se aplican únicamente a la CFE a partir de metales a granel. Las ideas de las secciones siguientes se aplican a la CFE de manera más general, pero se utilizará la ecuación (30) para ilustrarlas.
Para la CFE, los tratamientos teóricos básicos proporcionan una relación entre la densidad de corriente de emisión local J y el campo de barrera local F , en una posición local en la superficie de emisión. Los experimentos miden la corriente de emisión i desde alguna parte definida de la superficie de emisión, como una función del voltaje V aplicado a algún contraelectrodo. Para relacionar estas variables con J y F , se utilizan ecuaciones auxiliares.
El factor de conversión de voltaje a campo de barrera β se define por:
El valor de F varía de una posición a otra en la superficie de un emisor, y el valor de β varía correspondientemente.
Para un emisor metálico, el valor β− para una posición dada será constante (independiente del voltaje) bajo las siguientes condiciones: (1) el aparato es una disposición de "diodos", donde los únicos electrodos presentes son el emisor y un conjunto de "alrededores", todas partes de las cuales están al mismo voltaje; (2) no hay carga espacial de vacío emitida por campo (FEVSC) significativa (esto será cierto excepto a densidades de corriente de emisión muy altas, alrededor de 10 9 A/m 2 o más [27] [80] ); (3) no existen "campos de parches" significativos, [63] como resultado de no uniformidades en la función de trabajo local (normalmente se asume que esto es cierto, pero puede no serlo en algunas circunstancias). Para los no metales, los efectos físicos llamados "penetración de campo" y " flexión de banda " [M084] pueden hacer que β sea una función del voltaje aplicado, aunque -sorprendentemente- hay pocos estudios de este efecto.
La densidad de corriente de emisión J varía de una posición a otra a lo largo de la superficie del emisor. La corriente de emisión total i de una parte definida del emisor se obtiene integrando J a lo largo de esta parte. Para obtener una ecuación simple para i ( V ), se utiliza el siguiente procedimiento. Se selecciona un punto de referencia "r" dentro de esta parte de la superficie del emisor (a menudo el punto en el que la densidad de corriente es más alta), y la densidad de corriente en este punto de referencia se denota por J r . Un parámetro A r , llamado área de emisión nocional (con respecto al punto "r"), se define entonces por:
donde la integral se toma a través de la parte del emisor de interés.
Este parámetro A r fue introducido en la teoría de CFE por Stern, Gossling y Fowler en 1929 (quienes lo llamaron un "área media ponderada"). [16] Para emisores prácticos, la densidad de corriente de emisión utilizada en ecuaciones de tipo Fowler-Nordheim es siempre la densidad de corriente en algún punto de referencia (aunque esto no suele indicarse). La convención establecida desde hace mucho tiempo denota esta densidad de corriente de referencia mediante el símbolo simple J , y el campo local correspondiente y el factor de conversión mediante los símbolos simples F y β , sin el subíndice "r" utilizado anteriormente; en lo que sigue, se utiliza esta convención.
El área de emisión nocional A r a menudo será una función del campo local de referencia (y, por lo tanto, del voltaje), [30] y en algunas circunstancias podría ser una función significativa de la temperatura.
Debido a que A r tiene una definición matemática, no necesariamente corresponde al área desde la cual se observa que se produce la emisión desde un emisor de un solo punto en un microscopio electrónico de campo (de emisión) . Con un emisor de área grande, que contiene muchos sitios de emisión individuales, A r casi siempre será muy, muy [ aclaración necesaria ] mucho menor que el área geométrica "macroscópica" ( AM ) del emisor como se observa visualmente (ver a continuación) .
Incorporando estas ecuaciones auxiliares en la ecuación (30a) se obtiene
Esta es la ecuación estándar simplificada de tipo Fowler-Nordheim, en forma i - V. La ecuación "físicamente completa" correspondiente se obtiene multiplicando por λ Z P F .
Las ecuaciones de la sección anterior se aplican a todos los emisores de campo que operan en el régimen de CFE. Sin embargo, desarrollos posteriores son útiles para emisores de área extensa que contienen muchos sitios de emisión individuales.
Para tales emisores, el área de emisión nocional será casi siempre muy [ aclaración necesaria ] mucho menor que el área geométrica "macroscópica" aparente ( A M ) del emisor físico tal como se observa visualmente. Un parámetro adimensional α r , la eficiencia del área de emisión , se puede definir por
Además, se puede definir una densidad de corriente de emisión "macroscópica" (o "media") J M (promediada sobre el área geométrica A M del emisor), y relacionarla con la densidad de corriente de referencia J r utilizada anteriormente, mediante
Esto conduce a las siguientes "versiones de área grande" de la ecuación estándar simplificada de tipo Fowler-Nordheim:
Ambas ecuaciones contienen la eficiencia de área de emisión α r . Para cualquier emisor dado, este parámetro tiene un valor que normalmente no se conoce bien. En general, α r varía mucho entre diferentes materiales de emisor y entre diferentes muestras del mismo material preparadas y procesadas de diferentes maneras. Parece probable que se encuentren valores en el rango de 10 −10 a 10 −6 , y pueden ser posibles valores fuera de este rango.
La presencia de α r en la ecuación (36) explica la diferencia entre las densidades de corriente macroscópicas que a menudo se citan en la literatura (normalmente 10 A/m 2 para muchas formas de emisores de área grande distintos de los conjuntos Spindt [50] ) y las densidades de corriente locales en los sitios de emisión reales, que pueden variar ampliamente pero que se cree que son generalmente del orden de 10 9 A/m 2 , o posiblemente ligeramente menos.
Una parte importante de la literatura tecnológica sobre emisores de gran superficie no establece distinciones claras entre densidades de corriente locales y macroscópicas, o entre el área de emisión teórica Ar y el área macroscópica AM , y / o omite el parámetro αr de las ecuaciones citadas. Es necesario tener cuidado para evitar errores de interpretación.
A veces también es conveniente dividir el factor de conversión β r en una "parte macroscópica" que se relaciona con la geometría general del emisor y sus alrededores, y una "parte local" que se relaciona con la capacidad de la estructura muy local de la superficie del emisor para mejorar el campo eléctrico. Esto se hace generalmente definiendo un "campo macroscópico" F M que es el campo que estaría presente en el sitio de emisión en ausencia de la estructura local que causa la mejora. Este campo F M está relacionado con el voltaje aplicado por un "factor de conversión de voltaje a campo macroscópico" β M definido por:
En el caso común de un sistema que comprende dos placas paralelas, separadas por una distancia W , con nanoestructuras emisoras creadas en una de ellas, β M = 1/ W .
Luego se define un "factor de mejora de campo" γ y se relaciona con los valores de β r y β M mediante
Con la ecuación (31), se generan las siguientes fórmulas:
donde, de acuerdo con la convención habitual, el sufijo "r" se ha eliminado de los parámetros relacionados con el punto de referencia. Existen fórmulas para la estimación de γ , utilizando la electrostática clásica , para una variedad de formas de emisor, en particular el "hemisferio sobre un poste". [81]
La ecuación (40) implica que se pueden escribir versiones de ecuaciones de tipo Fowler-Nordheim donde F o βV se reemplazan en todas partes por . Esto se hace a menudo en aplicaciones tecnológicas donde el interés principal está en las propiedades de mejora del campo de la nanoestructura del emisor local. Sin embargo, en algunos trabajos anteriores, la falta de una distinción clara entre el campo de barrera F y el campo macroscópico F M ha causado confusión o error.
En términos más generales, los objetivos del desarrollo tecnológico de emisores de campo de gran área son mejorar la uniformidad de la emisión incrementando el valor de la eficiencia de área de emisión α r , y reducir el voltaje de "inicio" en el que se produce una emisión significativa, incrementando el valor de β . La ecuación (41) muestra que esto se puede hacer de dos maneras: ya sea tratando de desarrollar nanoestructuras de "alto γ ", o modificando la geometría general del sistema de modo que β M aumente. Existen varias compensaciones y restricciones.
En la práctica, aunque la definición de campo macroscópico utilizada anteriormente es la más común, en la literatura se utilizan otros tipos de campo macroscópico y factor de mejora de campo (definidos de manera diferente), particularmente en relación con el uso de sondas para investigar las características i - V de emisores individuales. [82]
En contextos tecnológicos, los datos de emisión de campo se suelen representar gráficamente utilizando (una definición particular de) F M o 1/ F M como la coordenada x . Sin embargo, para el análisis científico suele ser mejor no manipular previamente los datos experimentales, sino representar gráficamente directamente los datos i - V medidos en bruto . Los valores de los parámetros tecnológicos como (las diversas formas de) γ se pueden obtener a partir de los parámetros ajustados del gráfico de datos i - V (véase más abajo), utilizando las definiciones pertinentes.
La mayoría de las derivaciones teóricas en la teoría de emisión de campo se realizan bajo el supuesto de que la barrera adopta la forma Schottky-Nordheim ecuación (3). Sin embargo, esta forma de barrera no es válida para emisores con radios de curvatura comparables a la longitud de la barrera de efecto túnel. Esto último depende de la función de trabajo y del campo, pero en casos de interés práctico, la aproximación de barrera SN puede considerarse válida para emisores con radios , como se explica en el siguiente párrafo.
El supuesto principal de la aproximación de barrera SN es que el término de potencial electrostático toma la forma lineal en la región de tunelización. Se ha demostrado que esto último se cumple solo si . [83] Por lo tanto, si la región de tunelización tiene una longitud , para todo lo que determina el proceso de tunelización; por lo tanto, si la ecuación (1) se cumple y la aproximación de barrera SN es válida. Si la probabilidad de tunelización es lo suficientemente alta como para producir una emisión de campo medible, L no excede de 1-2 nm. Por lo tanto, la barrera SN es válida para emisores con radios del orden de algunas decenas de nm.
Sin embargo, los emisores modernos son mucho más agudos que esto, con radios del orden de unos pocos nm. Por lo tanto, la ecuación FN estándar, o cualquier versión de la misma que suponga la barrera SN, conduce a errores significativos para emisores tan agudos. Esto se ha demostrado tanto teóricamente [84] [85] como confirmado experimentalmente. [86]
El problema anterior fue abordado por Kyritsakis y Xanthakis [83] , quienes generalizaron la barrera SN al incluir los efectos electrostáticos de la curvatura del emisor. La forma general de la barrera para un emisor con un radio de curvatura promedio (inverso del promedio de las dos curvaturas principales) se puede expandir asintóticamente como [87]
Después de descuidar todos los términos y emplear la aproximación JWKB (4) para esta barrera, el exponente de Gamow toma una forma que generaliza la ecuación (5).
donde se define por (30d), se da por (30c) y es una nueva función que se puede aproximar de manera similar a (30c) (hay errores tipográficos en la referencia, [83] corregido aquí):
Dada la expresión para el exponente de Gamow como función de la altura de barrera libre de campo , la densidad de corriente emitida para la emisión de campo frío se puede obtener de la ecuación (23). Se obtiene
donde las funciones y se definen como
y
En la ecuación (46), por razones de exhaustividad, no se aproxima por la unidad como en (29) y (30a), aunque para la mayoría de los casos prácticos es una aproximación muy buena. Aparte de esto, las ecuaciones (43), (44) y (46) coinciden con las correspondientes de la teoría estándar de Fowler-Nordheim (3), (9) y (30a), en el límite ; esto es esperable ya que las primeras ecuaciones generalizan las segundas.
Por último, tenga en cuenta que el análisis anterior es asintótico en el límite , de manera similar a la teoría estándar de Fowler-Nordheim que utiliza la barrera SN. Sin embargo, la adición de los términos cuadráticos lo hace significativamente más preciso para emisores con radios de curvatura en el rango de ~5–20 nm. Para emisores más agudos, no existe una aproximación general para la densidad de corriente. Para obtener la densidad de corriente, uno tiene que calcular el potencial electrostático y evaluar numéricamente la integral JWKB . Para este propósito, se ha desarrollado un software de computación científica (ver, por ejemplo, GETELEC [88] ).
En la etapa actual del desarrollo de la teoría de la CFE, es importante hacer una distinción entre ecuaciones de CFE teóricas y ecuaciones de CFE empíricas. Las primeras se derivan de la física de la materia condensada (si bien en contextos donde su desarrollo detallado es difícil). Una ecuación de CFE empírica, por otro lado, simplemente intenta representar la forma experimental real de la dependencia de la corriente i con respecto al voltaje V .
En la década de 1920, se utilizaron ecuaciones empíricas para encontrar la potencia de V que aparecía en el exponente de una ecuación semilogarítmica que se suponía que describía los resultados experimentales de la CFE. En 1928, se unieron la teoría y la experimentación para demostrar que (excepto, posiblemente, para emisores muy agudos) esta potencia es V −1 . Recientemente se ha sugerido que ahora se deberían realizar experimentos de CFE para intentar encontrar la potencia ( κ ) de V en el preexponencial de la siguiente ecuación empírica de CFE: [89]
donde B , C y κ se tratan como constantes.
De la ecuación (42) se demuestra fácilmente que
En la década de 1920, las técnicas experimentales no podían distinguir entre los resultados κ = 0 (asumido por Millikan y Laurtisen) [13] y κ = 2 (predicho por la ecuación original de tipo Fowler-Nordheim). [1] Sin embargo, ahora debería ser posible hacer mediciones razonablemente precisas de dlni/d(1/V) (si es necesario, utilizando técnicas de detección de fase sensible/ amplificador de bloqueo y equipo controlado por computadora), y derivar κ de la pendiente de un gráfico de datos apropiado. [50]
Tras el descubrimiento de la aproximación (30b), ahora está muy claro que, incluso para la CFE a partir de metales a granel, no se espera el valor κ = 2. Esto se puede demostrar de la siguiente manera. Utilizando la ecuación (30c) anterior, un parámetro adimensional η se puede definir mediante
Para φ = 4,50 eV, este parámetro tiene el valor η = 4,64. Dado que f = F / F φ y v ( f ) se da por la ecuación (30b), el exponente en la ecuación estándar simplificada de tipo Fowler-Nordheim (30) se puede escribir en una forma alternativa y luego expandir de la siguiente manera: [69]
Suponiendo que el factor de conversión β es independiente del voltaje, el parámetro f tiene la definición alternativa f = V / V φ , donde V φ es el voltaje necesario, en un sistema experimental particular, para reducir la altura de una barrera Schottky–Nordheim de φ a cero. Por lo tanto, es claro que el factor v ( f ) en el exponente de la ecuación teórica (30) da lugar a una dependencia adicional de V en el preexponencial de la ecuación empírica. Por lo tanto, (para efectos debidos a la barrera Schottky–Nordheim, y para un emisor con φ =4,5 eV) obtenemos la predicción:
Dado que también puede haber dependencia de voltaje en otros factores en una ecuación de tipo Fowler-Nordheim, en particular en el área de emisión nocional [30] A r y en la función de trabajo local, no se espera necesariamente que κ para CFE de un metal de función de trabajo local 4,5 eV tenga el valor κ = 1,23, pero ciertamente no hay razón para esperar que tenga el valor original de Fowler-Nordheim κ = 2. [90]
Kirk realizó una primera prueba experimental de esta propuesta, utilizando una forma ligeramente más compleja de análisis de datos para hallar un valor de 1,36 para su parámetro κ . Su parámetro κ es muy similar, pero no exactamente igual, al parámetro κ utilizado aquí, pero no obstante sus resultados parecen confirmar la utilidad potencial de esta forma de análisis. [91]
El uso de la ecuación empírica de CFE (42) y la medición de κ pueden ser de particular utilidad para los no metales. Estrictamente, las ecuaciones de tipo Fowler-Nordheim se aplican solo a la emisión desde la banda de conducción de sólidos cristalinos en masa . Sin embargo, las ecuaciones empíricas de la forma (42) deberían aplicarse a todos los materiales (aunque, posiblemente, podría ser necesaria una modificación para emisores muy agudos). Parece muy probable que una forma en que las ecuaciones de CFE para materiales más nuevos pueden diferir de las ecuaciones de tipo Fowler-Nordheim es que estas ecuaciones de CFE pueden tener una potencia diferente de F (o V ) en sus preexponenciales. Las mediciones de κ podrían proporcionar alguna indicación experimental de esto.
La ecuación teórica original derivada por Fowler y Nordheim [1] ha influido, durante los últimos 80 años, en la forma en que se han graficado y analizado los datos experimentales de CFE. En el gráfico de Fowler-Nordheim, ampliamente utilizado, introducido por Stern et al. en 1929, [16] la cantidad ln{ i / V 2 } se grafica frente a 1/ V . La idea original era que (como predecía la ecuación original o la elemental de tipo Fowler-Nordheim) esto generaría una línea recta exacta de pendiente S FN . S FN estaría relacionada con los parámetros que aparecen en el exponente de una ecuación de tipo Fowler-Nordheim de la forma i - V por:
Por lo tanto, el conocimiento de φ permitiría determinar β , o viceversa.
[En principio, en geometrías de sistemas donde hay una nanoestructura que mejora el campo local y se puede determinar el factor de conversión macroscópico β M , el conocimiento de β permite determinar el valor del factor de mejora del campo efectivo del emisor γ a partir de la fórmula γ = β / β M . En el caso común de un emisor de película generado en una placa de una disposición de dos placas con separación de placas W (por lo que β M = 1/ W ), entonces
Hoy en día, esta es una de las aplicaciones más probables de los gráficos de Fowler-Nordheim.]
Posteriormente se hizo evidente que el razonamiento original anterior es estrictamente correcto sólo para la situación físicamente irreal de un emisor plano y una barrera triangular exacta. Para los emisores y barreras reales se debe introducir un "factor de corrección de pendiente" σFN, lo que da como resultado la fórmula revisada
El valor de σFN , en principio, estará influenciado por cualquier parámetro en la ecuación de tipo Fowler-Nordheim físicamente completa para i ( V ) que tenga una dependencia del voltaje.
En la actualidad, el único parámetro que se considera importante es el factor de corrección relacionado con la forma de la barrera, y la única barrera para la que existe una teoría detallada bien establecida es la barrera Schottky-Nordheim. En este caso, σ FN viene dada por una función matemática llamada s . Esta función s fue tabulada correctamente por primera vez (como una función del parámetro Nordheim y ) por Burgess, Kroemer y Houston en 1953; [71] y un tratamiento moderno que da s como función del campo de barrera escalado f para una barrera Schottky-Nordheim se da en. [69] Sin embargo, desde hace tiempo está claro que, para el funcionamiento práctico del emisor, el valor de s se encuentra en el rango de 0,9 a 1.
En la práctica, debido a la complejidad adicional que implica tener en cuenta en detalle el factor de corrección de pendiente, muchos autores (en efecto) ponen σFN = 1 en la ecuación (49), generando así un error sistemático en sus valores estimados de β y/o γ , que generalmente se considera que ronda el 5%.
Sin embargo, la ecuación empírica (42), que en principio es más general que las ecuaciones de tipo Fowler-Nordheim, trae consigo posibles nuevas formas de analizar los datos de emisión de campo i - V. En general, se puede suponer que el parámetro B en la ecuación empírica está relacionado con la altura no reducida H de alguna barrera característica vista por los electrones tunelizadores mediante
(En la mayoría de los casos, pero no necesariamente en todos, H sería igual a la función de trabajo local; ciertamente esto es cierto para los metales.) La cuestión es cómo determinar el valor de B mediante experimentos. Hay dos formas obvias. (1) Supongamos que la ecuación (43) se puede utilizar para determinar un valor experimental razonablemente preciso de κ , a partir de la pendiente de un gráfico de la forma [−dln{ i }/d(1/ V ) vs. V ]. En este caso, un segundo gráfico, de ln( i )/ V κ vs. 1/ V , debería ser una línea recta exacta de pendiente − B . Este enfoque debería ser la forma más precisa de determinar B .
(2) Alternativamente, si el valor de κ no se conoce con exactitud y no se puede medir con precisión, pero se puede estimar o adivinar, entonces se puede derivar un valor para B a partir de un gráfico de la forma [ln{ i } vs. 1/ V ]. Esta es la forma de gráfico utilizada por Millikan y Lauritsen en 1928. Reordenando la ecuación (43) se obtiene
Por lo tanto, B se puede determinar, con un buen grado de aproximación, determinando la pendiente media de un gráfico de Millikan-Lauritsen en un rango de valores de 1/ V y aplicando una corrección, utilizando el valor de 1/ V en el punto medio del rango y un valor supuesto de κ .
Las principales ventajas de utilizar un gráfico de Millikan-Lauritsen y esta forma de procedimiento de corrección, en lugar de un gráfico de Fowler-Nordheim y un factor de corrección de pendiente, son las siguientes. (1) El procedimiento de trazado es marginalmente más sencillo. (2) La corrección implica un parámetro físico ( V ) que es una cantidad medida, en lugar de un parámetro físico ( f ) que tiene que calcularse [para luego calcular un valor de s ( f ) o, más generalmente σ FN ( f )]. (3) Tanto el parámetro κ en sí mismo como el procedimiento de corrección son más transparentes (y más fáciles de entender) que los equivalentes del gráfico de Fowler-Nordheim. (4) Este procedimiento tiene en cuenta todos los efectos físicos que influyen en el valor de κ , mientras que el procedimiento de corrección del diagrama de Fowler-Nordheim (en la forma en que se ha llevado a cabo durante los últimos 50 años) tiene en cuenta sólo aquellos efectos asociados con la forma de la barrera, suponiendo, además, que esta forma es la de una barrera de Schottky-Nordheim. (5) Hay una separación más clara de las preocupaciones teóricas y tecnológicas: los teóricos estarán interesados en establecer qué información proporcionan los valores medidos de κ sobre la teoría de la CFE; pero los experimentalistas pueden simplemente usar los valores medidos de κ para hacer estimaciones más precisas (si es necesario) de los factores de mejora del campo. [ cita requerida ]
Este procedimiento de corrección para los diagramas de Millikan-Lauritsen será más fácil de aplicar cuando se haya realizado una cantidad suficiente de mediciones de κ y se tenga una mejor idea de cuáles son realmente los valores típicos. En la actualidad, parece probable que para la mayoría de los materiales κ se encuentre en el rango -1< κ <3. [ cita requerida ]
Desarrollar la teoría aproximada de CFE a partir de los metales anteriores es comparativamente fácil, por las siguientes razones. (1) La teoría de electrones libres de Sommerfeld, con sus suposiciones particulares sobre la distribución de estados electrónicos internos en energía, se aplica adecuadamente a muchos metales como una primera aproximación. (2) La mayoría de las veces, los metales no tienen estados superficiales y (en muchos casos) las funciones de onda de los metales no tienen " resonancias superficiales " significativas. (3) Los metales tienen una alta densidad de estados en el nivel de Fermi, por lo que la carga que genera/protege los campos eléctricos externos se encuentra principalmente en el exterior de la capa atómica superior, y no ocurre una "penetración de campo" significativa. (4) Los metales tienen alta conductividad eléctrica : no ocurren caídas de voltaje significativas dentro de los emisores metálicos: esto significa que no hay factores que obstruyan el suministro de electrones a la superficie emisora, y que los electrones en esta región pueden estar tanto en equilibrio termodinámico local efectivo como en equilibrio termodinámico efectivo con los electrones en la estructura de soporte metálica en la que está montado el emisor. (5) No se tienen en cuenta los efectos a nivel atómico. [ cita requerida ]
El desarrollo de teorías "simples" de emisión de electrones de campo, y en particular el desarrollo de ecuaciones de tipo Fowler-Nordheim, se basa en que los cinco factores anteriores sean verdaderos. Para materiales distintos de los metales (y para emisores metálicos atómicamente agudos) uno o más de los factores anteriores serán falsos. Por ejemplo, los semiconductores cristalinos no tienen una estructura de bandas similar a la de los electrones libres, tienen estados superficiales, están sujetos a la penetración de campo y a la flexión de bandas , y pueden presentar tanto caídas de voltaje internas como desacoplamiento estadístico de la distribución de electrones del estado superficial de la distribución de electrones en la región superficial de la estructura de bandas en masa (este desacoplamiento se conoce como "el efecto Modinos"). [33] [92]
En la práctica, la teoría del proceso de tunelación de Fowler-Nordheim es muy similar para todos los materiales (aunque los detalles de la forma de la barrera pueden variar y se debe desarrollar una teoría modificada para estados iniciales que sean localizados en lugar de ondas viajeras ). Sin embargo, a pesar de estas diferencias, se espera (para situaciones de equilibrio termodinámico) que todas las ecuaciones de CFE tengan exponentes que se comporten de una manera generalmente similar. Esta es la razón por la que la aplicación de ecuaciones de tipo Fowler-Nordheim a materiales fuera del alcance de las derivaciones dadas aquí a menudo funciona. Si el interés está solo en los parámetros (como el factor de mejora de campo) que se relacionan con la pendiente de los gráficos de Fowler-Nordheim o Millikan-Lauritsen y con el exponente de la ecuación de CFE, entonces la teoría de tipo Fowler-Nordheim a menudo dará estimaciones sensatas. Sin embargo, los intentos de derivar valores de densidad de corriente significativos generalmente o siempre fallarán.
Obsérvese que una línea recta en un diagrama de Fowler-Nordheim o Millikan-Lauritsen no indica que la emisión del material correspondiente obedezca a una ecuación de tipo Fowler-Nordheim: sólo indica que el mecanismo de emisión de los electrones individuales es probablemente el efecto túnel de Fowler-Nordheim. [ cita requerida ]
Diferentes materiales pueden tener distribuciones radicalmente diferentes de la energía de sus estados electrónicos internos, por lo que el proceso de integración de las contribuciones de la densidad de corriente sobre los estados electrónicos internos puede dar lugar a expresiones significativamente diferentes para los preexponenciales de densidad de corriente, para diferentes clases de materiales. En particular, la potencia del campo de barrera que aparece en el preexponencial puede ser diferente del valor original de Fowler-Nordheim "2". La investigación de efectos de este tipo es un tema de investigación activo. Los efectos de "resonancia" y " dispersión " a nivel atómico, si ocurren, también modificarán la teoría.
Cuando los materiales están sujetos a la penetración de campos y a la flexión de bandas, es necesario contar con buenas teorías de dichos efectos (para cada clase diferente de material) antes de poder desarrollar teorías detalladas de la corriente de emisión. Cuando se producen efectos de caída de tensión, la teoría de la corriente de emisión puede, en mayor o menor medida, convertirse en una teoría que involucre efectos de transporte interno y puede llegar a ser muy compleja.
{{cite journal}}: Falta o está vacío |title=( ayuda ){{cite journal}}: Requiere citar revista |journal=( ayuda ){{cite journal}}: Falta o está vacío |title=( ayuda )Penetración de campo y flexión de banda (semiconductores)