En física atómica , un número cuántico magnético es un número cuántico utilizado para distinguir estados cuánticos de un electrón u otra partícula según su momento angular a lo largo de un eje dado en el espacio. El número cuántico magnético orbital ( m l o m [a] ) distingue los orbitales disponibles dentro de una subcapa dada de un átomo. Especifica el componente del momento angular orbital que se encuentra a lo largo de un eje dado, convencionalmente llamado eje z , por lo que describe la orientación del orbital en el espacio. El número cuántico magnético de espín m s especifica el componente del eje z del momento angular de espín para una partícula que tiene un número cuántico de espín s . Para un electrón, s es 1 ⁄ 2 , y m s es + 1 ⁄ 2 o − 1 ⁄ 2 , a menudo llamado "spin-up" y "spin-down", o α y β. [1] [2] El término magnético en el nombre se refiere al momento dipolar magnético asociado con cada tipo de momento angular, por lo que los estados que tienen diferentes números cuánticos magnéticos cambian de energía en un campo magnético de acuerdo con el efecto Zeeman . [2]
Los cuatro números cuánticos que se usan convencionalmente para describir el estado cuántico de un electrón en un átomo son el número cuántico principal n , el número cuántico azimutal (orbital) y los números cuánticos magnéticos m l y m s . Los electrones en una subcapa dada de un átomo (como s, p, d o f) se definen por valores de (0, 1, 2 o 3). El número cuántico magnético orbital toma valores enteros en el rango de a , incluido cero. [3] Por lo tanto, las subcapas s, p, d y f contienen 1, 3, 5 y 7 orbitales cada una. Cada uno de estos orbitales puede acomodar hasta dos electrones (con espines opuestos), formando la base de la tabla periódica .
Otros números cuánticos magnéticos se definen de manera similar, como m j para el componente del eje z , el momento angular electrónico total j , [1] y m I para el espín nuclear I . [2] Los números cuánticos magnéticos se escriben con mayúscula para indicar los totales de un sistema de partículas, como M L o m L para el momento angular orbital total del eje z de todos los electrones en un átomo. [2]
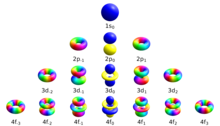
Existe un conjunto de números cuánticos asociados con los estados de energía del átomo. Los cuatro números cuánticos , , , y especifican el estado cuántico completo de un solo electrón en un átomo llamado su función de onda u orbital . La ecuación de Schrödinger para la función de onda de un átomo con un electrón es una ecuación diferencial parcial separable . (Este no es el caso del átomo de helio neutro u otros átomos con electrones que interactúan mutuamente, que requieren métodos más sofisticados para su solución [4] ) Esto significa que la función de onda expresada en coordenadas esféricas se puede descomponer en el producto de tres funciones del radio, el ángulo de colatitud (o polar) y el acimut: [5]
La ecuación diferencial para se puede resolver en la forma . Debido a que los valores del ángulo acimutal que difieren en 2 radianes (360 grados) representan la misma posición en el espacio, y la magnitud total de no crece con arbitrariamente grande como lo haría para un exponente real, el coeficiente debe cuantificarse a múltiplos enteros de , produciendo un exponente imaginario : . [6] Estos números enteros son los números cuánticos magnéticos. La misma constante aparece en la ecuación de colatitud, donde los valores más grandes de tienden a disminuir la magnitud de y los valores de mayores que el número cuántico acimutal no permiten ninguna solución para

El eje utilizado para las coordenadas polares en este análisis se elige arbitrariamente. El número cuántico se refiere a la proyección del momento angular en esta dirección elegida arbitrariamente, llamada convencionalmente dirección o eje de cuantificación. , la magnitud del momento angular en la dirección , se da mediante la fórmula: [7]
Este es un componente del momento angular orbital total del electrón atómico , cuya magnitud está relacionada con el número cuántico azimutal de su subcapa por la ecuación:
donde es la constante de Planck reducida . Nótese que esto para y se aproxima para alta . No es posible medir el momento angular del electrón a lo largo de los tres ejes simultáneamente. Estas propiedades fueron demostradas por primera vez en el experimento de Stern-Gerlach , por Otto Stern y Walther Gerlach . [8]
El número cuántico se refiere, en términos generales, a la dirección del vector del momento angular . El número cuántico magnético solo afecta a la energía del electrón si se encuentra en un campo magnético porque, en ausencia de uno, todos los armónicos esféricos correspondientes a los diferentes valores arbitrarios de son equivalentes. El número cuántico magnético determina el desplazamiento de energía de un orbital atómico debido a un campo magnético externo (el efecto Zeeman ), de ahí el nombre de número cuántico magnético . Sin embargo, el momento dipolar magnético real de un electrón en un orbital atómico surge no solo del momento angular del electrón, sino también del espín del electrón, expresado en el número cuántico de espín .
Como cada electrón tiene un momento magnético en un campo magnético, estará sujeto a un torque que tiende a hacer que el vector sea paralelo al campo, un fenómeno conocido como precesión de Larmor .