En el centro

Centro de la circunferencia inscrita de un triángulo

El punto de intersección de las bisectrices de los 3 ángulos del triángulo ABC es el incentro (denotado por I). El círculo (cuyo centro es I) toca cada lado del triángulo.

En geometría , el incentro de un triángulo es el centro del triángulo , un punto definido para cualquier triángulo de una manera independiente de la ubicación o escala del triángulo. El incentro puede definirse de manera equivalente como el punto donde se cruzan las bisectrices del ángulo interno del triángulo, como el punto equidistante de los lados del triángulo, como el punto de unión del eje medial y el punto más interno de la transformada de hierba del triángulo, y como el Punto central de la circunferencia inscrita del triángulo.

Junto con el centroide , el circuncentro y el ortocentro , es uno de los cuatro centros de triángulos conocidos por los antiguos griegos, y el único de los cuatro que, en general, no se encuentra en la recta de Euler . Es el primer centro listado, X(1), en la Enciclopedia de centros de triángulos de Clark Kimberling , y el elemento de identidad del grupo multiplicativo de centros de triángulos. ^{[1] [2]}

Para polígonos con más de tres lados, el incentro solo existe para polígonos tangenciales , aquellos que tienen un círculo que es tangente a cada lado del polígono. En este caso el incentro es el centro de este círculo y está a la misma distancia de todos los lados.

Definición y construcción

Es un teorema de la geometría euclidiana que las tres bisectrices de un ángulo interior de un triángulo se encuentran en un solo punto. En los Elementos de Euclides , la Proposición 4 del Libro IV demuestra que este punto es también el centro de la circunferencia inscrita del triángulo. El círculo en sí se puede construir trazando una perpendicular desde el incentro a uno de los lados del triángulo y dibujando un círculo con ese segmento como radio. ^[3]

El incentro se encuentra a distancias iguales de los tres segmentos que forman los lados del triángulo, y también de las tres rectas que contienen esos segmentos. Es el único punto igualmente distante de los segmentos de recta, pero hay tres puntos más igualmente distantes de las rectas, los excentros, que forman los centros de los excírculos del triángulo dado. El incentro y los excentros juntos forman un sistema ortocéntrico . ^[4]

El eje medial de un polígono es el conjunto de puntos cuyo vecino más cercano en el polígono no es único: estos puntos son equidistantes de dos o más lados del polígono. Un método para calcular los ejes mediales es utilizar la transformada Grassfire , en la que se forma una secuencia continua de curvas desplazadas , cada una a una distancia fija del polígono; el eje medial está trazado por los vértices de estas curvas. En el caso de un triángulo, el eje medial consta de tres segmentos de las bisectrices del ángulo, que conectan los vértices del triángulo con el incentro, que es el único punto en la curva de desplazamiento más interna. ^[5] El esqueleto recto , definido de manera similar a partir de un tipo diferente de curva desplazada, coincide con el eje medial para polígonos convexos y por lo tanto también tiene su unión en el incentro. ^[6]

Pruebas

prueba de relación

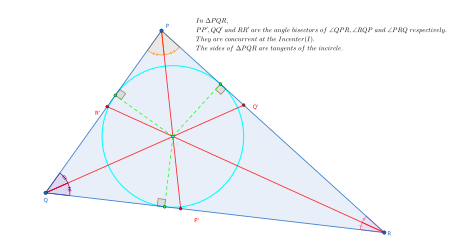
Sea la bisección de y encontrarse en , y la bisección de y encontrarse en , y y encontrarse en . ${\displaystyle \angle {BAC}}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle D}$ ${\displaystyle \angle {ABC}}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle E}$ ${\displaystyle {\overline {AD}}}$ ${\displaystyle {\overline {BE}}}$ ${\displaystyle {I}}$

Y deja que nos reunamos en . ${\displaystyle {\overline {CI}}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle {F}}$

Entonces tenemos que demostrar que es la bisección de . ${\displaystyle {\overline {CI}}}$ ${\displaystyle \angle {ACB}}$

En , , por el teorema de la bisectriz del ángulo . ${\displaystyle \triangle {ACF}}$ ${\displaystyle {\overline {AC}}:{\overline {AF}}={\overline {CI}}:{\overline {IF}}}$

En , . ${\displaystyle \triangle {BCF}}$ ${\displaystyle {\overline {BC}}:{\overline {BF}}={\overline {CI}}:{\overline {IF}}}$

Por lo tanto, para que . ${\displaystyle {\overline {AC}}:{\overline {AF}}={\overline {BC}}:{\overline {BF}}}$ ${\displaystyle {\overline {AC}}:{\overline {BC}}={\overline {AF}}:{\overline {BF}}}$

Así es la bisección de ${\displaystyle {\overline {CF}}}$ ${\displaystyle \angle {ACB}}$

prueba perpendicular

Una recta que es bisectriz de un ángulo equidista de ambas rectas cuando se mide por la perpendicular. En el punto donde se cruzan dos bisectrices, este punto es perpendicularmente equidistante de las líneas que forman el ángulo final (porque están a la misma distancia del borde opuesto de este ángulo) y, por lo tanto, se encuentra en su línea bisectriz del ángulo.

Relación con los lados y vértices de un triángulo

Coordenadas trilineales

Las coordenadas trilineales de un punto del triángulo dan la razón de las distancias a los lados del triángulo. Las coordenadas trilineales para el incentro vienen dadas por ^[2]

${\displaystyle \ 1:1:1.}$

A la colección de centros de triángulos se le puede dar la estructura de un grupo mediante la multiplicación por coordenadas de coordenadas trilineales; en este grupo, el incentro forma el elemento de identidad . ^[2]

Coordenadas baricéntricas

Las coordenadas baricéntricas de un punto en un triángulo dan pesos tales que el punto es el promedio ponderado de las posiciones de los vértices del triángulo. Las coordenadas baricéntricas para el incentro están dadas por

${\displaystyle \ a:b:c}$

donde , y son las longitudes de los lados del triángulo, o equivalentemente (usando la ley de los senos ) por ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

${\displaystyle \sin(A):\sin(B):\sin(C)}$

donde , y son los ángulos en los tres vértices. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

Coordenadas cartesianas

Las coordenadas cartesianas del incentro son un promedio ponderado de las coordenadas de los tres vértices usando las longitudes de los lados del triángulo en relación con el perímetro (es decir, usando las coordenadas baricéntricas dadas anteriormente, normalizadas para sumar la unidad) como pesos. (Los pesos son positivos, por lo que el incentro se encuentra dentro del triángulo como se indicó anteriormente). Si los tres vértices están ubicados en , y , y los lados opuestos a estos vértices tienen longitudes correspondientes , y , entonces el incentro está en ${\displaystyle (x_{A},y_{A})}$ ${\displaystyle (x_{B},y_{B})}$ ${\displaystyle (x_{C},y_{C})}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

${\displaystyle {\bigg (}{\frac {ax_{A}+bx_{B}+cx_{C}}{a+b+c}},{\frac {ay_{A}+by_{B}+cy_{C}}{a+b+c}}{\bigg )}={\frac {a(x_{A},y_{A})+b(x_{B},y_{B})+c(x_{C},y_{C})}{a+b+c}}.}$

Distancias a vértices

Al denotar el incentro del triángulo ABC como I , las distancias desde el incentro a los vértices combinadas con las longitudes de los lados del triángulo obedecen a la ecuación ^[7]

${\displaystyle {\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1.}$

Además, ^[8]

${\displaystyle IA\cdot IB\cdot IC=4Rr^{2},}$

donde R y r son el circunradio y el inradio del triángulo respectivamente.

Construcciones relacionadas

Otros centros

La distancia del incentro al centroide es menos de un tercio de la longitud de la mediana más larga del triángulo. ^[9]

Según el teorema de Euler en geometría , la distancia al cuadrado desde el incentro I al circuncentro O viene dada por ^{[10] [11]}

${\displaystyle OI^{2}=R(R-2r),}$

donde R y r son el circunradio y el inradio respectivamente; por tanto, el circunradio es al menos el doble del inradio, siendo igual sólo en el caso equilátero . ^{[12] : pág. 198}

La distancia desde el incentro al centro N del círculo de nueve puntos es ^[11]

${\displaystyle IN={\frac {1}{2}}(R-2r)<{\frac {1}{2}}R.}$

La distancia al cuadrado del incentro al ortocentro H es ^[13]

${\displaystyle IH^{2}=2r^{2}-4R^{2}\cos A\cos B\cos C.}$

Las desigualdades incluyen:

${\displaystyle IG<HG,\quad IH<HG,\quad IG<IO,\quad 2IN<IO.}$

El incentro es el punto de Nagel del triángulo medial (el triángulo cuyos vértices son los puntos medios de los lados) y por lo tanto se encuentra dentro de este triángulo. Por el contrario, el punto de Nagel de cualquier triángulo es el incentro de su triángulo anticomplementario . ^[14]

El incentro debe estar en el interior de un disco cuyo diámetro conecta el centroide G y el ortocentro H (el disco ortocentroide ), pero no puede coincidir con el centro de nueve puntos , cuya posición está fijada a 1/4 del recorrido a lo largo del diámetro. (más cerca de G ). Cualquier otro punto dentro del disco ortocentroide es el incentro de un triángulo único. ^[15]

línea de euler

La recta de Euler de un triángulo es una recta que pasa por su circuncentro , centroide y ortocentro , entre otros puntos. El incentro generalmente no se encuentra en la recta de Euler; ^[16] está en la línea de Euler solo para triángulos isósceles , ^[17] para los cuales la línea de Euler coincide con el eje de simetría del triángulo y contiene todos los centros del triángulo.

Denotando la distancia desde el incentro a la recta de Euler como d , la longitud de la mediana más larga como v , la longitud del lado más largo como u , el circunradio como R , la longitud del segmento de recta de Euler desde el ortocentro al circuncentro como e , y el semiperímetro como s , se cumplen las siguientes desigualdades: ^[18]

${\displaystyle {\frac {d}{s}}<{\frac {d}{u}}<{\frac {d}{v}}<{\frac {1}{3}};}$

${\displaystyle d<{\frac {1}{3}}e;}$

${\displaystyle d<{\frac {1}{2}}R.}$

Divisores de área y perímetro

Cualquier línea que pase por un triángulo y que divida el área del triángulo y su perímetro por la mitad pasa por el incentro del triángulo; cada línea que pasa por el incentro y que divide el área por la mitad también divide el perímetro por la mitad. Hay una, dos o tres de estas líneas para cualquier triángulo dado. ^[19]

Distancias relativas desde una bisectriz de ángulo

Sea X un punto variable en la bisectriz del ángulo interno de A. Entonces X = I (el incentro) maximiza o minimiza la relación a lo largo de esa bisectriz del ángulo. ^{[20] [21]} ${\displaystyle {\tfrac {BX}{CX}}}$

Referencias

1. Kimberling, Clark (1994), "Puntos centrales y líneas centrales en el plano de un triángulo", Revista de Matemáticas , 67 (3): 163–187, doi :10.1080/0025570X.1994.11996210, JSTOR  2690608, MR  1573021.
2. de centros triangulares Archivado el 19 de abril de 2012 en Wayback Machine , consultado el 28 de octubre de 2014.
3. Elementos de Euclides , Libro IV, Proposición 4: Inscribir un círculo en un triángulo dado. David Joyce, Universidad Clark, consultado el 28 de octubre de 2014.
4. Johnson, RA (1929), Geometría moderna , Boston: Houghton Mifflin, p. 182.
5. Blum, Harry (1967), "Una transformación para extraer nuevos descriptores de forma", en Wathen-Dunn, Weiant (ed.), Modelos para la percepción del habla y la forma visual ( PDF) , Cambridge: MIT Press, págs. 362–380, en el triángulo, tres esquinas comienzan a propagarse y desaparecen en el centro del círculo inscrito más grande..
6. Aichholzer, Oswin; Aurenhammer, Franz ; Alberts, David; Gärtner, Bernd (1995), "Un nuevo tipo de esqueleto para polígonos", Journal of Universal Computer Science , 1 (12): 752–761, doi :10.1007/978-3-642-80350-5_65, MR  1392429.
7. Allaire, Patricia R.; Zhou, Junmin; Yao, Haishen (marzo de 2012), "Demostración de una identidad de elipse del siglo XIX", Mathematical Gazette , 96 : 161–165, doi :10.1017/S0025557200004277.
8. Altshiller-Court, Nathan (1980), Geometría universitaria , Publicaciones de Dover. #84, pág. 121.
9. Franzsen, William N. (2011), "La distancia desde el incentro a la línea de Euler" (PDF) , Forum Geometriorum , 11 : 231–236, MR  2877263. Lema 3, pág. 233.
10. Johnson (1929), pág. 186
11. Franzsen (2011), pág. 232.
12. Dragutin Svrtan y Darko Veljan, "Versiones no euclidianas de algunas desigualdades triangulares clásicas", Forum Geometriorum 12 (2012), 197-209. http://forumgeom.fau.edu/FG2012volume12/FG201217index.html
13. Marie-Nicole Gras, "Distancias entre el circuncentro del triángulo extouch y los centros clásicos" Forum Geometriorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html
14. Franzsen (2011), Lema 1, p. 233.
15. Franzsen (2011), pág. 232.
16. Schattschneider, Doris ; King, James (1997), Geometría activada: software dinámico en el aprendizaje, la enseñanza y la investigación, The Mathematical Association of America, págs. 3–4, ISBN 978-0883850992
17. Edmonds, Allan L.; Hajja, Mowaffaq; Martini, Horst (2008), "Orthocentric simplices and biregularity", Results in Mathematics , 52 (1–2): 41–50, doi :10.1007/s00025-008-0294-4, MR  2430410, S2CID  121434528, Está bien Se sabe que el incentro de un triángulo euclidiano se encuentra en su recta de Euler que conecta el centroide y el circuncentro si y sólo si el triángulo es isósceles..
18. Franzsen (2011), págs. 232-234.
19. Kodokostas, Dimitrios (abril de 2010), "Ecualizadores triangulares", Revista de Matemáticas , 83 (2): 141–146, doi :10.4169/002557010X482916, S2CID  218541138.
20. Arie Bialostocki y Dora Bialostocki, "El incentro y el excentro como soluciones a un problema extremo", Forum Geometriorum 11 (2011), 9-12. http://forumgeom.fau.edu/FG2011volume11/FG201102index.html
21. Hajja, Mowaffaq, Propiedades extremas del incentro y los excentros de un triángulo", Mathematical Gazette 96, julio de 2012, 315-317.

enlaces externos

• Weisstein, Eric W. "Incentro". MundoMatemático .