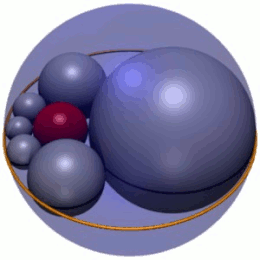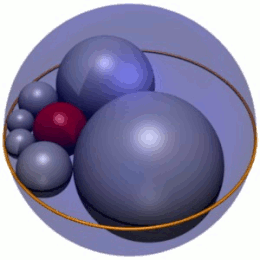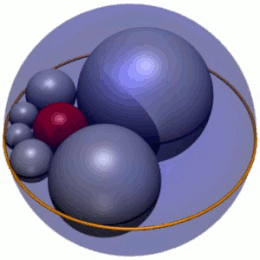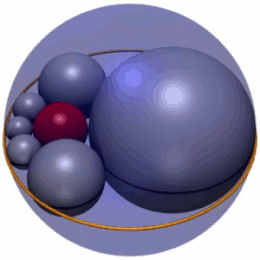
En geometría , el hexlet de Soddy es una cadena de seis esferas (mostradas en gris en la Figura 1), cada una de las cuales es tangente a sus dos vecinas y también a tres esferas dadas mutuamente tangentes. En la Figura 1, las tres esferas son la esfera interior roja y dos esferas (no mostradas) por encima y por debajo del plano en el que se encuentran los centros de las esferas del hexlet. Además, las esferas del hexlet son tangentes a una cuarta esfera (la esfera exterior azul en la Figura 1), que no es tangente a las otras tres.
Según un teorema publicado por Frederick Soddy en 1937, [1] siempre es posible encontrar un hexlet para cualquier elección de esferas mutuamente tangentes A , B y C . De hecho, existe una familia infinita de hexlets relacionados por rotación y escala de las esferas hexlet (Figura 1); en esto, el hexlet de Soddy es el análogo esférico de una cadena de Steiner de seis círculos. [2] En consonancia con las cadenas de Steiner, los centros de las esferas hexlet se encuentran en un solo plano, en una elipse. El hexlet de Soddy también fue descubierto de forma independiente en Japón, como lo muestran las tablillas de Sangaku de 1822 en la prefectura de Kanagawa. [3]
El hexlet de Soddy es una cadena de seis esferas, etiquetadas como S 1 – S 6 , cada una de las cuales es tangente a tres esferas dadas, A , B y C , que son mutuamente tangentes en tres puntos distintos. (Para mantener la coherencia en todo el artículo, las esferas hexlet siempre se representarán en gris, las esferas A y B en verde y la esfera C en azul). Las esferas hexlet también son tangentes a una cuarta esfera fija D (siempre mostrada en rojo) que no es tangente a las otras tres, A , B y C .
Cada esfera del hexágono de Soddy también es tangente a sus vecinas en la cadena; por ejemplo, la esfera S 4 es tangente a S 3 y S 5 . La cadena está cerrada, lo que significa que cada esfera en la cadena tiene dos vecinas tangentes; en particular, las esferas inicial y final, S 1 y S 6 , son tangentes entre sí.

El hexágono anular de Soddy es un caso especial (Figura 2), en el que las tres esferas mutuamente tangentes consisten en una única esfera de radio r (azul) intercalada entre dos planos paralelos (verdes) separados por una distancia perpendicular 2 r . En este caso, el hexágono de Soddy consiste en seis esferas de radio r empaquetadas como cojinetes de bolas alrededor de la esfera central y también intercaladas. Las esferas del hexágono también son tangentes a una cuarta esfera (roja), que no es tangente a las otras tres.
La cadena de seis esferas puede rotarse alrededor de la esfera central sin afectar sus tangencias, lo que demuestra que existe una familia infinita de soluciones para este caso. A medida que rotan, las esferas del hexágono trazan un toro (una superficie con forma de rosquilla); en otras palabras, un toro es la envolvente de esta familia de hexágonos.
El problema general de encontrar un hexlete para tres esferas A , B y C mutuamente tangentes se puede reducir al caso anular utilizando la inversión . Esta operación geométrica siempre transforma esferas en esferas o en planos, que pueden considerarse como esferas de radio infinito. Una esfera se transforma en un plano si y solo si la esfera pasa por el centro de inversión. Una ventaja de la inversión es que preserva la tangencia; si dos esferas son tangentes antes de la transformación, permanecen así después. Por lo tanto, si la transformación de inversión se elige juiciosamente, el problema se puede reducir a un caso más simple, como el hexlete anular de Soddy. La inversión es reversible; repetir una inversión en el mismo punto devuelve los objetos transformados a su tamaño y posición originales.
La inversión en el punto de tangencia entre las esferas A y B las transforma en planos paralelos, que pueden denotarse como a y b . Dado que la esfera C es tangente tanto a A como a B y no pasa por el centro de inversión, C se transforma en otra esfera c que es tangente a ambos planos; por lo tanto, c está intercalada entre los dos planos a y b . Este es el hexlet anular de Soddy (Figura 2). Se pueden empaquetar seis esferas s 1 – s 6 alrededor de c y también intercalarlas entre los planos límite a y b . La reinversión restaura las tres esferas originales y transforma s 1 – s 6 en un hexlet para el problema original. En general, estas esferas hexlet S 1 – S 6 tienen diferentes radios.
Se puede generar una variedad infinita de hexágonos rotando las seis bolas s 1 – s 6 en su plano en un ángulo arbitrario antes de volver a invertirlas. La envoltura producida por tales rotaciones es el toro que rodea la esfera c y está intercalado entre los dos planos a y b ; por lo tanto, el toro tiene un radio interior r y un radio exterior 3 r . Después de la reinversión, este toro se convierte en un ciclado de Dupin (Figura 3).

La envolvente de los hexletes de Soddy es un cicluro de Dupin , una inversión del toro . Por lo tanto, la construcción de Soddy muestra que un cicluro de Dupin es la envolvente de una familia de esferas de un parámetro de dos maneras diferentes, y cada esfera en cada familia es tangente a dos esferas de la misma familia y tres esferas de la otra familia. [4] Este resultado probablemente era conocido por Charles Dupin , quien descubrió los cicluros que llevan su nombre en su disertación de 1803 bajo la dirección de Gaspard Monge . [5]
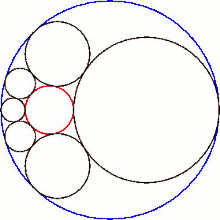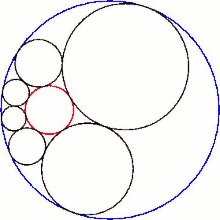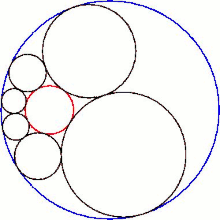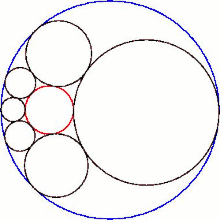
La intersección del hexágono con el plano de sus centros esféricos produce una cadena de Steiner de seis círculos.
Se supone que las esferas A y B tienen el mismo tamaño.
En cualquier hexágono elíptico , como el que se muestra en la parte superior del artículo, hay dos planos tangentes al hexágono. Para que exista un hexágono elíptico, el radio de C debe ser menor que un cuarto del de A. Si el radio de C es un cuarto del de A , cada esfera se convertirá en un plano en el recorrido. Sin embargo, la imagen invertida muestra un hexágono elíptico normal y, en el hexágono parabólico , el punto en el que una esfera se convierte en un plano es precisamente cuando su imagen invertida pasa por el centro de inversión. En un hexágono de este tipo, solo hay un plano tangente al hexágono. La línea de los centros de un hexágono parabólico es una parábola.
Si C es incluso mayor que eso, se forma un hexágono hiperbólico y ahora no hay planos tangentes en absoluto. Etiquete las esferas S 1 a S 6 . S 1, por lo tanto, no puede ir muy lejos hasta que se convierte en un plano (donde su imagen invertida pasa por el centro de inversión) y luego invierte su concavidad (donde su imagen invertida rodea el centro de inversión). Ahora la línea de los centros es una hipérbola.
El caso límite es cuando A , B y C tienen el mismo tamaño. El hexágono ahora se vuelve recto. S 1 es pequeño cuando pasa a través del agujero entre A , B y C , y crece hasta convertirse en un plano tangente a ellos. El centro de inversión ahora también tiene un punto de tangencia con la imagen de S 6 , por lo que también es un plano tangente a A , B y C. A medida que S 1 avanza, su concavidad se invierte y ahora rodea todas las demás esferas, tangentes a A , B , C , S 2 y S 6. S 2 empuja hacia arriba y crece para convertirse en un plano tangente y S 6 se encoge. S 1 obtiene entonces la posición anterior de S 6 como plano tangente. Luego invierte la concavidad nuevamente y pasa a través del agujero nuevamente, comenzando otro viaje de ida y vuelta. Ahora la línea de centros es una hipérbola degenerada , donde se ha colapsado en dos líneas rectas. [2]


Los matemáticos japoneses descubrieron el mismo hexlet más de cien años antes que Soddy. Analizaron los problemas de empaquetamiento en los que entran en contacto círculos y polígonos, bolas y poliedros y, a menudo, encontraron los teoremas relevantes de forma independiente antes de que los descubrieran los matemáticos occidentales. A menudo los publicaron como sangaku . El sangaku sobre el hexlet fue realizado por Irisawa Shintarō Hiroatsu en la escuela de Uchida Itsumi, y dedicado al Santuario Samukawa en mayo de 1822. El sangaku original se ha perdido, pero fue registrado en el libro de Uchida de Kokonsankan en 1832. Se hizo una réplica del sangaku a partir del registro y se dedicó al museo Hōtoku en el Santuario Samukawa en agosto de 2009. [6]
El sangaku de Irisawa consta de tres problemas. El tercer problema se relaciona con el hexlet de Soddy: "el diámetro de la esfera circundante exterior es 30 soles . Los diámetros de las bolas del núcleo son 10 soles y 6 soles cada una. El diámetro de una de las bolas de la cadena de bolas es 5 soles. Luego pregunté por los diámetros de las bolas restantes. La respuesta es 15 soles, 10 soles, 3,75 soles, 2,5 soles y 2 + 8/11 soles". [7]
En su respuesta, se escribe el método para calcular los diámetros de las bolas y, cuando se convierte a notación matemática , da la siguiente solución. Si las razones del diámetro de la bola exterior a cada una de las bolas del núcleo son a 1 , a 2 , y si las razones del diámetro a las bolas de la cadena son c 1 , ..., c 6 . queremos representar c 2 , ..., c 6 en términos de a 1 , a 2 y c 1 . Si
entonces,
Entonces c 1 + c 4 = c 2 + c 5 = c 3 + c 6 .
Si r 1 , ..., r 6 son los diámetros de seis bolas, obtenemos la fórmula: