Campo evanescente

Tipo de campo donde el flujo neto de energía electromagnética es cero

Representación esquemática de una onda superficial ( polaritón plasmónico superficial ) que se propaga a lo largo de una interfaz metal-dieléctrica. Los campos que se alejan de la superficie se reducen exponencialmente (gráfico de la derecha) y, por lo tanto, esos campos se describen como evanescentes en la dirección z

En electromagnetismo , un campo evanescente , u onda evanescente , es un campo eléctrico y/o magnético oscilante que no se propaga como una onda electromagnética sino que su energía se concentra espacialmente en la proximidad de la fuente (cargas y corrientes oscilantes). Incluso cuando se produce una onda electromagnética que se propaga (por ejemplo, mediante una antena transmisora ), se puede identificar como campo evanescente el componente del campo eléctrico o magnético que no se puede atribuir a la onda que se propaga observada a una distancia de muchas longitudes de onda (como el campo lejano de una antena transmisora).

Una característica distintiva de un campo evanescente es que no hay flujo neto de energía en esa región. Dado que el flujo neto de energía electromagnética está dado por el vector de Poynting promedio , esto significa que el vector de Poynting en estas regiones, promediado a lo largo de un ciclo de oscilación completo, es cero. ^[a]

Uso del término

En muchos casos no se puede decir simplemente que un campo es o no "evanescente" (es decir, que el vector de Poynting promedia cero en alguna dirección (o en todas las direcciones). En la mayoría de los casos en que existen, los campos evanescentes se consideran y se hace referencia a ellos simplemente como a todos los demás campos eléctricos o magnéticos involucrados, sin ningún reconocimiento especial de la evanescencia de esos campos. El uso del término se limita principalmente a distinguir una parte de un campo o solución en aquellos casos en los que solo se podrían esperar los campos de una onda que se propaga.

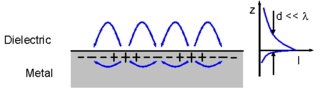
Por ejemplo, en la ilustración que aparece en la parte superior del artículo, la energía se transmite en la dirección horizontal, pero en la dirección vertical la intensidad del campo disminuye exponencialmente a medida que aumenta la distancia sobre la superficie. Esto hace que la mayor parte del campo se concentre en una fina capa límite muy cerca de la interfaz; por eso se la denomina onda superficial . ^{[1] Sin embargo, a pesar de que la energía fluye horizontalmente, a lo largo de la vertical} no hay propagación neta de energía hacia (o desde) la superficie, de modo que se podría describir correctamente el campo como "evanescente en la dirección vertical". Este es un ejemplo de la dependencia del contexto del término.

Los aparatos electrónicos y eléctricos de uso cotidiano están rodeados de grandes campos que son evanescentes; su funcionamiento implica voltajes alternos (que producen un campo eléctrico entre ellos) y corrientes alternas (que producen un campo magnético a su alrededor) que se espera que solo transporten energía a lo largo de cables internos, pero no al exterior de los dispositivos. Aunque el término "evanescente" no se menciona en este contexto ordinario, los diseñadores de los aparatos pueden estar preocupados por mantener la evanescencia, con el fin de prevenir o limitar la producción de una onda electromagnética que se propaga, lo que provocaría una pérdida de radiación , ya que una onda que se propaga "roba" su energía del circuito o dona interferencias no deseadas .

El término "campo evanescente" surge en varios contextos en los que interviene una onda electromagnética que se propaga (aunque esté confinada). El término diferencia entonces los componentes del campo electromagnético que acompañan a la onda que se propaga, pero que no se propagan por sí mismos. En otros casos similares, en los que normalmente se esperaría una onda electromagnética que se propaga (como la luz refractada en la interfaz entre el vidrio y el aire), el término se invoca para describir esa parte del campo donde la onda se suprime (como la luz que viaja a través del vidrio, incidiendo en una interfaz vidrio-aire pero más allá del ángulo crítico ).

Aunque todos los campos electromagnéticos se rigen clásicamente por las ecuaciones de Maxwell , diferentes tecnologías o problemas tienen ciertos tipos de soluciones esperadas, y cuando las soluciones primarias involucran la propagación de ondas, el término evanescente se aplica frecuentemente a componentes o soluciones de campo que no comparten esa propiedad.

Por ejemplo, la constante de propagación de una guía de ondas de metal hueco es una función importante de la frecuencia (una relación de dispersión ). Por debajo de una determinada frecuencia (la frecuencia de corte ), la constante de propagación se convierte en un número imaginario. Una solución de la ecuación de onda que tenga un número de onda imaginario no se propaga como una onda, sino que disminuye exponencialmente, por lo que el campo excitado a esa frecuencia más baja se considera evanescente. También se puede decir simplemente que la propagación está "prohibida" para esa frecuencia.

La solución formal de la ecuación de onda puede describir modos que tienen una forma idéntica, pero el cambio de la constante de propagación de real a imaginaria a medida que la frecuencia cae por debajo de la frecuencia de corte cambia totalmente la naturaleza física del resultado. La solución puede describirse como un "modo de corte" o un "modo evanescente"; ^{[2] [3] : 360} mientras que un autor diferente simplemente afirmará que no existe tal modo. Dado que el campo evanescente correspondiente al modo se calculó como una solución a la ecuación de onda, a menudo se lo analiza como una "onda evanescente" a pesar de que sus propiedades (como no transportar energía) son incompatibles con la definición de onda .

Aunque este artículo se centra en el electromagnetismo, el término evanescente se utiliza de forma similar en campos como la acústica y la mecánica cuántica , donde la ecuación de onda surge de la física implicada. En estos casos, las soluciones de la ecuación de onda que dan lugar a constantes de propagación imaginarias también se denominan "evanescentes" y tienen la propiedad esencial de que no se transfiere energía neta, aunque exista un campo distinto de cero.

Aplicaciones de las ondas evanescentes

En óptica y acústica , las ondas evanescentes se forman cuando las ondas que viajan en un medio experimentan una reflexión interna total en su límite porque lo golpean en un ángulo mayor que el ángulo crítico . ^{[4] [5]} La explicación física para la existencia de la onda evanescente es que los campos eléctrico y magnético (o gradientes de presión , en el caso de las ondas acústicas) no pueden ser discontinuos en un límite, como sería el caso si no hubiera un campo de onda evanescente. En mecánica cuántica , la explicación física es exactamente análoga: la función de onda de Schrödinger que representa el movimiento de partículas normal al límite no puede ser discontinua en el límite.

Las ondas evanescentes electromagnéticas se han utilizado para ejercer presión de radiación óptica sobre partículas pequeñas para atraparlas con fines experimentales, o para enfriarlas a temperaturas muy bajas, y para iluminar objetos muy pequeños como células biológicas o moléculas individuales de proteína y ADN para su estudio microscópico (como en el microscopio de fluorescencia de reflexión interna total ). La onda evanescente de una fibra óptica se puede utilizar en un sensor de gas, y las ondas evanescentes figuran en la técnica de espectroscopia infrarroja conocida como reflectancia total atenuada .

En ingeniería eléctrica , las ondas evanescentes se encuentran en la región de campo cercano dentro de un tercio de la longitud de onda de cualquier antena de radio. Durante el funcionamiento normal, una antena emite campos electromagnéticos en la región de campo cercano circundante y una parte de la energía del campo se reabsorbe, mientras que el resto se irradia como ondas electromagnéticas.

Recientemente, se ha fabricado una rejilla de Bragg ( cristal fotónico unidimensional) basada en grafeno y se ha demostrado su competencia para la excitación de ondas electromagnéticas superficiales en la estructura periódica utilizando una técnica de acoplamiento de prismas . ^[6]

En mecánica cuántica , las soluciones de ondas evanescentes de la ecuación de Schrödinger dan lugar al fenómeno de tunelización mecánica de ondas .

En microscopía , los sistemas que capturan la información contenida en las ondas evanescentes se pueden utilizar para crear imágenes de súper resolución . La materia irradia ondas electromagnéticas tanto propagantes como evanescentes. Los sistemas ópticos convencionales capturan solo la información en las ondas que se propagan y, por lo tanto, están sujetos al límite de difracción . Los sistemas que capturan la información contenida en las ondas evanescentes, como la superlente y la microscopía óptica de barrido de campo cercano , pueden superar el límite de difracción; sin embargo, estos sistemas están limitados por la capacidad del sistema para capturar con precisión las ondas evanescentes. ^[7] La ​​limitación de su resolución viene dada por

${\displaystyle k\propto {\frac {1}{d}}\ln {\frac {1}{\delta }},}$

donde es el vector de onda máximo que se puede resolver, es la distancia entre el objeto y el sensor, y es una medida de la calidad del sensor. ${\displaystyle k}$ ${\displaystyle d}$ ${\displaystyle \delta }$

En términos más generales, las aplicaciones prácticas de las ondas evanescentes se pueden clasificar como (1) aquellas en las que la energía asociada con la onda se utiliza para excitar algún otro fenómeno dentro de la región del espacio donde la onda viajera original se vuelve evanescente (por ejemplo, como en el microscopio de fluorescencia de reflexión interna total ) o (2) aquellas en las que la onda evanescente acopla dos medios en los que se permiten ondas viajeras y, por lo tanto, permite la transferencia de energía o una partícula entre los medios (dependiendo de la ecuación de onda en uso), aunque no se permitan soluciones de ondas viajeras en la región del espacio entre los dos medios. Un ejemplo de esto es el efecto túnel de las ondas , y se conoce generalmente como acoplamiento de ondas evanescentes .

Reflexión interna total de la luz

Reflexión interna total

Representación de una onda incidente refractada (arriba) y una onda evanescente (abajo) en una interfaz en rojo (se omiten las ondas reflejadas).

Por ejemplo, considere la reflexión interna total en dos dimensiones, con la interfaz entre los medios en el eje x, la normal a lo largo de y y la polarización a lo largo de z. Se podría esperar que para ángulos que conducen a la reflexión interna total, la solución consistiera en una onda incidente y una onda reflejada, sin onda transmitida en absoluto, pero no existe una solución que obedezca las ecuaciones de Maxwell . Las ecuaciones de Maxwell en un medio dieléctrico imponen una condición de contorno de continuidad para los componentes de los campos E _|| , H _|| , D _y y B _y . Para la polarización considerada en este ejemplo, las condiciones en E _|| y B _y se satisfacen si la onda reflejada tiene la misma amplitud que la incidente, porque estos componentes de las ondas incidente y reflejada se superponen destructivamente. Sus componentes H _x , sin embargo, se superponen constructivamente, por lo que no puede haber solución sin una onda transmitida que no se desvanezca. Sin embargo, la onda transmitida no puede ser una onda sinusoidal, ya que transportaría energía fuera del límite, pero como las ondas incidente y reflejada tienen la misma energía, esto violaría la conservación de la energía . Por lo tanto, concluimos que la onda transmitida debe ser una solución no evanescente de las ecuaciones de Maxwell que no sea una onda viajera, y las únicas soluciones de este tipo en un dieléctrico son aquellas que decaen exponencialmente: ondas evanescentes.

Matemáticamente, las ondas evanescentes se pueden caracterizar por un vector de onda en el que uno o más de los componentes del vector tienen un valor imaginario . Como el vector tiene componentes imaginarios, puede tener una magnitud menor que sus componentes reales.

Para el plano de incidencia como el plano en y la interfaz de los dos medios como el plano en , el vector de onda de la onda transmitida tiene la forma ^[8] ${\displaystyle xy}$ ${\displaystyle z=0}$ ${\displaystyle xz}$ ${\displaystyle y=0}$

${\displaystyle \mathbf {k_{t}} \ =\ k_{y}{\hat {\mathbf {y} }}+k_{x}{\hat {\mathbf {x} }}}$

con y , donde es la magnitud del vector de onda de la onda transmitida (por lo tanto el número de onda ), es el ángulo de refracción, y y son los vectores unitarios a lo largo de la dirección del eje y la dirección del eje respectivamente. ${\displaystyle k_{x}=k_{t}\sin \theta _{t}}$ ${\displaystyle k_{y}=k_{t}\cos \theta _{t}}$ ${\displaystyle k_{t}}$ ${\displaystyle \theta _{t}}$ ${\displaystyle {\hat {\mathbf {x} }}}$ ${\displaystyle {\hat {\mathbf {y} }}}$ ${\displaystyle x}$ ${\displaystyle y}$

Utilizando la ley de Snell donde , , y son el índice de refracción del medio donde existe la onda incidente y la onda reflejada, el índice de refracción del medio donde existe la onda transmitida y el ángulo de incidencia respectivamente, ${\displaystyle n_{i}\sin \theta _{i}=n_{t}\sin \theta _{t}}$ ${\displaystyle n_{i}}$ ${\displaystyle n_{t}}$ ${\displaystyle \theta _{i}}$

${\displaystyle k_{y}=k_{t}\cos \theta _{t}=\pm k_{t}\left(1-{\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}\right)^{1/2}}$.

con . ${\textstyle n_{ti}={\frac {n_{t}}{n_{i}}}}$

Si se cumple una parte de la condición de la reflexión interna total como , entonces ${\displaystyle \sin \theta _{i}>\sin \theta _{c}=n_{ti}}$

${\displaystyle k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha }$.

Si la polarización es perpendicular al plano de incidencia (a lo largo de la dirección), entonces el campo eléctrico de cualquiera de las ondas (incidente, reflejada o transmitida) se puede expresar como ${\displaystyle z}$

${\displaystyle \mathbf {E} (\mathbf {r} ,t)=\operatorname {Re} \left\{E(\mathbf {r} )e^{i\omega t}\right\}\mathbf {\hat {z}} }$

donde es el vector unitario en la dirección del eje. ${\displaystyle \mathbf {\hat {z}} }$ ${\displaystyle z}$

Suponiendo que las ondas planas son , y sustituyendo el vector de onda transmitida en , encontramos para la onda transmitida: ${\displaystyle E(\mathbf {r} )=E_{0}e^{-i\mathbf {k} \cdot \mathbf {r} }}$ ${\displaystyle \mathbf {k_{t}} }$ ${\displaystyle \mathbf {k} }$

${\displaystyle E(\mathbf {r} )=E_{o}e^{-i(-i\alpha y+\beta x)}=E_{o}e^{-\alpha y-i\beta x}}$

donde es la constante de atenuación y es la constante de fase . se ignora ya que físicamente no tiene sentido (la amplificación de onda a lo largo de la dirección y en este caso). ${\textstyle \alpha =k_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}}$ ${\displaystyle \beta =k_{x}}$ ${\displaystyle +i\alpha }$

Acoplamiento de ondas evanescentes

Gráfico de la profundidad de penetración 1/e de la onda evanescente frente al ángulo de incidencia en unidades de longitud de onda para diferentes índices de refracción.

Especialmente en óptica , el acoplamiento de ondas evanescentes se refiere al acoplamiento entre dos ondas debido a la superposición física de lo que de otro modo se describiría como los campos evanescentes correspondientes a las ondas que se propagan. ^[9]

Un ejemplo clásico es la reflexión interna total frustrada (FTIR), en la que el campo evanescente muy cercano (ver gráfico) a la superficie de un medio denso en el que una onda normalmente experimenta reflexión interna total se superpone a otro medio denso cercano. Esto altera la totalidad de la reflexión y desvía parte de la energía hacia el segundo medio.

El acoplamiento entre dos guías de ondas ópticas se puede realizar colocando los núcleos de las fibras muy cerca entre sí, de modo que el campo evanescente generado por un elemento excite una onda en la otra fibra. Esto se utiliza para producir divisores de fibra óptica y en la toma de fibra . En frecuencias de radio (e incluso ópticas), este dispositivo se denomina acoplador direccional. El dispositivo suele denominarse divisor de potencia en el caso de la transmisión y modulación por microondas.

El acoplamiento de ondas evanescentes es sinónimo de interacción de campo cercano en la teoría de campos electromagnéticos. Dependiendo de la naturaleza del elemento fuente, el campo evanescente involucrado es predominantemente eléctrico (capacitivo) o magnético (inductivo), a diferencia de las ondas (que se propagan) en el campo lejano donde estos componentes están conectados (fase idéntica, en la relación de la impedancia del espacio libre ). El acoplamiento de ondas evanescentes tiene lugar en el campo no radiativo cerca de cada medio y, como tal, siempre está asociado con la materia; es decir, con las corrientes y cargas inducidas dentro de una superficie parcialmente reflectante. En mecánica cuántica, la interacción de la función de onda puede discutirse en términos de partículas y describirse como efecto túnel cuántico .

Aplicaciones

El acoplamiento de ondas evanescentes se utiliza comúnmente en dispositivos fotónicos y nanofotónicos como sensores de guía de ondas o acopladores (ver, por ejemplo, acoplador de prisma ). ^[10]

El acoplamiento de ondas evanescentes se utiliza para excitar, por ejemplo, resonadores de microesferas dieléctricas.

El acoplamiento evanescente, como interacción de campo cercano, es una de las preocupaciones en la compatibilidad electromagnética .

Acoplamiento de fibras ópticas sin pérdidas para toma de fibras .

El acoplamiento de ondas evanescentes juega un papel importante en la explicación teórica de la transmisión óptica extraordinaria . ^[11]

El acoplamiento de ondas evanescentes se utiliza para alimentar dispositivos de forma inalámbrica. ^{[12] [13] [14]}

Un microscopio de fluorescencia de reflexión interna total utiliza la onda evanescente producida por la reflexión interna total para excitar fluoróforos cercanos a una superficie. Esto resulta útil cuando es necesario estudiar las propiedades de la superficie de muestras biológicas. ^[15]

Véase también

• Acoplamiento (electrónica)
• Onda electromagnética
• Lente plasmónica
• Metamateriales plasmónicos
• Tunelización cuántica
• Transferencia de energía resonante
• Ley de Snell
• Superlente
• Reflexión interna total
• Microscopio de fluorescencia de reflexión interna total
• Guía de ondas
• Teoría de absorción de Wheeler-Feynman

Notas

1. O bien, expresando los campos E y H como fasores , el vector de Poynting complejo tiene una parte real cero. ${\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}}$

Referencias

1. Takayama, O.; Bogdanov, AA; Lavrinenko, AV (2017). "Ondas superficiales fotónicas en interfaces metamateriales". Journal of Physics: Condensed Matter . 29 (46): 463001. Bibcode :2017JPCM...29T3001T. doi :10.1088/1361-648X/aa8bdd. PMID  29053474. S2CID  1528860.
2. Diccionario estándar IEEE de términos eléctricos y electrónicos . Nueva York, NY: Instituto de Ingenieros Eléctricos y Electrónicos . 1992. pág. 458. ISBN 978-1-55937-240-4.IEEE STD 100-1992.
3. Jackson, John David (1999). Electrodinámica clásica (3.ª ed.). John-Wiley. ISBN 047130932X.
4. Tineke Thio (2006). "Un futuro brillante para las fuentes de luz de sublongitud de onda". American Scientist . 94 (1): 40–47. doi :10.1511/2006.1.40.
5. Marston, Philip L.; Matula, TJ (mayo de 2002). "Dispersión de ondas acústicas evanescentes". Revista de la Sociedad Acústica de América . 111 (5): 2378. Código Bibliográfico :2002ASAJ..111.2378M. doi :10.1121/1.4778056.
6. Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "Excitación de ondas electromagnéticas superficiales en una rejilla de Bragg basada en grafeno". Scientific Reports . 2 : 737. Bibcode :2012NatSR...2E.737S. doi :10.1038/srep00737. PMC 3471096 . PMID  23071901. 
7. Neice, A., "Métodos y limitaciones de la obtención de imágenes de sublongitud de onda", Advances in Imaging and Electron Physics, vol. 163, julio de 2010.
8. Hecht, Eugene (2017). Óptica (quinta edición global). Pearson. Págs. 135-137. ISBN. 978-1-292-09693-3.
9. Zeng, Shuwen; Yu, Xia; Law, Wing-Cheung; Zhang, Yating; Hu, Rui; Dinh, Xuan-Quyen; Ho, Ho-Pui; Yong, Ken-Tye (2013). "Dependencia del tamaño de la resonancia de plasmón superficial mejorada con Au NP basada en la medición de fase diferencial". Sensores y actuadores B: Química . 176 : 1128–1133. Código Bibliográfico :2013SeAcB.176.1128Z. doi :10.1016/j.snb.2012.09.073.
10. Lova, Paola; Manfredi, Giovanni; Comoretto, Davide (2018). "Avances en cristales fotónicos 1D planares procesados ​​en solución funcional". Materiales ópticos avanzados . 6 (24): 1800730. doi : 10.1002/adom.201800730 . hdl : 11567/928329 . ISSN  2195-1071.
11. Fan, Zhiyuan; Zhan, Li; Hu, Xiao; Xia, Yuxing (2008). "Proceso crítico de transmisión óptica extraordinaria a través de una matriz periódica de agujeros de sublongitud de onda: acoplamiento de campo evanescente asistido por agujeros". Optics Communications . 281 (21): 5467. Bibcode :2008OptCo.281.5467F. doi :10.1016/j.optcom.2008.07.077.
12. Karalis, Aristeidis; JD Joannopoulos; Marin Soljačić (febrero de 2007). "Transferencia de energía inalámbrica eficiente y no radiactiva de rango medio". Anales de Física . 323 (1): 34. arXiv : physics/0611063 . Código Bibliográfico :2008AnPhy.323...34K. doi :10.1016/j.aop.2007.04.017. S2CID  1887505.
13. "El 'acoplamiento evanescente' podría alimentar dispositivos de forma inalámbrica", Celeste Biever, NewScientist.com, 15 de noviembre de 2006
14. La energía inalámbrica podría alimentar la electrónica industrial y de consumo – comunicado de prensa del MIT
15. Axelrod, D. (1 de abril de 1981). "Contactos célula-sustrato iluminados por fluorescencia de reflexión interna total". The Journal of Cell Biology . 89 (1): 141–145. doi :10.1083/jcb.89.1.141. PMC 2111781 . PMID  7014571. 

Enlaces externos

• Onda evanescente s
• Animación de ondas evanescentes y propagantes en Youtube.com