En astronomía , la inclinación axial , también conocida como oblicuidad , es el ángulo entre el eje de rotación de un objeto y su eje orbital , que es la línea perpendicular a su plano orbital ; equivalentemente, es el ángulo entre su plano ecuatorial y su plano orbital. [1] Se diferencia de la inclinación orbital .
En una oblicuidad de 0 grados, los dos ejes apuntan en la misma dirección; es decir, el eje de rotación es perpendicular al plano orbital.
El eje de rotación de la Tierra , por ejemplo, es la línea imaginaria que pasa por el Polo Norte y el Polo Sur , mientras que el eje orbital de la Tierra es la línea perpendicular al plano imaginario a través del cual se mueve la Tierra mientras gira alrededor del Sol ; la oblicuidad o inclinación axial de la Tierra es el ángulo entre estas dos líneas.
A lo largo de un período orbital , la oblicuidad no suele cambiar considerablemente y la orientación del eje permanece igual en relación con el fondo de estrellas . Esto hace que un polo apunte más hacia el Sol en un lado de la órbita y más lejos del Sol en el otro lado, lo que provoca las estaciones en la Tierra.
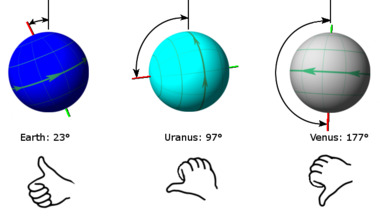
Existen dos métodos estándar para especificar la inclinación de un planeta. Una forma se basa en el polo norte del planeta , definido en relación con la dirección del polo norte de la Tierra, y la otra forma se basa en el polo positivo del planeta , definido por la regla de la mano derecha :
El plano orbital de la Tierra se conoce como plano eclíptico , y la inclinación de la Tierra es conocida por los astrónomos como la oblicuidad de la eclíptica , siendo el ángulo entre la eclíptica y el ecuador celeste en la esfera celeste . [6] Se denota con la letra griega Epsilon ε .
La Tierra tiene actualmente una inclinación axial de aproximadamente 23,44°. [7] Este valor permanece aproximadamente igual en relación con un plano orbital estacionario a lo largo de los ciclos de precesión axial . [8] Pero la eclíptica (es decir, la órbita de la Tierra) se mueve debido a perturbaciones planetarias , y la oblicuidad de la eclíptica no es una cantidad fija. En la actualidad, está disminuyendo a un ritmo de aproximadamente 46,8″ [9] por siglo (ver detalles en Corto plazo a continuación) .
Los antiguos griegos tenían buenas mediciones de la oblicuidad desde aproximadamente el año 350 a. C., cuando Piteas de Marsella midió la sombra de un gnomon en el solsticio de verano. [10] Alrededor del año 830 d. C., el califa Al-Mamun de Bagdad ordenó a sus astrónomos que midieran la oblicuidad, y el resultado se utilizó en el mundo árabe durante muchos años. [11] En 1437, Ulugh Beg determinó la inclinación axial de la Tierra en 23°30′17″ (23,5047°). [12]
Durante la Edad Media , se creía ampliamente que tanto la precesión como la oblicuidad de la Tierra oscilaban alrededor de un valor medio, con un período de 672 años, una idea conocida como trepidación de los equinoccios. Quizás el primero en darse cuenta de que esto era incorrecto (durante el tiempo histórico) fue Ibn al-Shatir en el siglo XIV [13] y el primero en darse cuenta de que la oblicuidad está disminuyendo a un ritmo relativamente constante fue Fracastoro en 1538. [14] Las primeras observaciones occidentales precisas y modernas de la oblicuidad fueron probablemente las de Tycho Brahe de Dinamarca , alrededor de 1584, [15] aunque las observaciones de varios otros, incluidos al-Ma'mun , al-Tusi , [16] Purbach , Regiomontanus y Walther , podrían haber proporcionado información similar.

El eje de la Tierra permanece inclinado en la misma dirección con respecto a las estrellas de fondo durante todo un año (independientemente de dónde se encuentre en su órbita ) debido al efecto giroscopio . Esto significa que un polo (y el hemisferio asociado de la Tierra ) se dirigirá lejos del Sol en un lado de la órbita, y media órbita más tarde (medio año después) este polo se dirigirá hacia el Sol. Esta es la causa de las estaciones de la Tierra . El verano ocurre en el hemisferio norte cuando el polo norte está dirigido hacia el Sol. Las variaciones en la inclinación axial de la Tierra pueden influir en las estaciones y es probable que sea un factor en el cambio climático a largo plazo (ver también ciclos de Milankovitch ) .

El valor angular exacto de la oblicuidad se obtiene mediante la observación de los movimientos de la Tierra y los planetas a lo largo de muchos años. Los astrónomos producen nuevas efemérides fundamentales a medida que mejora la precisión de la observación y aumenta la comprensión de la dinámica , y a partir de estas efemérides se derivan diversos valores astronómicos, incluida la oblicuidad.
Se publican almanaques anuales que enumeran los valores derivados y los métodos de uso. Hasta 1983, el valor angular de la oblicuidad media del Almanaque Astronómico para cualquier fecha se calculaba basándose en el trabajo de Newcomb , quien analizó las posiciones de los planetas hasta aproximadamente 1895:
donde ε es la oblicuidad y T son los siglos tropicales desde B1900.0 hasta la fecha en cuestión. [17]
A partir de 1984, la serie DE de efemérides generadas por ordenador del Laboratorio de Propulsión a Chorro pasó a ser la efeméride fundamental del Almanaque Astronómico . La oblicuidad basada en DE200, que analizó las observaciones realizadas entre 1911 y 1979, se calculó:
donde de aquí en adelante T son siglos julianos a partir de J2000.0 . [18]
Las efemérides fundamentales del JPL se han actualizado continuamente. Por ejemplo, según la resolución de la UAI de 2006 a favor del modelo astronómico P03, el Almanaque Astronómico de 2010 especifica: [19]
Estas expresiones para la oblicuidad están pensadas para una alta precisión en un lapso de tiempo relativamente corto, quizás ± varios siglos. [20] Jacques Laskar calculó una expresión para ordenar T 10 con un valor de 0,02″ durante 1000 años y varios segundos de arco durante 10 000 años.
donde aquí t son múltiplos de 10.000 años julianos a partir de J2000.0 . [21]
Estas expresiones corresponden a la denominada oblicuidad media , es decir, la oblicuidad libre de variaciones de corto plazo. Los movimientos periódicos de la Luna y de la Tierra en su órbita provocan oscilaciones de corto período (unos 18,6 años) mucho más pequeñas (9,2 segundos de arco ) del eje de rotación de la Tierra, conocidas como nutación , que añaden un componente periódico a la oblicuidad de la Tierra. [22] [23] La oblicuidad verdadera o instantánea incluye esta nutación. [24]
Utilizando métodos numéricos para simular el comportamiento del Sistema Solar durante un período de varios millones de años, se han investigado los cambios a largo plazo en la órbita de la Tierra y, por lo tanto, su oblicuidad. Durante los últimos 5 millones de años, la oblicuidad de la Tierra ha variado entre 22°2′33″ y 24°30′16″ , con un período medio de 41.040 años. Este ciclo es una combinación de precesión y el término más grande en el movimiento de la eclíptica . Durante el próximo millón de años, el ciclo llevará la oblicuidad entre 22°13′44″ y 24°20′50″ . [25]
La Luna tiene un efecto estabilizador sobre la oblicuidad de la Tierra. El análisis de mapas de frecuencias realizado en 1993 sugirió que, en ausencia de la Luna, la oblicuidad podría cambiar rápidamente debido a las resonancias orbitales y al comportamiento caótico del Sistema Solar , alcanzando un máximo de 90° en tan solo unos pocos millones de años ( ver también Órbita de la Luna ). [26] [27] Sin embargo, simulaciones numéricas más recientes [28] realizadas en 2011 indicaron que incluso en ausencia de la Luna, la oblicuidad de la Tierra podría no ser tan inestable; variando solo alrededor de 20-25°. Para resolver esta contradicción, se ha calculado la tasa de difusión de la oblicuidad, y se encontró que se necesitan más de miles de millones de años para que la oblicuidad de la Tierra alcance cerca de 90°. [29] El efecto estabilizador de la Luna continuará durante menos de dos mil millones de años. A medida que la Luna continúa alejándose de la Tierra debido a la aceleración de las mareas , pueden producirse resonancias que causarán grandes oscilaciones de la oblicuidad. [30]
Los cuatro planetas rocosos más interiores del Sistema Solar pueden haber tenido grandes variaciones de su oblicuidad en el pasado. Dado que la oblicuidad es el ángulo entre el eje de rotación y la dirección perpendicular al plano orbital, cambia a medida que cambia el plano orbital debido a la influencia de otros planetas. Pero el eje de rotación también puede moverse ( precesión axial ), debido al par ejercido por el Sol sobre el abultamiento ecuatorial de un planeta. Al igual que la Tierra, todos los planetas rocosos muestran precesión axial. Si la tasa de precesión fuera muy rápida, la oblicuidad en realidad permanecería bastante constante incluso cuando cambia el plano orbital. [32] La tasa varía debido a la disipación de mareas y la interacción núcleo - manto , entre otras cosas. Cuando la tasa de precesión de un planeta se acerca a ciertos valores, las resonancias orbitales pueden causar grandes cambios en la oblicuidad. La amplitud de la contribución que tiene una de las tasas de resonancia se divide por la diferencia entre la tasa de resonancia y la tasa de precesión, por lo que se vuelve grande cuando las dos son similares. [32]
Es muy probable que Mercurio y Venus hayan sido estabilizados por la disipación de marea del Sol. La Tierra fue estabilizada por la Luna, como se mencionó anteriormente, pero antes de su formación , la Tierra también podría haber pasado por períodos de inestabilidad. La oblicuidad de Marte es bastante variable a lo largo de millones de años y puede estar en un estado caótico; varía tanto como 0° a 60° a lo largo de algunos millones de años, dependiendo de las perturbaciones de los planetas. [26] [33] Algunos autores disputan que la oblicuidad de Marte sea caótica, y muestran que la disipación de marea y el acoplamiento viscoso núcleo-manto son adecuados para que haya alcanzado un estado completamente amortiguado, similar a Mercurio y Venus. [3] [34]
Se ha sugerido que los cambios ocasionales en la inclinación axial de Marte podrían explicar la aparición y desaparición de ríos y lagos a lo largo de la existencia de Marte. Un cambio podría causar una explosión de metano en la atmósfera, lo que provocaría un calentamiento, pero luego el metano se destruiría y el clima se volvería árido nuevamente. [35] [36]
Las oblicuidades de los planetas exteriores se consideran relativamente estables.
La oblicuidad estelar ψ s , es decir, la inclinación axial de una estrella con respecto al plano orbital de uno de sus planetas, se ha determinado solo para unos pocos sistemas. Hasta 2012, se ha observado una desalineación de giro-órbita proyectada en el cielo λ en 49 estrellas, [39] que sirve como límite inferior para ψ s . La mayoría de estas mediciones se basan en el efecto Rossiter-McLaughlin . Desde el lanzamiento de telescopios espaciales como el telescopio espacial Kepler , se ha hecho posible determinar y estimar la oblicuidad de un planeta extrasolar. El aplanamiento rotacional del planeta y el séquito de lunas y/o anillos, que se pueden rastrear con fotometría de alta precisión, proporcionan acceso a la oblicuidad planetaria, ψ p . Desde entonces se ha determinado la oblicuidad de muchos planetas extrasolares, como Kepler-186f y Kepler-413b . [40] [41]
Los astrofísicos han aplicado teorías de mareas para predecir la oblicuidad de los planetas extrasolares . Se ha demostrado que las oblicuidades de los exoplanetas en la zona habitable alrededor de estrellas de baja masa tienden a erosionarse en menos de 10 9 años, [42] [43] lo que significa que no tendrían estaciones inducidas por la inclinación como las tiene la Tierra.