El ecuante (o punctum aequans ) es un concepto matemático desarrollado por Claudio Ptolomeo en el siglo II d. C. para explicar el movimiento observado de los planetas. El ecuante se utiliza para explicar el cambio de velocidad observado en diferentes etapas de la órbita planetaria. Este concepto planetario permitió a Ptolomeo mantener viva la teoría del movimiento circular uniforme al afirmar que la trayectoria de los cuerpos celestes era uniforme alrededor de un punto y circular alrededor de otro punto.
Ptolomeo no tiene una palabra para el ecuante: utilizó expresiones como "el ecentro que produce el movimiento medio". [1]
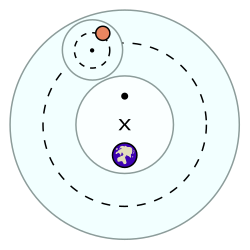
El punto ecuante (mostrado en el diagrama por el gran • ), se coloca de manera que esté directamente opuesto a la Tierra desde el centro del deferente , conocido como el excéntrico (representado por el × ). Un planeta o el centro de un epiciclo (un círculo más pequeño que lleva el planeta) fue concebido para moverse a una velocidad angular constante con respecto al ecuante. Para un observador hipotético colocado en el punto ecuante, el centro del epiciclo (indicado por el pequeño · ) parecería moverse a una velocidad angular constante. Sin embargo, el centro del epiciclo no se moverá a una velocidad constante a lo largo de su deferente. [2]
La razón para la implementación del ecuante fue mantener una apariencia de movimiento circular constante de los cuerpos celestes , un antiguo artículo de fe originado por Aristóteles por razones filosóficas, permitiendo al mismo tiempo la mejor coincidencia de los cálculos de los movimientos observados de los cuerpos, particularmente en el tamaño del aparente movimiento retrógrado de todos los cuerpos del Sistema Solar excepto el Sol y la Luna .
El modelo ecuante tiene un cuerpo en movimiento en una trayectoria circular que no tiene como centro la Tierra. La velocidad del objeto en movimiento variará durante su órbita alrededor del círculo exterior (línea discontinua), más rápido en la mitad inferior y más lento en la mitad superior, pero el movimiento se considera uniforme porque el planeta recorre ángulos iguales en tiempos iguales desde la perspectiva del punto ecuante. La velocidad angular del objeto no es uniforme cuando se observa desde cualquier otro punto dentro de la órbita.
Aplicado sin un epiciclo (como para el Sol), el uso de un ecuante permite que la velocidad angular sea correcta en el perigeo y el apogeo, con una relación de (donde es la excentricidad orbital ). Pero comparado con la órbita kepleriana , el método ecuante hace que el cuerpo pase muy poco tiempo lejos de la Tierra y demasiado cerca de ella. Por ejemplo, cuando la anomalía excéntrica es π/2, el modelo kepleriano dice que habrá transcurrido una cantidad de tiempo de desde el perigeo (donde el período es , véase la ecuación de Kepler ), mientras que el modelo ecuante da que es un poco más. Además, la verdadera anomalía en este punto, según el modelo ecuante, será solo mientras que en el modelo kepleriano es que es más. Sin embargo, para una excentricidad pequeña, el error es muy pequeño, siendo asintótico a la excentricidad a la tercera potencia.
El ángulo α cuyo vértice está en el centro del deferente y cuyos lados intersecan al planeta y al ecuante, respectivamente, es una función del tiempo t de la siguiente manera:
donde Ω es la velocidad angular constante vista desde el ecuante que está situado a una distancia E cuando el radio del deferente es R . [3]
Ptolomeo introdujo el ecuante en el " Almagesto ". [4] La evidencia de que el ecuante era un ajuste necesario a la física aristotélica se basaba en observaciones realizadas por él mismo y un tal "Teón" (quizás, Teón de Esmirna ). [2]
En los modelos de movimiento planetario que anteceden a Ptolomeo , generalmente atribuidos a Hiparco , los excéntricos y los epiciclos ya eran una característica. El escritor romano Plinio en el siglo I d.C., que aparentemente tuvo acceso a escritos de astrónomos griegos tardíos, y no siendo astrónomo él mismo, todavía identificó correctamente las líneas de ábsides para los cinco planetas conocidos y hacia dónde apuntaban en el zodíaco. [5] Tales datos requieren el concepto de centros excéntricos de movimiento.
Antes del año 430 a. C., Metón y Euctemón de Atenas observaron diferencias en la duración de las estaciones . [2] Esto se puede observar en la duración de las estaciones, dada por los equinoccios y solsticios que indican cuándo el Sol recorre 90 grados a lo largo de su trayectoria. Aunque otros lo intentaron, Hiparco calculó y presentó las duraciones más exactas de las estaciones alrededor del año 130 a. C.
Según estos cálculos, la primavera duró aproximadamente 94 +1/ 2 días , verano alrededor de 92+1/ 2 , Otoño alrededor del 88+1/ 8 , y el invierno alrededor de los 90+1/ 8 , lo que demuestra que las estaciones tenían, en efecto, diferencias de duración. Esto se utilizó más tarde como prueba de la desigualdad zodiacal, o la apariencia de que el Sol se mueve a un ritmo que no es constante, con algunas partes de su órbita, incluido él, moviéndose más rápido o más lento. El movimiento anual del Sol tal como lo entendía la astronomía griega hasta este punto no explicaba esto, ya que asumía que el Sol tenía una órbita perfectamente circular centrada alrededor de la Tierra, alrededor de la cual viajaba a una velocidad constante. Según el astrónomo Hiparco, mover el centro de la trayectoria del Sol ligeramente lejos de la Tierra satisfaría el movimiento observado del Sol sin demasiados problemas, lo que haría que la órbita del Sol fuera excéntrica. [2]
La mayor parte de lo que sabemos sobre Hiparco nos llega a través de citas de sus obras por parte de Ptolomeo. [4] Las características de los modelos de Hiparco explicaban las diferencias en la duración de las estaciones en la Tierra (conocida como la "primera anomalía") y la aparición de movimiento retrógrado en los planetas (conocida como la "segunda anomalía"). Pero Hiparco no pudo hacer que las predicciones sobre la ubicación y la duración de los movimientos retrógrados de los planetas coincidieran con las observaciones; podía acertar con la ubicación o con la duración, pero no con ambas simultáneamente. [6]
Entre el modelo de Hiparco y el de Ptolomeo se propuso un modelo intermedio para explicar el movimiento de los planetas en general basándose en el movimiento observado de Marte. En este modelo, el deferente tenía un centro que también era el ecuante, que podía moverse a lo largo de la línea de simetría del deferente para que coincidiera con el movimiento retrógrado de un planeta. Sin embargo, este modelo todavía no se alineaba con el movimiento real de los planetas, como señaló Hiparco. Esto era cierto específicamente con respecto al espaciamiento y ancho reales de los arcos retrógrados, que se pudieron ver más tarde según el modelo de Ptolomeo y comparar. [2]
El propio Ptolomeo rectificó esta contradicción al introducir el ecuante en sus escritos [4] cuando lo separó del centro del deferente, haciendo que tanto éste como el centro del deferente fueran partes distintas del modelo y haciendo que el centro del deferente fuera estacionario durante todo el movimiento de un planeta. [2] La ubicación estaba determinada por el deferente y el epiciclo, mientras que la duración estaba determinada por el movimiento uniforme alrededor del ecuante. Hizo esto sin mucha explicación o justificación de cómo llegó al punto de su creación, decidiendo solo presentarlo formalmente y concisamente con pruebas como en cualquier publicación científica. Incluso en sus trabajos posteriores, donde reconoció la falta de explicación, no hizo ningún esfuerzo por explicar más. [2]
El modelo astronómico de Ptolomeo se utilizó como método técnico que podía responder a preguntas sobre astrología y predecir las posiciones de los planetas durante casi 1.500 años, aunque muchos astrónomos posteriores consideraron que el ecuante y el excéntrico violaban la física aristotélica pura , que presumía que todo movimiento tenía su centro en la Tierra. Se ha informado de que el modelo del cosmos de Ptolomeo fue tan popular y revolucionario que, de hecho, suele ser muy difícil encontrar detalles de modelos utilizados anteriormente, salvo en los escritos del propio Ptolomeo. [2]
Durante muchos siglos, la rectificación de estas violaciones fue una preocupación entre los eruditos, que culminó con las soluciones de Ibn al-Shatir y Copérnico . Las predicciones de Ptolomeo, que requirieron constante revisión y correcciones por parte de eruditos interesados a lo largo de esos siglos, culminaron en las observaciones de Tycho Brahe en Uraniborg .
No fue hasta que Johannes Kepler publicó su Astronomia Nova , basada en los datos que él y Tycho recogieron en Uraniborg, que el modelo de los cielos de Ptolomeo fue totalmente reemplazado por un nuevo modelo geométrico. [7] [8]
El ecuante resolvió el último gran problema de explicar el movimiento anómalo de los planetas, pero algunos creían que ponía en peligro los principios de los antiguos filósofos griegos, es decir, el movimiento circular uniforme alrededor de la Tierra. [9] En general, se suponía que la uniformidad se observaba desde el centro del deferente y, dado que eso ocurre en un solo punto, solo se observa movimiento no uniforme desde cualquier otro punto. Ptolomeo desplazó el punto de observación desde el centro del deferente hasta el punto ecuante. Esto puede verse como una violación del axioma del movimiento circular uniforme.
Entre los críticos más destacados del ecuante se encuentran el astrónomo persa Nasir al-Din Tusi , que desarrolló el par de Tusi como explicación alternativa, [10] y Nicolás Copérnico , cuya alternativa era un nuevo par de pequeños epiciclos para cada deferente. El rechazo al ecuante fue una de las principales motivaciones de Copérnico para construir su sistema heliocéntrico. [11] [12]
La violación del movimiento circular uniforme alrededor del centro del deferente molestó a muchos pensadores, especialmente a Copérnico, quien menciona el ecuante como una "construcción monstruosa" en De Revolutionibus . El desplazamiento de Copérnico de la Tierra desde el centro del cosmos obviaba la necesidad primaria de los epiciclos de Ptolomeo: explicaba el movimiento retrógrado como un efecto de la perspectiva, debido al movimiento relativo de la Tierra y los planetas. Sin embargo, no explicaba el movimiento no uniforme del Sol y la Luna, cuyos movimientos relativos Copérnico no cambió (aunque sí reformuló el Sol orbitando la Tierra como la Tierra orbitando el Sol, los dos son geométricamente equivalentes). Mover el centro del movimiento planetario de la Tierra al Sol no eliminó la necesidad de algo para explicar el movimiento no uniforme del Sol, para lo cual Copérnico sustituyó dos (o varios) epiciclos más pequeños en lugar de un ecuante.