ecuación rígida

Ecuación diferencial que muestra una inestabilidad inusual

En matemáticas , una ecuación rígida es una ecuación diferencial para la cual ciertos métodos numéricos para resolver la ecuación son numéricamente inestables , a menos que se considere que el tamaño del paso es extremadamente pequeño. Ha resultado difícil formular una definición precisa de rigidez, pero la idea principal es que la ecuación incluye algunos términos que pueden conducir a una rápida variación en la solución.

Al integrar numéricamente una ecuación diferencial, se esperaría que el tamaño de paso requerido fuera relativamente pequeño en una región donde la curva solución muestra mucha variación y que fuera relativamente grande donde la curva solución se endereza para aproximarse a una línea con pendiente cercana a cero. Para algunos problemas este no es el caso. Para que un método numérico dé una solución confiable al sistema diferencial, a veces se requiere que el tamaño del paso esté en un nivel inaceptablemente pequeño en una región donde la curva de solución es muy suave. El fenómeno se conoce como rigidez . En algunos casos puede haber dos problemas diferentes con la misma solución, pero uno no es rígido y el otro sí. Por tanto, el fenómeno no puede ser una propiedad de la solución exacta, ya que ésta es la misma para ambos problemas, y debe ser una propiedad del propio sistema diferencial. Por tanto, estos sistemas se conocen como sistemas rígidos .

Ejemplo motivador

Métodos numéricos explícitos que muestran inestabilidad al integrar una ecuación diferencial ordinaria rígida

Considere el problema del valor inicial.

La solución exacta (mostrada en cian) es

Buscamos una solución numérica que muestre el mismo comportamiento.

La figura (derecha) ilustra los problemas numéricos de varios integradores numéricos aplicados a la ecuación.

1. El método de Euler con un tamaño de paso de oscila violentamente y rápidamente sale del rango del gráfico (que se muestra en rojo). ${\displaystyle h={\tfrac {1}{4}}}$
2. El método de Euler con la mitad del tamaño del paso, produce una solución dentro de los límites del gráfico, pero oscila alrededor de cero (se muestra en verde). ${\displaystyle h={\tfrac {1}{8}}}$
3. El método trapezoidal (es decir, el método Adams-Moulton de dos etapas ) viene dado por
   dónde . La aplicación de este método en lugar del método de Euler da un resultado mucho mejor (azul). Los resultados numéricos disminuyen monótonamente hasta cero, tal como lo hace la solución exacta. ${\displaystyle y'=f(t,y)}$

Uno de los ejemplos más destacados de ecuaciones diferenciales ordinarias rígidas (EDO) es un sistema que describe la reacción química de Robertson: ^[1]

Si se trata este sistema en un intervalo corto, por ejemplo, no hay problema en la integración numérica. Sin embargo, si el intervalo es muy grande (digamos 10 ¹¹ ), muchos códigos estándar no logran integrarlo correctamente. ${\displaystyle t\in [0,40]}$

Ejemplos adicionales son los conjuntos de EDO resultantes de la integración temporal de grandes mecanismos de reacción química. Aquí, la rigidez surge de la coexistencia de reacciones muy lentas y muy rápidas. ^{[ cita necesaria ]} Para resolverlos, se pueden utilizar los paquetes de software KPP y Autochem .

Relación de rigidez

Considere el sistema no homogéneo de coeficiente constante lineal.

donde y es una matriz constante, diagonalizable, con valores propios (se suponen distintos) y vectores propios correspondientes . La solución general de ( 5 ) toma la forma ${\displaystyle \mathbf {y} ,\mathbf {f} \in \mathbb {R} ^{n}}$ ${\displaystyle \mathbf {A} }$ ${\displaystyle n\times n}$ ${\displaystyle \lambda _{t}\in \mathbb {C} ,t=1,2,\ldots ,n}$ ${\displaystyle \mathbf {c} _{t}\in \mathbb {C} ^{n},t=1,2,\ldots ,n}$

donde son constantes arbitrarias y es una integral particular. Ahora supongamos que ${\displaystyle \kappa _{t}}$ ${\displaystyle \mathbf {g} (x)}$

lo que implica que cada uno de los términos es as , de modo que la solución se aproxima asintóticamente a as ; el término decaerá monótonamente si es real y sinusoidalmente si es complejo. ${\displaystyle e^{\lambda _{t}x}\mathbf {c} _{t}\to 0}$ ${\displaystyle x\to \infty }$ ${\displaystyle \mathbf {y} (x)}$ ${\displaystyle \mathbf {g} (x)}$ ${\displaystyle x\to \infty }$ ${\displaystyle e^{\lambda _{t}x}\mathbf {c} _{t}}$ ${\displaystyle \lambda _{t}}$ ${\displaystyle \lambda _{t}}$

La interpretación como tiempo (como suele ocurrir en los problemas físicos) se denomina solución transitoria y solución de estado estacionario . Si es grande, entonces el término correspondiente decaerá rápidamente a medida que aumente y, por lo tanto, se denomina transitorio rápido ; Si es pequeño, el término correspondiente decae lentamente y se denomina transitorio lento . Dejemos definir por ${\displaystyle x}$ ${\textstyle \sum _{t=1}^{n}\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}}$ ${\displaystyle \mathbf {g} (x)}$ ${\displaystyle \left|\operatorname {Re} (\lambda _{t})\right|}$ ${\displaystyle \kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}}$ ${\displaystyle x}$ ${\displaystyle \left|\operatorname {Re} (\lambda _{t})\right|}$ ${\displaystyle \kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}}$ ${\displaystyle {\overline {\lambda }},{\underline {\lambda }}\in \{\lambda _{t},t=1,2,\ldots ,n\}}$

entonces ese es el transitorio más rápido y el más lento. Ahora definimos la relación de rigidez como ^[2] ${\displaystyle \kappa _{t}e^{{\overline {\lambda }}x}\mathbf {c} _{t}}$ ${\displaystyle \kappa _{t}e^{{\underline {\lambda }}x}\mathbf {c} _{t}}$

Caracterización de la rigidez.

En esta sección consideramos varios aspectos del fenómeno de la rigidez. "Fenómeno" es probablemente una palabra más apropiada que "propiedad", ya que esta última implica que la rigidez puede definirse en términos matemáticos precisos; resulta que no es posible hacer esto de manera satisfactoria, incluso para la clase restringida de sistemas lineales de coeficientes constantes. También veremos varias afirmaciones cualitativas que pueden hacerse (y en su mayoría se han hecho) en un intento de resumir la noción de rigidez y exponer la que probablemente sea la más satisfactoria de ellas como una "definición" de rigidez.

JD Lambert define la rigidez de la siguiente manera:

Si un método numérico con una región finita de estabilidad absoluta , aplicado a un sistema con cualesquiera condiciones iniciales , se ve obligado a utilizar en un determinado intervalo de integración una longitud de paso excesivamente pequeña en relación con la suavidad de la solución exacta en ese intervalo , entonces se dice que el sistema es rígido en ese intervalo.

Hay otras características que exhiben muchos ejemplos de problemas de rigidez, pero para cada uno hay contraejemplos, por lo que estas características no constituyen buenas definiciones de rigidez. No obstante, algunos autores utilizan comúnmente definiciones basadas en estas características y son buenas pistas sobre la presencia de rigidez. Lambert se refiere a ellas como "declaraciones" en lugar de definiciones, por las razones antes mencionadas. Algunos de estos son:

1. Un sistema lineal de coeficientes constantes es rígido si todos sus valores propios tienen parte real negativa y la relación de rigidez es grande.
2. La rigidez ocurre cuando los requisitos de estabilidad, más que los de precisión, limitan la longitud del paso.
3. La rigidez ocurre cuando algunos componentes de la solución se descomponen mucho más rápidamente que otros. ^[3]

Etimología

El origen del término "rigidez" no ha sido claramente establecido. Según Joseph Oakland Hirschfelder , el término "rígido" se utiliza porque este tipo de sistemas corresponden a un acoplamiento estrecho entre el conductor y el conducido en servomecanismos . ^[4] Según Ricardo. L. Burden y J. Douglas Faires,

Pueden ocurrir dificultades significativas cuando se aplican técnicas numéricas estándar para aproximar la solución de una ecuación diferencial cuando la solución exacta contiene términos de la forma , donde es un número complejo con parte real negativa. ${\displaystyle e^{\lambda t}}$ ${\displaystyle \lambda }$

. . .

Los problemas que involucran soluciones transitorias de rápida descomposición ocurren naturalmente en una amplia variedad de aplicaciones, incluido el estudio de sistemas de resortes y amortiguación, el análisis de sistemas de control y problemas de cinética química . Todos estos son ejemplos de una clase de problemas llamados sistemas rígidos (rigidez matemática) de ecuaciones diferenciales, debido a su aplicación en el análisis del movimiento de sistemas de masa y resortes que tienen constantes elásticas grandes ( rigidez física ). ^[5]

Por ejemplo, el problema del valor inicial

con , , , se puede escribir en la forma ( 5 ) con y ${\displaystyle m=1}$ ${\displaystyle c=1001}$ ${\displaystyle k=1000}$ ${\displaystyle n=2}$

y tiene valores propios . Ambos valores propios tienen parte real negativa y la relación de rigidez es ${\displaystyle {\overline {\lambda }}=-1000,{\underline {\lambda }}=-1}$

que es bastante grande. Entonces el sistema ( 10 ) ciertamente satisface los enunciados 1 y 3. Aquí la constante elástica es grande y la constante de amortiguación es aún mayor. ^[6] (aunque "grande" no es un término claramente definido, pero cuanto mayores sean las cantidades anteriores, más pronunciado será el efecto de la rigidez). La solución exacta de ( 10 ) es ${\displaystyle k}$ ${\displaystyle c}$

La ecuación 13 se comporta de manera bastante similar a una exponencial simple , pero la presencia del término, incluso con un coeficiente pequeño, es suficiente para hacer que el cálculo numérico sea muy sensible al tamaño del paso. La integración estable de ( 10 ) requiere un tamaño de paso muy pequeño hasta bien entrada la parte suave de la curva de solución, lo que resulta en un error mucho menor que el requerido para la precisión. Por tanto, el sistema también satisface el enunciado 2 y la definición de Lambert. ${\displaystyle x_{0}e^{-t}}$ ${\displaystyle e^{-1000t}}$

A-estabilidad

El comportamiento de los métodos numéricos en problemas rígidos se puede analizar aplicando estos métodos a la ecuación de prueba sujeta a la condición inicial con . La solución de esta ecuación es . Esta solución tiende a cero como cuando . Si el método numérico también muestra este comportamiento (para un tamaño de paso fijo), entonces se dice que el método es A-estable. ^[7] Un método numérico que es L-estable (ver más abajo) tiene la propiedad más fuerte de que la solución se acerca a cero en un solo paso cuando el tamaño del paso llega al infinito. Los métodos A-estables no presentan los problemas de inestabilidad descritos en el ejemplo motivador. ${\displaystyle y'=ky}$ ${\displaystyle y(0)=1}$ ${\displaystyle k\in \mathbb {C} }$ ${\displaystyle y(t)=e^{kt}}$ ${\displaystyle t\to \infty }$ ${\displaystyle \operatorname {Re} (k)<0.}$

Métodos de Runge-Kutta

Los métodos de Runge-Kutta aplicados a la ecuación de prueba toman la forma y, por inducción ,. La función se llama función de estabilidad . Por tanto, la condición de que as es equivalente a . Esto motiva la definición de la región de estabilidad absoluta (a veces denominada simplemente región de estabilidad ), que es el conjunto . El método es A-estable si la región de estabilidad absoluta contiene el conjunto , es decir, el semiplano izquierdo. ${\displaystyle y'=k\cdot y}$ ${\displaystyle y_{n+1}=\phi (hk)\cdot y_{n}}$ ${\displaystyle y_{n}={\bigl (}\phi (hk){\bigr )}^{n}\cdot y_{0}}$ ${\displaystyle \phi }$ ${\displaystyle y_{n}\to 0}$ ${\displaystyle n\to \infty }$ ${\displaystyle |\phi (hk)|<1}$ ${\displaystyle {\bigl \{}z\in \mathbb {C} \,{\big |}\,|\phi (z)|<1{\bigr \}}}$ ${\displaystyle {\bigl \{}z\in \mathbb {C} \,{\big |}\,\operatorname {Re} (z)<0{\bigr \}}}$

Ejemplo: los métodos de Euler

El disco rosa muestra la región de estabilidad del método de Euler.

Considere los métodos de Euler anteriores. El método explícito de Euler aplicado a la ecuación de prueba es ${\displaystyle y'=k\cdot y}$

${\displaystyle y_{n+1}=y_{n}+h\cdot f(t_{n},y_{n})=y_{n}+h\cdot (ky_{n})=y_{n}+h\cdot k\cdot y_{n}=(1+h\cdot k)y_{n}.}$

Por tanto, con . La región de estabilidad absoluta para este método es, por tanto, el disco que se muestra a la derecha. El método de Euler no es A-estable. ${\displaystyle y_{n}=(1+hk)^{n}\cdot y_{0}}$ ${\displaystyle \phi (z)=1+z}$ ${\displaystyle {\bigl \{}z\in \mathbb {C} \,{\big |}\,|1+z|<1{\bigr \}}}$

El ejemplo motivador tenía . El valor de z cuando se toma el tamaño del paso es , que está fuera de la región de estabilidad. De hecho, los resultados numéricos no convergen a cero. Sin embargo, con el tamaño del paso , tenemos que está justo dentro de la región de estabilidad y los resultados numéricos convergen a cero, aunque bastante lentamente. ${\displaystyle k=-15}$ ${\displaystyle h={\tfrac {1}{4}}}$ ${\displaystyle z=-15\times {\tfrac {1}{4}}=-3.75}$ ${\displaystyle h={\tfrac {1}{8}}}$ ${\displaystyle z=-1.875}$

Ejemplo: método trapezoidal

La región rosa es la región de estabilidad del método trapezoidal.

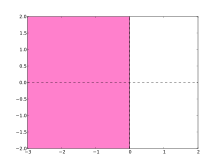
Considere el método trapezoidal.

${\displaystyle y_{n+1}=y_{n}+{\tfrac {1}{2}}h\cdot {\bigl (}f(t_{n},y_{n})+f(t_{n+1},y_{n+1}){\bigr )},}$

cuando se aplica a la ecuación de prueba , es ${\displaystyle y'=k\cdot y}$

${\displaystyle y_{n+1}=y_{n}+{\tfrac {1}{2}}h\cdot \left(ky_{n}+ky_{n+1}\right).}$

Resolviendo para los rendimientos ${\displaystyle y_{n+1}}$

${\displaystyle y_{n+1}={\frac {1+{\frac {1}{2}}hk}{1-{\frac {1}{2}}hk}}\cdot y_{n}.}$

Por tanto, la función de estabilidad es

${\displaystyle \phi (z)={\frac {1+{\frac {1}{2}}z}{1-{\frac {1}{2}}z}}}$

y la región de estabilidad absoluta es

${\displaystyle \left\{z\in \mathbb {C} \ \left|\ \left|{\frac {1+{\frac {1}{2}}z}{1-{\frac {1}{2}}z}}\right|<1\right.\right\}.}$

Esta región contiene el semiplano izquierdo, por lo que el método trapezoidal es A-estable. De hecho, la región de estabilidad es idéntica al semiplano izquierdo y, por tanto, la solución numérica de converge a cero si y sólo si la solución exacta lo hace. Sin embargo, el método trapezoidal no tiene un comportamiento perfecto: amortigua todos los componentes que se descomponen, pero los componentes que se descomponen rápidamente se amortiguan sólo muy suavemente, porque como . Esto llevó al concepto de L-estabilidad : un método es L-estable si es A-estable y como . El método trapezoidal es A-estable pero no L-estable. El método implícito de Euler es un ejemplo de método L-estable. ^[8] ${\displaystyle y'=k\cdot y}$ ${\displaystyle \phi (z)\to 1}$ ${\displaystyle z\to -\infty }$ ${\displaystyle |\phi (z)|\to 0}$ ${\displaystyle z\to \infty }$

teoría general

La función de estabilidad de un método de Runge-Kutta con coeficientes y está dada por ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathbf {b} }$

${\displaystyle \phi (z)={\frac {\det \left(\mathbf {I} -z\mathbf {A} +z\mathbf {e} \mathbf {b} ^{\mathsf {T}}\right)}{\det(\mathbf {I} -z\mathbf {A} )}},}$

donde denota el vector con todos unos. Esta es una función racional (un polinomio dividido por otro). ${\displaystyle \mathbf {e} }$

Los métodos explícitos de Runge-Kutta tienen una matriz de coeficientes triangular estrictamente inferior y, por tanto, su función de estabilidad es un polinomio. De ello se deduce que los métodos explícitos de Runge-Kutta no pueden ser A-estables. ${\displaystyle \mathbf {A} }$

La función de estabilidad de los métodos implícitos de Runge-Kutta a menudo se analiza utilizando estrellas de orden. La estrella de orden para un método con función de estabilidad se define como el conjunto . Un método es A-estable si y sólo si su función de estabilidad no tiene polos en el plano izquierdo y su estrella de orden no contiene números puramente imaginarios. ^[9] ${\displaystyle \phi }$ ${\displaystyle {\bigl \{}z\in \mathbb {C} \,{\big |}\,|\phi (z)|>|e^{z}|{\bigr \}}}$

Métodos de varios pasos

Los métodos lineales de varios pasos tienen la forma

${\displaystyle y_{n+1}=\sum _{i=0}^{s}a_{i}y_{n-i}+h\sum _{j=-1}^{s}b_{j}f\left(t_{n-j},y_{n-j}\right).}$

Aplicados a la ecuación de prueba, se convierten en

${\displaystyle y_{n+1}=\sum _{i=0}^{s}a_{i}y_{n-i}+hk\sum _{j=-1}^{s}b_{j}y_{n-j},}$

que se puede simplificar a

${\displaystyle \left(1-b_{-1}z\right)y_{n+1}-\sum _{j=0}^{s}\left(a_{j}+b_{j}z\right)y_{n-j}=0}$

dónde . Esta es una relación de recurrencia lineal . El método es A-estable si todas las soluciones de la relación de recurrencia convergen a cero cuando . El polinomio característico es ${\displaystyle z=hk}$ ${\displaystyle \{y_{n}\}}$ ${\displaystyle \operatorname {Re} (z)<0}$

${\displaystyle \Phi (z,w)=w^{s+1}-\sum _{i=0}^{s}a_{i}w^{s-i}-z\sum _{j=-1}^{s}b_{j}w^{s-j}.}$

Todas las soluciones convergen a cero para un valor dado de si todas las soluciones de se encuentran en el círculo unitario. ${\displaystyle z}$ ${\displaystyle w}$ ${\displaystyle \Phi (z,w)=0}$

La región de estabilidad absoluta para un método de varios pasos de la forma anterior es entonces el conjunto de todos los que satisfacen . Nuevamente, si este conjunto contiene el semiplano izquierdo, se dice que el método de varios pasos es A-estable. ${\displaystyle z\in \mathbb {C} }$ ${\displaystyle w}$ ${\displaystyle \Phi (z,w)=0}$ ${\displaystyle |w|<1}$

Ejemplo: el método Adams-Bashforth de segundo orden

La región rosa es la región de estabilidad del método Adams-Bashforth de segundo orden.

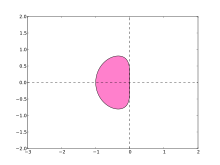
Determinemos la región de estabilidad absoluta para el método de dos pasos Adams-Bashforth

${\displaystyle y_{n+1}=y_{n}+h\left({\tfrac {3}{2}}f(t_{n},y_{n})-{\tfrac {1}{2}}f(t_{n-1},y_{n-1})\right).}$

El polinomio característico es

${\displaystyle \Phi (w,z)=w^{2}-\left(1+{\tfrac {3}{2}}z\right)w+{\tfrac {1}{2}}z=0}$

que tiene raíces

${\displaystyle w={\tfrac {1}{2}}\left(1+{\tfrac {3}{2}}z\pm {\sqrt {1+z+{\tfrac {9}{4}}z^{2}}}\right),}$

por tanto, la región de estabilidad absoluta es

${\displaystyle \left\{z\in \mathbb {C} \ \left|\ \left|{\tfrac {1}{2}}\left(1+{\tfrac {3}{2}}z\pm {\sqrt {1+z+{\tfrac {9}{4}}z^{2}}}\right)\right|<1\right.\right\}.}$

Esta región se muestra a la derecha. No incluye todo el semiplano izquierdo (de hecho, solo incluye el eje real entre ), por lo que el método Adams-Bashforth no es A-estable. ${\displaystyle -1\leq z\leq 0}$

teoría general

Los métodos explícitos de varios pasos nunca pueden ser A-estables, al igual que los métodos explícitos de Runge-Kutta. Los métodos implícitos de varios pasos sólo pueden ser A-estables si su orden es como máximo 2. Este último resultado se conoce como segunda barrera de Dahlquist ; restringe la utilidad de los métodos lineales de varios pasos para ecuaciones rígidas. Un ejemplo de un método A-estable de segundo orden es la regla trapezoidal mencionada anteriormente, que también puede considerarse como un método lineal de varios pasos. ^[10]

Ver también

• Fórmula de diferenciación hacia atrás , una familia de métodos implícitos especialmente utilizados para la solución de ecuaciones diferenciales rígidas.
• Número de condición
• Inclusión diferencial , una extensión de la noción de ecuación diferencial que permite discontinuidades, en parte como una forma de eludir algunos problemas de rigidez.
• Métodos explícitos e implícitos.

Notas

1. Robertson, HH (1966). "La solución de un conjunto de ecuaciones de velocidad de reacción". Análisis numérico: una introducción . Prensa académica. págs. 178–182.
2. Lambert (1992, págs. 216-217)
3. Lambert (1992, págs. 217-220)
4. Hirshfelder (1963)
5. Carga y ferias (1993, pág.314)
6. Kreyszig (1972, págs. 62–68)
7. Esta definición se debe a Dahlquist (1963).
8. La definición de L-estabilidad se debe a Ehle (1969).
9. La definición se debe a Wanner, Hairer & Nørsett (1978); véase también Iserles y Nørsett (1991).
10. Véase Dahlquist (1963).

Referencias

• Carga, Richard L.; Faires, J. Douglas (1993), Análisis numérico (5ª ed.), Boston: Prindle, Weber y Schmidt, ISBN 0-534-93219-3.
• Dahlquist, Germund (1963), "Un problema de estabilidad especial para métodos lineales de varios pasos", BIT , 3 (1): 27–43, doi :10.1007/BF01963532, hdl : 10338.dmlcz/103497 , S2CID  120241743.
• Eberly, David (2008), Análisis de estabilidad para sistemas de ecuaciones diferenciales (PDF).
• Ehle, BL (1969), Sobre las aproximaciones de Padé a la función exponencial y los métodos A-estables para la solución numérica de problemas de valores iniciales (PDF) , Universidad de Waterloo.
• Gear, CW (1971), Problemas numéricos de valores iniciales en ecuaciones diferenciales ordinarias , Englewood Cliffs: Prentice Hall , Bibcode : 1971nivp.book.....G.
• Gear, CW (1981), "Solución numérica de ecuaciones diferenciales ordinarias: ¿Queda algo por hacer?", SIAM Review , 23 (1): 10–24, doi :10.1137/1023002.
• Hairer, Ernst; Wanner, Gerhard (1996), Resolución de ecuaciones diferenciales ordinarias II: problemas rígidos y algebraicos diferenciales (segunda ed.), Berlín: Springer-Verlag , ISBN 978-3-540-60452-5.
• Hirshfelder, JO (1963), "Matemáticas aplicadas utilizadas en química teórica", Simposio de la Sociedad Estadounidense de Matemáticas : 367–376.
• Iserles, Arieh; Nørsett, Syvert (1991), Orden de estrellas , Chapman & Hall , ISBN 978-0-412-35260-7.
• Kreyszig, Erwin (1972), Matemáticas de ingeniería avanzada (3.ª ed.), Nueva York: Wiley , ISBN 0-471-50728-8.
• Lambert, JD (1977), D. Jacobs (ed.), "El problema del valor inicial para ecuaciones diferenciales ordinarias", El estado del arte en análisis numérico , Nueva York: Academic Press : 451–501.
• Lambert, JD (1992), Métodos numéricos para sistemas diferenciales ordinarios , Nueva York: Wiley , ISBN 978-0-471-92990-1.
• Mateo, Juan; Fink, Kurtis (1992), Métodos numéricos utilizando MATLAB.
• Prensa, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Sección 17.5. Conjuntos rígidos de ecuaciones". Recetas numéricas: el arte de la informática científica (3ª ed.). Nueva York: Cambridge University Press. ISBN 978-0-521-88068-8.
• Champine, LF; Gear, CW (1979), "La visión de un usuario sobre la resolución de ecuaciones diferenciales ordinarias rígidas", SIAM Review , 21 (1): 1–17, doi :10.1137/1021001.
• Wanner, Gerhard; Hairer, Ernst; Nørsett, Syvert (1978), "Estrellas de orden y teoría de la estabilidad", BIT , 18 (4): 475–489, doi :10.1007/BF01932026, S2CID  8824105.
• Estabilidad de los métodos de Runge-Kutta [1]

enlaces externos

• Introducción al modelado basado en la física: funciones energéticas y rigidez
• Sistemas rígidos Lawrence F. Shampine y Skip Thompson Scholarpedia , 2(3):2855. doi:10.4249/scholarpedia.2855