Medida de distancia

Definiciones de distancia entre dos objetos o eventos en el universo

Las medidas de distancia se utilizan en la cosmología física para dar una noción natural de la distancia entre dos objetos o eventos en el universo . A menudo se utilizan para vincular alguna cantidad observable (como la luminosidad de un cuásar distante , el corrimiento al rojo de una galaxia distante o el tamaño angular de los picos acústicos en el espectro de potencia del fondo cósmico de microondas (CMB)) a otra cantidad que no es directamente observable, pero que es más conveniente para los cálculos (como las coordenadas comóviles del cuásar, la galaxia, etc.). Las medidas de distancia discutidas aquí se reducen todas a la noción común de distancia euclidiana a bajo corrimiento al rojo.

De acuerdo con nuestra comprensión actual de la cosmología, estas medidas se calculan dentro del contexto de la relatividad general , donde se utiliza la solución de Friedmann–Lemaître–Robertson–Walker para describir el universo.

Descripción general

Existen algunas definiciones diferentes de "distancia" en cosmología, todas asintóticas entre sí para pequeños corrimientos al rojo . Las expresiones para estas distancias son más prácticas cuando se escriben como funciones del corrimiento al rojo , ya que el corrimiento al rojo siempre es el observable. También se pueden escribir como funciones del factor de escala. ${\displaystyle z}$ ${\displaystyle a=1/(1+z).}$

En el resto de este artículo, se supone que la velocidad peculiar es insignificante a menos que se especifique lo contrario.

Primero damos fórmulas para varias medidas de distancia y luego las describimos con más detalle más adelante. Definimos la "distancia de Hubble" como donde es la velocidad de la luz , es el parámetro de Hubble actual y h es la constante de Hubble adimensional , todas las distancias son asintóticas a para z pequeño . $${\displaystyle d_{H}={\frac {c}{H_{0}}}\approx 3000h^{-1}{\text{Mpc}}\approx 9.26\cdot 10^{25}h^{-1}{\text{m}}}$$ ${\displaystyle c}$ ${\displaystyle H_{0}}$ ${\displaystyle z\cdot d_{H}}$

De acuerdo con las ecuaciones de Friedmann , también definimos un parámetro de Hubble adimensional : ^[1] $${\displaystyle E(z)={\frac {H(z)}{H_{0}}}={\sqrt {\Omega _{r}(1+z)^{4}+\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }}}}$$

Aquí, y son valores normalizados de la densidad de energía de radiación actual, la densidad de materia y la " densidad de energía oscura ", respectivamente (esta última representa la constante cosmológica ), y determina la curvatura. El parámetro de Hubble en un corrimiento al rojo dado es entonces . ${\displaystyle \Omega _{r},\Omega _{m},}$ ${\displaystyle \Omega _{\Lambda }}$ ${\displaystyle \Omega _{k}=1-\Omega _{r}-\Omega _{m}-\Omega _{\Lambda }}$ ${\displaystyle H(z)=H_{0}E(z)}$

La fórmula para la distancia comóvil, que sirve como base para la mayoría de las otras fórmulas, implica una integral . Aunque para algunas opciones limitadas de parámetros (ver más abajo) la integral de la distancia comóvil tiene una forma analítica cerrada, en general, y específicamente para los parámetros de nuestro universo , solo podemos encontrar una solución numéricamente . Los cosmólogos usan comúnmente las siguientes medidas para las distancias desde el observador a un objeto en el corrimiento al rojo a lo largo de la línea de visión (LOS): ^[2] ${\displaystyle z}$

• Distancia de comovimiento: $${\displaystyle d_{C}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{E(z')}}}$$
• Distancia comóvil transversal: $${\displaystyle d_{M}(z)={\begin{cases}{\frac {d_{H}}{\sqrt {\Omega _{k}}}}\sinh \left({\frac {{\sqrt {\Omega _{k}}}d_{C}(z)}{d_{H}}}\right)&\Omega _{k}>0\\d_{C}(z)&\Omega _{k}=0\\{\frac {d_{H}}{\sqrt {|\Omega _{k}|}}}\sin \left({\frac {{\sqrt {|\Omega _{k}|}}d_{C}(z)}{d_{H}}}\right)&\Omega _{k}<0\end{cases}}}$$
• Distancia del diámetro angular: $${\displaystyle d_{A}(z)={\frac {d_{M}(z)}{1+z}}}$$
• Distancia de luminosidad: $${\displaystyle d_{L}(z)=(1+z)d_{M}(z)}$$
• Distancia recorrida por la luz: $${\displaystyle d_{T}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{(1+z')E(z')}}}$$

Comparación de medidas de distancia cosmológica, desde un corrimiento al rojo cero hasta un corrimiento al rojo de 0,5. La cosmología de fondo es el parámetro Hubble de 72 km/s/Mpc, , , , y se eligió de modo que la suma de los parámetros Omega sea 1. Edwin Hubble utilizó galaxias hasta un corrimiento al rojo de un poco más de 0,003 ( Messier 60 ). ${\displaystyle \Omega _{\Lambda }=0.732}$ ${\displaystyle \Omega _{\rm {matter}}=0.266}$ ${\displaystyle \Omega _{\rm {radiation}}=0.266/3454}$ ${\displaystyle \Omega _{k}}$

Comparación de las medidas de distancia cosmológica, desde el corrimiento al rojo cero hasta el corrimiento al rojo de 10 000, correspondientes a la época de igualdad materia/radiación. La cosmología de fondo es el parámetro Hubble de 72 km/s/Mpc, , , , y se eligió de modo que la suma de los parámetros Omega sea uno. ${\displaystyle \Omega _{\Lambda }=0.732}$ ${\displaystyle \Omega _{\rm {matter}}=0.266}$ ${\displaystyle \Omega _{\rm {radiation}}=0.266/3454}$ ${\displaystyle \Omega _{k}}$

Terminología alternativa

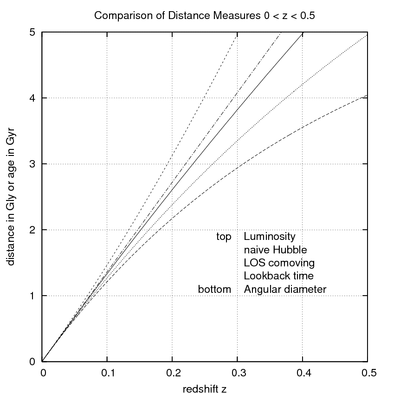
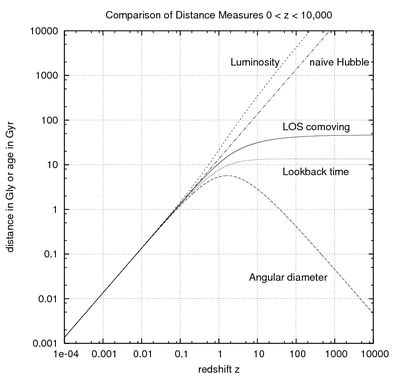
Peebles denomina a la distancia de movimiento transversal "distancia de tamaño angular", que no debe confundirse con la distancia de diámetro angular. ^[1] En ocasiones, se utilizan los símbolos o para indicar tanto la distancia de movimiento transversal como la de diámetro angular. A veces, la distancia recorrida por la luz también se denomina "distancia de retrospección" o "tiempo de retrospección". ^{[ cita requerida ]} ${\displaystyle \chi }$ ${\displaystyle r}$

Detalles

Velocidad peculiar

En observaciones reales, el movimiento de la Tierra con respecto al flujo de Hubble tiene un efecto sobre el corrimiento al rojo observado. ^{[ cita requerida ]}

En realidad, existen dos nociones de corrimiento al rojo. Una es el corrimiento al rojo que se observaría si tanto la Tierra como el objeto no se movieran con respecto a los alrededores "comóviles" (el flujo de Hubble ), definido por el fondo cósmico de microondas. La otra es el corrimiento al rojo real medido, que depende tanto de la velocidad peculiar del objeto observado como de su velocidad peculiar. Dado que el Sistema Solar se mueve a unos 370 km/s en una dirección entre Leo y Crater , esta velocidad disminuye para los objetos distantes en esa dirección en un factor de aproximadamente 1,0012 y aumenta en el mismo factor para los objetos distantes en la dirección opuesta. (La velocidad del movimiento de la Tierra alrededor del Sol es de solo 30 km/s.) ^{[ cita requerida ]} ${\displaystyle 1+z}$

Distancia de comovimiento

La distancia de comorbilidad entre observadores fundamentales, es decir, observadores que se mueven con el flujo de Hubble , no cambia con el tiempo, ya que la distancia de comorbilidad explica la expansión del universo. La distancia de comorbilidad se obtiene integrando las distancias adecuadas de los observadores fundamentales cercanos a lo largo de la línea de visión ( LOS ), mientras que la distancia adecuada es la que obtendría una medición en tiempo cósmico constante. ^{[ cita requerida ]} ${\displaystyle d_{C}}$

En la cosmología estándar , la distancia comomóvil y la distancia propia son dos medidas de distancia estrechamente relacionadas que utilizan los cosmólogos para medir distancias entre objetos; la distancia comomóvil es la distancia propia en el momento actual. ^{[ cita requerida ]}

La distancia comóvil (con una pequeña corrección por nuestro propio movimiento) es la distancia que se obtendría a partir de la paralaje, porque el paralaje en grados es igual a la relación entre una unidad astronómica y la circunferencia de un círculo que en el momento actual pasa por el Sol y tiene como centro el objeto distante, multiplicada por 360°. Sin embargo, los objetos más allá de un megaparsec tienen una paralaje demasiado pequeña para ser medida (el telescopio espacial Gaia mide la paralaje de las estrellas más brillantes con una precisión de 7 microsegundos de arco), por lo que la paralaje de las galaxias fuera de nuestro Grupo Local es demasiado pequeña para ser medida.

Existe una expresión de forma cerrada para la integral en la definición de la distancia comóvil si o, sustituyendo el factor de escala por , si . Nuestro universo ahora parece estar representado de manera precisa por En este caso, tenemos: donde ${\displaystyle \Omega _{r}=\Omega _{m}=0}$ ${\displaystyle a}$ ${\displaystyle 1/(1+z)}$ ${\displaystyle \Omega _{\Lambda }=0}$ ${\displaystyle \Omega _{r}=\Omega _{k}=0.}$ $${\displaystyle d_{C}(z)=d_{H}\Omega _{m}^{-1/3}\Omega _{\Lambda }^{-1/6}[f((1+z)(\Omega _{m}/\Omega _{\Lambda })^{1/3})-f((\Omega _{m}/\Omega _{\Lambda })^{1/3})]}$$ $${\displaystyle f(x)\equiv \int _{0}^{x}{\frac {dx}{\sqrt {x^{3}+1}}}}$$

La distancia de comorbilidad debe calcularse utilizando el valor de z que correspondería si ni el objeto ni nosotros tuviéramos una velocidad peculiar.

Junto con el factor de escala, nos da la distancia adecuada del objeto cuando la luz que vemos ahora fue emitida por él y emprendió su viaje hacia nosotros: $${\displaystyle d=ad_{C}}$$

Distancia adecuada

La distancia propia corresponde aproximadamente a la posición que ocuparía un objeto distante en un momento específico del tiempo cosmológico , que puede cambiar con el tiempo debido a la expansión del universo . La distancia comomóvil excluye la expansión del universo, lo que da una distancia que no cambia con el tiempo debido a la expansión del espacio (aunque puede cambiar debido a otros factores locales, como el movimiento de una galaxia dentro de un cúmulo); la distancia comomóvil es la distancia propia en el momento actual. ^{[ cita requerida ]}

Distancia comóvil transversal

Se dice que dos objetos comóviles con un corrimiento al rojo constante que están separados por un ángulo en el cielo tienen la distancia , donde la distancia comóvil transversal se define apropiadamente. ^{[ cita requerida ]} ${\displaystyle z}$ ${\displaystyle \delta \theta }$ ${\displaystyle \delta \theta d_{M}(z)}$ ${\displaystyle d_{M}}$

Distancia de diámetro angular

Un objeto de tamaño en el desplazamiento al rojo que parece tener un tamaño angular tiene una distancia de diámetro angular de . Esto se utiliza comúnmente para observar las llamadas reglas estándar , por ejemplo, en el contexto de las oscilaciones acústicas bariónicas . ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle \delta \theta }$ ${\displaystyle d_{A}(z)=x/\delta \theta }$

Para tener en cuenta la velocidad peculiar de la Tierra, se debe utilizar el corrimiento al rojo correspondiente en ese caso, pero se debe corregir para el movimiento del sistema solar por un factor entre 0,99867 y 1,00133, dependiendo de la dirección. (Si uno comienza a moverse con velocidad v hacia un objeto, a cualquier distancia, el diámetro angular de ese objeto disminuye en un factor de ) ${\displaystyle d_{A}}$ ${\textstyle {\sqrt {(1+v/c)/(1-v/c)}}.}$

Distancia de luminosidad

Si se conoce la luminosidad intrínseca de un objeto distante, podemos calcular su distancia de luminosidad midiendo el flujo y determinar , que resulta ser equivalente a la expresión anterior para . Esta cantidad es importante para las mediciones de candelas estándar como las supernovas de tipo Ia , que se utilizaron por primera vez para descubrir la aceleración de la expansión del universo . ${\displaystyle L}$ ${\displaystyle S}$ ${\textstyle d_{L}(z)={\sqrt {L/4\pi S}}}$ ${\displaystyle d_{L}(z)}$

Al tener en cuenta la velocidad peculiar de la Tierra, se debe utilizar el corrimiento al rojo correspondiente en ese caso , pero el factor debe utilizar el corrimiento al rojo medido y se debe realizar otra corrección para la velocidad peculiar del objeto multiplicando por donde ahora v es el componente de la velocidad peculiar del objeto que se aleja de nosotros. De esta manera, la distancia de luminosidad será igual a la distancia del diámetro angular multiplicada por donde z es el corrimiento al rojo medido, de acuerdo con el teorema de reciprocidad de Etherington (ver más abajo). ${\displaystyle d_{M},}$ ${\displaystyle (1+z)}$ ${\textstyle {\sqrt {(1+v/c)/(1-v/c)}},}$ ${\displaystyle (1+z)^{2},}$

Distancia recorrida por la luz

(también conocido como "tiempo de retrospección" o "distancia de retrospección") ^[3]

Esta distancia es el tiempo que tarda la luz en llegar al observador desde el objeto multiplicado por la velocidad de la luz . Por ejemplo, el radio del universo observable en esta medida de distancia se convierte en la edad del universo multiplicada por la velocidad de la luz (1 año luz/año), lo que resulta ser aproximadamente 13.800 millones de años luz. ^{[ cita requerida ]} ${\displaystyle d_{T}}$

Existe una solución en forma cerrada de la distancia recorrida por la luz si se involucran las funciones hiperbólicas inversas o (o se involucran las funciones trigonométricas inversas si la constante cosmológica tiene el otro signo). Si entonces existe una solución en forma cerrada para pero no para ${\displaystyle \Omega _{r}=\Omega _{m}=0}$ ${\displaystyle {\text{arcosh}}}$ ${\displaystyle {\text{arsinh}}}$ ${\displaystyle \Omega _{r}=\Omega _{\Lambda }=0}$ ${\displaystyle d_{T}(z)}$ ${\displaystyle z(d_{T}).}$

Nótese que la distancia comomóvil se recupera a partir de la distancia comomóvil transversal tomando el límite , de modo que las dos medidas de distancia son equivalentes en un universo plano . ${\displaystyle \Omega _{k}\to 0}$

Existen sitios web para calcular la distancia recorrida por la luz a partir del corrimiento al rojo. ^{[4] [5] [6] [7]}

La edad del universo entonces se convierte en , y el tiempo transcurrido desde el corrimiento al rojo hasta ahora es: ${\displaystyle \lim _{z\to \infty }d_{T}(z)/c}$ ${\displaystyle z}$ ${\displaystyle t(z)=d_{T}(z)/c.}$

La dualidad de distancia de Etherington

La ecuación de dualidad de distancia de Etherington ^[8] es la relación entre la distancia de luminosidad de las velas estándar y la distancia de diámetro angular. Se expresa de la siguiente manera: ${\displaystyle d_{L}=(1+z)^{2}d_{A}}$

Véase también

• Portal espacial

• Gran Explosión
• Cómo moverse y distancias adecuadas
• Ecuaciones de Friedmann
• Pársec
• Cosmología física
• Escalera de distancia cósmica
• Métrica de Friedmann-Lemaître-Robertson-Walker
• Escala subatómica

Referencias

1. Peebles, PJE (1993). Principios de cosmología física . Princeton University Press . págs. 310–320. Código Bibliográfico :1993ppc..book.....P. ISBN 978-0-691-01933-8.
2. David W. Hogg (2000). "Medidas de distancia en cosmología". arXiv : astro-ph/9905116v4 .
3. Staff (2022). «Calculadora de cosmología». Centro Internacional de Investigación en Radioastronomía . Consultado el 4 de agosto de 2022 .
4. Staff (2015). «Calculadora cosmológica de la UCLA». UCLA . Consultado el 6 de agosto de 2022 .La distancia recorrida por la luz se calculó a partir del valor del corrimiento al rojo utilizando la calculadora cosmológica de la UCLA, con valores de parámetros a partir de 2015: H ₀ = 67,74 y Omega _M = 0,3089 (consulte la Tabla/Planck2015 en " Modelo Lambda-CDM#Parámetros ").
5. Staff (2018). «Calculadora cosmológica de la UCLA». UCLA . Consultado el 6 de agosto de 2022 .La distancia recorrida por la luz se calculó a partir del valor del corrimiento al rojo utilizando la Calculadora Cosmológica de la UCLA, con valores de parámetros a partir de 2018: H ₀ = 67,4 y Omega _M = 0,315 (consulte la Tabla/Planck2018 en " Modelo Lambda-CDM#Parámetros ")
6. Staff (2022). «Calculadora de cosmología ICRAR». Centro Internacional de Investigación en Radioastronomía . Consultado el 6 de agosto de 2022 .Calculadora de cosmología ICRAR: establezca H ₀ = 67,4 y Omega _M = 0,315 (consulte la Tabla/Planck2018 en " Modelo Lambda-CDM#Parámetros ")
7. Kempner, Joshua (2022). «Calculadora de cosmología KEMPNER». Kempner.net . Consultado el 6 de agosto de 2022 .Calculadora de cosmología KEMP: establezca H ₀ = 67,4, Omega _M = 0,315 y Omega _Λ = 0,6847 (consulte la Tabla/Planck2018 en " Modelo Lambda-CDM#Parámetros ")
8. IMH Etherington, “LX. Sobre la definición de distancia en la relatividad general”, Philosophical Magazine, vol. 15, pág. 7 (1933), págs. 761-773.

• Scott Dodelson, Cosmología moderna. Academic Press (2003).

Enlaces externos

• 'La escala de distancias del universo' compara diferentes medidas de distancia cosmológica.
• 'Medidas de distancia en cosmología' explica en detalle cómo calcular las diferentes medidas de distancia en función del modelo mundial y el corrimiento al rojo.
• iCosmos: Calculadora de cosmología (con generación de gráficos) calcula las diferentes medidas de distancia en función del modelo cosmológico y el corrimiento al rojo, y genera gráficos para el modelo desde el corrimiento al rojo de 0 a 20.