Matriz de distancia

En matemáticas , informática y, especialmente , teoría de grafos , una matriz de distancias es una matriz cuadrada (matriz bidimensional) que contiene las distancias , tomadas por pares, entre los elementos de un conjunto. ^[1] Dependiendo de la aplicación involucrada, la distancia que se utiliza para definir esta matriz puede ser o no una métrica . Si hay $N$ elementos, esta matriz tendrá un tamaño $N \times N.$ En aplicaciones de teoría de grafos, los elementos se denominan más a menudo puntos, nodos o vértices.

Matriz de distancia no métrica

En general, una matriz de distancia es una matriz de adyacencia ponderada de algún grafo. En una red , un grafo dirigido con pesos asignados a los arcos, la distancia entre dos nodos de la red se puede definir como el mínimo de las sumas de los pesos en los caminos más cortos que unen los dos nodos (donde el número de pasos en el camino está acotado). ^[2] Esta función de distancia, aunque bien definida, no es una métrica. No es necesario que haya restricciones en los pesos más allá de la necesidad de poder combinarlos y compararlos, por lo que se utilizan pesos negativos en algunas aplicaciones. Dado que los caminos son dirigidos, no se puede garantizar la simetría y, si existen ciclos de peso negativo, la matriz de distancia puede no ser hueca (y en ausencia de un límite en el recuento de pasos, la matriz puede no estar definida).

Se puede obtener una formulación algebraica de lo anterior utilizando el álgebra min-plus . La multiplicación de matrices en este sistema se define de la siguiente manera: Dadas dos matrices $n \times n$ $A = (a ij)$ y $B = (b ij)$ , su producto de distancia $C = (c ij) = A ⭑ B$ se define como una matriz $n \times n$ tal que

c_{ij}=\min _{k=1}^{n}\{a_{ik}+b_{kj}\}.

Tenga en cuenta que los elementos fuera de la diagonal que no están conectados directamente deberán configurarse en infinito o en un valor grande adecuado para que las operaciones de mínimo-más funcionen correctamente. Un cero en estas ubicaciones se interpretará incorrectamente como un borde sin distancia, costo, etc.

Si $W$ es una matriz $n \times n$ que contiene los pesos de las aristas de un grafo , entonces $W k$ (usando este producto de distancias) da las distancias entre vértices usando caminos de longitud como máximo $k$ aristas, y también lo es la matriz de distancias del grafo cuando el límite de conteo de pasos se establece en k . Si no hay bucles de peso negativo, $W n$ dará la matriz de distancias verdadera, sin límite, porque eliminar vértices repetidos de un camino no puede reducir su peso. Por otro lado, si i y j están en un bucle de peso negativo, $W k ij$ disminuirá sin límite a medida que k aumenta.

Un grafo arbitrario $G$ sobre $n$ vértices puede modelarse como un grafo completo ponderado sobre $n$ vértices asignando un peso de uno a cada arista del grafo completo que corresponde a una arista de $G$ e infinito a todas las demás aristas. $W$ para este grafo completo es la matriz de adyacencia de $G$ . La matriz de distancia de $G$ puede calcularse a partir de $W$ como se indicó anteriormente; por el contrario, si se utiliza la multiplicación de matrices normal y los vértices no vinculados se representan con 0, $W n$ codificaría en cambio el número de caminos entre dos vértices cualesquiera de longitud exactamente $n$ .

Matriz de distancia métrica

El valor de un formalismo de matriz de distancia en muchas aplicaciones radica en cómo la matriz de distancia puede codificar manifiestamente los axiomas métricos y en cómo se presta al uso de técnicas de álgebra lineal. Es decir, si $M = (x ij)$ con $1 \leq i, j \leq N$ es una matriz de distancia para una distancia métrica, entonces

las entradas en la diagonal principal son todas cero (es decir, la matriz es una matriz hueca ), es decir $x ii = 0$ para todo $1 \leq i \leq N$ ,
todas las entradas fuera de la diagonal son positivas ( $x ij > 0$ si $i \neq j$ ), (es decir, una matriz no negativa ),
La matriz es una matriz simétrica ( $x ij = x ji$ ), y
Para cualquier $i$ y $j$ , $x ij \leq x ik + x kj$ para todo $k$ (la desigualdad triangular). Esto se puede expresar en términos de multiplicación de matrices tropicales .

Cuando una matriz de distancias satisface los tres primeros axiomas (lo que la convierte en una semimétrica), a veces se la denomina matriz de predisposición. Una matriz de predisposición que se puede incluir en un espacio euclidiano se denomina matriz de distancias euclidianas . Para los datos de tipo mixto que contienen descriptores numéricos y categóricos, la distancia de Gower es una alternativa común.

Otro ejemplo común de una matriz de distancia métrica surge en la teoría de codificación cuando en un código de bloques los elementos son cadenas de longitud fija a lo largo de un alfabeto y la distancia entre ellos está dada por la métrica de distancia de Hamming . La entrada más pequeña distinta de cero en la matriz de distancia mide la capacidad de corrección y detección de errores del código.

Matriz de distancia aditiva

Una matriz de distancia aditiva es un tipo especial de matriz que se utiliza en bioinformática para construir un árbol filogenético . Sea $x$ el ancestro común más bajo entre dos especies $i$ y $j$ , esperamos que $M ij = M ix + M xj$ . De aquí proviene la métrica aditiva. Se dice que una matriz de distancia $M$ para un conjunto de especies $S$ es aditiva si y solo si existe una filogenia $T$ para $S$ tal que:

Cada arista $(u, v)$ en $T$ está asociada con un peso positivo $d uv$
Para cada $i, j \in S$ , $M ij$ es igual a la suma de los pesos a lo largo del camino de $i$ a $j$ en $T$

Para este caso, $M$ se denomina matriz aditiva y $T$ árbol aditivo. A continuación podemos ver un ejemplo de matriz de distancias aditivas y su árbol correspondiente:

Matriz de distancia ultramétrica

La matriz de distancia ultramétrica se define como una matriz aditiva que modela el reloj molecular constante . Se utiliza para construir un árbol filogenético. Se dice que una matriz $M$ es ultramétrica si existe un árbol $T$ tal que:

$M ij$ es igual a la suma de los pesos de los bordes a lo largo de la ruta de $i$ a $j$ en $T$
La raíz de un árbol se puede identificar porque la distancia a todas sus hojas es la misma.

A continuación se muestra un ejemplo de una matriz de distancia ultramétrica con su árbol correspondiente:

Bioinformática

La matriz de distancias se utiliza ampliamente en el campo de la bioinformática y está presente en varios métodos, algoritmos y programas. Las matrices de distancias se utilizan para representar estructuras de proteínas de manera independiente de las coordenadas, así como las distancias por pares entre dos secuencias en el espacio de secuencias . Se utilizan en el alineamiento estructural y secuencial , y para la determinación de estructuras de proteínas a partir de RMN o cristalografía de rayos X.

A veces es más conveniente expresar los datos como una matriz de similitud .

También se utiliza para definir la correlación de distancia .

Alineación de secuencias

Una alineación de dos secuencias se forma insertando espacios en ubicaciones arbitrarias a lo largo de las secuencias de modo que terminen con la misma longitud y no haya dos espacios en la misma posición de las dos secuencias aumentadas. ^[3] Uno de los métodos principales para la alineación de secuencias es la programación dinámica . El método se utiliza para llenar la matriz de distancia y luego obtener la alineación. En el uso típico, para la alineación de secuencias se utiliza una matriz para asignar puntajes a las coincidencias o desajustes de aminoácidos, y una penalización por brecha para la coincidencia de un aminoácido en una secuencia con una brecha en la otra.

Alineación global

El algoritmo Needleman-Wunsch utilizado para calcular la alineación global utiliza programación dinámica para obtener la matriz de distancias.

Alineación local

El algoritmo Smith-Waterman también se basa en programación dinámica y consiste también en obtener la matriz de distancias y luego obtener la alineación local.

Alineación de secuencias múltiples

La alineación de secuencias múltiples es una extensión de la alineación por pares para alinear varias secuencias a la vez. Los distintos métodos de MSA se basan en la misma idea de la matriz de distancias que las alineaciones globales y locales.

Método de la estrella central. Este método define una secuencia central $S c$ que minimiza la distancia entre la secuencia $S c$ y cualquier otra secuencia $S i$ . Luego genera un alineamiento múltiple $M$ para el conjunto de secuencias $S$ de modo que para cada $S i$ la distancia de alineamiento $d M (S c, S i)$ sea el alineamiento por pares óptimo. Este método tiene la característica de que el alineamiento calculado para $S$ cuya distancia de suma de pares es como máximo el doble del alineamiento múltiple óptimo.
Método de alineación progresiva. Este método heurístico para crear MSA alinea primero las dos secuencias más relacionadas y luego alinea progresivamente las dos secuencias siguientes más relacionadas hasta que todas las secuencias estén alineadas.

Existen otros métodos que tienen su propio programa debido a su popularidad:

ClustalW
MÚSCULO
MAFFT
MANGO
Y muchos más

MAFFT

El alineamiento múltiple mediante la transformada rápida de Fourier (MAFFT) es un programa con un algoritmo basado en el alineamiento progresivo y ofrece varias estrategias de alineamiento múltiple. En primer lugar, MAFFT construye una matriz de distancias basada en el número de 6-tuplas compartidas. En segundo lugar, construye el árbol guía basándose en la matriz anterior. En tercer lugar, agrupa las secuencias con la ayuda de la transformada rápida de Fourier e inicia el alineamiento. En función del nuevo alineamiento, reconstruye el árbol guía y vuelve a alinear.

Análisis filogenético

Para realizar un análisis filogenético , el primer paso es reconstruir el árbol filogenético: dada una colección de especies, el problema es reconstruir o inferir las relaciones ancestrales entre las especies, es decir, el árbol filogenético entre las especies. Los métodos de matriz de distancias realizan esta actividad.

Métodos de matriz de distancia

Los métodos de análisis filogenético basados en matrices de distancias se basan explícitamente en una medida de "distancia genética" entre las secuencias que se están clasificando y, por lo tanto, requieren múltiples secuencias como entrada. Los métodos de distancia intentan construir una matriz de todos a todos a partir del conjunto de consultas de secuencias que describe la distancia entre cada par de secuencias. A partir de esto, se construye un árbol filogenético que coloca secuencias estrechamente relacionadas bajo el mismo nodo interior y cuyas longitudes de rama reproducen de manera cercana las distancias observadas entre secuencias. Los métodos de matriz de distancias pueden producir árboles con o sin raíz, según el algoritmo utilizado para calcularlos. ^[4] Dadas $n$ especies, la entrada es una matriz de distancias $n \times n$ $M$ donde $M ij$ es la distancia de mutación entre las especies $i$ y $j$ . El objetivo es generar un árbol de grado $3$ que sea consistente con la matriz de distancias.

Se utilizan con frecuencia como base para tipos progresivos e iterativos de alineamiento de secuencias múltiples . La principal desventaja de los métodos de matriz de distancia es su incapacidad para utilizar de manera eficiente la información sobre regiones locales de alta variación que aparecen en múltiples subárboles. ^[4] A pesar de los problemas potenciales, los métodos de distancia son extremadamente rápidos y a menudo producen una estimación razonable de la filogenia. También tienen ciertos beneficios sobre los métodos que utilizan caracteres directamente. En particular, los métodos de distancia permiten el uso de datos que pueden no convertirse fácilmente en datos de caracteres, como los ensayos de hibridación ADN-ADN .

Los siguientes son métodos basados en la distancia para la reconstrucción de la filogenia:

Reconstrucción aditiva de árboles
UPGMA
Vecino uniéndose
Fitch-Margoliash

Reconstrucción aditiva de árboles

La reconstrucción aditiva de árboles se basa en matrices de distancias aditivas y ultramétricas. Estas matrices tienen una característica especial:

Consideremos una matriz aditiva $M$ . Para tres especies cualesquiera $i, j, k,$ el árbol correspondiente es único. ^[3] Toda matriz de distancia ultramétrica es una matriz aditiva. Podemos observar esta propiedad para el árbol que se muestra a continuación, que consta de las especies $i, j, k$ .

La técnica de reconstrucción de árboles aditivos comienza con este árbol y luego agrega una especie más cada vez, en función de la matriz de distancia combinada con la propiedad mencionada anteriormente. Por ejemplo, considere una matriz aditiva $M$ y 5 especies $a, b, c, d$ y $e$ . Primero formamos un árbol aditivo para dos especies $a$ y $b$ . Luego elegimos una tercera, digamos $c$ y la unimos a un punto $x$ en el borde entre $a$ y $b$ . Los pesos de los bordes se calculan con la propiedad anterior. A continuación, agregamos la cuarta especie $d$ a cualquiera de los bordes. Si aplicamos la propiedad, entonces identificamos que $d$ debe unirse solo a un borde específico. Finalmente, agregamos $e$ siguiendo el mismo procedimiento que antes.

UPGMA

El principio básico de UPGMA (Unweighted Pair Group Method with Arithmetic Mean) es que las especies similares deberían estar más cerca en el árbol filogenético. Por lo tanto, construye el árbol agrupando secuencias similares de forma iterativa. El método funciona construyendo el árbol filogenético de abajo hacia arriba a partir de sus hojas. Inicialmente, tenemos $n$ hojas (o $n$ árboles singleton), cada una representando una especie en $S$ . Esas $n$ hojas se denominan $n$ clústeres. Luego, realizamos $n -1$ iteraciones. En cada iteración, identificamos dos clústeres $C 1$ y $C 2$ con la distancia promedio más pequeña y los fusionamos para formar un clúster más grande $C$ . Si suponemos que $M$ es ultramétrico, para cualquier clúster $C$ creado por el algoritmo UPGMA, $C$ es un árbol ultramétrico válido.

Vecino uniéndose

Neighbor es un método de agrupamiento ascendente. Toma una matriz de distancia que especifica la distancia entre cada par de secuencias. El algoritmo comienza con un árbol completamente sin resolver, cuya topología corresponde a la de una red en estrella , y repite los siguientes pasos hasta que el árbol se resuelve por completo y se conocen todas las longitudes de las ramas:

Basándose en la matriz de distancia actual, calcule la matriz (definida a continuación).
Encuentre el par de taxones distintos i y j (es decir, con) para el cual tiene su valor más bajo. Estos taxones se unen a un nodo recién creado, que está conectado al nodo central.
Calcula la distancia desde cada uno de los taxones del par hasta este nuevo nodo.
Calcula la distancia desde cada uno de los taxones fuera de este par hasta el nuevo nodo.
Inicie nuevamente el algoritmo, reemplazando el par de vecinos unidos con el nuevo nodo y utilizando las distancias calculadas en el paso anterior. ^[5]

Fitch-Margoliash

El método Fitch-Margoliash utiliza un método de mínimos cuadrados ponderados para la agrupación en función de la distancia genética. Las secuencias estrechamente relacionadas reciben más peso en el proceso de construcción del árbol para corregir la mayor inexactitud en la medición de distancias entre secuencias distantemente relacionadas. El criterio de mínimos cuadrados aplicado a estas distancias es más preciso pero menos eficiente que los métodos de unión de vecinos. También se puede aplicar una mejora adicional que corrige las correlaciones entre distancias que surgen de muchas secuencias estrechamente relacionadas en el conjunto de datos, con un mayor costo computacional. ^[6]

Minería de datos y aprendizaje automático

Minería de datos

Una función común en la minería de datos es aplicar el análisis de conglomerados a un conjunto determinado de datos para agruparlos en función de su similitud o mayor similitud con respecto a otros grupos. Las matrices de distancias se volvieron muy dependientes y se utilizaron en el análisis de conglomerados, ya que la similitud se puede medir con una métrica de distancia. Por lo tanto, la matriz de distancias se convirtió en la representación de la medida de similitud entre todos los diferentes pares de datos del conjunto.

Agrupamiento jerárquico

Una matriz de distancias es necesaria para los algoritmos de agrupamiento jerárquico tradicionales , que suelen ser métodos heurísticos empleados en las ciencias biológicas, como la reconstrucción de la filogenia. Al implementar cualquiera de los algoritmos de agrupamiento jerárquico en la minería de datos, la matriz de distancias contendrá todas las distancias por pares entre cada punto y luego comenzará a crear grupos entre dos puntos diferentes o grupos basados completamente en las distancias de la matriz de distancias.

Si N es el número de puntos, la complejidad de la agrupación jerárquica es:

La complejidad temporal se debe a los cálculos repetitivos que se realizan después de cada grupo para actualizar la matriz de distancia. $O(N^{3})$
La complejidad espacial es $O(N^{2})$

Aprendizaje automático

Las métricas de distancia son una parte clave de varios algoritmos de aprendizaje automático, que se utilizan tanto en el aprendizaje supervisado como en el no supervisado . Generalmente se utilizan para calcular la similitud entre puntos de datos: aquí es donde la matriz de distancia es un elemento esencial. El uso de una matriz de distancia efectiva mejora el rendimiento del modelo de aprendizaje automático, ya sea para tareas de clasificación o de agrupamiento. ^[7]

K-Vecinos más cercanos

En el algoritmo k-NN, que es uno de los algoritmos de aprendizaje automático basados en instancias más lentos, pero más simples y más utilizados, se utiliza una matriz de distancia , que se puede utilizar tanto en tareas de clasificación como de regresión. Es uno de los algoritmos de aprendizaje automático más lentos, ya que el resultado previsto de cada muestra de prueba requiere una matriz de distancia completamente calculada entre la muestra de prueba y cada muestra de entrenamiento en el conjunto de entrenamiento. Una vez calculada la matriz de distancia, el algoritmo selecciona la cantidad K de muestras de entrenamiento que están más cerca de la muestra de prueba para predecir el resultado de la muestra de prueba en función del valor mayoritario (clasificación) o promedio (regresión) del conjunto seleccionado.

La complejidad del tiempo de predicción es , para calcular la distancia entre cada muestra de prueba con cada muestra de entrenamiento para construir la matriz de distancia donde: $O(k*n*d)$

k = número de vecinos más cercanos seleccionados
n = tamaño del conjunto de entrenamiento
d = número de dimensiones que se utilizan para los datos

Este modelo centrado en la clasificación predice la etiqueta del objetivo basándose en la matriz de distancia entre el objetivo y cada una de las muestras de entrenamiento para determinar el número K de muestras que están más cerca del objetivo.

Visión por computadora

Se puede utilizar una matriz de distancia en redes neuronales para la regresión 2D a 3D en modelos de aprendizaje automático de predicción de imágenes.

Recuperación de información

Matrices de distancia que utilizan la distancia de mezcla gaussiana

[1]* Distancia de mezcla gaussiana para realizar una búsqueda precisa del vecino más cercano para la recuperación de información. Según un modelo de mezcla finita gaussiana establecido para la distribución de los datos en la base de datos, la distancia de mezcla gaussiana se formula en función de la minimización de la divergencia de Kullback-Leibler entre la distribución de los datos de recuperación y los datos en la base de datos. En la comparación del rendimiento de la distancia de mezcla gaussiana con las conocidas distancias euclidiana y de Mahalanobis en función de una medición de rendimiento de precisión, los resultados experimentales demuestran que la función de distancia de mezcla gaussiana es superior a las demás para diferentes tipos de datos de prueba.

Los algoritmos básicos potenciales que vale la pena mencionar sobre el tema de la recuperación de información son el algoritmo de búsqueda de bancos de peces , una recuperación de información que utiliza matrices de distancia para recopilar el comportamiento colectivo de los bancos de peces. Mediante el uso de un operador de alimentación para actualizar sus pesos

Ecuación A:

x_{i}(t+1)=x_{i}(t)-step_{vol}rand(0,1){\frac {x_{i}(t)-B(t)}{distance(x_{i}(t),B(t))}},

Ecuación B:

x_{i}(t+1)=x_{i}(t)+step_{vol}rand(0,1){\frac {x_{i}(t)-B(t)}{distance(x_{i}(t),B(t))}},

Stepvol define el tamaño del desplazamiento de volumen máximo realizado con la matriz de distancia, específicamente utilizando una matriz de distancia euclidiana .

Evaluación de la similitud o disimilitud de las matrices de similitud de coseno y de distancia

Fórmula de conversión entre la semejanza del coseno y la distancia euclidiana

[2]* Si bien la medida de similitud del coseno es quizás la medida de proximidad aplicada con más frecuencia en la recuperación de información al medir los ángulos entre documentos en el espacio de búsqueda sobre la base del coseno, la distancia euclidiana es invariante a la corrección de la media. La distribución de muestreo de una media se genera mediante el muestreo repetido de la misma población y el registro de las medias de muestra obtenidas. Esto forma una distribución de diferentes medias, y esta distribución tiene su propia media y varianza. Para los datos que pueden ser tanto negativos como positivos, la distribución nula para la similitud del coseno es la distribución del producto escalar de dos vectores unitarios aleatorios independientes. Esta distribución tiene una media de cero y una varianza de 1/n. Mientras que la distancia euclidiana será invariante a esta corrección.

Agrupamiento de documentos

La implementación de una agrupación jerárquica con métricas basadas en la distancia para organizar y agrupar documentos similares requerirá la necesidad y el uso de una matriz de distancia. La matriz de distancia representará el grado de asociación que tiene un documento con otro documento que se utilizará para crear grupos de documentos estrechamente asociados que se utilizarán en métodos de recuperación de documentos relevantes para la consulta de un usuario.

Isomap

Isomap incorpora matrices de distancia para utilizar distancias geodésicas y poder calcular incrustaciones de menor dimensión. Esto ayuda a abordar una colección de documentos que residen en una gran cantidad de dimensiones y permite realizar agrupaciones de documentos.

Visualizador de recuperación de vecindarios (NeRV)

Un algoritmo utilizado tanto para visualización supervisada como no supervisada que utiliza matrices de distancia para encontrar datos similares basándose en las similitudes que se muestran en una pantalla.

La matriz de distancia necesaria para NeRV no supervisado se puede calcular a través de distancias por pares de entradas fijas.

La matriz de distancia necesaria para NeRV supervisado requiere la formulación de una métrica de distancia supervisada para poder calcular la distancia de la entrada de manera supervisada.

Química

La matriz de distancias es un objeto matemático ampliamente utilizado tanto en versiones gráfico-teóricas (topológicas) como geométricas (topográficas) de la química. ^[8] La matriz de distancias se utiliza en química tanto en forma explícita como implícita.

Mecanismos de interconversión entre dos isómeros permutacionales

Se utilizaron matrices de distancia como enfoque principal para representar y revelar la secuencia de ruta más corta necesaria para determinar el reordenamiento entre los dos isómeros permutacionales.

Polinomios de distancia y espectros de distancia

Se requiere el uso explícito de matrices de distancia para construir los polinomios de distancia y los espectros de distancia de las estructuras moleculares.

Modelo de estructura-propiedad

El uso implícito de matrices de distancia se aplicó mediante el uso del número de Weiner / índice de Weiner , una métrica basada en la distancia , que se formuló para representar las distancias en todas las estructuras químicas. El número de Weiner es igual a la mitad de la suma de los elementos de la matriz de distancia.

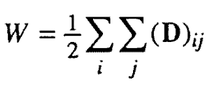
Fórmula de conversión entre el número de Weiner y la matriz de distancias

Matriz de distancias grafo-teórica

Matrices de distancia en química que se utilizan para la realización en 2-D de gráficos moleculares, que se utilizan para ilustrar las principales características fundamentales de una molécula en una gran variedad de aplicaciones.

Creación de un árbol de etiquetas que represente el esqueleto de carbono de una molécula en función de su matriz de distancias. La matriz de distancias es imprescindible en esta aplicación porque las moléculas similares pueden tener una gran variedad de variantes de árboles de etiquetas de su esqueleto de carbono . La estructura de árbol etiquetado del esqueleto de carbono del hexano (C ₆ H ₁₄ ) que se crea en función de la matriz de distancias en el ejemplo tiene diferentes variantes del esqueleto de carbono que afectan tanto a la matriz de distancias como al árbol etiquetado.
Creación de un gráfico etiquetado con pesos de arista, utilizado en la teoría de grafos químicos , que representa moléculas con heteroátomos.
El método Le Verrier-Fadeev-Frame (LVFF) es un método orientado a la computación que se utiliza para acelerar el proceso de detección del centro del grafo en grafos policíclicos. Sin embargo, LVFF requiere que la entrada sea una matriz de distancia diagonalizada que se resuelve fácilmente implementando el algoritmo QL tridiagonal de Householder que toma una matriz de distancia y devuelve la distancia diagonalizada necesaria para el método LVFF.

Matriz de distancia geométrica

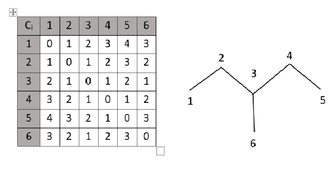
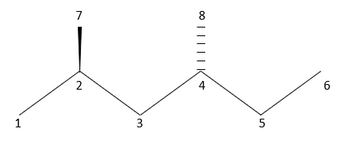
Mientras que la matriz de distancias grafo-teóricas 2-D captura las características constitucionales de la molécula, su carácter tridimensional (3D) está codificado en la matriz de distancias geométricas. La matriz de distancias geométricas es un tipo diferente de matriz de distancias que se basa en la matriz de distancias grafo-teóricas de una molécula para representar y graficar la estructura molecular 3-D. ^[8] La matriz de distancias geométricas de una estructura molecular $G es una matriz$ $n x n$ simétrica real definida de la misma manera que una matriz 2-D. Sin embargo, los elementos de la matriz $D ij$ contendrán una colección de distancias cartesianas más cortas entre $i$ y $j$ en $G$ . También conocida como matriz topográfica, la matriz de distancias geométricas se puede construir a partir de la geometría conocida de la molécula. Como ejemplo, la matriz de distancias geométricas del esqueleto carbonado del 2,4-dimetilhexano se muestra a continuación:

Otras aplicaciones

Análisis de series temporales

Las matrices de distancia de deformación temporal dinámica se utilizan con los algoritmos de agrupamiento y clasificación de una colección/grupo de objetos de series temporales.

Ejemplos

Por ejemplo, supongamos que se van a analizar estos datos, donde la distancia euclidiana del píxel es la métrica de distancia .

La matriz de distancias sería:

Estos datos pueden visualizarse en forma gráfica como un mapa de calor . En esta imagen, el negro indica una distancia de 0 y el blanco es la distancia máxima.

Vista gráfica

Véase también

Referencias

^ Weyenberg, G., y Yoshida, R. (2015). Reconstrucción de la filogenia: métodos computacionales. En Métodos matemáticos discretos y algebraicos para la biología moderna (pp. 293–319). Academic Press.
^ Frank Harary , Robert Z. Norman y Dorwin Cartwright (1965) Modelos estructurales: una introducción a la teoría de grafos dirigidos , páginas 134-138, John Wiley & Sons MR 0184874
^ ab Sung, Wing-Kin (2010). Algoritmos en bioinformática: una introducción práctica . Chapman & Hall. pág. 29. ISBN 978-1-4200-7033-0.
^ ab Felsenstein, José (2003). Inferir filogenias . Asociados Sinauer. ISBN 9780878931774.
^ Saitou, Naruya (1987). "El método de unión de vecinos: un nuevo método para reconstruir árboles filogenéticos". Biología molecular y evolución . 4 (4): 406–425. doi : 10.1093/oxfordjournals.molbev.a040454 . PMID 3447015.
^ Fitch, Walter M. (1967). "Construcción de árboles filogenéticos: un método basado en distancias de mutación estimadas a partir de secuencias de citocromo c es de aplicación general". Science . 155 (3760): 279–284. doi :10.1126/science.155.3760.279. PMID 5334057.
^ "4 tipos de métricas de distancia en el aprendizaje automático". 25 de febrero de 2020.
^ ab Mihalic, Zlatko (1992). "La matriz de distancias en química". Journal of Mathematical Chemistry . 11 : 223–258. doi :10.1007/BF01164206. S2CID 121181446.