
En física y ciencia de los materiales , la plasticidad (también conocida como deformación plástica ) es la capacidad de un material sólido de sufrir una deformación permanente , un cambio de forma no reversible en respuesta a fuerzas aplicadas. [1] [2] Por ejemplo, una pieza sólida de metal que se dobla o golpea para darle una nueva forma muestra plasticidad, ya que se producen cambios permanentes dentro del propio material. En ingeniería, la transición del comportamiento elástico al comportamiento plástico se conoce como fluencia .
La deformación plástica se observa en la mayoría de los materiales, particularmente metales , suelos , rocas , hormigón y espumas . [3] [4] [5] [6] Sin embargo, los mecanismos físicos que causan la deformación plástica pueden variar ampliamente. A escala cristalina , la plasticidad en los metales suele ser una consecuencia de dislocaciones . Dichos defectos son relativamente raros en la mayoría de los materiales cristalinos, pero son numerosos en algunos y parte de su estructura cristalina; en tales casos, puede resultar en cristalinidad plástica . En materiales frágiles como roca, hormigón y hueso, la plasticidad es causada predominantemente por deslizamiento en microfisuras . En materiales celulares como espumas líquidas o tejidos biológicos , la plasticidad es principalmente una consecuencia de reordenamientos de burbujas o células, en particular procesos T1 .
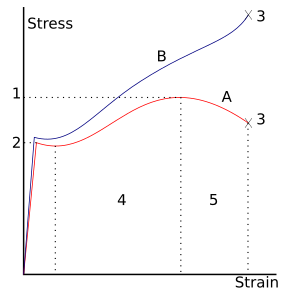
En el caso de muchos metales dúctiles , la carga de tracción aplicada a una muestra hará que esta se comporte de manera elástica. Cada incremento de la carga va acompañado de un incremento proporcional de la extensión. Cuando se retira la carga, la pieza vuelve a su tamaño original. Sin embargo, una vez que la carga supera un umbral (la resistencia a la fluencia), la extensión aumenta más rápidamente que en la región elástica; ahora, cuando se retira la carga, permanecerá cierto grado de extensión.
La deformación elástica , sin embargo, es una aproximación y su calidad depende del marco temporal considerado y de la velocidad de carga. Si, como se indica en el gráfico de la derecha, la deformación incluye una deformación elástica, también se suele denominar "deformación elasto-plástica" o "deformación elasto-plástica".
La plasticidad perfecta es una propiedad de los materiales de sufrir una deformación irreversible sin ningún aumento de tensiones o cargas. Los materiales plásticos que se han endurecido mediante una deformación previa, como el conformado en frío , pueden necesitar tensiones cada vez mayores para deformarse aún más. Generalmente, la deformación plástica también depende de la velocidad de deformación, es decir, normalmente se deben aplicar tensiones mayores para aumentar la velocidad de deformación. Se dice que estos materiales se deforman viscoplásticamente .
La plasticidad de un material es directamente proporcional a la ductilidad y maleabilidad del material.

La plasticidad en un cristal de metal puro se debe principalmente a dos modos de deformación en la red cristalina: deslizamiento y maclado. El deslizamiento es una deformación por cizallamiento que desplaza los átomos a través de muchas distancias interatómicas con respecto a sus posiciones iniciales. El maclado es la deformación plástica que se produce a lo largo de dos planos debido a un conjunto de fuerzas aplicadas a una pieza de metal determinada.
La mayoría de los metales muestran más plasticidad cuando están calientes que cuando están fríos. El plomo muestra suficiente plasticidad a temperatura ambiente, mientras que el hierro fundido no posee suficiente plasticidad para ninguna operación de forjado, incluso cuando está caliente. Esta propiedad es importante en las operaciones de conformado, modelado y extrusión de metales. La mayoría de los metales se vuelven plásticos mediante el calentamiento y, por lo tanto, se moldean en caliente.
Los materiales cristalinos contienen planos uniformes de átomos organizados con un orden de largo alcance. Los planos pueden deslizarse unos sobre otros a lo largo de sus direcciones de empaquetamiento, como se muestra en la página de sistemas de deslizamiento. El resultado es un cambio permanente de forma dentro del cristal y una deformación plástica. La presencia de dislocaciones aumenta la probabilidad de que existan planos.
A escala nanométrica, la deformación plástica primaria en metales cúbicos simples centrados en las caras es reversible, siempre que no haya transporte de material en forma de deslizamiento cruzado . [7] Las aleaciones con memoria de forma, como el alambre de Nitinol, también exhiben una forma reversible de plasticidad que se denomina más apropiadamente pseudoelasticidad .
La presencia de otros defectos dentro de un cristal puede enredar dislocaciones o impedir de algún modo que se deslice. Cuando esto sucede, la plasticidad se localiza en regiones particulares del material. En el caso de los cristales, estas regiones de plasticidad localizada se denominan bandas de cizallamiento .
La microplasticidad es un fenómeno local en los metales. Se produce en valores de tensión en los que el metal se encuentra globalmente en el dominio elástico , mientras que algunas áreas locales se encuentran en el dominio plástico. [8]
En los materiales amorfos , la discusión de las "dislocaciones" no es aplicable, ya que el material entero carece de un orden de largo alcance. Estos materiales aún pueden sufrir deformación plástica. Dado que los materiales amorfos, como los polímeros, no están bien ordenados, contienen una gran cantidad de volumen libre o espacio desperdiciado. Tirar de estos materiales en tensión abre estas regiones y puede dar a los materiales una apariencia borrosa. Esta turbidez es el resultado del agrietamiento , donde se forman fibrillas dentro del material en regiones de alta tensión hidrostática . El material puede pasar de una apariencia ordenada a un patrón "loco" de tensión y estrías.
Estos materiales se deforman plásticamente cuando el momento de flexión supera el momento totalmente plástico. Esto se aplica a las espumas de celdas abiertas donde el momento de flexión se ejerce sobre las paredes de las celdas. Las espumas pueden estar hechas de cualquier material con un límite elástico plástico, lo que incluye polímeros rígidos y metales. Este método de modelar la espuma como vigas solo es válido si la relación entre la densidad de la espuma y la densidad de la materia es menor de 0,3. Esto se debe a que las vigas ceden axialmente en lugar de doblarse. En las espumas de celdas cerradas, la resistencia a la fluencia aumenta si el material está bajo tensión debido a la membrana que se extiende por la cara de las celdas.
Los suelos, en particular las arcillas, presentan una cantidad significativa de inelasticidad bajo carga. Las causas de la plasticidad en los suelos pueden ser bastante complejas y dependen en gran medida de la microestructura , la composición química y el contenido de agua. El comportamiento plástico en los suelos se debe principalmente a la reorganización de los grupos de granos adyacentes.
Las deformaciones inelásticas de las rocas y del hormigón se deben principalmente a la formación de microfisuras y a los movimientos de deslizamiento en relación con dichas fisuras. A altas temperaturas y presiones, el comportamiento plástico también puede verse afectado por el movimiento de las dislocaciones en los granos individuales de la microestructura.
[9]
El flujo plástico independiente del tiempo tanto en monocristales como en policristales se define mediante una tensión cortante resuelta crítica/máxima ( τ CRSS ), que inicia la migración de dislocaciones a lo largo de planos de deslizamiento paralelos de un sistema de deslizamiento único, definiendo así la transición del comportamiento de deformación elástica al comportamiento de deformación plástica en materiales cristalinos.
La tensión de corte crítica resuelta para monocristales se define mediante la ley de Schmid τ CRSS = σ y /m, donde σ y es la resistencia a la fluencia del monocristal y m es el factor de Schmid. El factor de Schmid comprende dos variables λ y φ, que definen el ángulo entre la dirección del plano de deslizamiento y la fuerza de tracción aplicada, y el ángulo entre la normal del plano de deslizamiento y la fuerza de tracción aplicada, respectivamente. En particular, debido a que m > 1, σ y > τ CRSS .
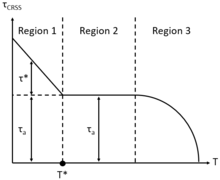
Existen tres regiones características de la tensión cortante crítica resuelta en función de la temperatura. En la región de baja temperatura 1 ( T ≤ 0,25 T m ), la tasa de deformación debe ser alta para lograr un τ CRSS alto que se requiere para iniciar el deslizamiento de las dislocaciones y el flujo plástico equivalente. En la región 1, la tensión cortante crítica resuelta tiene dos componentes: tensiones cortantes atérmicas ( τ a ) y térmicas ( τ *), que surgen de la tensión requerida para mover las dislocaciones en presencia de otras dislocaciones, y la resistencia de los obstáculos de defectos puntuales a la migración de las dislocaciones, respectivamente. En T = T *, se define la región de temperatura moderada 2 (0,25 T m < T < 0,7 T m ), donde el componente de tensión cortante térmica τ * → 0, que representa la eliminación de la impedancia de los defectos puntuales a la migración de las dislocaciones. Por lo tanto, la tensión cortante crítica resuelta independiente de la temperatura τ CRSS = τ a permanece así hasta que se define la región 3. En particular, en la región 2 se deben considerar mecanismos de deformación plástica dependientes del tiempo y de temperatura moderada (fluencia), como el arrastre de soluto. Además, en la región de alta temperatura 3 ( T ≥ 0,7 T m ) έ puede ser baja, lo que contribuye a un bajo τ CRSS , sin embargo, aún se producirá flujo plástico debido a mecanismos de deformación plástica dependientes del tiempo y de alta temperatura activados térmicamente, como el flujo difusional de Nabarro-Herring (NH) y Coble a través de la red y a lo largo de las superficies del monocristal, respectivamente, así como la fluencia por ascenso-deslizamiento por dislocación.

Durante la etapa 1 de deslizamiento fácil, la tasa de endurecimiento por deformación, definida por el cambio en la tensión de corte con respecto a la deformación por deformación ( dτ / dγ ) es baja, representativa de una pequeña cantidad de tensión de corte aplicada necesaria para inducir una gran cantidad de deformación por deformación. El deslizamiento fácil de la dislocación y el flujo correspondiente se atribuyen a la migración de la dislocación solo a lo largo de planos de deslizamiento paralelos (es decir, un sistema de deslizamiento). La impedancia moderada a la migración de la dislocación a lo largo de planos de deslizamiento paralelos se exhibe de acuerdo con las interacciones débiles del campo de tensión entre estas dislocaciones, que aumenta con un espaciamiento interplanar menor. En general, estas dislocaciones migratorias dentro de un solo sistema de deslizamiento actúan como obstáculos débiles para el flujo, y se observa un aumento modesto de la tensión en comparación con la tensión de fluencia. Durante la etapa 2 de endurecimiento lineal del flujo, la tasa de endurecimiento por deformación se vuelve alta ya que se requiere una tensión considerable para superar las interacciones del campo de tensión de las dislocaciones que migran en planos de deslizamiento no paralelos (es decir, múltiples sistemas de deslizamiento), que actúan como fuertes obstáculos para el flujo. Se requiere mucha tensión para impulsar la migración continua de dislocaciones para pequeñas deformaciones. La tensión de flujo de corte es directamente proporcional a la raíz cuadrada de la densidad de dislocaciones (τ flujo ~ ρ ½ ), independientemente de la evolución de las configuraciones de dislocaciones, lo que muestra la dependencia del endurecimiento en el número de dislocaciones presentes. Con respecto a esta evolución de las configuraciones de dislocaciones, en pequeñas deformaciones, la disposición de las dislocaciones es una matriz 3D aleatoria de líneas que se cruzan. Las deformaciones moderadas corresponden a estructuras de dislocaciones celulares de distribución de dislocaciones heterogénea con una gran densidad de dislocaciones en los límites de las celdas y una pequeña densidad de dislocaciones dentro del interior de la celda. En deformaciones incluso mayores, la estructura de dislocación celular se reduce en tamaño hasta que se alcanza un tamaño mínimo. Finalmente, la tasa de endurecimiento por trabajo se vuelve baja nuevamente en el agotamiento/saturación de la etapa de endurecimiento 3 del flujo plástico, ya que pequeñas tensiones de corte producen grandes deformaciones de corte. En particular, en los casos en que múltiples sistemas de deslizamiento están orientados favorablemente con respecto a la tensión aplicada, el τ CRSS para estos sistemas puede ser similar y puede producirse fluencia de acuerdo con la migración de dislocaciones a lo largo de múltiples sistemas de deslizamiento con planos de deslizamiento no paralelos, mostrando una tasa de endurecimiento por trabajo de etapa 1 típicamente característica de la etapa 2. Por último, a continuación se resume la distinción entre la deformación plástica independiente del tiempo en metales de transición cúbicos centrados en el cuerpo y metales cúbicos centrados en las caras.
La plasticidad en los policristales difiere sustancialmente de la de los monocristales debido a la presencia de defectos planos en los límites de grano (GB), que actúan como obstáculos muy fuertes para el flujo plástico al impedir la migración de dislocaciones a lo largo de toda la longitud del plano de deslizamiento activado. Por lo tanto, las dislocaciones no pueden pasar de un grano a otro a través del límite de grano. Las siguientes secciones exploran los requisitos específicos de GB para una deformación plástica extensa de los policristales antes de la fractura, así como la influencia de la fluencia microscópica dentro de los cristalitos individuales en la fluencia macroscópica del policristal. La tensión de corte resuelta crítica para los policristales también se define mediante la ley de Schmid (τ CRSS = σ y / ṁ), donde σ y es la resistencia a la fluencia del policristal y ṁ es el factor de Schmid ponderado. El factor de Schmid ponderado refleja el sistema de deslizamiento menos favorablemente orientado entre los sistemas de deslizamiento más favorablemente orientados de los granos que constituyen el GB.
La restricción GB para policristales puede explicarse considerando un límite de grano en el plano xz entre dos cristales individuales A y B de composición, estructura y sistemas de deslizamiento idénticos, pero desorientados uno con respecto al otro. Para garantizar que no se formen huecos entre los granos que se deforman individualmente, la restricción GB para el bicristal es la siguiente: ε xx A = ε xx B (la deformación axial x en el GB debe ser equivalente para A y B), ε zz A = ε zz B (la deformación axial z en el GB debe ser equivalente para A y B), y ε xz A = ε xz B (la deformación cortante xz a lo largo del plano xz-GB debe ser equivalente para A y B). Además, esta restricción GB requiere que se activen cinco sistemas de deslizamiento independientes por cristalito que constituye el GB. Cabe destacar que, debido a que los sistemas de deslizamiento independientes se definen como planos de deslizamiento en los que las migraciones de dislocaciones no se pueden reproducir mediante ninguna combinación de migraciones de dislocaciones a lo largo de los planos de otros sistemas de deslizamiento, el número de sistemas de deslizamiento geométricos para un sistema cristalino determinado (que, por definición, se puede construir mediante combinaciones de sistemas de deslizamiento) es típicamente mayor que el de sistemas de deslizamiento independientes. Es significativo que exista un máximo de cinco sistemas de deslizamiento independientes para cada uno de los siete sistemas cristalinos; sin embargo, no todos los siete sistemas cristalinos alcanzan este límite superior. De hecho, incluso dentro de un sistema cristalino determinado, la composición y la red de Bravais diversifican el número de sistemas de deslizamiento independientes (véase la tabla siguiente). En los casos en los que los cristalitos de un policristal no obtienen cinco sistemas de deslizamiento independientes, no se puede cumplir la condición de GB y, por lo tanto, la deformación independiente del tiempo de los cristalitos individuales da como resultado grietas y huecos en los GB del policristal y pronto se produce la fractura. Por lo tanto, para una composición y estructura determinadas, un monocristal con menos de cinco sistemas de deslizamiento independientes es más fuerte (exhibe un mayor grado de plasticidad) que su forma policristalina.
Aunque los dos cristalitos A y B analizados en la sección anterior tienen sistemas de deslizamiento idénticos, están desorientados entre sí y, por lo tanto, desorientados con respecto a la fuerza aplicada. Por lo tanto, puede producirse una fluencia microscópica dentro del interior de un cristalito de acuerdo con las reglas que rigen la fluencia independiente del tiempo de un solo cristal. Finalmente, los planos de deslizamiento activados dentro de los interiores de los granos permitirán la migración de dislocaciones al GB, donde muchas dislocaciones se acumulan como dislocaciones geométricamente necesarias. Esta acumulación corresponde a gradientes de deformación a través de granos individuales, ya que la densidad de dislocaciones cerca del GB es mayor que la del interior del grano, lo que impone una tensión en el grano adyacente en contacto. Al considerar el bicristal AB como un todo, el sistema de deslizamiento orientado más favorablemente en A no será el de B y, por lo tanto, τ A CRSS ≠ τ B CRSS . Es primordial el hecho de que la fluencia macroscópica del bicristal se prolonga hasta que se alcanza el valor más alto de τ CRSS entre los granos A y B, de acuerdo con la restricción del GB. Por lo tanto, para una composición y estructura dadas, un policristal con cinco sistemas de deslizamiento independientes es más fuerte (mayor grado de plasticidad) que su forma monocristalina. En consecuencia, la tasa de endurecimiento por deformación será mayor para el policristal que para el monocristal, ya que se requiere más tensión en el policristal para producir deformaciones. Es importante destacar que, al igual que con la tensión de flujo del monocristal, τ flujo ~ρ ½ , pero también es inversamente proporcional a la raíz cuadrada del diámetro de grano promedio (τ flujo ~d -½ ). Por lo tanto, la tensión de flujo de un policristal, y por lo tanto la resistencia del policristal, aumenta con un tamaño de grano pequeño. La razón de esto es que los granos más pequeños tienen un número relativamente menor de planos de deslizamiento para activarse, lo que corresponde a un menor número de dislocaciones que migran a los GB y, por lo tanto, menos tensión inducida en los granos adyacentes debido a la acumulación de dislocaciones. Además, para un volumen dado de policristal, los granos más pequeños presentan límites de grano de obstáculos más fuertes. Estos dos factores permiten comprender por qué el inicio del flujo macroscópico en policristales de grano fino ocurre cuando se aplican tensiones mayores que en policristales de grano grueso.

Existen varias descripciones matemáticas de la plasticidad. [12] Una de ellas es la teoría de la deformación (véase, por ejemplo , la ley de Hooke ), en la que el tensor de tensión de Cauchy (de orden d-1 en dimensiones d) es una función del tensor de deformación. Aunque esta descripción es precisa cuando una pequeña parte de la materia está sujeta a una carga creciente (como una carga de deformación), esta teoría no puede explicar la irreversibilidad.
Los materiales dúctiles pueden soportar grandes deformaciones plásticas sin fracturarse . Sin embargo, incluso los metales dúctiles se fracturarán cuando la tensión sea lo suficientemente grande, como resultado del endurecimiento del material, que lo vuelve frágil . El tratamiento térmico, como el recocido, puede restaurar la ductilidad de una pieza trabajada, de modo que se pueda continuar moldeando.
En 1934, Egon Orowan , Michael Polanyi y Geoffrey Ingram Taylor , casi simultáneamente, se dieron cuenta de que la deformación plástica de los materiales dúctiles podía explicarse en términos de la teoría de las dislocaciones . La teoría matemática de la plasticidad, la teoría de la plasticidad de flujo , utiliza un conjunto de ecuaciones no lineales y no integrables para describir el conjunto de cambios en la deformación y la tensión con respecto a un estado anterior y un pequeño aumento de la deformación.

Si la tensión supera un valor crítico, como se mencionó anteriormente, el material sufrirá una deformación plástica o irreversible. Esta tensión crítica puede ser de tracción o compresión. Los criterios de Tresca y de von Mises se utilizan comúnmente para determinar si un material ha cedido. Sin embargo, estos criterios han demostrado ser inadecuados para una amplia gama de materiales y también se utilizan ampliamente otros criterios de fluencia.
El criterio de Tresca se basa en la noción de que cuando un material falla, lo hace por esfuerzo cortante, lo cual es una suposición relativamente buena cuando se consideran metales. Dado el estado de tensión principal, podemos usar el círculo de Mohr para calcular las tensiones cortantes máximas que experimentará nuestro material y concluir que el material fallará si
donde σ 1 es la tensión normal máxima, σ 3 es la tensión normal mínima y σ 0 es la tensión bajo la cual el material falla en carga uniaxial. Se puede construir una superficie de fluencia , que proporciona una representación visual de este concepto. Dentro de la superficie de fluencia, la deformación es elástica. En la superficie, la deformación es plástica. Es imposible que un material tenga estados de tensión fuera de su superficie de fluencia.
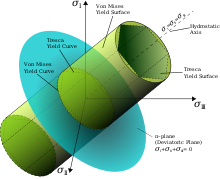
El criterio de Huber-von Mises [13] se basa en el criterio de Tresca, pero tiene en cuenta el supuesto de que las tensiones hidrostáticas no contribuyen a la falla del material. MT Huber fue el primero en proponer el criterio de energía de corte. [14] [15] Von Mises resuelve una tensión efectiva bajo carga uniaxial, restando las tensiones hidrostáticas, y afirma que todas las tensiones efectivas mayores que la que causa la falla del material en carga uniaxial darán como resultado una deformación plástica.
Nuevamente, se puede construir una representación visual de la superficie de fluencia utilizando la ecuación anterior, que toma la forma de una elipse. Dentro de la superficie, los materiales sufren una deformación elástica. Al llegar a la superficie, el material sufre deformaciones plásticas.
{{cite book}}: CS1 maint: location missing publisher (link)