Principio de inclusión-exclusión

Técnica de conteo en combinatoria.

Diagrama de Venn que muestra la unión de los conjuntos A y B como todo lo que no está en blanco.

En combinatoria , una rama de las matemáticas , el principio de inclusión-exclusión es una técnica de conteo que generaliza el método familiar de obtener el número de elementos en la unión de dos conjuntos finitos ; expresado simbólicamente como

${\displaystyle |A\cup B|=|A|+|B|-|A\cap B|}$

donde A y B son dos conjuntos finitos y | S | indica la cardinalidad de un conjunto S (que puede considerarse como el número de elementos del conjunto, si el conjunto es finito ). La fórmula expresa el hecho de que la suma de los tamaños de los dos conjuntos puede ser demasiado grande ya que algunos elementos pueden contarse dos veces. Los elementos contados dos veces son aquellos en la intersección de los dos conjuntos y el recuento se corrige restando el tamaño de la intersección.

El principio de inclusión-exclusión, al ser una generalización del caso de dos conjuntos, quizás se vea más claramente en el caso de tres conjuntos, que para los conjuntos A , B y C viene dado por

${\displaystyle |A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|}$

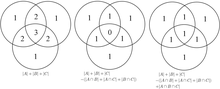
Esta fórmula se puede verificar contando cuántas veces cada región en la figura del diagrama de Venn se incluye en el lado derecho de la fórmula. En este caso, al eliminar las contribuciones de los elementos contados en exceso, el número de elementos en la intersección mutua de los tres conjuntos se ha restado con demasiada frecuencia, por lo que se debe volver a sumar para obtener el total correcto.

Inclusión-exclusión ilustrada por un diagrama de Venn para tres conjuntos

Al generalizar los resultados de estos ejemplos se obtiene el principio de inclusión-exclusión. Para encontrar la cardinalidad de la unión de n conjuntos:

1. Incluye las cardinalidades de los conjuntos.
2. Excluir las cardinalidades de las intersecciones por pares.
3. Incluya las cardinalidades de las intersecciones triples.
4. Excluye las cardinalidades de las intersecciones cuádruples.
5. Incluya las cardinalidades de las intersecciones quíntuples.
6. Continúe hasta que se incluya la cardinalidad de la intersección de n tuplas (si n es impar) o se excluya ( n par).

El nombre proviene de la idea de que el principio se basa en una inclusión excesivamente generosa , seguida de una exclusión compensatoria . Este concepto se atribuye a Abraham de Moivre (1718), ^[1] aunque aparece por primera vez en un artículo de Daniel da Silva (1854) ^[2] y posteriormente en un artículo de JJ Sylvester (1883). ^[3] A veces se hace referencia al principio como la fórmula de Da Silva o Sylvester, debido a estas publicaciones. El principio puede verse como un ejemplo del método de tamiz ampliamente utilizado en teoría de números y, a veces, se lo denomina fórmula de tamiz . ^[4]

Como las probabilidades finitas se calculan como recuentos relativos a la cardinalidad del espacio de probabilidad , las fórmulas para el principio de inclusión-exclusión siguen siendo válidas cuando las cardinalidades de los conjuntos se reemplazan por probabilidades finitas. De manera más general, ambas versiones del principio pueden ubicarse bajo el paraguas común de la teoría de la medida .

En un entorno muy abstracto, el principio de inclusión-exclusión puede expresarse como el cálculo de la inversa de una determinada matriz. ^[5] Esta inversa tiene una estructura especial, lo que hace que el principio sea una técnica extremadamente valiosa en combinatoria y áreas relacionadas de las matemáticas. Como dijo Gian-Carlo Rota : ^[6]

"Uno de los principios de enumeración más útiles en probabilidad discreta y teoría combinatoria es el célebre principio de inclusión-exclusión. Cuando se aplica hábilmente, este principio ha dado la solución a muchos problemas combinatorios".

Fórmula

En su fórmula general, el principio de inclusión-exclusión establece que para conjuntos finitos A ₁ ,…, An _, se tiene la identidad

Cada término de la fórmula de inclusión-exclusión corrige gradualmente el conteo hasta que finalmente cada porción del diagrama de Venn se cuenta exactamente una vez.

Esto se puede escribir de forma compacta como

${\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leqslant i_{1}<\cdots <i_{k}\leqslant n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)}$

o

${\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{\emptyset \neq J\subseteq \{1,\ldots ,n\}}(-1)^{|J|+1}\left|\bigcap _{j\in J}A_{j}\right|.}$

En palabras, para contar el número de elementos en una unión finita de conjuntos finitos, primero sume las cardinalidades de los conjuntos individuales, luego reste el número de elementos que aparecen en al menos dos conjuntos, luego vuelva a sumar el número de elementos que aparecen en al menos tres conjuntos, luego resta el número de elementos que aparecen en al menos cuatro conjuntos, y así sucesivamente. Este proceso siempre termina ya que no puede haber elementos que aparezcan en más del número de conjuntos de la unión. (Por ejemplo, si no puede haber elementos que aparezcan en más de conjuntos; de manera equivalente, no puede haber elementos que aparezcan en al menos conjuntos). ${\displaystyle n=4,}$ ${\displaystyle 4}$ ${\displaystyle 5}$

En las aplicaciones es común ver el principio expresado en su forma complementaria. Es decir, considerando que _S es un conjunto universal finito que contiene todos los Ai y denotando el complemento de _Ai en S , según las leyes de De Morgan tenemos ${\displaystyle {\bar {A_{i}}}}$

${\displaystyle \left|\bigcap _{i=1}^{n}{\bar {A_{i}}}\right|=\left|S-\bigcup _{i=1}^{n}A_{i}\right|=|S|-\sum _{i=1}^{n}|A_{i}|+\sum _{1\leqslant i<j\leqslant n}|A_{i}\cap A_{j}|-\cdots +(-1)^{n}|A_{1}\cap \cdots \cap A_{n}|.}$

Como otra variante del enunciado, sea P ₁ , ..., P _n una lista de propiedades que los elementos de un conjunto S pueden tener o no, entonces el principio de inclusión-exclusión proporciona una manera de calcular el número de elementos de S que no tienen ninguna de las propiedades. Simplemente dejemos que _A i _sea el subconjunto de elementos de S que tienen la propiedad Pi y usan el principio en su forma complementaria. Esta variante se debe a JJ Sylvester . ^[1]

Observe que si toma en cuenta solo las primeras m<n sumas de la derecha (en la forma general del principio), obtendrá una sobreestimación si m es impar y una subestimación si m es par.

Ejemplos

Trastornos de conteo

Un ejemplo más complejo es el siguiente.

Supongamos que hay una baraja de n cartas numeradas del 1 al  n . Supongamos que una carta con el número m está en la posición correcta si es la enésima carta de la baraja. ¿De cuántas maneras, W , se pueden barajar las cartas con al menos una carta en la posición correcta?

Comience por definir el conjunto _Am , que son todos los ordenamientos de las tarjetas con la m enésima tarjeta correcta. Entonces el número de órdenes, W , con al menos una tarjeta en la posición correcta, m , es

${\displaystyle W=\left|\bigcup _{m=1}^{n}A_{m}\right|.}$

Aplicar el principio de inclusión-exclusión,

${\displaystyle W=\sum _{m_{1}=1}^{n}|A_{m_{1}}|-\sum _{1\leqslant m_{1}<m_{2}\leqslant n}|A_{m_{1}}\cap A_{m_{2}}|+\cdots +(-1)^{p-1}\sum _{1\leqslant m_{1}<\cdots <m_{p}\leqslant n}|A_{m_{1}}\cap \cdots \cap A_{m_{p}}|+\cdots }$

Cada valor representa el conjunto de combinaciones que tienen al menos valores p m ₁ ,…,  m _p en la posición correcta. Tenga en cuenta que el número de mezclas con al menos p valores correctos solo depende de p , no de los valores particulares de . Por ejemplo, el número de barajas que tienen las cartas 1.ª, 3.ª y 17.ª en la posición correcta es el mismo que el número de barajaciones que tienen las cartas 2.ª, 5.ª y 13.ª en las posiciones correctas. Sólo importa que de las n cartas se escogieron 3 por estar en la posición correcta. Por lo tanto, hay términos iguales en la p -ésima suma (ver combinación ). ${\displaystyle A_{m_{1}}\cap \cdots \cap A_{m_{p}}}$ ${\displaystyle m}$ ${\textstyle {n \choose p}}$

${\displaystyle W={n \choose 1}|A_{1}|-{n \choose 2}|A_{1}\cap A_{2}|+\cdots +(-1)^{p-1}{n \choose p}|A_{1}\cap \cdots \cap A_{p}|+\cdots }$

${\displaystyle |A_{1}\cap \cdots \cap A_{p}|}$es el número de ordenamientos que tienen p elementos en la posición correcta, que es igual al número de formas de ordenar los n  −  p elementos restantes, o ( n  −  p )!. Así finalmente obtenemos:

${\displaystyle {\begin{aligned}W&={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+\cdots +(-1)^{p-1}{n \choose p}(n-p)!+\cdots \\&=\sum _{p=1}^{n}(-1)^{p-1}{n \choose p}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!(n-p)!}}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!}}\end{aligned}}}$

Una permutación en la que ninguna carta está en la posición correcta se llama trastorno . Tomando n ! para ser el número total de permutaciones, la probabilidad Q de que una mezcla aleatoria produzca un trastorno está dada por

${\displaystyle Q=1-{\frac {W}{n!}}=\sum _{p=0}^{n}{\frac {(-1)^{p}}{p!}},}$

un truncamiento a n  + 1 términos de la expansión de Taylor de e ⁻¹ . Por lo tanto, la probabilidad de adivinar el orden de una baraja de cartas barajada y equivocarse con cada carta es aproximadamente e ⁻¹ o 37%.

Un caso especial

La situación que aparece en el ejemplo anterior del trastorno ocurre con suficiente frecuencia como para merecer una atención especial. ^[7] Es decir, cuando el tamaño de los conjuntos de intersecciones que aparecen en las fórmulas para el principio de inclusión-exclusión depende sólo del número de conjuntos en las intersecciones y no de qué conjuntos aparecen. Más formalmente, si la intersección

${\displaystyle A_{J}:=\bigcap _{j\in J}A_{j}}$

tiene la misma cardinalidad, digamos α _k = | A _J |, para cada subconjunto J de k elementos de {1,…,  n }, entonces

${\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.}$

O, en la forma complementaria, donde el conjunto universal S tiene cardinalidad α ₀ ,

${\displaystyle \left|S\smallsetminus \bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\alpha _{k}.}$

Generalización de fórmulas

Dada una familia (se permiten repeticiones) de subconjuntos A ₁ , A ₂ , ..., An _de un conjunto universal S , el principio de inclusión-exclusión calcula el número de elementos de S en ninguno de estos subconjuntos. Una generalización de este concepto calcularía el número de elementos de S que aparecen exactamente en algún m fijo de estos conjuntos.

Sea N = [ n ] = {1,2,…, n }. Si definimos , entonces el principio de inclusión-exclusión se puede escribir como, usando la notación de la sección anterior; el número de elementos de S contenidos en ninguno de los Ai _es : ${\displaystyle A_{\emptyset }=S}$

${\displaystyle \sum _{J\subseteq [n]}(-1)^{|J|}|A_{J}|.}$

Si I es un subconjunto fijo del conjunto de índices N , entonces el número de elementos que pertenecen a _Ai para todo i en I y para ningún otro valor es: ^[8]

${\displaystyle \sum _{I\subseteq J}(-1)^{|J|-|I|}|A_{J}|.}$

Definir los conjuntos

${\displaystyle B_{k}=A_{I\cup \{k\}}{\text{ for }}k\in N\smallsetminus I.}$

Buscamos el número de elementos en ninguno de los B _k que, por el principio de inclusión-exclusión (con ), es ${\displaystyle B_{\emptyset }=A_{I}}$

${\displaystyle \sum _{K\subseteq N\smallsetminus I}(-1)^{|K|}|B_{K}|.}$

La correspondencia K ↔ J = I ∪ K entre subconjuntos de N  \  I y subconjuntos de N que contienen I es una biyección y si J y K corresponden bajo este mapa entonces B _K = A _J , lo que demuestra que el resultado es válido.

En probabilidad

En probabilidad , para eventos A ₁ , ..., An en un espacio de probabilidad , el principio _de inclusión-exclusión se vuelve para n  = 2 ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$

${\displaystyle \mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),}$

para norte  = 3

${\displaystyle \mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})}$

y en general

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{i=1}^{n}\mathbb {P} (A_{i})-\sum _{i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i<j<k}\mathbb {P} (A_{i}\cap A_{j}\cap A_{k})+\cdots +(-1)^{n-1}\sum _{i<...<n}\mathbb {P} \left(\bigcap _{i=1}^{n}A_{i}\right),}$

que se puede escribir en forma cerrada como

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{I\subseteq \{1,\ldots ,n\} \atop |I|=k}\mathbb {P} (A_{I})\right),}$

donde la última suma abarca todos los subconjuntos I de los índices 1,…, n que contienen exactamente k elementos, y

${\displaystyle A_{I}:=\bigcap _{i\in I}A_{i}}$

denota la intersección de todos aquellos A _i con índice en I .

Según las desigualdades de Bonferroni , la suma de los primeros términos de la fórmula es alternativamente un límite superior y un límite inferior para el LHS . Esto se puede utilizar en los casos en que la fórmula completa sea demasiado engorrosa.

Para un espacio de medida general ( S ,Σ, μ ) y subconjuntos medibles A ₁ , …, An _de medida finita, las identidades anteriores también se mantienen cuando la medida de probabilidad se reemplaza por la medida μ . ${\displaystyle \mathbb {P} }$

Caso especial

Si, en la versión probabilística del principio de inclusión-exclusión, la probabilidad de la intersección A _I sólo depende de la cardinalidad de I , es decir que para cada k en {1,…,  n } existe un a _k tal que

${\displaystyle a_{k}=\mathbb {P} (A_{I}){\text{ for every }}I\subset \{1,\ldots ,n\}{\text{ with }}|I|=k,}$

entonces la fórmula anterior se simplifica a

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}}$

debido a la interpretación combinatoria del coeficiente binomial . Por ejemplo, si los eventos son independientes y están distribuidos idénticamente , entonces para todo i , y tenemos , en cuyo caso la expresión anterior se simplifica a ${\textstyle {\binom {n}{k}}}$ ${\displaystyle A_{i}}$ ${\displaystyle \mathbb {P} (A_{i})=p}$ ${\displaystyle a_{k}=p^{k}}$

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=1-(1-p)^{n}.}$

(Este resultado también se puede derivar de manera más simple considerando la intersección de los complementos de los eventos ). ${\displaystyle A_{i}}$

Una simplificación análoga es posible en el caso de un espacio de medida general ( S , Σ, μ ) y subconjuntos medibles A ₁ , …, An _de medida finita.

Otras fórmulas

El principio a veces se expresa en la forma ^[9] que dice que si

${\displaystyle g(A)=\sum _{S\subseteq A}f(S)}$

entonces

La versión combinatoria y probabilística del principio de inclusión-exclusión son ejemplos de ( 2 ).

Prueba

Toma , y ${\displaystyle {\underline {m}}=\{1,2,\ldots ,m\}}$ ${\displaystyle f({\underline {m}})=0}$

${\displaystyle f(S)=\left|\bigcap _{i\in {\underline {m}}\smallsetminus S}A_{i}\smallsetminus \bigcup _{i\in S}A_{i}\right|{\text{ and }}f(S)=\mathbb {P} \left(\bigcap _{i\in {\underline {m}}\smallsetminus S}A_{i}\smallsetminus \bigcup _{i\in S}A_{i}\right)}$

respectivamente para todos los conjuntos con . Entonces obtenemos ${\displaystyle S}$ ${\displaystyle S\subsetneq {\underline {m}}}$

${\displaystyle g(A)=\left|\bigcap _{i\in {\underline {m}}\smallsetminus A}A_{i}\right|,\quad g({\underline {m}})=\left|\bigcup _{i\in {\underline {m}}}A_{i}\right|{\text{ and }}g(A)=\mathbb {P} \left(\bigcap _{i\in {\underline {m}}\smallsetminus A}A_{i}\right),~~g({\underline {m}})=\mathbb {P} \left(\bigcup _{i\in {\underline {m}}}A_{i}\right)}$

respectivamente para todos los conjuntos con . Esto se debe a que los elementos de también pueden estar contenidos en other ( with ), y la fórmula se ejecuta exactamente a través de todas las extensiones posibles de los conjuntos with other , contando solo para el conjunto que coincide con el comportamiento de membresía de , if se ejecuta en todos los subconjuntos de (como en la definición de ). ${\displaystyle A}$ ${\displaystyle A\subsetneq {\underline {m}}}$ ${\displaystyle a}$ ${\displaystyle \cap _{i\in {\underline {m}}\smallsetminus A}A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle i\in A}$ ${\displaystyle \cap \smallsetminus \cup }$ ${\displaystyle \{A_{i}\mid i\in {\underline {m}}\smallsetminus A\}}$ ${\displaystyle A_{i}}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle S}$ ${\displaystyle A}$ ${\displaystyle g(A)}$

Ya que obtenemos de ( 2 ) con eso ${\displaystyle f({\underline {m}})=0}$ ${\displaystyle A={\underline {m}}}$

${\displaystyle \sum _{{\underline {m}}\supseteq T\supsetneq \varnothing }(-1)^{|T|-1}g({\underline {m}}\smallsetminus T)=\sum _{\varnothing \subseteq S\subsetneq {\underline {m}}}(-1)^{m-|S|-1}g(S)=g({\underline {m}})}$

y al intercambiar lados, se siguen la versión combinatoria y probabilística del principio de inclusión-exclusión.

Si uno ve un número como un conjunto de sus factores primos, entonces ( 2 ) es una generalización de la fórmula de inversión de Möbius para números naturales libres de cuadrados . Por lo tanto, ( 2 ) se considera la fórmula de inversión de Möbius para el álgebra de incidencia del conjunto parcialmente ordenado de todos los subconjuntos de A. ${\displaystyle n}$

Para una generalización de la versión completa de la fórmula de inversión de Möbius, ( 2 ) debe generalizarse a conjuntos múltiples . Para conjuntos múltiples en lugar de conjuntos, ( 2 ) se convierte

¿Dónde está el conjunto múltiple para qué , y ${\displaystyle A-S}$ ${\displaystyle (A-S)\uplus S=A}$

• μ ( S ) = 1 si S es un conjunto (es decir, un conjunto múltiple sin elementos dobles) de cardinalidad par .
• μ ( S ) = −1 si S es un conjunto (es decir, un conjunto múltiple sin elementos dobles) de cardinalidad impar.
• μ ( S ) = 0 si S es un conjunto múltiple adecuado (es decir, S tiene elementos dobles).

Observe que es solo el de ( 2 ) en caso de que sea un conjunto. ${\displaystyle \mu (A-S)}$ ${\displaystyle (-1)^{|A|-|S|}}$ ${\displaystyle A-S}$

Prueba de ( 3 )

Sustituto

$${\displaystyle g(S)=\sum _{T\subseteq S}f(T)}$$

en el lado derecho de ( 3 ). Observe que aparece una vez a ambos lados de ( 3 ). Entonces debemos demostrar que para todos los términos con , los términos se cancelan en el lado derecho de ( 3 ). Para ello, tome un fijo tal que y tome un fijo arbitrario tal que . ${\displaystyle f(A)}$ ${\displaystyle T}$ ${\displaystyle T\subsetneq A}$ ${\displaystyle f(T)}$ ${\displaystyle T}$ ${\displaystyle T\subsetneq A}$ ${\displaystyle a\in A}$ ${\displaystyle a\notin T}$

Observe que debe haber un conjunto para cada aparición positiva o negativa de en el lado derecho de ( 3 ) que se obtiene mediante el multiconjunto tal que . Ahora cada aparición de en el lado derecho de ( 3 ) que se obtiene mediante el conjunto que contiene se cancela con la que se obtiene mediante el correspondiente conjunto que no contiene . Esto da el resultado deseado. ${\displaystyle A-S}$ ${\displaystyle f(T)}$ ${\displaystyle S}$ ${\displaystyle T\subseteq S\subseteq A}$ ${\displaystyle f(T)}$ ${\displaystyle S}$ ${\displaystyle A-S}$ ${\displaystyle a}$ ${\displaystyle S}$ ${\displaystyle A-S}$ ${\displaystyle a}$

Aplicaciones

El principio de inclusión-exclusión se utiliza ampliamente y aquí sólo podemos mencionar algunas de sus aplicaciones.

Trastornos de conteo

Una aplicación bien conocida del principio de inclusión-exclusión es al problema combinatorio de contar todos los trastornos de un conjunto finito. Un trastorno de un conjunto A es una biyección de A hacia sí mismo que no tiene puntos fijos. A través del principio de inclusión-exclusión se puede demostrar que si la cardinalidad de A es n , entonces el número de trastornos es [ n ! /  e ] donde [ x ] denota el número entero más cercano a x ; una prueba detallada está disponible aquí y también consulte la sección de ejemplos anterior.

La primera aparición del problema de contar el número de trastornos se encuentra en uno de los primeros libros sobre juegos de azar: Essai d'analyse sur les jeux de Hazard de PR de Montmort (1678 - 1719) y se conocía como "el problema de Montmort" o por el nombre que le dio, " problème des rencontres ". ^[10] El problema también se conoce como problema de hatcheck.

El número de trastornos también se conoce como subfactorial de n , escrito ! n . De ello se deduce que si a todas las biyecciones se les asigna la misma probabilidad, entonces la probabilidad de que una biyección aleatoria sea un trastorno se aproxima rápidamente a 1/ e a medida que n crece.

Contando intersecciones

El principio de inclusión-exclusión, combinado con la ley de De Morgan , también se puede utilizar para contar la cardinalidad de la intersección de conjuntos. Representemos el complemento de A _k con respecto a algún conjunto universal A tal que para cada k . Entonces nosotros tenemos ${\displaystyle {\overline {A_{k}}}}$ ${\displaystyle A_{k}\subseteq A}$

${\displaystyle \bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A_{i}}}}}}$

convirtiendo así el problema de encontrar una intersección en el problema de encontrar una unión.

Coloración de gráficos

El principio de inclusión y exclusión forma la base de los algoritmos para una serie de problemas de partición de gráficos NP-hard, como la coloración de gráficos. ^[11]

Una aplicación bien conocida del principio es la construcción del polinomio cromático de un gráfico. ^[12]

Emparejamientos perfectos de gráficos bipartitos

El número de coincidencias perfectas de un gráfico bipartito se puede calcular utilizando el principio. ^[13]

Número de funciones on

Dados los conjuntos finitos A y B , ¿cuántas funciones sobreyectivas (sobre funciones) hay de A a B ? Sin pérdida de generalidad, podemos tomar A = {1,..., k } y B = {1,..., n }, ya que sólo importan las cardinalidades de los conjuntos. Al usar S como el conjunto de todas las funciones de A a B y definir, para cada i en B , la propiedad P _i como "la función omite el elemento i en B " ( i no está en la imagen de la función), el principio de inclusión-exclusión da el número de funciones onto entre A y B como: ^[14]

${\displaystyle \sum _{j=0}^{n}{\binom {n}{j}}(-1)^{j}(n-j)^{k}.}$

Permutaciones con posiciones prohibidas

Una permutación del conjunto S = {1, ..., n } donde cada elemento de S está restringido a no estar en ciertas posiciones (aquí la permutación se considera como un ordenamiento de los elementos de S ) se llama permutación con prohibido posiciones . Por ejemplo, con S = {1,2,3,4}, las permutaciones con la restricción de que el elemento 1 no puede estar en las posiciones 1 o 3, y el elemento 2 no puede estar en la posición 4 son: 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 y 4321. Dejando que A _i sea el conjunto de posiciones en las que no se le permite estar al elemento i , y que la propiedad P _i sea la propiedad que una permutación coloca al elemento i en una posición en Ai _, el principio de inclusión-exclusión se puede utilizar para contar el número de permutaciones que satisfacen todas las restricciones. ^[15]

En el ejemplo dado, hay 12 = 2(3!) permutaciones con propiedad P ₁ , 6 = 3! las permutaciones con propiedad P ₂ y ninguna permutación tiene propiedades P ₃ o P ₄ ya que no hay restricciones para estos dos elementos. El número de permutaciones que satisfacen las restricciones es entonces:

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

Los últimos 4 en este cálculo son el número de permutaciones que tienen ambas propiedades P ₁ y P ₂ . No hay otras contribuciones distintas de cero a la fórmula.

Números de Stirling de segunda especie.

Los números de Stirling de segunda clase , S ( n , k ), cuentan el número de particiones de un conjunto de n elementos en k subconjuntos no vacíos ( cajas indistinguibles ). Se puede obtener una fórmula explícita para ellos aplicando el principio de inclusión-exclusión a un problema muy estrechamente relacionado, a saber, contar el número de particiones de un n -conjunto en k cajas no vacías pero distinguibles ( subconjuntos ordenados no vacíos). . Usando el conjunto universal que consta de todas las particiones del n -conjunto en k (posiblemente vacías) cajas distinguibles, A ₁ , A ₂ ,…, A _k , y las propiedades P _i que significan que la partición tiene la caja Ai _vacía , el principio de inclusión-exclusión da una respuesta para el resultado relacionado. Dividiendo por k ! para eliminar el orden artificial se obtiene el número de Stirling del segundo tipo: ^[16]

${\displaystyle S(n,k)={\frac {1}{k!}}\sum _{t=0}^{k}(-1)^{t}{\binom {k}{t}}(k-t)^{n}.}$

Polinomios de torre

Un polinomio de torres es la función generadora del número de formas de colocar torres no atacantes en un tablero B que parece un subconjunto de las casillas de un tablero de ajedrez ; es decir, no pueden haber dos torres en la misma fila o columna. El tablero B es cualquier subconjunto de los cuadrados de un tablero rectangular con n filas ym columnas; Pensamos en ello como las casillas en las que se permite colocar una torre. El coeficiente , r _k ( B ) de x ^k en el polinomio de la torre R _B ( x ) es el número de formas en que k torres , ninguna de las cuales ataca a otra, pueden disponerse en los cuadrados de B. Para cualquier tablero B , existe un tablero complementario formado por las casillas del tablero rectangular que no están en B. Este tablero complementario también tiene un polinomio de torre con coeficientes ${\displaystyle B'}$ ${\displaystyle R_{B'}(x)}$ ${\displaystyle r_{k}(B').}$

A veces es conveniente poder calcular el coeficiente más alto de un polinomio de torre en términos de los coeficientes del polinomio de torre del tablero complementario. Sin pérdida de generalidad podemos suponer que n ≤ m , por lo que este coeficiente es r _n ( B ). El número de formas de colocar n torres no atacantes en el "tablero de ajedrez" completo de n × m (sin tener en cuenta si las torres están colocadas en las casillas del tablero B ) viene dada por el factorial descendente :

${\displaystyle (m)_{n}=m(m-1)(m-2)\cdots (m-n+1).}$

Suponiendo que P _i sea la propiedad de que una asignación de n torres no atacantes en el tablero completo tiene una torre en la columna i que no está en un cuadrado del tablero B , entonces, según el principio de inclusión-exclusión, tenemos: ^[17]

${\displaystyle r_{n}(B)=\sum _{t=0}^{n}(-1)^{t}(m-t)_{n-t}r_{t}(B').}$

Función phi de Euler

La función totient o phi de Euler, φ ( n ) es una función aritmética que cuenta el número de enteros positivos menores o iguales que n que son primos relativos con n . Es decir, si n es un entero positivo , entonces φ( n ) es el número de enteros k en el rango 1 ≤ k ≤ n que no tienen ningún factor común con n distinto de 1. El principio de inclusión-exclusión se utiliza para obtener una fórmula para φ( n ). Sea S el conjunto {1,…, n } y defina la propiedad P _i como que un número en S es divisible por el número primo p _i , para 1 ≤ i ≤ r , donde la factorización prima de

${\displaystyle n=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{r}^{a_{r}}.}$

Entonces, ^[18]

${\displaystyle \varphi (n)=n-\sum _{i=1}^{r}{\frac {n}{p_{i}}}+\sum _{1\leqslant i<j\leqslant r}{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i}}}\right).}$

Método de la hipérbola de Dirichlet

Un ejemplo del método de la hipérbola de Dirichlet con y ${\displaystyle n=10,}$ ${\displaystyle a\approx 2.7,}$ ${\displaystyle b\approx 3.7.}$

El método de la hipérbola de Dirichlet reexpresa una suma de una función multiplicativa seleccionando una convolución de Dirichlet adecuada , reconociendo que la suma ${\displaystyle f(n)}$ ${\displaystyle f=g\ast h}$

${\displaystyle F(n)=\sum _{k=1}^{n}f(k)=\sum _{k=1}^{n}\sum _{xy=k}^{}g(x)h(y)}$

se puede reformular como una suma sobre los puntos de la red en una región delimitada por , y , dividiendo esta región en dos subregiones superpuestas y finalmente usando el principio de inclusión-exclusión para concluir que ${\displaystyle x\geq 1}$ ${\displaystyle y\geq 1}$ ${\displaystyle xy\leq n}$

${\displaystyle F(n)=\sum _{k=1}^{n}f(k)=\sum _{k=1}^{n}\sum _{xy=k}^{}g(x)h(y)=\sum _{x=1}^{a}\sum _{y=1}^{n/x}g(x)h(y)+\sum _{y=1}^{b}\sum _{x=1}^{n/y}g(x)h(y)-\sum _{x=1}^{a}\sum _{y=1}^{b}g(x)h(y).}$

Principio de inclusión-exclusión diluida

En muchos casos en los que el principio podría dar una fórmula exacta (en particular, contar números primos usando el tamiz de Eratóstenes ), la fórmula que surge no ofrece un contenido útil porque el número de términos que contiene es excesivo. Si cada término individualmente puede estimarse con precisión, la acumulación de errores puede implicar que la fórmula de inclusión-exclusión no sea directamente aplicable. En teoría de números , esta dificultad fue abordada por Viggo Brun . Después de un comienzo lento, sus ideas fueron adoptadas por otros y se desarrolló una gran variedad de métodos de tamizado . Estos, por ejemplo, pueden intentar encontrar límites superiores para los conjuntos "tamizados", en lugar de una fórmula exacta.

Sean A ₁ , ..., An _conjuntos arbitrarios y p ₁ , ..., p _n números reales en el intervalo unitario cerrado [0, 1] . Entonces, para cada número par k en {0,…, n }, las funciones indicadoras satisfacen la desigualdad: ^[19]

${\displaystyle 1_{A_{1}\cup \cdots \cup A_{n}}\geq \sum _{j=1}^{k}(-1)^{j-1}\sum _{1\leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.}$

Prueba de declaración principal

Elija un elemento contenido en la unión de todos los conjuntos y sean los conjuntos individuales que lo contienen. (Tenga en cuenta que t > 0.) Dado que el elemento se cuenta exactamente una vez en el lado izquierdo de la ecuación ( 1 ), debemos demostrar que se cuenta exactamente una vez en el lado derecho. En el lado derecho, las únicas contribuciones distintas de cero ocurren cuando todos los subconjuntos de un término particular contienen el elemento elegido, es decir, todos los subconjuntos se seleccionan de . La contribución es una para cada uno de estos conjuntos (más o menos según el término) y, por lo tanto, es solo el número (con signo) de estos subconjuntos utilizados en el término. Entonces tenemos: ${\displaystyle A_{1},A_{2},\dots ,A_{t}}$ ${\displaystyle A_{1},A_{2},\dots ,A_{t}}$

${\displaystyle {\begin{aligned}|\{A_{i}\mid 1\leqslant i\leqslant t\}|&-|\{A_{i}\cap A_{j}\mid 1\leqslant i<j\leqslant t\}|+\cdots +(-1)^{t+1}|\{A_{1}\cap A_{2}\cap \cdots \cap A_{t}\}|={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}}.\end{aligned}}}$

Por el teorema del binomio ,

${\displaystyle 0=(1-1)^{t}={\binom {t}{0}}-{\binom {t}{1}}+{\binom {t}{2}}-\cdots +(-1)^{t}{\binom {t}{t}}.}$

Usando el hecho de que y reordenando los términos, tenemos ${\displaystyle {\binom {t}{0}}=1}$

${\displaystyle 1={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}},}$

y así, el elemento elegido se cuenta solo una vez en el lado derecho de la ecuación ( 1 ).

prueba algebraica

Se puede obtener una prueba algebraica utilizando funciones indicadoras (también conocidas como funciones características). La función indicadora de un subconjunto S de un conjunto X es la función

${\displaystyle {\begin{aligned}&\mathbf {1} _{S}:X\to \{0,1\}\\&\mathbf {1} _{S}(x)={\begin{cases}1&x\in S\\0&x\notin S\end{cases}}\end{aligned}}}$

Si y son dos subconjuntos de , entonces ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle X}$

${\displaystyle \mathbf {1} _{A}\cdot \mathbf {1} _{B}=\mathbf {1} _{A\cap B}.}$

Sea A la unión de los conjuntos A ₁ ,…, An _. Para probar el principio de inclusión-exclusión en general, primero verificamos la identidad ${\textstyle \bigcup _{i=1}^{n}A_{i}}$

para funciones indicadoras, donde:

${\displaystyle A_{I}=\bigcap _{i\in I}A_{i}.}$

La siguiente función

${\displaystyle \left(\mathbf {1} _{A}-\mathbf {1} _{A_{1}}\right)\left(\mathbf {1} _{A}-\mathbf {1} _{A_{2}}\right)\cdots \left(\mathbf {1} _{A}-\mathbf {1} _{A_{n}}\right),}$

es idénticamente cero porque: si x no está en A , entonces todos los factores son 0 − 0 = 0; y de lo contrario, si x pertenece a algún Am , entonces el m _- ^ésimo factor correspondiente es 1 − 1 = 0. Al expandir el producto en el lado izquierdo, se obtiene la ecuación ( 4 ).

Para probar el principio de inclusión-exclusión para la cardinalidad de conjuntos, sume la ecuación ( 4 ) sobre todo x en la unión de A ₁ ,…, An _. Para derivar la versión utilizada en probabilidad, tome la expectativa en ( 4 ). En general, integre la ecuación ( 4 ) con respecto a  μ . Utilice siempre la linealidad en estas derivaciones.

Ver también

• Desigualdad de Boole  : desigualdad aplicada a espacios de probabilidad
• Principios combinatorios  : métodos utilizados en combinatoria.
• Identidad máximo-mínimo  : relaciona el elemento máximo de un conjunto de números y los mínimos de sus subconjuntos no vacíos.
• Problema con el collar
• Principio de casillero  : si hay más artículos que cajas que los contienen, una caja debe contener al menos dos artículos
• Fórmula de Schuette-Nesbitt  : fórmula matemática en teoría de la probabilidadPages displaying wikidata descriptions as a fallback

Notas

1. Roberts y Tesman 2009, pág. 405
2. Mazur 2010, pág. 94
3. van Lint y Wilson 1992, pág. 77
4. van Lint y Wilson 1992, pág. 77
5. Stanley 1986, pág. 64
6. Rota, Gian-Carlo (1964), "Sobre los fundamentos de la teoría combinatoria I. Teoría de las funciones de Möbius", Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete , 2 (4): 340–368, doi : 10.1007/BF00531932 , S2CID  121334025
7. Brualdi 2010, págs. 167–8
8. Cameron 1994, pág. 78
9. Graham, Grötschel y Lovász 1995, pág. 1049
10. van Lint y Wilson 1992, págs.77-8
11. Björklund, Husfeldt y Koivisto 2009
12. Bruto 2008, págs. 211-13
13. Bruto 2008, págs. 208-10
14. Mazur 2010, págs. 84-5, 90
15. Brualdi 2010, págs. 177–81
16. Brualdi 2010, págs. 282–7
17. Roberts y Tesman 2009, páginas 419-20
18. van Lint y Wilson 1992, pág. 73
19. (Fernández, Fröhlich & Alan D. 1992, Proposición 12.6)

Referencias

• Allenby, RBJT; Slomson, Alan (2010), Cómo contar: una introducción a la combinatoria, las matemáticas discretas y sus aplicaciones (2 ed.), CRC Press, págs. 51–60, ISBN 9781420082609
• Björklund, A.; Husfeldt, T.; Koivisto, M. (2009), "Establecer partición mediante inclusión-exclusión", SIAM Journal on Computing , 39 (2): 546–563, CiteSeerX  10.1.1.526.9573 , doi :10.1137/070683933
• Brualdi, Richard A. (2010), Combinatoria introductoria (5ª ed.), Prentice – Hall, ISBN 9780136020400
• Cameron, Peter J. (1994), Combinatoria: temas, técnicas, algoritmos , Cambridge University Press, ISBN 0-521-45761-0
• Fernández, Roberto; Fröhlich, Jürg ; Alan D., Sokal (1992), Paseos aleatorios, fenómenos críticos y trivialidad en la teoría cuántica de campos , Textos y monografías de física, Berlín: Springer-Verlag , págs. xviii+444, ISBN 3-540-54358-9, SEÑOR  1219313, Zbl  0761.60061
• Graham, RL; Grötschel, M .; Lovász, L. (1995), Manual de combinatoria (volumen 2) , MIT Press - Holanda Septentrional, ISBN 9780262071710
• Gross, Jonathan L. (2008), Métodos combinatorios con aplicaciones informáticas , Chapman&Hall/CRC, ISBN 9781584887430
• "Principio de inclusión y exclusión", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Mazur, David R. (2010), Combinatoria: una visita guiada , Asociación Matemática de América, ISBN 9780883857625
• Roberts, Fred S.; Tesman, Barry (2009), Combinatoria aplicada (2ª ed.), CRC Press, ISBN 9781420099829
• Stanley, Richard P. (1986), Combinatoria enumerativa Volumen I , Wadsworth & Brooks/Cole, ISBN 0534065465
• van Lint, JH; Wilson, RM (1992), Un curso de combinatoria , Cambridge University Press, ISBN 0521422604

Este artículo incorpora material del principio de inclusión-exclusión en PlanetMath , que tiene la licencia Creative Commons Attribution/Share-Alike License .