Grupo Coxeter

Grupo que admite una descripción formal en términos de reflexiones

En matemáticas , un grupo de Coxeter , llamado así por HSM Coxeter , es un grupo abstracto que admite una descripción formal en términos de reflexiones (o espejos caleidoscópicos ). En efecto, los grupos de Coxeter finitos son precisamente los grupos de reflexión euclidianos finitos ; por ejemplo, el grupo de simetría de cada poliedro regular es un grupo de Coxeter finito. Sin embargo, no todos los grupos de Coxeter son finitos, y no todos pueden describirse en términos de simetrías y reflexiones euclidianas. Los grupos de Coxeter se introdujeron en 1934 como abstracciones de los grupos de reflexión, ^[1] y los grupos de Coxeter finitos se clasificaron en 1935. ^[2]

Los grupos de Coxeter encuentran aplicaciones en muchas áreas de las matemáticas. Ejemplos de grupos de Coxeter finitos incluyen los grupos de simetría de politopos regulares y los grupos de Weyl de álgebras de Lie simples . Ejemplos de grupos de Coxeter infinitos incluyen los grupos de triángulos correspondientes a teselaciones regulares del plano euclidiano y el plano hiperbólico , y los grupos de Weyl de álgebras de Kac-Moody de dimensión infinita . ^{[3] [4] [5]}

Definición

Formalmente, un grupo de Coxeter se puede definir como un grupo con la presentación

${\displaystyle \left\langle r_{1},r_{2},\ldots ,r_{n}\mid (r_{i}r_{j})^{m_{ij}}=1\right\rangle }$

donde y es un entero o para . Aquí, la condición significa que no se debe imponer ninguna relación de la forma para ningún entero . ${\displaystyle m_{ii}=1}$ ${\displaystyle m_{ij}=m_{ji}\geq 2}$ ${\displaystyle \infty }$ ${\displaystyle i\neq j}$ ${\displaystyle m_{ij}=\infty }$ ${\displaystyle (r_{i}r_{j})^{m}=1}$ ${\displaystyle m\geq 2}$

El par donde es un grupo de Coxeter con generadores se llama sistema de Coxeter . Nótese que en general no está determinado de forma única por . Por ejemplo, los grupos de Coxeter de tipo y son isomorfos pero los sistemas de Coxeter no son equivalentes, ya que el primero tiene 3 generadores y el segundo tiene 1 + 3 = 4 generadores (ver más abajo una explicación de esta notación). ${\displaystyle (W,S)}$ ${\displaystyle W}$ ${\displaystyle S=\{r_{1},\dots ,r_{n}\}}$ ${\displaystyle S}$ ${\displaystyle W}$ ${\displaystyle B_{3}}$ ${\displaystyle A_{1}\times A_{3}}$

De la definición anterior se pueden extraer inmediatamente varias conclusiones.

• La relación significa que para todos  ; como tal los generadores son involuciones . ${\displaystyle m_{ii}=1}$ ${\displaystyle (r_{i}r_{i})^{1}=(r_{i})^{2}=1}$ ${\displaystyle i}$
• Si , entonces los generadores y conmutan. Esto se deduce de la observación de que ${\displaystyle m_{ij}=2}$ ${\displaystyle r_{i}}$ ${\displaystyle r_{j}}$

${\displaystyle xx=yy=1}$,

junto con

${\displaystyle xyxy=1}$

implica que

${\displaystyle xy=x(xyxy)y=(xx)yx(yy)=yx}$.

Alternativamente, dado que los generadores son involuciones, , entonces . Es decir, el conmutador de y es igual a 1, o equivalentemente que y conmutan. ${\displaystyle r_{i}=r_{i}^{-1}}$ ${\displaystyle 1=(r_{i}r_{j})^{2}=r_{i}r_{j}r_{i}r_{j}=r_{i}r_{j}r_{i}^{-1}r_{j}^{-1}}$ ${\displaystyle r_{i}}$ ${\displaystyle r_{j}}$ ${\displaystyle r_{i}}$ ${\displaystyle r_{j}}$

La razón por la que se estipula en la definición es que ${\displaystyle m_{ij}=m_{ji}}$ ${\displaystyle i\neq j}$

${\displaystyle yy=1}$,

junto con

${\displaystyle (xy)^{m}=1}$

ya implica que

${\displaystyle (yx)^{m}=(yx)^{m}yy=y(xy)^{m}y=yy=1}$.

Una prueba alternativa de esta implicación es la observación de que y son conjugados : de hecho . ${\displaystyle (xy)^{k}}$ ${\displaystyle (yx)^{k}}$ ${\displaystyle y(xy)^{k}y^{-1}=(yx)^{k}yy^{-1}=(yx)^{k}}$

Matriz de Coxeter y matriz de Schläfli

La matriz de Coxeter es la matriz simétrica con entradas . De hecho, toda matriz simétrica con entradas diagonales exclusivamente 1 y entradas no diagonales en el conjunto es una matriz de Coxeter. ${\displaystyle n\times n}$ ${\displaystyle m_{ij}}$ ${\displaystyle \{2,3,\ldots \}\cup \{\infty \}}$

La matriz de Coxeter se puede codificar convenientemente mediante un diagrama de Coxeter , según las siguientes reglas.

• Los vértices del gráfico están etiquetados mediante subíndices generadores.
• Los vértices y son adyacentes si y sólo si . ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle m_{ij}\geq 3}$
• Un borde se etiqueta con el valor de siempre que el valor sea o mayor. ${\displaystyle m_{ij}}$ ${\displaystyle 4}$

En particular, dos generadores conmutan si y solo si no están unidos por una arista. Además, si un grafo de Coxeter tiene dos o más componentes conectados , el grupo asociado es el producto directo de los grupos asociados a los componentes individuales. Por lo tanto, la unión disjunta de grafos de Coxeter produce un producto directo de grupos de Coxeter.

La matriz de Coxeter, , está relacionada con la matriz de Schläfli con elementos , pero los elementos se modifican, siendo proporcionales al producto escalar de los generadores por pares. La matriz de Schläfli es útil porque sus valores propios determinan si el grupo de Coxeter es de tipo finito (todos positivos), tipo afín (todos no negativos, al menos un cero) o tipo indefinido (de lo contrario). El tipo indefinido a veces se subdivide aún más, por ejemplo, en grupos de Coxeter hiperbólicos y otros. Sin embargo, existen múltiples definiciones no equivalentes para los grupos de Coxeter hiperbólicos. ${\displaystyle M_{ij}}$ ${\displaystyle n\times n}$ ${\displaystyle C}$ ${\displaystyle C_{ij}=-2\cos(\pi /M_{ij})}$

Un ejemplo

El gráfico en el que los vértices a través de se colocan en una fila con cada vértice unido por una arista no etiquetada a sus vecinos inmediatos es el diagrama de Coxeter del grupo simétrico ; los generadores corresponden a las transposiciones . Dos transposiciones no consecutivas cualesquiera conmutan, mientras que multiplicar dos transposiciones consecutivas da un 3-ciclo : . Por lo tanto es un cociente del grupo de Coxeter que tiene diagrama de Coxeter . Argumentos adicionales muestran que este mapa de cocientes es un isomorfismo. ${\displaystyle A_{n}}$ ${\displaystyle 1}$ ${\displaystyle n}$ ${\displaystyle S_{n+1}}$ ${\displaystyle (1~~2),(2~~3),\dots ,(n~~n+1)}$ ${\displaystyle (k~~k+1)\cdot (k+1~~k+2)=(k~~k+2~~k+1)}$ ${\displaystyle S_{n+1}}$ ${\displaystyle A_{n}}$

Abstracción de grupos de reflexión

Los grupos de Coxeter son una abstracción de los grupos de reflexión. Los grupos de Coxeter son grupos abstractos , en el sentido de que se dan mediante una presentación. Por otro lado, los grupos de reflexión son concretos , en el sentido de que cada uno de sus elementos es el compuesto de un número finito de reflexiones geométricas sobre hiperplanos lineales en algún espacio euclidiano. Técnicamente, un grupo de reflexión es un subgrupo de un grupo lineal (o varias generalizaciones) generado por matrices ortogonales de determinante -1. Cada generador de un grupo de Coxeter tiene orden 2, lo que abstrae el hecho geométrico de que realizar una reflexión dos veces es la identidad. Cada relación de la forma , correspondiente al hecho geométrico de que, dados dos hiperplanos que se encuentran en un ángulo de , el compuesto de las dos reflexiones sobre estos hiperplanos es una rotación de , que tiene orden k . ${\displaystyle (r_{i}r_{j})^{k}}$ ${\displaystyle \pi /k}$ ${\displaystyle 2\pi /k}$

De esta manera, cada grupo de reflexión puede presentarse como un grupo de Coxeter. ^[1] La inversa es parcialmente cierta: cada grupo de Coxeter finito admite una representación fiel como un grupo de reflexión finito de algún espacio euclidiano. ^[2] Sin embargo, no todo grupo de Coxeter infinito admite una representación como un grupo de reflexión.

Se han clasificado grupos de Coxeter finitos. ^[2]

Grupos de Coxeter finitos

Gráficas de Coxeter de los grupos de Coxeter finitos irreducibles

Clasificación

Los grupos de Coxeter finitos se clasifican en términos de sus diagramas de Coxeter . ^[2]

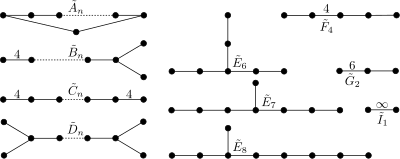
Los grupos de Coxeter finitos con diagramas de Coxeter conexos constan de tres familias de un parámetro de dimensión creciente ( para , para , y para ), una familia de un parámetro de dimensión dos ( para ), y seis grupos excepcionales ( y ). Cada grupo de Coxeter finito es el producto directo de un número finito de estos grupos irreducibles. ^[a] ${\displaystyle A_{n}}$ ${\displaystyle n\geq 1}$ ${\displaystyle B_{n}}$ ${\displaystyle n\geq 2}$ ${\displaystyle D_{n}}$ ${\displaystyle n\geq 4}$ ${\displaystyle I_{2}(p)}$ ${\displaystyle p\geq 5}$ ${\displaystyle E_{6},E_{7},E_{8},F_{4},H_{3},}$ ${\displaystyle H_{4}}$

Grupos de Weyl

Muchos de ellos, pero no todos, son grupos de Weyl, y cada grupo de Weyl puede realizarse como un grupo de Coxeter. Los grupos de Weyl son las familias y las excepciones y se denotan en la notación de grupos de Weyl como ${\displaystyle A_{n},B_{n},}$ ${\displaystyle D_{n},}$ ${\displaystyle E_{6},E_{7},E_{8},F_{4},}$ ${\displaystyle I_{2}(6),}$ ${\displaystyle G_{2}.}$

Los que no son de Weyl son las excepciones y aquellos miembros de la familia que no son excepcionalmente isomorfos a un grupo de Weyl (a saber, y ). ${\displaystyle H_{3}}$ ${\displaystyle H_{4},}$ ${\displaystyle I_{2}(p)}$ ${\displaystyle I_{2}(3)\cong A_{2},I_{2}(4)\cong B_{2},}$ ${\displaystyle I_{2}(6)\cong G_{2}}$

Esto se puede demostrar comparando las restricciones de los diagramas de Dynkin (no dirigidos) con las restricciones de los diagramas de Coxeter de grupos finitos: formalmente, el gráfico de Coxeter se puede obtener del diagrama de Dynkin descartando la dirección de las aristas y reemplazando cada arista doble con una arista etiquetada 4 y cada arista triple con una arista etiquetada 6. Nótese también que cada grupo de Coxeter generado finitamente es un grupo automático . ^[6] Los diagramas de Dynkin tienen la restricción adicional de que las únicas etiquetas de arista permitidas son 2, 3, 4 y 6, lo que produce lo anterior. Geométricamente, esto corresponde al teorema de restricción cristalográfica y al hecho de que los politopos excluidos no llenan el espacio ni teselan el plano –para el dodecaedro (dualmente, icosaedro) no llena el espacio; para el de 120 celdas (dualmente, 600 celdas) no llena el espacio; porque un p -gono no tesela el plano excepto para o (las teselaciones triangular, cuadrada y hexagonal, respectivamente). ${\displaystyle H_{3},}$ ${\displaystyle H_{4},}$ ${\displaystyle I_{2}(p)}$ ${\displaystyle p=3,4,}$ ${\displaystyle 6}$

Nótese además que los diagramas de Dynkin (dirigidos) B _n y C _n dan lugar al mismo grupo de Weyl (de ahí el grupo de Coxeter), porque difieren como gráficos dirigidos , pero concuerdan como gráficos no dirigidos – la dirección es importante para los sistemas raíz pero no para el grupo de Weyl; esto corresponde a que el hipercubo y el politopo cruzado son politopos regulares diferentes pero tienen el mismo grupo de simetría.

Propiedades

En la siguiente tabla se dan algunas propiedades de los grupos de Coxeter irreducibles finitos. El orden de un grupo reducible se puede calcular mediante el producto de los órdenes de sus subgrupos irreducibles.

Grupos de simetría de politopos regulares

El grupo de simetría de cada politopo regular es un grupo de Coxeter finito. Nótese que los politopos duales tienen el mismo grupo de simetría.

Existen tres series de politopos regulares en todas las dimensiones. El grupo de simetría de un n -símplex regular es el grupo simétrico S _{n +1} , también conocido como grupo de Coxeter de tipo A _n . El grupo de simetría del n - cubo y su dual, el n -politopo cruzado, es B _n , y se conoce como grupo hiperoctaédrico .

Los politopos regulares excepcionales en dimensiones dos, tres y cuatro corresponden a otros grupos de Coxeter. En dos dimensiones, los grupos diedros , que son los grupos de simetría de los polígonos regulares , forman la serie I ₂ ( p ), para p ≥ 3. En tres dimensiones, el grupo de simetría del dodecaedro regular y su dual, el icosaedro regular , es H ₃ , conocido como el grupo icosaédrico completo . En cuatro dimensiones, hay tres politopos regulares excepcionales, el de 24 celdas , el de 120 celdas y el de 600 celdas . El primero tiene grupo de simetría F ₄ , mientras que los otros dos son duales y tienen grupo de simetría H ₄ .

Los grupos de Coxeter de tipo D _n , E ₆ , E ₇ y E ₈ son los grupos de simetría de ciertos politopos semirregulares .

Grupos de Coxeter afines

Diagramas de Coxeter para los grupos de Coxeter afines

Diagrama de Stiefel para el sistema de raíces ${\displaystyle G_{2}}$

Los grupos de Coxeter afines forman una segunda serie importante de grupos de Coxeter. Estos no son finitos en sí mismos, pero cada uno contiene un subgrupo abeliano normal tal que el grupo cociente correspondiente es finito. En cada caso, el grupo cociente es en sí mismo un grupo de Coxeter, y el grafo de Coxeter del grupo de Coxeter afín se obtiene a partir del grafo de Coxeter del grupo cociente añadiendo otro vértice y una o dos aristas adicionales. Por ejemplo, para n  ≥ 2, el grafo que consiste en n +1 vértices en un círculo se obtiene de A _n de esta manera, y el grupo de Coxeter correspondiente es el grupo de Weyl afín de A _n (el grupo simétrico afín ). Para n  = 2, esto se puede representar como un subgrupo del grupo de simetría de la teselación estándar del plano por triángulos equiláteros.

En general, dado un sistema de raíces, se puede construir el diagrama de Stiefel asociado , que consiste en los hiperplanos ortogonales a las raíces junto con ciertas traslaciones de estos hiperplanos. El grupo de Coxeter afín (o grupo de Weyl afín) es entonces el grupo generado por las reflexiones (afines) sobre todos los hiperplanos en el diagrama. ^[9] El diagrama de Stiefel divide el plano en infinitos componentes conectados llamados alcobas , y el grupo de Coxeter afín actúa libre y transitivamente sobre las alcobas, tal como el grupo de Weyl ordinario actúa libre y transitivamente sobre las cámaras de Weyl. La figura de la derecha ilustra el diagrama de Stiefel para el sistema de raíces. ${\displaystyle G_{2}}$

Supóngase que es un sistema de raíces irreducible de rango y sea una colección de raíces simples. Sea, también, la raíz más alta. Entonces el grupo de Coxeter afín se genera por las reflexiones ordinarias (lineales) sobre los hiperplanos perpendiculares a , junto con una reflexión afín sobre una traslación del hiperplano perpendicular a . El grafo de Coxeter para el grupo de Weyl afín es el diagrama de Coxeter-Dynkin para , junto con un nodo adicional asociado a . En este caso, se puede obtener una alcoba del diagrama de Stiefel tomando la cámara fundamental de Weyl y cortándola por una traslación del hiperplano perpendicular a . ^[10] ${\displaystyle R}$ ${\displaystyle r>1}$ ${\displaystyle \alpha _{1},\ldots ,\alpha _{r}}$ ${\displaystyle \alpha _{r+1}}$ ${\displaystyle \alpha _{1},\ldots ,\alpha _{r}}$ ${\displaystyle \alpha _{r+1}}$ ${\displaystyle R}$ ${\displaystyle \alpha _{r+1}}$ ${\displaystyle \alpha _{r+1}}$

A continuación se muestra una lista de los grupos de Coxeter afines:

El subíndice del símbolo del grupo es uno menos que el número de nodos en cada caso, ya que cada uno de estos grupos se obtuvo agregando un nodo al gráfico de un grupo finito.

Grupos hiperbólicos de Coxeter

Hay infinitos grupos de Coxeter hiperbólicos que describen grupos de reflexión en el espacio hiperbólico , incluidos en particular los grupos de triángulos hiperbólicos.

Grupos de Coxeter irreducibles

Se dice que un grupo de Coxeter es irreducible si su diagrama de Coxeter-Dynkin es conexo. Todo grupo de Coxeter es el producto directo de los grupos irreducibles que corresponden a los componentes de su diagrama de Coxeter-Dynkin.

Órdenes parciales

Una elección de generadores de reflexión da lugar a una función de longitud ℓ en un grupo de Coxeter, es decir, el número mínimo de usos de generadores necesarios para expresar un elemento de grupo; esta es precisamente la longitud en la métrica de palabras en el grafo de Cayley . Una expresión para v que utiliza generadores ℓ ( v ) es una palabra reducida . Por ejemplo, la permutación (13) en S ₃ tiene dos palabras reducidas, (12)(23)(12) y (23)(12)(23). La función define una función que generaliza la función de signos para el grupo simétrico. ${\displaystyle v\to (-1)^{\ell (v)}}$ ${\displaystyle G\to \{\pm 1\},}$

Utilizando palabras reducidas se pueden definir tres órdenes parciales en el grupo de Coxeter, el orden débil (derecha) , el orden absoluto y el orden Bruhat (nombrado por François Bruhat ). Un elemento v excede a un elemento u en el orden Bruhat si alguna (o equivalentemente, cualquier) palabra reducida para v contiene una palabra reducida para u como subcadena, donde se omiten algunas letras (en cualquier posición). En el orden débil, v  ≥  u si alguna palabra reducida para v contiene una palabra reducida para u como segmento inicial. De hecho, la longitud de la palabra lo convierte en un poset graduado . Los diagramas de Hasse correspondientes a estos órdenes son objetos de estudio y están relacionados con el gráfico de Cayley determinado por los generadores. El orden absoluto se define de forma análoga al orden débil, pero con un conjunto/alfabeto generador que consta de todos los conjugados de los generadores de Coxeter.

Por ejemplo, la permutación (1 2 3) en S ₃ tiene sólo una palabra reducida, (12)(23), por lo que cubre (12) y (23) en el orden Bruhat pero sólo cubre (12) en el orden débil.

Homología

Dado que un grupo de Coxeter se genera a partir de un número finito de elementos de orden 2, su abelianización es un 2-grupo abeliano elemental , es decir, es isomorfo a la suma directa de varias copias del grupo cíclico . Esto puede reformularse en términos del primer grupo de homología de . ${\displaystyle W}$ ${\displaystyle Z_{2}}$ ${\displaystyle W}$

El multiplicador de Schur , igual al segundo grupo de homología de , se calculó en (Ihara y Yokonuma 1965) para grupos de reflexión finitos y en (Yokonuma 1965) para grupos de reflexión afines, con una explicación más unificada dada en (Howlett 1988). En todos los casos, el multiplicador de Schur es también un 2-grupo abeliano elemental. Para cada familia infinita de grupos de Weyl finitos o afines, el rango de se estabiliza a medida que tiende al infinito. ${\displaystyle M(W)}$ ${\displaystyle W}$ ${\displaystyle \{W_{n}\}}$ ${\displaystyle M(W_{n})}$ ${\displaystyle n}$

Véase también

• Grupo Artin-Tits
• Teorema de Chevalley-Shephard-Todd
• Grupo de reflexión complejo
• Elemento de Coxeter
• Álgebra de Iwahori-Hecke , una deformación cuántica del álgebra de grupos
• Polinomio de Kazhdan-Lusztig
• Elemento más largo de un grupo de Coxeter
• Subgrupo parabólico de un grupo de reflexión
• Disposición supersoluble

Notas

1. En algunos contextos, el esquema de nombres puede ampliarse para permitir los siguientes nombres alternativos o redundantes: , , , , y . ${\displaystyle B_{1}\cong A_{1}}$ ${\displaystyle D_{2}\cong I_{2}(2)\cong A_{1}\times A_{1}}$ ${\displaystyle I_{2}(3)\cong A_{2}}$ ${\displaystyle I_{2}(4)\cong B_{2}}$ ${\displaystyle H_{2}\cong I_{2}(5)}$ ${\displaystyle D_{3}\cong A_{3}}$
2. un subgrupo de índice 2 de ${\displaystyle \operatorname {GO} _{4}^{+}(5)}$

Referencias

1. Coxeter, HSM (1934). "Grupos discretos generados por reflexiones". Anales de Matemáticas . 35 (3): 588–621. CiteSeerX  10.1.1.128.471 . doi :10.2307/1968753. JSTOR  1968753.
2. Coxeter, HSM (enero de 1935). "La enumeración completa de grupos finitos de la forma ". Journal of the London Mathematical Society : 21–25. doi :10.1112/jlms/s1-10.37.21. ${\displaystyle r_{i}^{2}=(r_{i}r_{j})^{k_{ij}}=1}$
3. Bourbaki, Nicolas (2002). "4-6". Grupos de Lie y álgebras de Lie . Elementos de matemáticas. Springer. ISBN 978-3-540-42650-9. Número de serie  0983.17001.
4. Humphreys, James E. (1990). Grupos de reflexión y grupos de Coxeter (PDF) . Cambridge Studies in Advanced Mathematics. Vol. 29. Cambridge University Press. doi :10.1017/CBO9780511623646. ISBN . 978-0-521-43613-7. Zbl  0725.20028 . Consultado el 18 de noviembre de 2023 .
5. Davis, Michael W. (2007). Geometría y topología de los grupos de Coxeter (PDF) . Princeton University Press. ISBN 978-0-691-13138-2. Zbl  1142.20020 . Consultado el 18 de noviembre de 2023 .
6. Brink, Brigitte; Howlett, Robert B. (1993). "Una propiedad de finitud y una estructura automática para grupos de Coxeter". Anales matemáticos . 296 (1): 179–190. doi :10.1007/BF01445101. S2CID  122177473. Zbl  0793.20036.
7. Coxeter, HSM (enero de 1973). "12.6. El número de reflexiones". Politopos regulares . Courier Corporation. ISBN 0-486-61480-8.
8. Wilson, Robert A. (2009), "Capítulo 2", Los grupos finitos simples , Graduate Texts in Mathematics 251, vol. 251, Berlín, Nueva York: Springer-Verlag , doi :10.1007/978-1-84800-988-2, ISBN 978-1-84800-987-5
9. Hall 2015 Sección 13.6
10. Hall 2015 Capítulo 13, Ejercicios 12 y 13

Bibliografía

• Hall, Brian C. (2015). Grupos de Lie, álgebras de Lie y representaciones: una introducción elemental . Textos de posgrado en matemáticas. Vol. 222 (2.ª ed.). Springer. ISBN 978-3-319-13466-6.
• Ihara, S.; Yokonuma, Takeo (1965). "Sobre los grupos de segunda cohomología (multiplicadores de Schur) de grupos de reflexión finitos" (PDF) . J. Fac. Sci. Univ. Tokio, Sect. 1 . 11 : 155–171. Zbl  0136.28802. Archivado desde el original (PDF) el 23 de octubre de 2013.
• Howlett, Robert B. (1988). "Sobre los multiplicadores de Schur de los grupos de Coxeter". J. London Math. Soc . 2. 38 (2): 263–276. doi :10.1112/jlms/s2-38.2.263. Zbl  0627.20019.
• Yokonuma, Takeo (1965). "Sobre los segundos grupos de cohomología (multiplicadores de Schur) de grupos de reflexión discretos infinitos". J. Fac. Sci. Univ. Tokio, Sect. 1 . 11 : 173–186. hdl :2261/6049. Zbl  0136.28803.

Lectura adicional

• Björner, Anders ; Brenti, Francesco (2005). Combinatoria de grupos de Coxeter. Textos de posgrado en matemáticas . Vol. 231. Springer. ISBN 978-3-540-27596-1.Zbl 1110.05001  .
• Grove, Larry C.; Benson, Clark T. (1985). Grupos de reflexión finitos. Textos de posgrado en matemáticas. Vol. 99. Springer. ISBN 978-0-387-96082-1.
• Kane, Richard (2001). Grupos de reflexión y teoría de invariantes. CMS Books in Mathematics. Springer. ISBN 978-0-387-98979-2.Zbl 0986.20038  .
• Hiller, Howard (1982). Geometría de los grupos de Coxeter. Notas de investigación en matemáticas. Vol. 54. Pitman. ISBN 978-0-273-08517-1.Zbl 0483.57002  .
• Vinberg, Ernest B. (1984). "Ausencia de grupos cristalográficos de reflexiones en espacios de Lobachevski de gran dimensión". Trudy Moskov. Mat. Obshch . 47 .

Enlaces externos

• "Grupo de Coxeter", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. , "Grupo Coxeter", MathWorld
• Software de Jenn para visualizar los gráficos de Cayley de grupos de Coxeter finitos en hasta cuatro generadores