Coeficiente de determinación

Indicador de qué tan bien los puntos de datos se ajustan a una línea o curva

Regresión de mínimos cuadrados ordinarios de la ley de Okun . Dado que la línea de regresión no deja pasar ningún punto por mucho, el R ² de la regresión es relativamente alto.

Comparación del estimador de Theil–Sen (negro) y la regresión lineal simple (azul) para un conjunto de puntos con valores atípicos . Debido a los numerosos valores atípicos, ninguna de las líneas de regresión se ajusta bien a los datos, como se mide por el hecho de que ninguna arroja un R ² muy alto .

En estadística , el coeficiente de determinación , denotado por ^R2 o r2 y pronunciado "R cuadrado", es la proporción de la variación en la variable dependiente que es predecible a partir de la ⁽ s) variable(s) independiente(s).

Es una estadística utilizada en el contexto de modelos estadísticos cuyo propósito principal es la predicción de resultados futuros o la prueba de hipótesis , sobre la base de otra información relacionada. Proporciona una medida de qué tan bien los resultados observados son replicados por el modelo, en función de la proporción de variación total de los resultados explicados por el modelo. ^{[1] [2] [3]}

Existen varias definiciones de R ² que sólo a veces son equivalentes. Una clase de tales casos incluye la regresión lineal simple donde se utiliza r ^{2 en lugar de} R ² . Cuando sólo se incluye una intersección , entonces r ² es simplemente el cuadrado del coeficiente de correlación de muestra (es decir, r ) entre los resultados observados y los valores predictores observados. ^[4] Si se incluyen regresores adicionales , R ² es el cuadrado del coeficiente de correlación múltiple . En ambos casos, el coeficiente de determinación normalmente varía de 0 a 1.

Existen casos en los que R ² puede producir valores negativos. Esto puede ocurrir cuando las predicciones que se comparan con los resultados correspondientes no se han derivado de un procedimiento de ajuste de modelos que utilice esos datos. Incluso si se ha utilizado un procedimiento de ajuste de modelos, R ² puede seguir siendo negativo, por ejemplo, cuando se realiza una regresión lineal sin incluir una intersección ^[5] o cuando se utiliza una función no lineal para ajustar los datos ^[6] . En los casos en los que surgen valores negativos, la media de los datos proporciona un mejor ajuste a los resultados que los valores de la función ajustada, según este criterio particular.

El coeficiente de determinación puede ser más intuitivamente informativo que MAE , MAPE , MSE y RMSE en la evaluación del análisis de regresión , ya que el primero se puede expresar como un porcentaje, mientras que las medidas del último tienen rangos arbitrarios. También demostró ser más robusto para ajustes deficientes en comparación con SMAPE en los conjuntos de datos de prueba del artículo. ^[7]

Al evaluar la bondad de ajuste de los valores simulados ( Y _pred ) versus los medidos ( Y _obs ), no es apropiado basarlo en el R ² de la regresión lineal (es decir, Y _obs = m · Y _pred + b). ^{[ cita requerida ]} El R ² cuantifica el grado de cualquier correlación lineal entre Y _obs e Y _pred , mientras que para la evaluación de bondad de ajuste solo se debe tomar en consideración una correlación lineal específica: Y _obs = 1 · Y _pred + 0 (es decir, la línea 1:1). ^{[8] [9]}

Definiciones

${\displaystyle R^{2}=1-{\frac {\color {blue}{SS_{\text{res}}}}{\color {red}{SS_{\text{tot}}}}}}$
Cuanto mejor se ajuste la regresión lineal (a la derecha) a los datos en comparación con el promedio simple (en el gráfico de la izquierda), más cercano será el valor de R ² a 1. Las áreas de los cuadrados azules representan los residuos al cuadrado con respecto a la regresión lineal. Las áreas de los cuadrados rojos representan los residuos al cuadrado con respecto al valor promedio.

Un conjunto de datos tiene n valores marcados y ₁ , ..., y _n (conocidos colectivamente como y _i o como un vector y = [ y ₁ , ..., y _n ] ^T ), cada uno asociado con un valor ajustado (o modelado, o predicho) f ₁ , ..., f _n (conocido como f _i , o a veces ŷ _i , como un vector f ).

Defina los residuos como e _i = y _i − f _i (formando un vector e ).

Si es la media de los datos observados: entonces la variabilidad del conjunto de datos se puede medir con dos fórmulas de suma de cuadrados : ${\displaystyle {\bar {y}}}$ $${\displaystyle {\bar {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$$

• La suma de los cuadrados de los residuos, también llamada suma de los cuadrados de los residuos : $${\displaystyle SS_{\text{res}}=\sum _{i}(y_{i}-f_{i})^{2}=\sum _{i}e_{i}^{2}\,}$$
• La suma total de cuadrados (proporcional a la varianza de los datos): $${\displaystyle SS_{\text{tot}}=\sum _{i}(y_{i}-{\bar {y}})^{2}}$$

La definición más general del coeficiente de determinación es $${\displaystyle R^{2}=1-{SS_{\rm {res}} \over SS_{\rm {tot}}}}$$

En el mejor de los casos, los valores modelados coinciden exactamente con los valores observados, lo que da como resultado y R ² = 1. Un modelo de referencia, que siempre predice y , tendrá R ² = 0 . ${\displaystyle SS_{\text{res}}=0}$

Relación con la varianza inexplicada

En una forma general, se puede ver que R ² está relacionado con la fracción de varianza no explicada (FVU), ya que el segundo término compara la varianza no explicada (varianza de los errores del modelo) con la varianza total (de los datos): $${\displaystyle R^{2}=1-{\text{FVU}}}$$

Como se explicó la varianza

Un valor mayor de R ² implica un modelo de regresión más exitoso. ^{[4] : 463} Supongamos que R ² = 0,49 . Esto implica que se ha tenido en cuenta el 49% de la variabilidad de la variable dependiente en el conjunto de datos, y el 51% restante de la variabilidad aún no se ha tenido en cuenta. Para los modelos de regresión, la suma de cuadrados de la regresión, también llamada suma de cuadrados explicada , se define como

${\displaystyle SS_{\text{reg}}=\sum _{i}(f_{i}-{\bar {y}})^{2}}$

En algunos casos, como en la regresión lineal simple , la suma total de cuadrados es igual a la suma de las otras dos sumas de cuadrados definidas anteriormente:

${\displaystyle SS_{\text{res}}+SS_{\text{reg}}=SS_{\text{tot}}}$

Consulte Particiones en el modelo MCO general para obtener una derivación de este resultado para un caso en el que se cumple la relación. Cuando esta relación se cumple, la definición anterior de R ² es equivalente a

${\displaystyle R^{2}={\frac {SS_{\text{reg}}}{SS_{\text{tot}}}}={\frac {SS_{\text{reg}}/n}{SS_{\text{tot}}/n}}}$

donde n es el número de observaciones (casos) sobre las variables.

En esta forma, R ² se expresa como la relación entre la varianza explicada (varianza de las predicciones del modelo, que es SS _reg / n ) y la varianza total (varianza muestral de la variable dependiente, que es SS _tot / n ).

Esta partición de la suma de cuadrados se cumple, por ejemplo, cuando los valores del modelo ƒ _i se han obtenido mediante regresión lineal . Una condición suficiente más suave se lee como sigue: El modelo tiene la forma

${\displaystyle f_{i}={\widehat {\alpha }}+{\widehat {\beta }}q_{i}}$

donde q _i son valores arbitrarios que pueden o no depender de i o de otros parámetros libres (la opción común q _i  =  x _i es sólo un caso especial), y las estimaciones de los coeficientes y se obtienen minimizando la suma residual de los cuadrados. ${\displaystyle {\widehat {\alpha }}}$ ${\displaystyle {\widehat {\beta }}}$

Este conjunto de condiciones es importante y tiene varias implicaciones para las propiedades de los residuos ajustados y los valores modelados. En particular, en estas condiciones:

${\displaystyle {\bar {f}}={\bar {y}}.\,}$

Como coeficiente de correlación al cuadrado

En la regresión múltiple de mínimos cuadrados lineal (con intersección y pendiente ajustadas), R ² es igual al cuadrado del coeficiente de correlación de Pearson entre los valores de datos observados y modelados (predichos) de la variable dependiente. ${\displaystyle \rho ^{2}(y,f)}$ ${\displaystyle y}$ ${\displaystyle f}$

En una regresión lineal de mínimos cuadrados con un solo explicador (con intersección y pendiente ajustadas), esto también es igual al cuadrado del coeficiente de correlación de Pearson entre la variable dependiente y la variable explicativa . ${\displaystyle \rho ^{2}(y,x)}$ ${\displaystyle y}$ ${\displaystyle x}$

No debe confundirse con el coeficiente de correlación entre dos variables explicativas , definido como

${\displaystyle \rho _{{\widehat {\alpha }},{\widehat {\beta }}}={\operatorname {cov} \left({\widehat {\alpha }},{\widehat {\beta }}\right) \over \sigma _{\widehat {\alpha }}\sigma _{\widehat {\beta }}},}$

donde la covarianza entre dos estimaciones de coeficientes, así como sus desviaciones estándar , se obtienen de la matriz de covarianza de las estimaciones de coeficientes, . ${\displaystyle (X^{T}X)^{-1}}$

En condiciones de modelado más generales, donde los valores predichos pueden generarse a partir de un modelo diferente de la regresión lineal de mínimos cuadrados, un valor R ² puede calcularse como el cuadrado del coeficiente de correlación entre los valores de datos originales y modelados . En este caso, el valor no es directamente una medida de cuán buenos son los valores modelados, sino más bien una medida de cuán bueno puede construirse un predictor a partir de los valores modelados (mediante la creación de un predictor revisado de la forma α + βƒ _i ). ^{[ cita requerida ]} Según Everitt, ^[10] este uso es específicamente la definición del término "coeficiente de determinación": el cuadrado de la correlación entre dos variables (generales). ${\displaystyle y}$ ${\displaystyle f}$

Interpretación

R ² es una medida de la bondad de ajuste de un modelo. ^[11] En regresión, el coeficiente de determinación R ^{2 es una medida estadística de qué tan bien las predicciones de regresión se aproximan a los puntos de datos reales. Un} R ² de 1 indica que las predicciones de regresión se ajustan perfectamente a los datos.

Los valores de R ² fuera del rango de 0 a 1 se producen cuando el modelo se ajusta a los datos peor que el peor predictor de mínimos cuadrados posible (equivalente a un hiperplano horizontal a una altura igual a la media de los datos observados). Esto ocurre cuando se eligió un modelo incorrecto o se aplicaron restricciones sin sentido por error. Si se utiliza la ecuación 1 de Kvålseth ^[12] (esta es la ecuación que se utiliza con más frecuencia), R ² puede ser menor que cero. Si se utiliza la ecuación 2 de Kvålseth, R ² puede ser mayor que uno.

En todos los casos en los que se utiliza R ² , los predictores se calculan mediante regresión de mínimos cuadrados ordinarios: es decir, minimizando SS _res . En este caso, R ² aumenta a medida que aumenta el número de variables en el modelo ( R ² es monótonamente creciente con el número de variables incluidas, nunca disminuirá). Esto ilustra un inconveniente de un posible uso de R ² , donde uno podría seguir añadiendo variables ( regresión del fregadero de la cocina ) para aumentar el valor de R ² . Por ejemplo, si uno está tratando de predecir las ventas de un modelo de automóvil a partir del consumo de gasolina, el precio y la potencia del motor del automóvil, puede incluir factores probablemente irrelevantes como la primera letra del nombre del modelo o la altura del ingeniero principal que diseña el automóvil porque R ² nunca disminuirá a medida que se agregan variables y probablemente experimentará un aumento debido solo al azar.

Esto nos lleva al enfoque alternativo de observar el R2 ajustado. La explicación de esta estadística es casi la misma que la del R2 ^, pero penaliza la estadística ya que se incluyen variables adicionales en el modelo. Para casos distintos del ajuste por mínimos cuadrados ordinarios, la ^estadística R2 se puede calcular como se indicó anteriormente y aún puede ser una medida útil. Si el ajuste se realiza por mínimos cuadrados ponderados o mínimos cuadrados generalizados , ^se pueden calcular versiones alternativas de R2 ^{adecuadas para esos marcos estadísticos, mientras que el} R2 "bruto" ^puede seguir siendo útil si se interpreta más fácilmente. Los valores de R2 se pueden calcular para cualquier tipo de modelo predictivo, que no necesita tener una base estadística.

En un modelo lineal múltiple

Considérese un modelo lineal con más de una variable explicativa , de la forma

${\displaystyle Y_{i}=\beta _{0}+\sum _{j=1}^{p}\beta _{j}X_{i,j}+\varepsilon _{i},}$

donde, para el i ésimo caso, es la variable de respuesta, son p regresores y es un término de error medio cero. Las cantidades son coeficientes desconocidos, cuyos valores se estiman por mínimos cuadrados . El coeficiente de determinación R ² es una medida del ajuste global del modelo. Específicamente, R ² es un elemento de [0, 1] y representa la proporción de variabilidad en Y _i que puede atribuirse a alguna combinación lineal de los regresores ( variables explicativas ) en X . ^[13] ${\displaystyle {Y_{i}}}$ ${\displaystyle X_{i,1},\dots ,X_{i,p}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle \beta _{0},\dots ,\beta _{p}}$

R ² se interpreta a menudo como la proporción de variación de respuesta "explicada" por los regresores en el modelo. Por lo tanto, R ²  = 1 indica que el modelo ajustado explica toda la variabilidad en , mientras que R ²  = 0 indica que no hay una relación "lineal" (para la regresión lineal, esto significa que el modelo lineal es una línea constante (pendiente = 0, intersección =  ) entre la variable de respuesta y los regresores). Un valor interior como R ²  = 0,7 puede interpretarse de la siguiente manera: "El setenta por ciento de la varianza en la variable de respuesta puede explicarse por las variables explicativas. El treinta por ciento restante puede atribuirse a variables desconocidas, latentes o variabilidad inherente". ${\displaystyle y}$ ${\displaystyle {\bar {y}}}$

Una advertencia que se aplica a R ² , al igual que a otras descripciones estadísticas de correlación y asociación, es que " la correlación no implica causalidad ". En otras palabras, si bien las correlaciones a veces pueden proporcionar pistas valiosas para descubrir relaciones causales entre variables, una correlación estimada distinta de cero entre dos variables no es, por sí sola, evidencia de que cambiar el valor de una variable daría como resultado cambios en los valores de otras variables. Por ejemplo, la práctica de llevar cerillas (o un encendedor) está correlacionada con la incidencia de cáncer de pulmón, pero llevar cerillas no causa cáncer (en el sentido estándar de "causa").

En el caso de un solo regresor, ajustado por mínimos cuadrados, R ² es el cuadrado del coeficiente de correlación producto-momento de Pearson que relaciona el regresor y la variable de respuesta. De manera más general, R ² es el cuadrado de la correlación entre el predictor construido y la variable de respuesta. Con más de un regresor, el R ² puede denominarse coeficiente de determinación múltiple .

Inflación deR2

En la regresión de mínimos cuadrados que utiliza datos típicos, R ² aumenta al menos débilmente con un aumento en el número de regresores en el modelo. Debido a que los aumentos en el número de regresores aumentan el valor de R ² , R ² por sí solo no puede usarse como una comparación significativa de modelos con números muy diferentes de variables independientes. Para una comparación significativa entre dos modelos, se puede realizar una prueba F en la suma residual de cuadrados ^{[ cita requerida ]} , similar a las pruebas F en la causalidad de Granger , aunque esto no siempre es apropiado ^{[ se necesita más explicación ]} . Como recordatorio de esto, algunos autores denotan R ² por R _q ² , donde q es el número de columnas en X (el número de explicadores incluyendo la constante).

Para demostrar esta propiedad, primero recordemos que el objetivo de la regresión lineal de mínimos cuadrados es

${\displaystyle \min _{b}SS_{\text{res}}(b)\Rightarrow \min _{b}\sum _{i}(y_{i}-X_{i}b)^{2}\,}$

donde X _i es un vector fila de valores de variables explicativas para el caso i y b es un vector columna de coeficientes de los respectivos elementos de X _i .

El valor óptimo del objetivo es débilmente menor a medida que se añaden más variables explicativas y, por lo tanto, se añaden columnas adicionales de (la matriz de datos explicativos cuya fila i es Xi ) _, por el hecho de que una minimización menos restringida conduce a un coste óptimo que es débilmente menor que una minimización más restringida. Dada la conclusión anterior y observando que depende solo de y , la propiedad no decreciente de R ² se desprende directamente de la definición anterior. ${\displaystyle X}$ ${\displaystyle SS_{tot}}$

La razón intuitiva por la que el uso de una variable explicativa adicional no puede reducir el R ² es la siguiente: minimizar es equivalente a maximizar el R ² . Cuando se incluye la variable adicional, los datos siempre tienen la opción de darle un coeficiente estimado de cero, dejando los valores predichos y el R ² sin cambios. La única forma en que el problema de optimización dará un coeficiente distinto de cero es si al hacerlo se mejora el  R ² . ${\displaystyle SS_{\text{res}}}$

Lo anterior ofrece una explicación analítica de la inflación de R ² . A continuación, se muestra un ejemplo basado en el método de mínimos cuadrados ordinarios desde una perspectiva geométrica. ^[14]

Este es un ejemplo de residuos de modelos de regresión en espacios más pequeños y más grandes basados ​​en la regresión de mínimos cuadrados ordinarios.

Consideremos primero un caso sencillo:

${\displaystyle Y=\beta _{0}+\beta _{1}\cdot X_{1}+\varepsilon \,}$

Esta ecuación describe el modelo de regresión de mínimos cuadrados ordinarios con un regresor. La predicción se muestra como el vector rojo en la figura de la derecha. Geométricamente, es la proyección del valor verdadero sobre un espacio del modelo en (sin intersección). El residuo se muestra como la línea roja. ${\displaystyle \mathbb {R} }$

${\displaystyle Y=\beta _{0}+\beta _{1}\cdot X_{1}+\beta _{2}\cdot X_{2}+\varepsilon \,}$

Esta ecuación corresponde al modelo de regresión de mínimos cuadrados ordinarios con dos regresores. La predicción se muestra como el vector azul en la figura de la derecha. Geométricamente, es la proyección del valor verdadero sobre un espacio de modelo más grande en (sin intersección). Cabe destacar que los valores de y no son los mismos que en la ecuación para un espacio de modelo más pequeño siempre que y no sean vectores cero. Por lo tanto, se espera que las ecuaciones produzcan predicciones diferentes (es decir, se espera que el vector azul sea diferente del vector rojo). El criterio de regresión de mínimos cuadrados garantiza que se minimice el residuo. En la figura, la línea azul que representa el residuo es ortogonal al espacio de modelo en , lo que da la distancia mínima desde el espacio. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$ ${\displaystyle \mathbb {R} ^{2}}$

El espacio del modelo más pequeño es un subespacio del más grande y, por lo tanto, se garantiza que el residuo del modelo más pequeño será mayor. Comparando las líneas roja y azul en la figura, la línea azul es ortogonal al espacio y cualquier otra línea sería mayor que la azul. Teniendo en cuenta el cálculo para R ² , un valor menor de conducirá a un valor mayor de R ² , lo que significa que agregar regresores dará como resultado una inflación de R ² . ${\displaystyle SS_{tot}}$

Advertencias

R ² no indica si:

• Las variables independientes son causa de los cambios en la variable dependiente ;
• existe sesgo de variable omitida ;
• Se utilizó la regresión correcta;
• Se ha elegido el conjunto más apropiado de variables independientes;
• Existe colinealidad presente en los datos de las variables explicativas;
• El modelo podría mejorarse utilizando versiones transformadas del conjunto existente de variables independientes;
• Hay suficientes puntos de datos para llegar a una conclusión sólida.

Extensiones

EquilibradoR2

El uso de un R ² ajustado (una notación común es , pronunciado "R barra al cuadrado"; otra es o ) es un intento de explicar el fenómeno del aumento automático del R ² cuando se añaden variables explicativas adicionales al modelo. Hay muchas formas diferentes de realizar el ajuste. ^[15] La más utilizada, hasta el punto de que normalmente se la denomina simplemente R 2 ajustado , es la corrección propuesta por Mordecai Ezekiel . ^{[15] [16] [17]} El R ² ajustado se define como ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle R_{\text{a}}^{2}}$ ${\displaystyle R_{\text{adj}}^{2}}$

${\displaystyle {\bar {R}}^{2}={1-{SS_{\text{res}}/{\text{df}}_{\text{res}} \over SS_{\text{tot}}/{\text{df}}_{\text{tot}}}}}$

donde df _res son los grados de libertad de la estimación de la varianza poblacional alrededor del modelo, y df _tot son los grados de libertad de la estimación de la varianza poblacional alrededor de la media. df _res se da en términos del tamaño de la muestra n y el número de variables p en el modelo, df _res = n − p − 1 . df _tot se da de la misma manera, pero con p siendo la unidad para la media, es decir, df _tot = n − 1 .

Insertando los grados de libertad y utilizando la definición de R ² , se puede reescribir como:

${\displaystyle {\bar {R}}^{2}=1-(1-R^{2}){n-1 \over n-p-1}}$

donde p es el número total de variables explicativas en el modelo (excluyendo la intersección) y n es el tamaño de la muestra.

El R ² ajustado puede ser negativo y su valor siempre será menor o igual que el de R ² . A diferencia de R ^{2 , el} R ² ajustado aumenta solo cuando el aumento de R ² (debido a la inclusión de una nueva variable explicativa) es mayor que el que se esperaría ver por casualidad. Si se introduce un conjunto de variables explicativas con una jerarquía de importancia predeterminada en una regresión una a la vez, y se calcula el R ^{2 ajustado cada vez, el nivel en el que} el R ² ajustado alcanza un máximo y luego disminuye, sería la regresión con la combinación ideal de tener el mejor ajuste sin términos excesivos o innecesarios.

Esquema de la contribución del sesgo y la varianza al error total

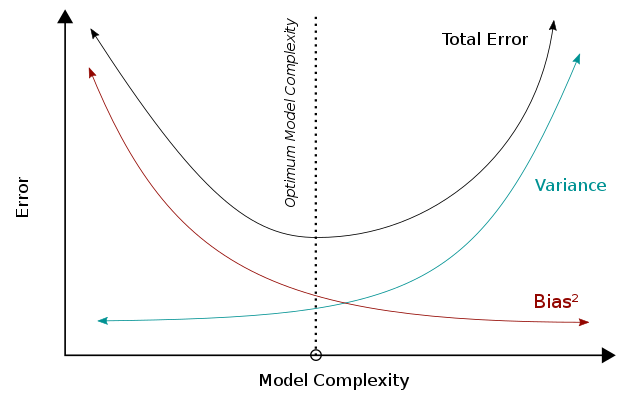
El R ² ajustado se puede interpretar como una instancia del equilibrio entre sesgo y varianza . Cuando consideramos el desempeño de un modelo, un error menor representa un mejor desempeño. Cuando el modelo se vuelve más complejo, la varianza aumentará mientras que el cuadrado del sesgo disminuirá, y estas dos métricas se suman para formar el error total. Combinando estas dos tendencias, el equilibrio entre sesgo y varianza describe una relación entre el desempeño del modelo y su complejidad, que se muestra como una curva en forma de U a la derecha. Para el R ² ajustado específicamente, la complejidad del modelo (es decir, el número de parámetros) afecta al R ² y al término / frac y, por lo tanto, captura sus atributos en el desempeño general del modelo.

R ² se puede interpretar como la varianza del modelo, que está influenciada por la complejidad del modelo. Un R ² alto indica un error de sesgo menor porque el modelo puede explicar mejor el cambio de Y con predictores. Por esta razón, hacemos menos suposiciones (erróneas), y esto resulta en un error de sesgo menor. Mientras tanto, para dar cabida a menos suposiciones, el modelo tiende a ser más complejo. Con base en el equilibrio entre sesgo y varianza, una mayor complejidad conducirá a una disminución del sesgo y un mejor rendimiento (por debajo de la línea óptima). En R ² , el término ( 1 − R ² ) será menor con una alta complejidad y dará como resultado un R ² mayor , lo que indica consistentemente un mejor rendimiento.

Por otro lado, el término/frac término se ve afectado de manera inversa por la complejidad del modelo. El término/frac término aumentará al agregar regresores (es decir, aumentará la complejidad del modelo) y conducirá a un peor desempeño. Según el equilibrio entre sesgo y varianza, una mayor complejidad del modelo (más allá de la línea óptima) conduce a un aumento de errores y a un peor desempeño.

Teniendo en cuenta el cálculo de R ² , más parámetros aumentarán el R ² y conducirán a un aumento en R ² . Sin embargo, agregar más parámetros aumentará el término/frac y, por lo tanto, disminuirá R ² . Estas dos tendencias construyen una relación en forma de U inversa entre la complejidad del modelo y R ² , que es consistente con la tendencia en forma de U de la complejidad del modelo versus el rendimiento general. A diferencia de R ² , que siempre aumentará cuando aumenta la complejidad del modelo, R ² aumentará solo cuando el sesgo eliminado por el regresor agregado sea mayor que la varianza introducida simultáneamente. El uso de R ² en lugar de R ² podría evitar el sobreajuste.

Siguiendo la misma lógica, el R ² ajustado puede interpretarse como un estimador menos sesgado del R ² de la población , mientras que el R ² de la muestra observada es una estimación positivamente sesgada del valor de la población. ^[18] El R ² ajustado es más apropiado cuando se evalúa el ajuste del modelo (la varianza en la variable dependiente explicada por las variables independientes) y al comparar modelos alternativos en la etapa de selección de características de la construcción del modelo. ^[18]

El principio detrás de la estadística R ² ajustada se puede ver reescribiendo el R ² ordinario como

${\displaystyle R^{2}={1-{{\text{VAR}}_{\text{res}} \over {\text{VAR}}_{\text{tot}}}}}$

donde y son las varianzas muestrales de los residuos estimados y de la variable dependiente respectivamente, que pueden considerarse estimaciones sesgadas de las varianzas poblacionales de los errores y de la variable dependiente. Estas estimaciones se reemplazan por versiones estadísticamente no sesgadas : y . ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/n}$ ${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/n}$ ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/(n-p)}$ ${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/(n-1)}$

A pesar de utilizar estimadores insesgados para las varianzas poblacionales del error y la variable dependiente, el R ² ajustado no es un estimador insesgado del R ² poblacional , ^[18] lo que resulta de utilizar las varianzas poblacionales de los errores y la variable dependiente en lugar de estimarlas. Ingram Olkin y John W. Pratt derivaron el estimador insesgado de varianza mínima para el R ² poblacional , ^[19] que se conoce como estimador de Olkin-Pratt. Las comparaciones de diferentes enfoques para ajustar el R ² concluyeron que en la mayoría de las situaciones se debería preferir una versión aproximada del estimador de Olkin-Pratt ^[18] o el estimador exacto de Olkin-Pratt ^{[20] sobre} el R ² ajustado (Ezequiel) .

Coeficiente de determinación parcial

El coeficiente de determinación parcial se puede definir como la proporción de variación que no se puede explicar en un modelo reducido, pero que se puede explicar mediante los predictores especificados en un modelo más completo. ^{[21] [22] [23]} Este coeficiente se utiliza para proporcionar información sobre si uno o más predictores adicionales pueden ser útiles en un modelo de regresión más completamente especificado.

El cálculo del R ² parcial es relativamente sencillo después de estimar dos modelos y generar las tablas ANOVA para ellos. El cálculo del R ² parcial es

${\displaystyle {\frac {SS_{\text{ res, reduced}}-SS_{\text{ res, full}}}{SS_{\text{ res, reduced}}}},}$

que es análogo al coeficiente de determinación habitual:

${\displaystyle {\frac {SS_{\text{tot}}-SS_{\text{res}}}{SS_{\text{tot}}}}.}$

Generalizando y descomponiendoR2

Como se explicó anteriormente, las heurísticas de selección de modelos, como el criterio R ² ajustado y la prueba F, examinan si el R ² total aumenta lo suficiente para determinar si se debe agregar un nuevo regresor al modelo. Si se agrega un regresor al modelo que está altamente correlacionado con otros regresores que ya se han incluido, entonces el R ² total apenas aumentará, incluso si el nuevo regresor es relevante. Como resultado, las heurísticas mencionadas anteriormente ignorarán los regresores relevantes cuando las correlaciones cruzadas sean altas. ^[24]

Representación geométrica de r ² .

Alternativamente, se puede descomponer una versión generalizada de R ² para cuantificar la relevancia de desviarse de una hipótesis. ^[24] Como muestra Hoornweg (2018), varios estimadores de contracción , como la regresión lineal bayesiana , la regresión de cresta y el lazo (adaptativo) , hacen uso de esta descomposición de R ² cuando reducen gradualmente los parámetros de las soluciones MCO sin restricciones hacia los valores hipotéticos. Definamos primero el modelo de regresión lineal como

${\displaystyle y=X\beta +\varepsilon .}$

Se supone que la matriz X está estandarizada con puntuaciones Z y que el vector columna está centrado para tener una media de cero. Supongamos que el vector columna hace referencia a los parámetros de regresión hipotéticos y que el vector columna denota los parámetros estimados. Podemos entonces definir ${\displaystyle y}$ ${\displaystyle \beta _{0}}$ ${\displaystyle b}$

${\displaystyle R^{2}=1-{\frac {(y-Xb)'(y-Xb)}{(y-X\beta _{0})'(y-X\beta _{0})}}.}$

Un R ² del 75 % significa que la precisión en la muestra mejora en un 75 % si se utilizan las soluciones b optimizadas para los datos en lugar de los valores hipotéticos. En el caso especial de que se trate de un vector de ceros, obtenemos nuevamente el R ² tradicional . ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{0}}$

El efecto individual sobre R ² de desviarse de una hipótesis se puede calcular con ('R-outer'). Esta matriz de tiempos está dada por ${\displaystyle R^{\otimes }}$ ${\displaystyle p}$ ${\displaystyle p}$

${\displaystyle R^{\otimes }=(X'{\tilde {y}}_{0})(X'{\tilde {y}}_{0})'(X'X)^{-1}({\tilde {y}}_{0}'{\tilde {y}}_{0})^{-1},}$

donde . Los elementos diagonales de suman exactamente R ² . Si los regresores no están correlacionados y es un vector de ceros, entonces el elemento diagonal de simplemente corresponde al valor r ² entre y . Cuando los regresores y están correlacionados, podría aumentar a costa de una disminución en . Como resultado, los elementos diagonales de pueden ser menores que 0 y, en casos más excepcionales, mayores que 1. Para lidiar con tales incertidumbres, varios estimadores de contracción toman implícitamente un promedio ponderado de los elementos diagonales de para cuantificar la relevancia de desviarse de un valor hipotético. ^[24] Haga clic en el lazo para ver un ejemplo. ${\displaystyle {\tilde {y}}_{0}=y-X\beta _{0}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle \beta _{0}}$ ${\displaystyle j^{\text{th}}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle x_{j}}$ ${\displaystyle y}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle R_{ii}^{\otimes }}$ ${\displaystyle R_{jj}^{\otimes }}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle R^{\otimes }}$

R2en regresión logística

En el caso de la regresión logística , generalmente ajustada por máxima verosimilitud , existen varias opciones de pseudo- R ² .

Una es la R ² generalizada propuesta originalmente por Cox y Snell, ^[25] e independientemente por Magee: ^[26]

${\displaystyle R^{2}=1-\left({{\mathcal {L}}(0) \over {\mathcal {L}}({\widehat {\theta }})}\right)^{2/n}}$

donde es la probabilidad del modelo con solo la intersección, es la probabilidad del modelo estimado (es decir, el modelo con un conjunto dado de estimaciones de parámetros) y n es el tamaño de la muestra. Se puede reescribir fácilmente como: ${\displaystyle {\mathcal {L}}(0)}$ ${\displaystyle {{\mathcal {L}}({\widehat {\theta }})}}$

${\displaystyle R^{2}=1-e^{{\frac {2}{n}}(\ln({\mathcal {L}}(0))-\ln({\mathcal {L}}({\widehat {\theta }}))}=1-e^{-D/n}}$

donde D es la estadística de prueba de la prueba de razón de verosimilitud .

Nico Nagelkerke señaló que tenía las siguientes propiedades: ^{[27] [22]}

1. Es consistente con el coeficiente de determinación clásico cuando ambos pueden calcularse;
2. Su valor se maximiza mediante la estimación de máxima verosimilitud de un modelo;
3. Es asintóticamente independiente del tamaño de la muestra;
4. La interpretación es la proporción de la variación explicada por el modelo;
5. Los valores están entre 0 y 1, donde 0 indica que el modelo no explica ninguna variación y 1 indica que explica perfectamente la variación observada;
6. No tiene ninguna unidad.

Sin embargo, en el caso de un modelo logístico, donde no puede ser mayor que 1, R ² está entre 0 y : por lo tanto, Nagelkerke sugirió la posibilidad de definir un R ² escalado como R ² / R ² _máx . ^[22] ${\displaystyle {\mathcal {L}}({\widehat {\theta }})}$ ${\displaystyle R_{\max }^{2}=1-({\mathcal {L}}(0))^{2/n}}$

Comparación con la norma de residuos

Ocasionalmente, se utiliza la norma de los residuos para indicar la bondad del ajuste. Este término se calcula como la raíz cuadrada de la suma de los cuadrados de los residuos :

${\displaystyle {\text{norm of residuals}}={\sqrt {SS_{\text{res}}}}=\|e\|.}$

Tanto R ² como la norma de los residuos tienen sus méritos relativos. Para el análisis de mínimos cuadrados, R ² varía entre 0 y 1, donde los números más grandes indican mejores ajustes y 1 representa un ajuste perfecto. La norma de los residuos varía de 0 a infinito, donde los números más pequeños indican mejores ajustes y cero indica un ajuste perfecto. Una ventaja y desventaja de R ² es que el término actúa para normalizar el valor. Si todos los valores y _i se multiplican por una constante, la norma de los residuos también cambiará por esa constante, pero R ² permanecerá igual. Como ejemplo básico, para el ajuste de mínimos cuadrados lineal al conjunto de datos: ${\displaystyle SS_{\text{tot}}}$

R ² = 0,998 y la norma de los residuos = 0,302. Si todos los valores de y se multiplican por 1000 (por ejemplo, en un cambio de prefijo del SI ), entonces R ² permanece igual, pero la norma de los residuos = 302.

Otro indicador de ajuste de un solo parámetro es el RMSE de los residuos, o la desviación estándar de los residuos. Este tendría un valor de 0,135 para el ejemplo anterior, dado que el ajuste fue lineal con una intersección no forzada. ^[28]

Historia

La creación del coeficiente de determinación se ha atribuido al genetista Sewall Wright y se publicó por primera vez en 1921. ^[29]

Véase también

• Cuarteto de Anscombe
• Fracción de varianza no explicada
• Bondad de ajuste
• Coeficiente de eficiencia del modelo de Nash-Sutcliffe ( aplicaciones hidrológicas )
• Coeficiente de correlación producto-momento de Pearson
• Reducción proporcional de la pérdida
• Validación del modelo de regresión
• Desviación cuadrática media
• Regresión por pasos

Notas

1. Steel, RGD; Torrie, JH (1960). Principios y procedimientos de estadística con especial referencia a las ciencias biológicas . McGraw Hill .
2. Glantz, Stanton A.; Slinker, BK (1990). Introducción a la regresión aplicada y al análisis de varianza . McGraw-Hill. ISBN 978-0-07-023407-9.
3. Draper, NR; Smith, H. (1998). Análisis de regresión aplicado . Wiley-Interscience. ISBN 978-0-471-17082-2.
4. Devore, Jay L. (2011). Probabilidad y estadística para ingeniería y ciencias (8.ª ed.). Boston, MA: Cengage Learning. págs. 508–510. ISBN 978-0-538-73352-6.
5. Barten, Anton P. (1987). "El coeficiente de determinación de la regresión sin término constante". En Heijmans, Risto; Neudecker, Heinz (eds.). La práctica de la econometría . Dordrecht: Kluwer. págs. 181–189. ISBN 90-247-3502-5.
6. Colin Cameron, A.; Windmeijer, Frank AG (1997). "Una medida R-cuadrada de bondad de ajuste para algunos modelos de regresión no lineal comunes". Journal of Econometrics . 77 (2): 1790–2. doi :10.1016/S0304-4076(96)01818-0.
7. Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). "El coeficiente de determinación R-cuadrado es más informativo que SMAPE, MAE, MAPE, MSE y RMSE en la evaluación del análisis de regresión". PeerJ Ciencias de la Computación . 7 (e623): e623. doi : 10.7717/peerj-cs.623 . PMC 8279135 . PMID  34307865. 
8. Legates, DR; McCabe, GJ (1999). "Evaluación del uso de medidas de "bondad de ajuste" en la validación de modelos hidrológicos e hidroclimáticos". Water Res. Res . 35 (1): 233–241. Bibcode :1999WRR....35..233L. doi :10.1029/1998WR900018. S2CID  128417849.
9. Ritter, A.; Muñoz-Carpena, R. (2013). "Evaluación del desempeño de modelos hidrológicos: significancia estadística para reducir la subjetividad en evaluaciones de bondad de ajuste". Journal of Hydrology . 480 (1): 33–45. Bibcode :2013JHyd..480...33R. doi :10.1016/j.jhydrol.2012.12.004.
10. Everitt, BS (2002). Diccionario de Estadística de Cambridge (2.ª ed.). CUP. pág. 78. ISBN 978-0-521-81099-9.
11. Casella, Georges (2002). Inferencia estadística (segunda edición). Pacific Grove, California: Duxbury/Thomson Learning. pág. 556. ISBN 9788131503942.
12. Kvalseth, Tarald O. (1985). "Nota de precaución sobre R2". The American Statistician . 39 (4): 279–285. doi :10.2307/2683704. JSTOR  2683704.
13. "Regresión lineal – MATLAB y Simulink". www.mathworks.com .
14. Faraway, Julian James (2005). Modelos lineales con R (PDF) . Chapman & Hall/CRC. ISBN 9781584884255.
15. Raju, Nambury S.; Bilgic, Reyhan; Edwards, Jack E.; Fleer, Paul F. (1997). "Revisión de la metodología: Estimación de la validez poblacional y la validez cruzada, y el uso de pesos iguales en la predicción". Medición psicológica aplicada . 21 (4): 291–305. doi :10.1177/01466216970214001. ISSN  0146-6216. S2CID  122308344.
16. Mordecai Ezekiel (1930), Métodos de análisis de correlación , Wiley , Wikidata  Q120123877, págs. 208–211.
17. Yin, Ping; Fan, Xitao (enero de 2001). "Estimación de la contracción de R 2 en regresión múltiple: una comparación de diferentes métodos analíticos" (PDF) . The Journal of Experimental Education . 69 (2): 203–224. doi :10.1080/00220970109600656. ISSN  0022-0973. S2CID  121614674.
18. Shieh, Gwowen (1 de abril de 2008). "Estimación mejorada de la contracción del coeficiente de correlación múltiple al cuadrado y del coeficiente de validez cruzada al cuadrado". Métodos de investigación organizacional . 11 (2): 387–407. doi :10.1177/1094428106292901. ISSN  1094-4281. S2CID  55098407.
19. Olkin, Ingram; Pratt, John W. (marzo de 1958). "Estimación no sesgada de ciertos coeficientes de correlación". Anales de estadística matemática . 29 (1): 201–211. doi : 10.1214/aoms/1177706717 . ISSN  0003-4851.
20. Karch, Julian (29 de septiembre de 2020). "Mejora del R cuadrado ajustado". Collabra: Psicología . 6 (45). doi : 10.1525/collabra.343 . hdl : 1887/3161248 . ISSN  2474-7394.
21. Richard Anderson-Sprecher, "Comparaciones de modelos y R2", The American Statistician , volumen 48, número 2, 1994, págs. 113-117.
22. Nagelkerke, NJD (septiembre de 1991). "Una nota sobre una definición general del coeficiente de determinación" (PDF) . Biometrika . 78 (3): 691–692. doi :10.1093/biomet/78.3.691. JSTOR  2337038.
23. "regresión - implementación en R del coeficiente de determinación parcial". Validación cruzada .
24. Hoornweg, Victor (2018). "Parte II: Sobre cómo mantener los parámetros fijos". Ciencia: En proceso de envío . Hoornweg Press. ISBN 978-90-829188-0-9.
25. Cox, DD; Snell, EJ (1989). El análisis de datos binarios (2.ª ed.). Chapman y Hall.
26. Magee, L. (1990). " Medidas R ^{2 basadas en pruebas de significación conjunta de razón de verosimilitud y de Wald".} The American Statistician . 44 (3): 250–3. doi :10.1080/00031305.1990.10475731.
27. Nagelkerke, Nico JD (1992). Estimación de relaciones funcionales por máxima verosimilitud, Pays-Bas . Apuntes de clase sobre estadística. Vol. 69. ISBN 978-0-387-97721-8.
28. Página web de OriginLab, http://www.originlab.com/doc/Origin-Help/LR-Algorithm. Consultado el 9 de febrero de 2016.
29. Wright, Sewall (enero de 1921). "Correlación y causalidad". Journal of Agricultural Research . 20 : 557–585.

Lectura adicional

• Gujarati, Damodar N. ; Porter, Dawn C. (2009). Econometría básica (quinta edición). Nueva York: McGraw-Hill/Irwin. págs. 73–78. ISBN 978-0-07-337577-9.
• Hughes, Ann; Grawoig, Dennis (1971). Estadística: una base para el análisis. Lectura: Addison-Wesley. pp. 344–348. ISBN 0-201-03021-7.
• Kmenta, Jan (1986). Elementos de econometría (segunda edición). Nueva York: Macmillan. Págs. 240-243. ISBN. 978-0-02-365070-3.
• Lewis-Beck, Michael S. ; Skalaban, Andrew (1990). "La R -cuadrada: una conversación sincera". Análisis político . 2 : 153–171. doi :10.1093/pan/2.1.153. JSTOR  23317769.
• Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). "El coeficiente de determinación R-cuadrado es más informativo que SMAPE, MAE, MAPE, MSE y RMSE en la evaluación del análisis de regresión". PeerJ Ciencias de la Computación . 7 (e623): e623. doi : 10.7717/peerj-cs.623 . PMC  8279135 . PMID  34307865.