Prueba F

Prueba de hipótesis estadística, en su mayoría utilizando múltiples restricciones

Una prueba f de densidad de probabilidad con d1 y d2 = 10, con un nivel de significancia de 0,05. (La región sombreada en rojo indica la región crítica)

Una prueba F es cualquier prueba estadística utilizada para comparar las varianzas de dos muestras o la razón de varianzas entre múltiples muestras. La estadística de prueba , variable aleatoria F, se utiliza para determinar si los datos probados tienen una distribución F bajo la hipótesis nula verdadera y los supuestos habituales verdaderos sobre el término de error (ε). ^[1] Se utiliza con mayor frecuencia cuando se comparan modelos estadísticos que se han ajustado a un conjunto de datos , con el fin de identificar el modelo que mejor se ajusta a la población de la que se tomaron los datos. Las " pruebas F " exactas surgen principalmente cuando los modelos se han ajustado a los datos utilizando mínimos cuadrados . El nombre fue acuñado por George W. Snedecor , en honor a Ronald Fisher . Fisher desarrolló inicialmente la estadística como la razón de varianza en la década de 1920. ^[2]

Ejemplos comunes

Ejemplos comunes del uso de pruebas F incluyen el estudio de los siguientes casos

• 

  Tabla ANOVA unidireccional con 3 grupos aleatorios, cada uno de los cuales tiene 30 observaciones. El valor F se calcula en la penúltima columna

  Hipótesis de que las medias de un conjunto dado de poblaciones distribuidas normalmente , todas con la misma desviación estándar , son iguales. Esta es quizás la prueba F más conocida y desempeña un papel importante en el análisis de varianza (ANOVA).
  • La prueba F del análisis de varianza (ANOVA) sigue tres supuestos
    1. Normalidad (estadística)
    2. Homogeneidad de varianza
    3. Independencia de errores y muestreo aleatorio

• La hipótesis de que un modelo de regresión propuesto se ajusta bien a los datos . Véase Suma de cuadrados por falta de ajuste .
• La hipótesis de que un conjunto de datos en un análisis de regresión sigue el más simple de dos modelos lineales propuestos que están anidados uno dentro del otro.
• Las pruebas de comparación múltiple se llevan a cabo utilizando los datos necesarios en una prueba F ya completada, si la prueba F conduce al rechazo de la hipótesis nula y el factor en estudio tiene un impacto en la variable dependiente. ^[1]
  • " comparaciones a priori "/"comparaciones planificadas": un conjunto particular de comparaciones
  • "comparaciones por pares": todas las comparaciones posibles
    • es decir, prueba de diferencia menos significativa (LSD) de Fisher, prueba de diferencia honestamente significativa (HSD) de Tukey , prueba de Newman Keuls , prueba de Ducan
  • " comparaciones a posteriori "/ " comparaciones post hoc "/ " comparaciones exploratorias ": elija las comparaciones después de examinar los datos
    • es decir el método de Scheffé

F-prueba de la igualdad de dos varianzas

La prueba F es sensible a la no normalidad . ^{[3] [4]} En el análisis de varianza (ANOVA), las pruebas alternativas incluyen la prueba de Levene , la prueba de Bartlett y la prueba de Brown-Forsythe . Sin embargo, cuando se realiza cualquiera de estas pruebas para probar el supuesto subyacente de homocedasticidad ( es decir, homogeneidad de varianza), como paso preliminar para probar los efectos de la media, hay un aumento en la tasa de error de tipo I experimental . ^[5]

Fórmula y cálculo

La mayoría de las pruebas F surgen al considerar una descomposición de la variabilidad en una colección de datos en términos de sumas de cuadrados . El estadístico de prueba en una prueba F es la relación de dos sumas de cuadrados escaladas que reflejan diferentes fuentes de variabilidad. Estas sumas de cuadrados se construyen de modo que el estadístico tiende a ser mayor cuando la hipótesis nula no es verdadera. Para que el estadístico siga la distribución F bajo la hipótesis nula, las sumas de cuadrados deben ser estadísticamente independientes y cada una debe seguir una distribución χ² escalada . La última condición se garantiza si los valores de los datos son independientes y se distribuyen normalmente con una varianza común .

Análisis de varianza unidireccional

La fórmula para la estadística de prueba F del ANOVA unidireccional es

${\displaystyle F={\frac {\text{explained variance}}{\text{unexplained variance}}},}$

o

${\displaystyle F={\frac {\text{between-group variability}}{\text{within-group variability}}}.}$

La "varianza explicada", o "variabilidad entre grupos", es

${\displaystyle \sum _{i=1}^{K}n_{i}({\bar {Y}}_{i\cdot }-{\bar {Y}})^{2}/(K-1)}$

donde denota la media de la muestra en el i -ésimo grupo, es el número de observaciones en el i -ésimo grupo, denota la media general de los datos y denota el número de grupos. ${\displaystyle {\bar {Y}}_{i\cdot }}$ ${\displaystyle n_{i}}$ ${\displaystyle {\bar {Y}}}$ ${\displaystyle K}$

La "varianza inexplicada", o "variabilidad dentro del grupo", es

${\displaystyle \sum _{i=1}^{K}\sum _{j=1}^{n_{i}}\left(Y_{ij}-{\bar {Y}}_{i\cdot }\right)^{2}/(N-K),}$

donde es la j ^-ésima observación en el i- ^ésimo grupo y es el tamaño total de la muestra. Este estadístico F sigue la distribución F con grados de libertad y bajo la hipótesis nula. El estadístico será grande si la variabilidad entre grupos es grande en relación con la variabilidad dentro del grupo, lo que es poco probable que suceda si las medias poblacionales de todos los grupos tienen el mismo valor. ${\displaystyle Y_{ij}}$ ${\displaystyle K}$ ${\displaystyle N}$ ${\displaystyle d_{1}=K-1}$ ${\displaystyle d_{2}=N-K}$

Tabla F: Valores críticos de nivel 5%, que contienen grados de libertad tanto para el denominador como para el numerador que van del 1 al 20

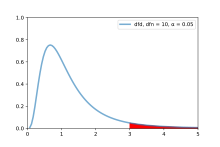
El resultado de la prueba F se puede determinar comparando el valor F calculado y el valor F crítico con un nivel de significancia específico (p. ej., 5%). La tabla F sirve como guía de referencia que contiene valores F críticos para la distribución de la estadística F bajo el supuesto de una hipótesis nula verdadera. Está diseñada para ayudar a determinar el umbral más allá del cual se espera que la estadística F exceda un porcentaje controlado del tiempo (p. ej., 5%) cuando la hipótesis nula es precisa. Para localizar el valor F crítico en la tabla F, se deben utilizar los respectivos grados de libertad. Esto implica identificar la fila y la columna apropiadas en la tabla F que corresponden al nivel de significancia que se está probando (p. ej., 5%). ^[6]

Cómo utilizar los valores críticos F:

Si la estadística F < el valor crítico F

• No se puede rechazar la hipótesis nula
• Rechazar hipótesis alternativa
• No hay diferencias significativas entre los promedios de la muestra
• Las diferencias observadas entre los promedios de las muestras podrían ser causadas razonablemente por el azar en sí.
• El resultado no es estadísticamente significativo

Si la estadística F > el valor crítico F

• Aceptar hipótesis alternativa
• Rechazar la hipótesis nula
• Existen diferencias significativas entre los promedios de la muestra
• Las diferencias observadas entre los promedios de las muestras no podrían razonablemente ser causadas por el azar en sí.
• El resultado es estadísticamente significativo

Tenga en cuenta que cuando solo hay dos grupos para la prueba F de ANOVA de una vía , donde t es la estadística de Student . ${\displaystyle F=t^{2}}$ ${\displaystyle t}$

Ventajas

• Eficiencia de comparación multigrupo: facilita la comparación simultánea de múltiples grupos, mejorando la eficiencia particularmente en situaciones que involucran más de dos grupos.
• Claridad en la comparación de varianzas: ofrecer una interpretación sencilla de las diferencias de varianza entre grupos, contribuyendo a una comprensión clara de los patrones de datos observados.
• Versatilidad entre disciplinas: Demostrar una amplia aplicabilidad en diversos campos, incluidas las ciencias sociales, las ciencias naturales y la ingeniería.

Desventajas

• Sensibilidad a los supuestos: la prueba F es muy sensible a ciertos supuestos, como la homogeneidad de la varianza y la normalidad, que pueden afectar la precisión de los resultados de la prueba.
• Alcance limitado a comparaciones de grupos: la prueba F está diseñada para comparar variaciones entre grupos, lo que la hace menos adecuada para análisis más allá de este alcance específico.
• Desafíos de interpretación: La prueba F no identifica pares de grupos específicos con varianzas distintas. Es necesaria una interpretación cuidadosa y, a menudo, son esenciales pruebas post hoc adicionales para comprender con más detalle las diferencias entre grupos.

Problemas de ANOVA de comparación múltiple

La prueba F en el análisis de varianza unidireccional ( ANOVA ) se utiliza para evaluar si los valores esperados de una variable cuantitativa dentro de varios grupos predefinidos difieren entre sí. Por ejemplo, supongamos que un ensayo médico compara cuatro tratamientos. La prueba F de ANOVA se puede utilizar para evaluar si alguno de los tratamientos es en promedio superior o inferior a los demás frente a la hipótesis nula de que los cuatro tratamientos producen la misma respuesta media. Este es un ejemplo de una prueba "ómnibus", lo que significa que se realiza una sola prueba para detectar cualquiera de varias diferencias posibles. Alternativamente, podríamos realizar pruebas por pares entre los tratamientos (por ejemplo, en el ejemplo del ensayo médico con cuatro tratamientos podríamos realizar seis pruebas entre pares de tratamientos). La ventaja de la prueba F de ANOVA es que no necesitamos especificar previamente qué tratamientos se van a comparar y no necesitamos ajustar para hacer comparaciones múltiples . La desventaja de la prueba F de ANOVA es que si rechazamos la hipótesis nula , no sabemos qué tratamientos se puede decir que son significativamente diferentes de los demás, ni tampoco, si la prueba F se realiza en el nivel α, podemos afirmar que el par de tratamientos con la mayor diferencia de medias es significativamente diferente en el nivel α.

Problemas de regresión

Consideremos dos modelos, 1 y 2, donde el modelo 1 está "anidado" dentro del modelo 2. El modelo 1 es el modelo restringido y el modelo 2 es el modelo sin restricciones. Es decir, el modelo 1 tiene p ₁ parámetros y el modelo 2 tiene p ₂ parámetros, donde p ₁  <  p ₂ , y para cualquier elección de parámetros en el modelo 1, se puede lograr la misma curva de regresión mediante alguna elección de los parámetros del modelo 2.

Un contexto común en este sentido es el de decidir si un modelo se ajusta a los datos significativamente mejor que un modelo ingenuo, en el que el único término explicativo es el término de intersección, de modo que todos los valores predichos para la variable dependiente se establecen como iguales a la media muestral de esa variable. El modelo ingenuo es el modelo restringido, ya que los coeficientes de todas las variables explicativas potenciales se limitan a cero.

Otro contexto común es decidir si hay una ruptura estructural en los datos: en este caso, el modelo restringido utiliza todos los datos en una regresión, mientras que el modelo sin restricciones utiliza regresiones separadas para dos subconjuntos diferentes de los datos. Este uso de la prueba F se conoce como prueba de Chow .

El modelo con más parámetros siempre podrá ajustar los datos al menos tan bien como el modelo con menos parámetros. Por lo tanto, normalmente el modelo 2 dará un mejor ajuste a los datos (es decir, con un menor error) que el modelo 1. Pero a menudo se desea determinar si el modelo 2 da un ajuste significativamente mejor a los datos. Una forma de abordar este problema es utilizar una prueba F.

Si hay n puntos de datos para estimar los parámetros de ambos modelos, entonces se puede calcular la estadística F , dada por

${\displaystyle F={\frac {\left({\frac {{\text{RSS}}_{1}-{\text{RSS}}_{2}}{p_{2}-p_{1}}}\right)}{\left({\frac {{\text{RSS}}_{2}}{n-p_{2}}}\right)}}={\frac {{\text{RSS}}_{1}-{\text{RSS}}_{2}}{{\text{RSS}}_{2}}}\cdot {\frac {n-p_{2}}{p_{2}-p_{1}}},}$

donde RSS _i es la suma de los cuadrados de los residuos del modelo i . Si el modelo de regresión se ha calculado con ponderaciones, entonces reemplace RSS _i con χ ² , la suma ponderada de los cuadrados de los residuos. Bajo la hipótesis nula de que el modelo 2 no proporciona un ajuste significativamente mejor que el modelo 1, F tendrá una distribución F , con ( p ₂ − p ₁ ,  n − p ₂ ) grados de libertad . La hipótesis nula se rechaza si la F calculada a partir de los datos es mayor que el valor crítico de la distribución F para alguna probabilidad de falso rechazo deseada (por ejemplo, 0,05). Dado que F es una función monótona de la estadística de razón de verosimilitud, la prueba F es una prueba de razón de verosimilitud .

Véase también

• Bondad de ajuste

Referencias

1. Berger, Paul D.; Maurer, Robert E.; Celli, Giovana B. (2018). Diseño experimental. Cham: Springer International Publishing. pág. 108. doi :10.1007/978-3-319-64583-4. ISBN 978-3-319-64582-7.
2. Lomax, Richard G. (2007). Conceptos estadísticos: un segundo curso . p. 10. ISBN 978-0-8058-5850-1.
3. Box, GEP (1953). "No normalidad y pruebas de varianzas". Biometrika . 40 (3/4): 318–335. doi :10.1093/biomet/40.3-4.318. JSTOR  2333350.
4. Markowski, Carol A; Markowski, Edward P. (1990). "Condiciones para la efectividad de una prueba preliminar de varianza". The American Statistician . 44 (4): 322–326. doi :10.2307/2684360. JSTOR  2684360.
5. Sawilowsky, S. (2002). «Fermat, Schubert, Einstein y Behrens–Fisher: la diferencia probable entre dos medias cuando σ12 ≠ σ22». Journal of Modern Applied Statistical Methods . 1 (2): 461–472. doi : 10.22237/jmasm/1036109940 . Archivado desde el original el 2015-04-03 . Consultado el 2015-03-30 .
6. Siegel, Andrew F. (1 de enero de 2016), Siegel, Andrew F. (ed.), "Capítulo 15 - ANOVA: Pruebas de diferencias entre muchas muestras y mucho más", Practical Business Statistics (séptima edición) , Academic Press, págs. 469–492, doi :10.1016/b978-0-12-804250-2.00015-8, ISBN 978-0-12-804250-2, consultado el 10 de diciembre de 2023

Lectura adicional

• Fox, Karl A. (1980). Estadísticas económicas intermedias (segunda edición). Nueva York: John Wiley & Sons. pp. 290–310. ISBN 0-88275-521-8.
• Johnston, John (1972). Métodos econométricos (segunda edición). Nueva York: McGraw-Hill. págs. 35–38.
• Kmenta, Jan (1986). Elementos de econometría (segunda edición). Nueva York: Macmillan. Págs. 147-148. ISBN. 0-02-365070-2.
• Maddala, GS ; Lahiri, Kajal (2009). Introducción a la econometría (Cuarta ed.). Chichester: Wiley. págs. 155-160. ISBN 978-0-470-01512-4.

Enlaces externos

• Tabla de valores críticos de la prueba F
• Calculadora gratuita para pruebas F
• La prueba F para la regresión lineal
• Conferencia sobre econometría (tema: pruebas de hipótesis) en YouTube por Mark Thoma