Curva de Lorenz

Representación gráfica de la distribución del ingreso o de la riqueza

Una curva de Lorenz típica

En economía , la curva de Lorenz es una representación gráfica de la distribución del ingreso o de la riqueza . Fue desarrollada por Max O. Lorenz en 1905 para representar la desigualdad en la distribución de la riqueza .

La curva es un gráfico que muestra la proporción de ingresos o riqueza total asumida por el x % inferior de la población, aunque esto no es rigurosamente cierto para una población finita (ver más abajo). A menudo se utiliza para representar la distribución del ingreso , donde muestra para el x % inferior de hogares, qué porcentaje ( y %) del ingreso total tienen. El porcentaje de hogares se traza en el eje x , el porcentaje de ingresos en el eje y . También se puede utilizar para mostrar la distribución de activos . En tal uso, muchos economistas lo consideran una medida de desigualdad social .

El concepto es útil para describir la desigualdad entre el tamaño de los individuos en ecología ^[1] y en estudios de biodiversidad , donde la proporción acumulada de especies se grafica contra la proporción acumulada de individuos. ^[2] También es útil en el modelado empresarial : por ejemplo, en finanzas de consumo , para medir el porcentaje real y % de morosidades atribuibles al x % de personas con peores puntuaciones de riesgo . Las curvas de Lorenz también se aplicaron a la epidemiología y la salud pública , por ejemplo, para medir la desigualdad pandémica como la distribución de la incidencia acumulada nacional (y%) generada por la población residente en áreas (x%) clasificadas con respecto a su tasa de ataque epidémico local . ^[3]

Explicación

Derivación de la curva de Lorenz y del coeficiente de Gini para el ingreso mundial en 2011

Datos del año 2005.

Los puntos de la curva de Lorenz representan afirmaciones como: "el 20% inferior de todos los hogares tiene el 10% del ingreso total".

Una distribución de ingresos perfectamente igualitaria sería aquella en la que todas las personas tuvieran los mismos ingresos. En este caso, el N % más pobre de la sociedad siempre tendría el N % de los ingresos. Esto se puede representar mediante la línea recta y = x ; llamada la "línea de igualdad perfecta".

En cambio, una distribución perfectamente desigual sería aquella en la que una persona tiene todos los ingresos y el resto no tiene ninguno. En ese caso, la curva estaría en y = 0% para todos los x < 100%, e y = 100% cuando x = 100%. Esta curva se denomina "línea de desigualdad perfecta".

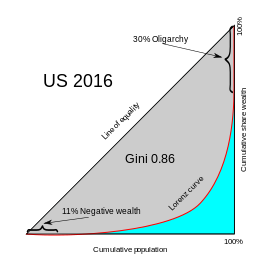
El coeficiente de Gini es la relación entre el área entre la línea de igualdad perfecta y la curva de Lorenz observada y el área entre la línea de igualdad perfecta y la línea de desigualdad perfecta. Cuanto mayor sea el coeficiente, más desigual será la distribución. En el diagrama de la derecha, esto se expresa mediante la relación A /( A + B ), donde A y B son las áreas de las regiones marcadas en el diagrama.

Definición y cálculo

Curva de Lorenz para la distribución de la riqueza en Estados Unidos en 2016 que muestra riqueza negativa y oligarquía

La curva de Lorenz es un gráfico de probabilidad (un gráfico P–P ) que compara la distribución de una variable con una distribución uniforme hipotética de esa variable. Por lo general, se puede representar mediante una función L ( F ), donde F , la porción acumulada de la población, está representada por el eje horizontal, y L , la porción acumulada de la riqueza o los ingresos totales, está representada por el eje vertical.

La curva L no necesita ser una función de F que aumenta suavemente . Para las distribuciones de riqueza puede haber oligarquías o personas con riqueza negativa, por ejemplo. ^[4]

Para una distribución discreta de Y dada por los valores y ₁ , ..., y _n en orden no decreciente ( y _i ≤ y _{i +1} ) y sus probabilidades, la curva de Lorenz es la función lineal continua por partes que conecta los puntos ( F _i , L _i ), i = 0 a n , donde F ₀ = 0, L ₀ = 0, y para i = 1 a n : ${\displaystyle f(y_{j}):=\Pr(Y=y_{j})}$ $${\displaystyle {\begin{aligned}F_{i}&:=\sum _{j=1}^{i}f(y_{j})\\S_{i}&:=\sum _{j=1}^{i}f(y_{j})\,y_{j}\\L_{i}&:={\frac {S_{i}}{S_{n}}}\end{aligned}}}$$

Cuando todos los y _i son igualmente probables con probabilidades 1/ n esto se simplifica a $${\displaystyle {\begin{aligned}F_{i}&={\frac {i}{n}}\\S_{i}&={\frac {1}{n}}\sum _{j=1}^{i}\;y_{j}\\L_{i}&={\frac {S_{i}}{S_{n}}}\end{aligned}}}$$

Para una distribución continua con la función de densidad de probabilidad f y la función de distribución acumulativa F , la curva de Lorenz L viene dada por: donde denota el promedio. La curva de Lorenz L ( F ) puede entonces trazarse como una función paramétrica en x : L ( x ) vs. F ( x ). En otros contextos, la cantidad calculada aquí se conoce como distribución sesgada por la longitud (o por el tamaño); también tiene un papel importante en la teoría de renovación. $${\displaystyle L(F(x))={\frac {\int _{-\infty }^{x}t\,f(t)\,dt}{\int _{-\infty }^{\infty }t\,f(t)\,dt}}={\frac {\int _{-\infty }^{x}t\,f(t)\,dt}{\mu }}}$$ ${\displaystyle \mu }$

Alternativamente, para una función de distribución acumulativa F ( x ) con x ( F ) inversa, la curva de Lorenz L ( F ) está dada directamente por: $${\displaystyle L(F)={\frac {\int _{0}^{F}x(F_{1})\,dF_{1}}{\int _{0}^{1}x(F_{1})\,dF_{1}}}}$$

La inversa x ( F ) puede no existir porque la función de distribución acumulativa tiene intervalos de valores constantes. Sin embargo, la fórmula anterior todavía puede aplicarse generalizando la definición de x ( F ): donde inf es el ínfimo . $${\displaystyle x(F_{1})=\inf\{y:F(y)\geq F_{1}\}}$$

Para ver un ejemplo de una curva de Lorenz, consulte distribución de Pareto .

Propiedades

Un ejemplo práctico de una curva de Lorenz: las curvas de Lorenz de Dinamarca, Hungría y Namibia

Una curva de Lorenz siempre comienza en (0,0) y termina en (1,1).

La curva de Lorenz no está definida si la media de la distribución de probabilidad es cero o infinita.

La curva de Lorenz de una distribución de probabilidad es una función continua . Sin embargo, las curvas de Lorenz que representan funciones discontinuas pueden construirse como el límite de las curvas de Lorenz de distribuciones de probabilidad, siendo un ejemplo la línea de desigualdad perfecta.

La información de una curva de Lorenz se puede resumir mediante el coeficiente de Gini y el coeficiente de asimetría de Lorenz . ^[1]

La curva de Lorenz no puede elevarse por encima de la línea de perfecta igualdad.

Una curva de Lorenz que nunca cae por debajo de una segunda curva de Lorenz y al menos una vez pasa por encima de ella, tiene dominio de Lorenz sobre la segunda. ^[5]

Si la variable que se mide no puede tomar valores negativos, la curva de Lorenz:

• no puede hundirse por debajo de la línea de la desigualdad perfecta,
• está aumentando .

Sin embargo, tenga en cuenta que una curva de Lorenz para el patrimonio neto comenzaría siendo negativa debido al hecho de que algunas personas tienen un patrimonio neto negativo debido a las deudas.

La curva de Lorenz es invariante bajo escala positiva. Si X es una variable aleatoria, para cualquier número positivo c la variable aleatoria c X tiene la misma curva de Lorenz que X .

La curva de Lorenz se invierte dos veces, una alrededor de F = 0,5 y otra alrededor de L = 0,5, por negación. Si X es una variable aleatoria con curva de Lorenz L _X ( F ), entonces − X tiene la curva de Lorenz:

L _{− X} = 1 − L _X (1 −  F )

La curva de Lorenz se modifica mediante traslaciones de modo que la brecha de igualdad F  −  L ( F ) cambia en proporción a la relación entre las medias original y trasladada. Si X es una variable aleatoria con una curva de Lorenz L _X ( F ) y una media μ _X , entonces para cualquier constante c ≠ − μ _X , X + c tiene una curva de Lorenz definida por: $${\displaystyle F-L_{X+c}(F)={\frac {\mu _{X}}{\mu _{X}+c}}(F-L_{X}(F))}$$

Para una función de distribución acumulativa F ( x ) con media μ e inversa (generalizada) x ( F ), entonces para cualquier F con 0 < F < 1 :

• Si la curva de Lorenz es diferenciable: $${\displaystyle {\frac {dL(F)}{dF}}={\frac {x(F)}{\mu }}}$$
• Si la curva de Lorenz es dos veces diferenciable, entonces la función de densidad de probabilidad f ( x ) existe en ese punto y: $${\displaystyle {\frac {d^{2}L(F)}{dF^{2}}}={\frac {1}{\mu \,f(x(F))}}\,}$$
• Si L ( F ) es continuamente diferenciable, entonces la tangente de L ( F ) es paralela a la línea de igualdad perfecta en el punto F ( μ ). Este es también el punto en el que la brecha de igualdad F  −  L ( F ), la distancia vertical entre la curva de Lorenz y la línea de igualdad perfecta, es máxima. El tamaño de la brecha es igual a la mitad de la desviación absoluta media relativa : $${\displaystyle F(\mu )-L(F(\mu ))={\frac {\text{mean absolute deviation}}{2\,\mu }}}$$

Véase también

• Distribución (economía)
• Distribución de la riqueza
• Economía del bienestar
• Indicadores de desigualdad de ingresos
• Coeficiente de Gini
• Índice Hoover (también conocido como índice Robin Hood)
• Análisis ROC
• Bienestar social (ciencia política)
• Desigualdad económica
• Ley de Zipf
• Distribución de Pareto
• Desviación media
• La curva del elefante

Referencias

1. Damgaard, Christian; Jacob Weiner (2000). "Descripción de la desigualdad en el tamaño o la fecundidad de las plantas". Ecología . 81 (4): 1139–1142. doi :10.1890/0012-9658(2000)081[1139:DIIPSO]2.0.CO;2.
2. Wittebolle, Lieven; et al. (2009). "La uniformidad inicial de la comunidad favorece la funcionalidad bajo estrés selectivo". Nature . 458 (7238): 623–626. Bibcode :2009Natur.458..623W. doi :10.1038/nature07840. PMID  19270679. S2CID  4419280.
3. Nguyen, Quang D.; Chang, Sheryl L.; Jamerlan, Christina M.; Prokopenko, Mikhail (2023). "Medición de la distribución desigual de la gravedad de la pandemia en los distintos años censales, variantes de interés e intervenciones". Métricas de salud de la población . 21 (17): 17. doi : 10.1186/s12963-023-00318-6 . PMC 10613397 . PMID  37899455. 
4. Li, Jie; Boghosian, Bruce M.; Li, Chengli (14 de febrero de 2018). "El modelo de riqueza afín: un modelo de intercambio de activos basado en agentes que permite agentes de riqueza negativa y su validación empírica". arXiv : 1604.02370v2 . {{cite journal}}: Requiere citar revista |journal=( ayuda )
5. Bishop, John A.; Formby, John P.; Smith, W. James (1991). "Dominancia de Lorenz y bienestar: cambios en la distribución del ingreso en Estados Unidos, 1967-1986". The Review of Economics and Statistics . 73 (1): 134–139. doi :10.2307/2109695. ISSN  0034-6535. JSTOR  2109695.

Lectura adicional

• Lorenz, MO (1905). "Métodos de medición de la concentración de la riqueza". Publicaciones de la Asociación Estadounidense de Estadística . 9 (70). Publicaciones de la Asociación Estadounidense de Estadística, vol. 9, núm. 70: 209–219. Bibcode :1905PAmSA...9..209L. doi :10.2307/2276207. JSTOR  2276207. S2CID  154048722.
• Gastwirth, Joseph L. (1972). "La estimación de la curva de Lorenz y el índice de Gini". Revista de Economía y Estadística . 54 (3). Revista de Economía y Estadística, vol. 54, núm. 3: 306–316. doi :10.2307/1937992. JSTOR  1937992.
• Chakravarty, SR (1990). Índices éticos y sociales . Nueva York: Springer-Verlag. ISBN 0-387-52274-3.
• Anand, Sudhir (1983). Desigualdad y pobreza en Malasia . Nueva York: Oxford University Press. ISBN 0-19-520153-1.

Enlaces externos

• WIID Archivado el 13 de marzo de 2011 en Wayback Machine : Base de datos sobre desigualdad de ingresos en el mundo, una fuente de información sobre desigualdad, recopilada por WIDER (Instituto Mundial de Investigación en Economía del Desarrollo, parte de la Universidad de las Naciones Unidas)
• glcurve: módulo de Stata para trazar la curva de Lorenz (escriba "findit glcurve" o "ssc install glcurve" en el mensaje de Stata para instalarlo)
• Complemento gratuito de STATA para calcular medidas de desigualdad y pobreza
• El software gratuito en línea (calculadora) calcula el coeficiente de Gini, traza la curva de Lorenz y calcula muchas otras medidas de concentración para cualquier conjunto de datos.
• Calculadora gratuita: scripts en línea y descargables ( Python y Lua ) para las desigualdades de Atkinson, Gini y Hoover
• Los usuarios del software de análisis de datos R pueden instalar el paquete "ineq" que permite calcular una variedad de índices de desigualdad, incluidos Gini, Atkinson y Theil.
• Un paquete de desigualdades de MATLAB archivado el 4 de octubre de 2008 en Wayback Machine , que incluye código para calcular los índices de Gini, Atkinson y Theil y para trazar la curva de Lorenz. Hay muchos ejemplos disponibles.
• Un folleto completo sobre la curva de Lorenz que incluye varias aplicaciones, incluida una hoja de cálculo de Excel que grafica las curvas de Lorenz y calcula los coeficientes de Gini, así como los coeficientes de variación.
• LORENZ 3.0 es un cuaderno de Mathematica que dibuja muestras de curvas de Lorenz y calcula coeficientes de Gini y coeficientes de asimetría de Lorenz a partir de datos en una hoja de Excel.