Cuadrupolo

Disposición que crea un campo cuadrupolo de algún tipo

Un cuadrupolo o cuadripolo es uno de una secuencia de configuraciones de cosas como carga eléctrica o corriente , o masa gravitacional que pueden existir en forma ideal, pero generalmente es solo parte de una expansión multipolar de una estructura más compleja que refleja varios órdenes de complejidad.

Definición matemática

El tensor de momento cuadrupolar Q es un tensor de rango dos : matriz 3×3. Existen varias definiciones, pero normalmente se expresa en forma sin traza (es decir, ). El tensor de momento cuadrupolar tiene, por lo tanto, nueve componentes, pero debido a la simetría de transposición y la propiedad de traza cero , en esta forma solo cinco de ellos son independientes. ${\displaystyle Q_{xx}+Q_{yy}+Q_{zz}=0}$

Para un sistema discreto de cargas o masas puntuales en el caso de un cuadrupolo gravitacional, cada una con carga o masa y posición relativa al origen del sistema de coordenadas, los componentes de la matriz Q se definen por: ${\displaystyle \ell }$ ${\displaystyle q_{\ell }}$ ${\displaystyle m_{\ell }}$ ${\displaystyle \mathbf {r} _{\ell }=\left(r_{x\ell },r_{y\ell },r_{z\ell }\right)}$

${\displaystyle Q_{ij}=\sum _{\ell }q_{\ell }\left(3r_{i\ell }r_{j\ell }-\left\|\mathbf {r} _{\ell }\right\|^{2}\delta _{ij}\right).}$

Los índices recorren las coordenadas cartesianas y son el delta de Kronecker . Esto significa que deben ser iguales, hasta el signo, a las distancias desde el punto a hiperplanos mutuamente perpendiculares para que el delta de Kronecker sea igual a 1. ${\displaystyle i,j}$ ${\displaystyle x,y,z}$ ${\displaystyle \delta _{ij}}$ ${\displaystyle x,y,z}$ ${\displaystyle n}$

En la forma sin traza, el momento cuadrupolar a veces se expresa como:

${\displaystyle Q_{ij}=\sum _{\ell }q_{\ell }r_{i\ell }r_{j\ell }}$

Esta forma se utiliza en la literatura sobre el método multipolar rápido . La conversión entre estas dos formas se puede lograr fácilmente utilizando un operador de desvío. ^[1]

Para un sistema continuo con densidad de carga, o densidad de masa, , los componentes de Q se definen mediante la integral sobre el espacio cartesiano r : ^[2] ${\displaystyle \rho (x,y,z)}$

${\displaystyle Q_{ij}=\int \,\rho (\mathbf {r} )\left(3r_{i}r_{j}-\left\|\mathbf {r} \right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r} }$

Al igual que con cualquier momento multipolar, si un momento de orden inferior, monopolar o dipolar en este caso, es distinto de cero, entonces el valor del momento cuadrupolar depende de la elección del origen de coordenadas . Por ejemplo, un dipolo de dos cargas puntuales de signo opuesto y misma fuerza, que no tiene momento monopolar, puede tener un momento cuadrupolar distinto de cero si el origen se desplaza lejos del centro de la configuración exactamente entre las dos cargas; o el momento cuadrupolar se puede reducir a cero con el origen en el centro. Por el contrario, si los momentos monopolar y dipolar se anulan, pero el momento cuadrupolar no, por ejemplo, cuatro cargas de la misma fuerza, dispuestas en un cuadrado, con signos alternos, entonces el momento cuadrupolar es independiente de las coordenadas.

Si cada carga es la fuente de un campo "potencial", como el campo eléctrico o gravitacional , la contribución al potencial del campo del momento cuadrupolar es: ${\displaystyle 1/r}$

${\displaystyle V_{\text{q}}(\mathbf {R} )={\frac {k}{|\mathbf {R} |^{3}}}\sum _{i,j}{\frac {1}{2}}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ ,}$

donde R es un vector con origen en el sistema de cargas y R̂ es el vector unitario en la dirección de R . Es decir, para son las componentes cartesianas del vector unitario que apuntan desde el origen al punto del campo. Aquí, es una constante que depende del tipo de campo y de las unidades que se utilicen. ${\displaystyle {\hat {R}}_{i}}$ ${\displaystyle i=x,y,z}$ ${\displaystyle k}$

Cuadrupolo eléctrico

Diagrama de contorno de las superficies equipotenciales de un campo cuadrupolo eléctrico

Un ejemplo sencillo de cuadrupolo eléctrico consiste en cargas positivas y negativas alternadas, dispuestas en las esquinas de un cuadrado. El momento monopolar (sólo la carga total) de esta disposición es cero. De manera similar, el momento dipolar es cero, independientemente del origen de coordenadas que se haya elegido. Pero el momento cuadrupolo de la disposición del diagrama no se puede reducir a cero, independientemente de dónde coloquemos el origen de coordenadas. El potencial eléctrico de un cuadrupolo de carga eléctrica está dado por ^[3]

${\displaystyle V_{\text{q}}(\mathbf {R} )={\frac {1}{4\pi \varepsilon _{0}}}{\frac {1}{|\mathbf {R} |^{3}}}\sum _{i,j}{\frac {1}{2}}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ ,}$

donde es la permitividad eléctrica , y sigue la definición anterior. ${\displaystyle \varepsilon _{0}}$ ${\displaystyle Q_{ij}}$

Alternativamente, otras fuentes ^[4] incluyen el factor de la mitad en el propio tensor, de modo que: ${\displaystyle Q_{ij}}$

${\displaystyle Q_{ij}=\int \,\rho (\mathbf {r} )\left({\frac {3}{2}}r_{i}r_{j}-{\frac {1}{2}}\left\|\mathbf {r} \right\|^{2}\delta _{ij}\right)\,d^{3}\mathbf {r} }$, y

${\displaystyle V_{\text{q}}(\mathbf {R} )={\frac {1}{4\pi \varepsilon _{0}}}{\frac {1}{|\mathbf {R} |^{3}}}\sum _{i,j}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ ,}$

lo que hace más explícita la conexión con los polinomios de Legendre que resultan de la expansión multipolar, es decir aquí ${\textstyle P_{2}(x)={\frac {3}{2}}x^{2}-{\frac {1}{2}}.}$

Generalización: multipolos superiores

Una generalización extrema (" octopolo puntual ") sería: Ocho cargas puntuales alternas en los ocho vértices de un paralelepípedo , p. ej., de un cubo con longitud de arista a . El "momento octopolar" de esta disposición correspondería, en el "límite octopolar" a un tensor diagonal distinto de cero de orden tres. Se obtendrían multipolos aún superiores, p. ej. de orden , mediante disposiciones dipolares (cuadrupolares, octopolares, ...) de dipolos puntuales (cuadrupolos, octopolos, ...), no monopolos puntuales, de orden inferior, p. ej., . ${\textstyle \lim _{a\to 0}{a^{3}\cdot Q}\to {\text{const. }}}$ ${\displaystyle 2^{\ell }}$ ${\displaystyle 2^{\ell -1}}$

Cuadrupolo magnético

Bobinas que producen un campo cuadrupolo

Esquema de un imán cuadrupolo (" cuatro polos ")

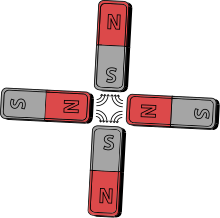
Todas las fuentes magnéticas conocidas dan campos dipolares. Sin embargo, es posible hacer un cuadrupolo magnético colocando cuatro imanes de barra idénticos perpendiculares entre sí de manera que el polo norte de uno esté junto al sur del otro. Esta configuración anula el momento dipolar y da lugar a un momento cuadrupolo, y su campo disminuirá a grandes distancias más rápido que el de un dipolo.

A la derecha se muestra un ejemplo de un cuadrupolo magnético, que involucra imanes permanentes. Los electroimanes de diseño conceptual similar (llamados imanes cuadrupolos ) se utilizan comúnmente para enfocar haces de partículas cargadas en aceleradores de partículas y líneas de transporte de haces, un método conocido como enfoque fuerte . Hay cuatro puntas de polo de acero, dos polos norte magnéticos opuestos y dos polos sur magnéticos opuestos. El acero se magnetiza mediante una gran corriente eléctrica que fluye en las bobinas de tubería enrolladas alrededor de los polos.

Un momento cuadrupolo magnético cambiante produce radiación electromagnética .

Cuadrupolo gravitacional

El cuadrupolo de masa es análogo al cuadrupolo de carga eléctrica, donde la densidad de carga simplemente se reemplaza por la densidad de masa y se agrega un signo negativo porque las masas siempre son positivas y la fuerza es atractiva. El potencial gravitacional se expresa entonces como:

${\displaystyle V_{\text{q}}(\mathbf {R} )=-{\frac {G}{2|\mathbf {R} |^{3}}}\sum _{i,j}Q_{ij}\,{\hat {R}}_{i}{\hat {R}}_{j}\ .}$

Por ejemplo, debido a que la Tierra está rotando, es achatada (aplanada en los polos). Esto le da un momento cuadripolar distinto de cero. Si bien la contribución de este cuadripolo al campo gravitatorio de la Tierra es extremadamente importante para los satélites artificiales cercanos a la Tierra, es menos importante para la Luna porque el término disminuye rápidamente. ${\displaystyle {1}/{|\mathbf {R} |^{3}}}$

El momento cuadrupolar de masa también es importante en la relatividad general porque, si cambia en el tiempo, puede producir radiación gravitatoria , similar a la radiación electromagnética producida por dipolos eléctricos o magnéticos oscilantes y multipolos superiores. Sin embargo, solo el cuadrupolar y los momentos superiores pueden radiar gravitatoriamente. El monopolo de masa representa la masa-energía total en un sistema, que se conserva, por lo que no emite radiación. De manera similar, el dipolo de masa corresponde al centro de masa de un sistema y su primera derivada representa el momento, que también es una cantidad conservada, por lo que el dipolo de masa tampoco emite radiación. El cuadrupolar de masa, sin embargo, puede cambiar en el tiempo y es la contribución de orden más bajo a la radiación gravitatoria. ^[5]

El ejemplo más simple e importante de un sistema radiante es un par de puntos de masa con masas iguales que orbitan entre sí en una órbita circular, una aproximación a, por ejemplo, el caso especial de los agujeros negros binarios . Dado que el momento dipolar es constante, podemos colocar por conveniencia el origen de coordenadas justo entre los dos puntos. Entonces, el momento dipolar será cero, y si también escalamos las coordenadas de modo que los puntos estén a una distancia unitaria del centro, en dirección opuesta, el momento cuadrupolar del sistema será simplemente

${\displaystyle Q_{ij}=M\left(3x_{i}x_{j}-|\mathbf {x} |^{2}\delta _{ij}\right)}$

donde M es la masa de cada punto, y son componentes del vector de posición (unitario) de uno de los puntos. A medida que orbitan, este vector x rotará, lo que significa que tendrá una primera derivada temporal distinta de cero y también una segunda derivada temporal distinta de cero (esto es, por supuesto, cierto independientemente de la elección del sistema de coordenadas). Por lo tanto, el sistema irradiará ondas gravitacionales. La energía perdida de esta manera se observó por primera vez en el período cambiante del binario Hulse-Taylor , un púlsar en órbita con otra estrella de neutrones de masa similar. ${\displaystyle x_{i}}$

De la misma manera que los multipolos de carga eléctrica y corriente contribuyen al campo electromagnético, los multipolos de masa y de corriente-masa contribuyen al campo gravitacional en la relatividad general, lo que provoca los llamados efectos gravitomagnéticos . Los multipolos de masa-corriente cambiantes también pueden emitir radiación gravitacional. Sin embargo, las contribuciones de los multipolos de corriente normalmente serán mucho menores que las del cuadrupolo de masa.

Véase también

• Expansión multipolar
• Momentos multipolares
• Armónicos sólidos
• Momentos multipolares axiales
• Momentos multipolares cilíndricos
• Momentos multipolares esféricos
• Expansión de Laplace
• Polinomios de Legendre
• Trampa de iones cuadrupolo
• Analizador de masas cuadrupolo
• Interacción de intercambio multipolar
• Cable cuádruple en estrella
• Lente magnética
• Fórmula del cuadrupolo

Referencias

1. Applequist, J. (1989). "Formas tensoriales cartesianas sin trazas para funciones armónicas esféricas: nuevos teoremas y aplicaciones a la electrostática de medios dieléctricos". Journal of Physics A: Mathematical and General . 22 (20): 4303–4330. Bibcode :1989JPhA...22.4303A. doi :10.1088/0305-4470/22/20/011.
2. Weisstein, Eric. "Momento cuadrupolo eléctrico". Eric Weisstein's World of Physics . Wolfram Research . Consultado el 8 de mayo de 2012 .
3. Jackson, John David (1975). Electrodinámica clásica . John Wiley & Sons . ISBN 0-471-43132-X.
4. Griffiths, David J. (2013). Introducción a la electrodinámica, 4.ª ed . Pearson. págs. 153, 165.
5. Thorne, Kip S. (abril de 1980). "Expansiones multipolares de la radiación gravitacional" (PDF) . Reseñas de física moderna . 52 (2): 299–339. Bibcode :1980RvMP...52..299T. doi :10.1103/RevModPhys.52.299.

Enlaces externos

• Expansión multipolar