
Birrefringencia significa doble refracción. Es la propiedad óptica de un material que tiene un índice de refracción que depende de la polarización y la dirección de propagación de la luz . [1] Estos materiales ópticamente anisotrópicos se describen como birrefringentes o birrefractivos . La birrefringencia a menudo se cuantifica como la diferencia máxima entre los índices de refracción exhibidos por el material. Los cristales con estructuras cristalinas no cúbicas a menudo son birrefringentes, al igual que los plásticos bajo tensión mecánica .
La birrefringencia es responsable del fenómeno de la doble refracción , por el cual un rayo de luz, al incidir sobre un material birrefringente, se divide por polarización en dos rayos que toman caminos ligeramente diferentes. Este efecto fue descrito por primera vez por el científico danés Rasmus Bartholin en 1669, quien lo observó [2] en cristales de espato de Islandia ( calcita ) que tienen una de las birrefringencias más fuertes. En el siglo XIX Augustin-Jean Fresnel describió el fenómeno en términos de polarización, entendiendo la luz como una onda con componentes de campo en polarización transversal (perpendicular a la dirección del vector de onda). [3] [4]

A continuación se presenta una descripción matemática de la propagación de ondas en un medio birrefringente. A continuación se presenta una explicación cualitativa del fenómeno.
El tipo más simple de birrefringencia se describe como uniaxial , lo que significa que hay una sola dirección que gobierna la anisotropía óptica por lo que todas las direcciones perpendiculares a ella (o en un ángulo dado con ella) son ópticamente equivalentes. Por lo tanto, girar el material alrededor de este eje no cambia su comportamiento óptico. Esta dirección especial se conoce como el eje óptico del material. La luz que se propaga paralela al eje óptico (cuya polarización es siempre perpendicular al eje óptico) está gobernada por un índice de refracción n o (por "ordinario") independientemente de su polarización específica. Para los rayos con cualquier otra dirección de propagación, hay una polarización lineal que es perpendicular al eje óptico, y un rayo con esa polarización se llama rayo ordinario y está gobernado por el mismo valor de índice de refracción n o . Para un rayo que se propaga en la misma dirección pero con una polarización perpendicular a la del rayo ordinario, la dirección de polarización será en parte en la dirección del eje óptico (paralela a él), y este rayo extraordinario estará regido por un índice de refracción diferente, dependiente de la dirección . Debido a que el índice de refracción depende de la polarización cuando la luz no polarizada entra en un material birrefringente uniaxial, se divide en dos haces que viajan en direcciones diferentes, uno con la polarización del rayo ordinario y el otro con la polarización del rayo extraordinario. El rayo ordinario siempre experimentará un índice de refracción de n o , mientras que el índice de refracción del rayo extraordinario estará entre n o y n e , dependiendo de la dirección del rayo, como se describe por el elipsoide de índice . La magnitud de la diferencia se cuantifica mediante la birrefringencia [5]
La propagación (así como el coeficiente de reflexión ) del rayo ordinario se describe simplemente por n o como si no hubiera birrefringencia involucrada. El rayo extraordinario, como su nombre lo sugiere, se propaga a diferencia de cualquier onda en un material óptico isotrópico. Su refracción (y reflexión) en una superficie se puede entender utilizando el índice de refracción efectivo (un valor entre n o y n e ). Su flujo de potencia (dado por el vector de Poynting ) no está exactamente en la dirección del vector de onda . Esto causa un desplazamiento adicional en ese rayo, incluso cuando se lanza con una incidencia normal, como se observa popularmente utilizando un cristal de calcita como el fotografiado arriba. Al girar el cristal de calcita, una de las dos imágenes, la del rayo extraordinario, girará ligeramente alrededor de la del rayo ordinario, que permanece fija. [ verificación necesaria ]
Cuando la luz se propaga a lo largo o de forma ortogonal al eje óptico, no se produce dicho desplazamiento lateral. En el primer caso, ambas polarizaciones son perpendiculares al eje óptico y tienen el mismo índice de refracción efectivo, por lo que no hay rayo extraordinario. En el segundo caso, el rayo extraordinario se propaga a una velocidad de fase diferente (que corresponde a n e ) pero aún tiene el flujo de potencia en la dirección del vector de onda . Un cristal con su eje óptico en esta orientación, paralelo a la superficie óptica, puede utilizarse para crear una placa de onda , en la que no hay distorsión de la imagen sino una modificación intencional del estado de polarización de la onda incidente. Por ejemplo, una placa de cuarto de onda se utiliza comúnmente para crear polarización circular a partir de una fuente polarizada linealmente.
El caso de los llamados cristales biaxiales es sustancialmente más complejo. [6] Estos se caracterizan por tres índices de refracción correspondientes a tres ejes principales del cristal. Para la mayoría de las direcciones de los rayos, ambas polarizaciones se clasificarían como rayos extraordinarios pero con diferentes índices de refracción efectivos. Al tratarse de ondas extraordinarias, la dirección del flujo de potencia no es idéntica a la dirección del vector de onda en ninguno de los dos casos.
Los dos índices de refracción se pueden determinar utilizando los elipsoides de índice para direcciones dadas de la polarización. Nótese que para los cristales biaxiales el elipsoide de índice no será un elipsoide de revolución (" esferoide ") sino que se describe mediante tres índices de refracción principales desiguales n α , n β y n γ . Por lo tanto, no hay un eje alrededor del cual una rotación deje invariables las propiedades ópticas (como ocurre con los cristales uniaxiales cuyo elipsoide de índice es un esferoide).
Aunque no existe un eje de simetría, existen dos ejes ópticos o binormales que se definen como direcciones a lo largo de las cuales la luz puede propagarse sin birrefringencia, es decir, direcciones a lo largo de las cuales la longitud de onda es independiente de la polarización. [6] Por esta razón, los materiales birrefringentes con tres índices de refracción distintos se denominan biaxiales . Además, existen dos ejes distintos conocidos como ejes de rayos ópticos o biradiales a lo largo de los cuales la velocidad de grupo de la luz es independiente de la polarización.
Cuando un haz de luz arbitrario incide sobre la superficie de un material birrefringente con una incidencia no normal, el componente de polarización normal al eje óptico (rayo ordinario) y el otro componente de polarización lineal (rayo extraordinario) se refractarán hacia trayectorias algo diferentes. La luz natural, llamada luz no polarizada , consta de cantidades iguales de energía en dos polarizaciones ortogonales cualesquiera. Incluso la luz polarizada linealmente tiene algo de energía en ambas polarizaciones, a menos que esté alineada a lo largo de uno de los dos ejes de birrefringencia. Según la ley de refracción de Snell , los dos ángulos de refracción están regidos por el índice de refracción efectivo de cada una de estas dos polarizaciones. Esto se ve claramente, por ejemplo, en el prisma de Wollaston , que separa la luz entrante en dos polarizaciones lineales utilizando prismas compuestos de un material birrefringente como la calcita .
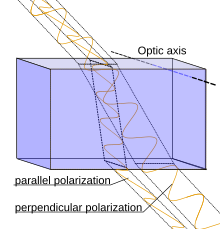
Los diferentes ángulos de refracción para los dos componentes de polarización se muestran en la figura en la parte superior de esta página, con el eje óptico a lo largo de la superficie (y perpendicular al plano de incidencia ), de modo que el ángulo de refracción es diferente para la polarización p (el "rayo ordinario" en este caso, que tiene su vector eléctrico perpendicular al eje óptico) y la polarización s (el "rayo extraordinario" en este caso, cuya polarización del campo eléctrico incluye un componente en la dirección del eje óptico). Además, se produce una forma distinta de doble refracción, incluso con incidencia normal, en los casos en que el eje óptico no está a lo largo de la superficie refractante (ni es exactamente normal a ella); en este caso, la polarización dieléctrica del material birrefringente no está exactamente en la dirección del campo eléctrico de la onda para el rayo extraordinario. La dirección del flujo de potencia (dada por el vector de Poynting ) para esta onda no homogénea está en un ángulo finito con respecto a la dirección del vector de onda, lo que resulta en una separación adicional entre estos rayos. Así, incluso en el caso de incidencia normal, en el que se calcularía el ángulo de refracción como cero (según la ley de Snell, independientemente del índice de refracción efectivo), la energía del rayo extraordinario se propaga en un ángulo. Si sale del cristal por una cara paralela a la cara entrante, se restablecerá la dirección de ambos rayos, pero dejando un desplazamiento entre los dos haces. Esto se observa comúnmente utilizando un trozo de calcita cortado a lo largo de su hendidura natural, colocado sobre un papel con escritura, como en las fotografías anteriores. Por el contrario, las placas de onda tienen específicamente su eje óptico a lo largo de la superficie de la placa, de modo que con una incidencia (aproximadamente) normal no habrá desplazamiento en la imagen de la luz de ninguna de las polarizaciones, simplemente un desplazamiento de fase relativo entre las dos ondas de luz.

Gran parte del trabajo sobre polarización precedió a la comprensión de la luz como una onda electromagnética transversal , y esto ha afectado a cierta terminología en uso. Los materiales isotrópicos tienen simetría en todas las direcciones y el índice de refracción es el mismo para cualquier dirección de polarización. Un material anisotrópico se llama "birrefringente" porque generalmente refractará un solo rayo entrante en dos direcciones, que ahora entendemos que corresponden a las dos polarizaciones diferentes. Esto es cierto tanto para un material uniaxial como para un biaxial.
En un material uniaxial, un rayo se comporta según la ley normal de refracción (que corresponde al índice de refracción ordinario), por lo que un rayo incidente con incidencia normal permanece normal a la superficie refractante. Como se explicó anteriormente, la otra polarización puede desviarse de la incidencia normal, lo que no se puede describir utilizando la ley de refracción. Por lo tanto, esto pasó a conocerse como el rayo extraordinario . Los términos "ordinario" y "extraordinario" todavía se aplican a los componentes de polarización perpendiculares y no perpendiculares al eje óptico respectivamente, incluso en los casos en que no hay doble refracción.
Un material se denomina uniaxial cuando tiene una única dirección de simetría en su comportamiento óptico, que llamamos eje óptico. También resulta ser el eje de simetría del elipsoide índice (un esferoide en este caso). El elipsoide índice podría describirse de acuerdo con los índices de refracción, n α , n β y n γ , a lo largo de tres ejes de coordenadas; en este caso dos son iguales. Entonces, si n α = n β correspondiente a los ejes x e y , entonces el índice extraordinario es n γ correspondiente al eje z , que también se llama eje óptico en este caso.
Los materiales en los que los tres índices de refracción son diferentes se denominan biaxiales , y el origen de este término es más complicado y a menudo se malinterpreta. En un cristal uniaxial, los diferentes componentes de polarización de un haz viajarán a diferentes velocidades de fase, excepto los rayos en la dirección de lo que llamamos el eje óptico. Por lo tanto, el eje óptico tiene la propiedad particular de que los rayos en esa dirección no exhiben birrefringencia, y todas las polarizaciones en dicho haz experimentan el mismo índice de refracción. Es muy diferente cuando los tres índices de refracción principales son todos diferentes; entonces, un rayo entrante en cualquiera de esas direcciones principales aún encontrará dos índices de refracción diferentes. Pero resulta que hay dos direcciones especiales (en un ángulo con respecto a los 3 ejes) donde los índices de refracción para diferentes polarizaciones son nuevamente iguales. Por esta razón, estos cristales se designaron como biaxiales , y los dos "ejes" en este caso se refieren a direcciones de rayos en las que la propagación no experimenta birrefringencia.
En un material birrefringente, una onda consta de dos componentes de polarización que generalmente están regidos por diferentes índices de refracción efectivos. El llamado rayo lento es el componente para el cual el material tiene el índice de refracción efectivo más alto (velocidad de fase más lenta), mientras que el rayo rápido es el que tiene un índice de refracción efectivo más bajo. Cuando un rayo incide sobre dicho material desde el aire (o cualquier material con un índice de refracción más bajo), el rayo lento se refracta más hacia la normal que el rayo rápido. En la figura de ejemplo en la parte superior de esta página, se puede ver que el rayo refractado con polarización s (con su vibración eléctrica a lo largo de la dirección del eje óptico, por lo tanto llamado rayo extraordinario [7] ) es el rayo lento en el escenario dado.
Utilizando una placa delgada de ese material con incidencia normal, se podría implementar una placa de onda . En este caso, no existe esencialmente separación espacial entre las polarizaciones, la fase de la onda en la polarización paralela (el rayo lento) estará retardada con respecto a la polarización perpendicular. Estas direcciones se conocen como eje lento y eje rápido de la placa de onda.
La birrefringencia uniaxial se clasifica como positiva cuando el índice extraordinario de refracción n e es mayor que el índice ordinario n o . La birrefringencia negativa significa que Δ n = n e − n o es menor que cero. [8] En otras palabras, la polarización de la onda rápida (o lenta) es perpendicular al eje óptico cuando la birrefringencia del cristal es positiva (o negativa, respectivamente). En el caso de los cristales biaxiales, los tres ejes principales tienen diferentes índices de refracción, por lo que esta designación no se aplica. Pero para cualquier dirección de rayo definida, también se pueden designar las polarizaciones de rayos rápidos y lentos.

Si bien la fuente más conocida de birrefringencia es la entrada de luz en un cristal anisotrópico, puede dar lugar a materiales ópticamente isotrópicos de varias maneras:

Los materiales birrefringentes mejor caracterizados son los cristales . Debido a sus estructuras cristalinas específicas , sus índices de refracción están bien definidos. Dependiendo de la simetría de una estructura cristalina (determinada por uno de los 32 grupos puntuales cristalográficos posibles ), los cristales de ese grupo pueden verse obligados a ser isotrópicos (no birrefringentes), a tener simetría uniaxial o a no tener ninguna de las dos, en cuyo caso se trata de un cristal biaxial. Las estructuras cristalinas que permiten la birrefringencia uniaxial y biaxial se indican en las dos tablas siguientes, que enumeran los dos o tres índices de refracción principales (a una longitud de onda de 590 nm) de algunos cristales más conocidos. [9]
Además de la birrefringencia inducida bajo tensión, muchos plásticos obtienen birrefringencia permanente durante la fabricación debido a tensiones que se "congelan" debido a las fuerzas mecánicas presentes cuando el plástico se moldea o se extruye. [10] Por ejemplo, el celofán común es birrefringente. Los polarizadores se utilizan rutinariamente para detectar la tensión, ya sea aplicada o congelada, en plásticos como el poliestireno y el policarbonato .
La fibra de algodón es birrefringente debido a los altos niveles de material celulósico en la pared celular secundaria de la fibra, que está alineada direccionalmente con las fibras de algodón.
La microscopía de luz polarizada se utiliza habitualmente en tejidos biológicos, ya que muchos materiales biológicos son birrefringentes lineal o circularmente. El colágeno, que se encuentra en el cartílago, los tendones, los huesos, las córneas y otras áreas del cuerpo, es birrefringente y se estudia habitualmente con microscopía de luz polarizada. [11] Algunas proteínas también son birrefringentes y presentan birrefringencia de forma. [12]
Las inevitables imperfecciones de fabricación en la fibra óptica conducen a la birrefringencia, que es una de las causas del ensanchamiento de los pulsos en las comunicaciones por fibra óptica . Estas imperfecciones pueden ser geométricas (falta de simetría circular) o debidas a una tensión lateral desigual aplicada a la fibra óptica. La birrefringencia se introduce intencionalmente (por ejemplo, haciendo que la sección transversal sea elíptica) para producir fibras ópticas que mantengan la polarización . La birrefringencia se puede inducir (o corregir) en las fibras ópticas doblándolas, lo que provoca anisotropía en la forma y la tensión dado el eje alrededor del cual se dobla y el radio de curvatura.
Además de la anisotropía en la polarizabilidad eléctrica que hemos estado analizando, la anisotropía en la permeabilidad magnética podría ser una fuente de birrefringencia. En frecuencias ópticas, no existe polarizabilidad magnética medible ( μ = μ 0 ) de los materiales naturales, por lo que no es una fuente real de birrefringencia. [ cita requerida ]
La birrefringencia y otros efectos ópticos basados en la polarización (como la rotación óptica y el dicroísmo lineal o circular ) se pueden observar midiendo cualquier cambio en la polarización de la luz que pasa a través del material. Estas mediciones se conocen como polarimetría . Los microscopios de luz polarizada, que contienen dos polarizadores que están a 90° entre sí a cada lado de la muestra, se utilizan para visualizar la birrefringencia, ya que la luz que no se ha visto afectada por la birrefringencia permanece en una polarización que es totalmente rechazada por el segundo polarizador ("analizador"). La adición de placas de cuarto de onda permite el examen utilizando luz polarizada circularmente. La determinación del cambio en el estado de polarización utilizando un aparato de este tipo es la base de la elipsometría , mediante la cual se pueden medir las propiedades ópticas de las superficies especulares a través de la reflexión.
Se han realizado mediciones de birrefringencia con sistemas modulados por fase para examinar el comportamiento transitorio del flujo de fluidos. [14] [15] La birrefringencia de las bicapas lipídicas se puede medir utilizando interferometría de polarización dual . Esto proporciona una medida del grado de orden dentro de estas capas de fluido y cómo se altera este orden cuando la capa interactúa con otras biomoléculas.
Para la medición 3D de la birrefringencia se puede utilizar una técnica basada en la tomografía holográfica [1].

La birrefringencia se utiliza en muchos dispositivos ópticos. Las pantallas de cristal líquido , el tipo más común de pantalla plana , hacen que sus píxeles se vuelvan más claros o más oscuros a través de la rotación de la polarización (birrefringencia circular) de la luz polarizada linealmente cuando se ve a través de un polarizador de lámina en la superficie de la pantalla. De manera similar, los moduladores de luz modulan la intensidad de la luz a través de la birrefringencia inducida eléctricamente de la luz polarizada seguida de un polarizador. El filtro Lyot es un filtro espectral de banda estrecha especializado que emplea la dependencia de la longitud de onda de la birrefringencia. Las placas de onda son láminas birrefringentes delgadas ampliamente utilizadas en ciertos equipos ópticos para modificar el estado de polarización de la luz que pasa a través de ellas.
Para fabricar polarizadores con alta transmitancia, se utilizan cristales birrefringentes en dispositivos como el prisma de Glan-Thompson , el prisma de Glan-Taylor y otras variantes. [16] También se pueden utilizar láminas de polímero birrefringentes en capas para este propósito. [17]
La birrefringencia también desempeña un papel importante en la generación de segundos armónicos y otros procesos ópticos no lineales . Los cristales utilizados para estos fines son casi siempre birrefringentes. Al ajustar el ángulo de incidencia, se puede ajustar el índice de refracción efectivo del rayo extraordinario para lograr la coincidencia de fase , que es necesaria para el funcionamiento eficiente de estos dispositivos.
La birrefringencia se utiliza en el diagnóstico médico. Un accesorio potente que se utiliza con los microscopios ópticos es un par de filtros polarizadores cruzados. La luz de la fuente se polariza en la dirección x después de pasar por el primer polarizador, pero encima de la muestra hay un polarizador (un llamado analizador ) orientado en la dirección y . Por lo tanto, el analizador no aceptará ninguna luz de la fuente y el campo aparecerá oscuro. Las áreas de la muestra que poseen birrefringencia generalmente acoplarán parte de la luz polarizada en x a la polarización y ; estas áreas aparecerán entonces brillantes contra el fondo oscuro. Las modificaciones a este principio básico pueden diferenciar entre birrefringencia positiva y negativa.
Por ejemplo, la aspiración con aguja del líquido de una articulación gotosa revelará cristales de urato monosódico con birrefringencia negativa . Los cristales de pirofosfato de calcio , por el contrario, muestran una birrefringencia positiva débil. [19] Los cristales de urato aparecen de color amarillo y los cristales de pirofosfato de calcio aparecen de color azul cuando sus ejes largos están alineados en paralelo al de un filtro compensador rojo, [20] o se añade a la muestra un cristal de birrefringencia conocida para comparar.
La birrefringencia del tejido dentro de un muslo humano vivo se midió utilizando tomografía de coherencia óptica sensible a la polarización a 1310 nm y una fibra monomodo en una aguja. La birrefringencia del músculo esquelético fue Δn = 1,79 × 10 −3 ± 0,18 × 10 −3 , adiposo Δn = 0,07 × 10 −3 ± 0,50 × 10 −3 , aponeurosis superficial Δn = 5,08 × 10 −3 ± 0,73 × 10 −3 y tejido intersticial Δn = 0,65 × 10 −3 ±0,39 × 10 −3 . [21] Estas mediciones pueden ser importantes para el desarrollo de un método menos invasivo para diagnosticar la distrofia muscular de Duchenne .
La birrefringencia se puede observar en placas amiloides como las que se encuentran en los cerebros de los pacientes con Alzheimer cuando se tiñen con un colorante como el Rojo Congo. Las proteínas modificadas, como las cadenas ligeras de inmunoglobulina, se acumulan de forma anormal entre las células y forman fibrillas. Múltiples pliegues de estas fibras se alinean y adoptan una conformación de lámina plegada en beta . El colorante Rojo Congo se intercala entre los pliegues y, cuando se observa bajo luz polarizada, provoca birrefringencia.
En oftalmología , la detección binocular de la birrefringencia retiniana de las fibras de Henle (axones de los fotorreceptores que salen radialmente de la fóvea) proporciona una detección fiable del estrabismo y posiblemente también de la ambliopía anisometrópica . [22] En sujetos sanos, el retraso máximo inducido por la capa de fibras de Henle es de aproximadamente 22 grados a 840 nm. [23] Además, la polarimetría láser de barrido utiliza la birrefringencia de la capa de fibras del nervio óptico para cuantificar indirectamente su espesor, lo que resulta útil en la evaluación y el seguimiento del glaucoma . Las mediciones de tomografía de coherencia óptica sensible a la polarización obtenidas de sujetos humanos sanos han demostrado un cambio en la birrefringencia de la capa de fibras del nervio óptico en función de la ubicación alrededor de la cabeza del nervio óptico. [24] La misma tecnología se aplicó recientemente en la retina humana viva para cuantificar las propiedades de polarización de las paredes de los vasos cerca del nervio óptico. [25] Mientras que las paredes de los vasos de la retina se vuelven más gruesas y menos birrefringentes en pacientes que sufren de hipertensión, [26] lo que indica una disminución en el estado de las paredes de los vasos, las paredes de los vasos de los pacientes diabéticos no experimentan un cambio en el grosor, pero sí ven un aumento en la birrefringencia, [27] presumiblemente debido a fibrosis o inflamación.
Las características de birrefringencia en las cabezas de los espermatozoides permiten la selección de espermatozoides para la inyección intracitoplasmática de espermatozoides . [28] Asimismo, la imagenología de la zona utiliza la birrefringencia en los ovocitos para seleccionar aquellos con mayores posibilidades de un embarazo exitoso. [29] La birrefringencia de partículas biopsiadas de nódulos pulmonares indica silicosis .
Los dermatólogos utilizan dermatoscopios para ver las lesiones cutáneas. Los dermatoscopios utilizan luz polarizada, lo que permite al usuario ver las estructuras cristalinas correspondientes al colágeno dérmico en la piel. Estas estructuras pueden aparecer como líneas blancas brillantes o formas de roseta y solo son visibles con dermatoscopia polarizada .

Los sólidos isótropos no presentan birrefringencia. Cuando están bajo tensión mecánica , se produce birrefringencia. La tensión se puede aplicar externamente o se "congela" después de que un artículo de plástico birrefringente se enfría después de su fabricación mediante moldeo por inyección . Cuando una muestra de este tipo se coloca entre dos polarizadores cruzados, se pueden observar patrones de color, porque la polarización de un rayo de luz gira después de pasar a través de un material birrefringente y la cantidad de rotación depende de la longitud de onda. El método experimental llamado fotoelasticidad utilizado para analizar la distribución de la tensión en sólidos se basa en el mismo principio. Ha habido investigaciones recientes sobre el uso de la birrefringencia inducida por tensión en una placa de vidrio para generar un vórtice óptico y haces de Poincaré completos (haces ópticos que tienen todos los estados de polarización posibles a lo largo de una sección transversal). [30]

La birrefringencia se observa en materiales elásticos anisotrópicos . En estos materiales, las dos polarizaciones se dividen según sus índices de refracción efectivos, que también son sensibles a la tensión.
El estudio de la birrefringencia en ondas transversales que viajan a través de la Tierra sólida (el núcleo líquido de la Tierra no admite ondas transversales) se utiliza ampliamente en sismología . [ cita requerida ]
La birrefringencia se utiliza ampliamente en mineralogía para identificar rocas, minerales y piedras preciosas. [ cita requerida ]
En un medio isotrópico (incluido el espacio libre), el llamado desplazamiento eléctrico ( D ) es proporcional al campo eléctrico ( E ) según D = ɛ E donde la permitividad del material ε es simplemente un escalar (e igual a n 2 ε 0 donde n es el índice de refracción ). En un material anisotrópico que exhibe birrefringencia, la relación entre D y E debe describirse ahora utilizando una ecuación tensorial :
donde ε es ahora un tensor de permitividad de 3 × 3. Suponemos linealidad y ausencia de permeabilidad magnética en el medio: μ = μ 0 . El campo eléctrico de una onda plana de frecuencia angular ω se puede escribir en la forma general:
donde r es el vector de posición, t es el tiempo y E 0 es un vector que describe el campo eléctrico en r = 0 , t = 0 . Luego encontraremos los posibles vectores de onda k . Combinando las ecuaciones de Maxwell para ∇ × E y ∇ × H , podemos eliminar H = 1/μ0 B para obtener:
Sin cargas libres, la ecuación de Maxwell para la divergencia de D se desvanece:
Podemos aplicar la identidad vectorial ∇ × (∇ × A ) = ∇(∇ ⋅ A ) − ∇ 2 A al lado izquierdo de la ecuación 3a y usar la dependencia espacial en la que cada diferenciación en x (por ejemplo) resulta en una multiplicación por ik x para encontrar:
El lado derecho de la ecuación 3a se puede expresar en términos de E mediante la aplicación del tensor de permitividad ε y observando que la diferenciación en el tiempo resulta en la multiplicación por − iω , la ecuación 3a se convierte entonces en:
Aplicando la regla de diferenciación a la ecuación 3b encontramos:
La ecuación 4b indica que D es ortogonal a la dirección del vector de onda k , aunque esto ya no es generalmente cierto para E, como sería el caso en un medio isotrópico. La ecuación 4b no será necesaria para los pasos posteriores de la siguiente derivación.
La forma más fácil de encontrar los valores permitidos de k para un ω dado es utilizando coordenadas cartesianas con los ejes x , y y z elegidos en las direcciones de los ejes de simetría del cristal (o simplemente eligiendo z en la dirección del eje óptico de un cristal uniaxial), lo que da como resultado una matriz diagonal para el tensor de permitividad ε :
donde los valores diagonales son cuadrados de los índices de refracción para polarizaciones a lo largo de los tres ejes principales x , y y z . Con ε en esta forma, y sustituyendo la velocidad de la luz c usando c 2 = 1/μ0 ε0 , el componente x de la ecuación vectorial ec. 4a se convierte en
donde E x , E y , E z son los componentes de E (en cualquier posición dada en el espacio y el tiempo) y k x , k y , k z son los componentes de k . Reordenando, podemos escribir (y de manera similar para los componentes y y z de la ecuación 4a )
Se trata de un conjunto de ecuaciones lineales en E x , E y , E z , por lo que puede tener una solución no trivial (es decir, una distinta de E = 0 ) siempre que el siguiente determinante sea cero:
Evaluando el determinante de la ecuación 6 y reordenando los términos según las potencias de , los términos constantes se cancelan. Después de eliminar el factor común de los términos restantes, obtenemos
En el caso de un material uniaxial, al elegir que el eje óptico esté en la dirección z de modo que n x = n y = n o y n z = n e , esta expresión se puede factorizar en
Fijando cualquiera de los factores en la ecuación 8 a cero se definirá una superficie elipsoidal [nota 1] en el espacio de vectores de onda k que están permitidos para un ω dado . El primer factor que es cero define una esfera; esta es la solución para los llamados rayos ordinarios, en los que el índice de refracción efectivo es exactamente n o independientemente de la dirección de k . El segundo define un esferoide simétrico respecto del eje z . Esta solución corresponde a los llamados rayos extraordinarios en los que el índice de refracción efectivo está entre n o y n e , dependiendo de la dirección de k . Por lo tanto, para cualquier dirección arbitraria de propagación (que no sea en la dirección del eje óptico), se permiten dos vectores de onda distintos k correspondientes a las polarizaciones de los rayos ordinarios y extraordinarios.
Para un material biaxial se puede describir una condición similar pero más complicada en las dos ondas; [31] el lugar geométrico de los vectores k permitidos (la superficie del vector de onda ) es una superficie de dos láminas de cuarto grado, de modo que en una dirección dada generalmente hay dos vectores k permitidos (y sus opuestos). [32] Mediante inspección se puede ver que la ecuación 6 se satisface generalmente para dos valores positivos de ω . O, para una frecuencia óptica especificada ω y una dirección normal a los frentes de onda a/| a | , se satisface para dos números de onda (o constantes de propagación) | k | (y por lo tanto índices de refracción efectivos) correspondientes a la propagación de dos polarizaciones lineales en esa dirección.
Cuando esas dos constantes de propagación son iguales, entonces el índice de refracción efectivo es independiente de la polarización y, en consecuencia, no hay birrefringencia encontrada por una onda que viaja en esa dirección particular. Para un cristal uniaxial, este es el eje óptico, la dirección ± z según la construcción anterior. Pero cuando los tres índices de refracción (o permitividades), n x , n y y n z son distintos, se puede demostrar que hay exactamente dos de esas direcciones, donde las dos láminas de la superficie del vector de onda se tocan; [32] estas direcciones no son en absoluto obvias y no se encuentran a lo largo de ninguno de los tres ejes principales ( x , y , z según la convención anterior). Históricamente, eso explica el uso del término "biaxial" para tales cristales, ya que la existencia de exactamente dos de esas direcciones especiales (consideradas "ejes") se descubrió mucho antes de que se entendieran físicamente la polarización y la birrefringencia. Estas dos direcciones especiales generalmente no son de particular interés; Los cristales biaxiales se caracterizan más bien por sus tres índices de refracción correspondientes a los tres ejes de simetría.
Un estado general de polarización lanzado al medio siempre se puede descomponer en dos ondas, una en cada una de esas dos polarizaciones, que se propagarán entonces con diferentes números de onda | k | . La aplicación de la diferente fase de propagación a esas dos ondas a lo largo de una distancia de propagación especificada dará como resultado un estado de polarización neta generalmente diferente en ese punto; este es el principio de la placa de onda , por ejemplo. Con una placa de onda, no hay desplazamiento espacial entre los dos rayos ya que sus vectores k siguen estando en la misma dirección. Esto es cierto cuando cada una de las dos polarizaciones es normal al eje óptico (el rayo ordinario) o paralela a él (el rayo extraordinario).
En el caso más general, existe una diferencia no sólo en la magnitud sino también en la dirección de los dos rayos. Por ejemplo, la fotografía a través de un cristal de calcita (arriba de la página) muestra una imagen desplazada en las dos polarizaciones; esto se debe a que el eje óptico no es paralelo ni normal a la superficie del cristal. E incluso cuando el eje óptico es paralelo a la superficie, esto ocurrirá para ondas lanzadas con una incidencia no normal (como se muestra en la figura explicativa). En estos casos, los dos vectores k se pueden encontrar resolviendo la ecuación 6 limitada por la condición de contorno que requiere que los componentes de los vectores k de las dos ondas transmitidas y el vector k de la onda incidente, tal como se proyecta sobre la superficie de la interfaz, deben ser todos idénticos. Para un cristal uniaxial se encontrará que no hay un desplazamiento espacial para el rayo ordinario (de ahí su nombre) que se refractará como si el material no fuera birrefringente con un índice igual a los dos ejes que no son el eje óptico. Para un cristal biaxial, ningún rayo se considera "ordinario" ni se refractaría generalmente de acuerdo con un índice de refracción igual a uno de los ejes principales.