Lemniscate constant

Ratio of the perimeter of Bernoulli's lemniscate to its diameter

Lemniscate of Bernoulli

In mathematics, the lemniscate constant ϖ is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter, analogous to the definition of π for the circle.^[1] Equivalently, the perimeter of the lemniscate ${\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}$ is 2ϖ. The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755.^[2] It also appears in evaluation of the gamma and beta function at certain rational values. The symbol ϖ is a cursive variant of π; see Pi § Variant pi.

Sometimes the quantities 2ϖ or ϖ/2 are referred to as the lemniscate constant.^[3][4]

As of 2024 over 1.2 trillion digits of this constant have been calculated.^[5]

History

Gauss's constant, denoted by G, is equal to ϖ /π ≈ 0.8346268^[6] and named after Carl Friedrich Gauss, who calculated it via the arithmetic–geometric mean as ${\displaystyle 1/M{\bigl (}1,{\sqrt {2}}{\bigr )}}$.^[7] By 1799, Gauss had two proofs of the theorem that ${\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}=\pi /\varpi }$ where ${\displaystyle \varpi }$ is the lemniscate constant.^[8]

John Todd named two more lemniscate constants, the first lemniscate constant A = ϖ/2 ≈ 1.3110287771 and the second lemniscate constant B = π/(2ϖ) ≈ 0.5990701173.^[9][10][11]

The lemniscate constant ${\displaystyle \varpi }$ and Todd's first lemniscate constant ${\displaystyle A}$ were proven transcendental by Carl Ludwig Siegel in 1932 and later by Theodor Schneider in 1937 and Todd's second lemniscate constant ${\displaystyle B}$ and Gauss's constant ${\displaystyle G}$ were proven transcendental by Theodor Schneider in 1941.^[9][12][13] In 1975, Gregory Chudnovsky proved that the set ${\displaystyle \{\pi ,\varpi \}}$ is algebraically independent over ${\displaystyle \mathbb {Q} }$, which implies that ${\displaystyle A}$ and ${\displaystyle B}$ are algebraically independent as well.^[14][15] But the set ${\displaystyle {\bigl \{}\pi ,M{\bigl (}1,1/{\sqrt {2}}{\bigr )},M'{\bigl (}1,1/{\sqrt {2}}{\bigr )}{\bigr \}}}$ (where the prime denotes the derivative with respect to the second variable) is not algebraically independent over ${\displaystyle \mathbb {Q} }$.^[16] In 1996, Yuri Nesterenko proved that the set ${\displaystyle \{\pi ,\varpi ,e^{\pi }\}}$ is algebraically independent over ${\displaystyle \mathbb {Q} }$.^[17]

Forms

Usually, ${\displaystyle \varpi }$ is defined by the first equality below, but it has many equivalent forms:^[18]

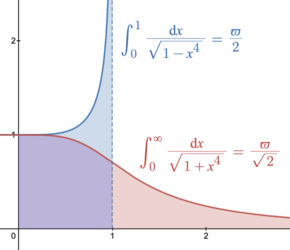
$${\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\tfrac {1}{2{\sqrt {2}}}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}$$

where K is the complete elliptic integral of the first kind with modulus k, Β is the beta function, Γ is the gamma function and ζ is the Riemann zeta function.

The lemniscate constant can also be computed by the arithmetic–geometric mean ${\displaystyle M}$,

$${\displaystyle \varpi ={\frac {\pi }{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}.}$$

Gauss's constant is typically defined as the reciprocal of the arithmetic–geometric mean of 1 and the square root of 2, after his calculation of ${\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}}$ published in 1800:^[19] $${\displaystyle G={\frac {1}{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}}$$John Todd's lemniscate constants may be given in terms of the beta function B: $${\displaystyle {\begin{aligned}A&={\frac {\varpi }{2}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )},\\[3mu]B&={\frac {\pi }{2\varpi }}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}}$$

As a special value of L-functions

$${\displaystyle \beta '(0)=\log {\frac {\varpi }{\sqrt {\pi }}}}$$

which is analogous to

$${\displaystyle \zeta '(0)=\log {\frac {1}{\sqrt {2\pi }}}}$$

where ${\displaystyle \beta }$ is the Dirichlet beta function and ${\displaystyle \zeta }$ is the Riemann zeta function.^[20]

Analogously to the Leibniz formula for π, $${\displaystyle \beta (1)=\sum _{n=1}^{\infty }{\frac {\chi (n)}{n}}={\frac {\pi }{4}},}$$we have^{[21][22][23][24][25]} $${\displaystyle L(E,1)=\sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}={\frac {\varpi }{4}}}$$where ${\displaystyle L}$ is the L-function of the elliptic curve ${\displaystyle E:\,y^{2}=x^{3}-x}$ over ${\displaystyle \mathbb {Q} }$; this means that ${\displaystyle \nu }$ is the multiplicative function given by $${\displaystyle \nu (p^{n})={\begin{cases}p-{\mathcal {N}}_{p},&p\in \mathbb {P} ,\,n=1\\[5mu]0,&p=2,\,n\geq 2\\[5mu]\nu (p)\nu (p^{n-1})-p\nu (p^{n-2}),&p\in \mathbb {P} \setminus \{2\},\,n\geq 2\end{cases}}}$$where ${\displaystyle {\mathcal {N}}_{p}}$ is the number of solutions of the congruence $${\displaystyle a^{3}-a\equiv b^{2}\,(\operatorname {mod} p),\quad p\in \mathbb {P} }$$in variables ${\displaystyle a,b}$ that are non-negative integers ( ${\displaystyle \mathbb {P} }$ is the set of all primes). Equivalently, ${\displaystyle \nu }$ is given by $${\displaystyle F(\tau )=\eta (4\tau )^{2}\eta (8\tau )^{2}=\sum _{n=1}^{\infty }\nu (n)q^{n},\quad q=e^{2\pi i\tau }}$$where ${\displaystyle \tau \in \mathbb {C} }$ such that ${\displaystyle \operatorname {\Im } \tau >0}$ and ${\displaystyle \eta }$ is the eta function.^[26][27][28]The above result can be equivalently written as $${\displaystyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}e^{-2\pi n/{\sqrt {32}}}={\frac {\varpi }{8}}}$$(the number ${\displaystyle 32}$ is the conductor of ${\displaystyle E}$) and also tells us that the BSD conjecture is true for the above ${\displaystyle E}$.^[29]The first few values of ${\displaystyle \nu }$ are given by the following table; if ${\displaystyle 1\leq n\leq 113}$ such that ${\displaystyle n}$ doesn't appear in the table, then ${\displaystyle \nu (n)=0}$: $${\displaystyle {\begin{array}{|c|c|c|c|}\hline n&\nu (n)&n&\nu (n)\\\hline 1&1&53&14\\\hline 5&-2&61&-10\\\hline 9&-3&65&-12\\\hline 13&6&73&-6\\\hline 17&2&81&9\\\hline 25&-1&85&-4\\\hline 29&-10&89&10\\\hline 37&-2&97&18\\\hline 41&10&101&-2\\\hline 45&6&109&6\\\hline 49&-7&113&-14\\\hline \end{array}}}$$

As a special value of other functions

Let ${\displaystyle \Delta }$ be the minimal weight level ${\displaystyle 1}$ new form. Then^[30] $${\displaystyle \Delta (i)={\frac {1}{64}}\left({\frac {\varpi }{\pi }}\right)^{12}.}$$The ${\displaystyle q}$-coefficient of ${\displaystyle \Delta }$ is the Ramanujan tau function.

Series

Viète's formula for π can be written:

$${\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }$$

An analogous formula for ϖ is:^[31]

$${\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }$$

The Wallis product for π is:

$${\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots }$$

An analogous formula for ϖ is:^[32]

$${\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots }$$

A related result for Gauss's constant ( ${\displaystyle G=\varpi /\pi }$) is:^[33]

$${\displaystyle {\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots }$$

An infinite series discovered by Gauss is:^[34]

$${\displaystyle {\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }$$

The Machin formula for π is ${\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}$ and several similar formulas for π can be developed using trigonometric angle sum identities, e.g. Euler's formula ${\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}$. Analogous formulas can be developed for ϖ, including the following found by Gauss: ${\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}}$, where ${\displaystyle \operatorname {arcsl} }$ is the lemniscate arcsine.^[35]

The lemniscate constant can be rapidly computed by the series^[36][37]

${\displaystyle \varpi =2^{-1/2}\pi {\biggl (}\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}{\biggr )}^{2}=2^{1/4}\pi e^{-\pi /12}{\biggl (}\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}{\biggr )}^{2}}$

where ${\displaystyle p_{n}={\tfrac {1}{2}}(3n^{2}-n)}$ (these are the generalized pentagonal numbers). Also^[38]

${\displaystyle \sum _{m,n\in \mathbb {Z} }e^{-2\pi (m^{2}+mn+n^{2})}={\sqrt {1+{\sqrt {3}}}}{\dfrac {\varpi }{12^{1/8}\pi }}.}$

In a spirit similar to that of the Basel problem,

${\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}$

where ${\displaystyle \mathbb {Z} [i]}$ are the Gaussian integers and ${\displaystyle G_{4}}$ is the Eisenstein series of weight ⁠ ${\displaystyle 4}$⁠ (see Lemniscate elliptic functions § Hurwitz numbers for a more general result).^[39]

A related result is

${\displaystyle \sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}}$

where ${\displaystyle \sigma _{3}}$ is the sum of positive divisors function.^[40]

In 1842, Malmsten found

${\displaystyle \beta '(1)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)}$

where ${\displaystyle \gamma }$ is Euler's constant and ${\displaystyle \beta (s)}$ is the Dirichlet-Beta function.

The lemniscate constant is given by the rapidly converging series

$${\displaystyle \varpi =\pi {\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}{\biggl (}\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}{\biggr )}^{2}.}$$

The constant is also given by the infinite product

${\displaystyle \varpi =\pi \prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).}$

Also^[41]

${\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{6635520^{n}}}{\frac {(4n)!}{n!^{4}}}={\frac {24}{5^{7/4}}}{\frac {\varpi ^{2}}{\pi ^{2}}}.}$

Continued fractions

A (generalized) continued fraction for π is $${\displaystyle {\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}}$$An analogous formula for ϖ is^[10] $${\displaystyle {\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}}$$

Define Brouncker's continued fraction by^[42] $${\displaystyle b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.}$$Let ${\displaystyle n\geq 0}$ except for the first equality where ${\displaystyle n\geq 1}$. Then^[43][44] $${\displaystyle {\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}}$$For example, $${\displaystyle {\begin{aligned}b(1)&={\frac {4}{\pi }},&b(2)&={\frac {\varpi ^{2}}{\pi }},&b(3)&=\pi ,&b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}}$$

In fact, the values of ${\displaystyle b(1)}$ and ${\displaystyle b(2)}$, coupled with the functional equation $${\displaystyle b(s+2)={\frac {(s+1)^{2}}{b(s)}},}$$determine the values of ${\displaystyle b(n)}$ for all ${\displaystyle n}$.

Simple continued fractions

Simple continued fractions for the lemniscate constant and related constants include^[45][46] $${\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ],\\[8mu]2\varpi &=[5,4,10,2,1,2,3,29,\ldots ],\\[5mu]{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ],\\[2mu]{\frac {\varpi }{\pi }}&=[0,1,5,21,3,4,14,\ldots ].\end{aligned}}}$$

Integrals

A geometric representation of ${\displaystyle \varpi /2}$ and ${\displaystyle \varpi /{\sqrt {2}}}$

The lemniscate constant ϖ is related to the area under the curve ${\displaystyle x^{4}+y^{4}=1}$. Defining ${\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}}$, twice the area in the positive quadrant under the curve ${\displaystyle x^{n}+y^{n}=1}$ is ${\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}$ In the quartic case, ${\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}$

In 1842, Malmsten discovered that^[47]

$${\displaystyle \int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.}$$

Furthermore, $${\displaystyle \int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}}$$

and^[48]

$${\displaystyle \int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},}$$a form of Gaussian integral.

The lemniscate constant appears in the evaluation of the integrals

$${\displaystyle {\frac {\pi }{\varpi }}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx}$$

$${\displaystyle {\frac {\varpi }{\pi }}=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}}$$

John Todd's lemniscate constants are defined by integrals:^[9]

$${\displaystyle A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}$$

$${\displaystyle B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}$$

Circumference of an ellipse

The lemniscate constant satisfies the equation^[49]

$${\displaystyle {\frac {\pi }{\varpi }}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}$$

Euler discovered in 1738 that for the rectangular elastica (first and second lemniscate constants)^[50][49]

$${\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}$$

Now considering the circumference ${\displaystyle C}$ of the ellipse with axes ${\displaystyle {\sqrt {2}}}$ and ${\displaystyle 1}$, satisfying ${\displaystyle 2x^{2}+4y^{2}=1}$, Stirling noted that^[51]

$${\displaystyle {\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}$$

Hence the full circumference is

$${\displaystyle C={\frac {\pi }{\varpi }}+\varpi =3.820197789\ldots }$$

This is also the arc length of the sine curve on half a period:^[52]

$${\displaystyle C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx}$$

Other limits

Analogously to $${\displaystyle 2\pi =\lim _{n\to \infty }\left|{\frac {(2n)!}{\mathrm {B} _{2n}}}\right|^{\frac {1}{2n}}}$$where ${\displaystyle \mathrm {B} _{n}}$ are Bernoulli numbers, we have $${\displaystyle 2\varpi =\lim _{n\to \infty }\left({\frac {(4n)!}{\mathrm {H} _{4n}}}\right)^{\frac {1}{4n}}}$$where ${\displaystyle \mathrm {H} _{n}}$ are Hurwitz numbers.

Notes

1. See:
   • Gauss, C. F. (1866). Werke (Band III) (in Latin and German). Herausgegeben der Königlichen Gesellschaft der Wissenschaften zu Göttingen. p. 404
   • Cox 1984, p. 281
   • Eymard, Pierre; Lafon, Jean-Pierre (2004). The Number Pi. American Mathematical Society. ISBN 0-8218-3246-8. p. 199
   • Bottazzini, Umberto; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory. Springer. doi:10.1007/978-1-4614-5725-1. ISBN 978-1-4614-5724-4. p. 57
   • Arakawa, Tsuneo; Ibukiyama, Tomoyoshi; Kaneko, Masanobu (2014). Bernoulli Numbers and Zeta Functions. Springer. ISBN 978-4-431-54918-5. p. 203
2. See:
   • Finch 2003, p. 420
   • Kobayashi, Hiroyuki; Takeuchi, Shingo (2019), "Applications of generalized trigonometric functions with two parameters", Communications on Pure & Applied Analysis, 18 (3): 1509–1521, arXiv:1903.07407, doi:10.3934/cpaa.2019072, S2CID 102487670
   • Asai, Tetsuya (2007), Elliptic Gauss Sums and Hecke L-values at s=1, arXiv:0707.3711
   • "A062539 - Oeis".
3. "A064853 - Oeis".
4. "Lemniscate Constant".
5. "Records set by y-cruncher". numberworld.org. Retrieved 2024-08-20.
6. "A014549 - Oeis".
7. Finch 2003, p. 420.
8. Neither of these proofs was rigorous from the modern point of view. See Cox 1984, p. 281
9. Todd, John (January 1975). "The lemniscate constants". Communications of the ACM. 18 (1): 14–19. doi:10.1145/360569.360580. S2CID 85873.
10. "A085565 - Oeis". and "A076390 - Oeis".
11. Carlson, B. C. (2010), "Elliptic Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
12. In particular, Siegel proved that if ${\displaystyle \operatorname {G} _{4}(\omega _{1},\omega _{2})}$ and ${\displaystyle \operatorname {G} _{6}(\omega _{1},\omega _{2})}$ with ${\displaystyle \operatorname {Im} (\omega _{2}/\omega _{1})>0}$ are algebraic, then ${\displaystyle \omega _{1}}$ or ${\displaystyle \omega _{2}}$ is transcendental. Here, ${\displaystyle \operatorname {G} _{4}}$ and ${\displaystyle \operatorname {G} _{6}}$ are Eisenstein series. The fact that ${\displaystyle \varpi }$ is transcendental follows from ${\displaystyle \operatorname {G} _{4}(\varpi ,\varpi i)=1/15}$ and ${\displaystyle \operatorname {G} _{6}(\varpi ,\varpi i)=0.}$
    Apostol, T. M. (1990). Modular Functions and Dirichlet Series in Number Theory (Second ed.). Springer. p. 12. ISBN 0-387-97127-0.
    Siegel, C. L. (1932). "Über die Perioden elliptischer Funktionen". Journal für die reine und angewandte Mathematik (in German). 167: 62–69.
13. In particular, Schneider proved that the beta function ${\displaystyle \mathrm {B} (a,b)}$ is transcendental for all ${\displaystyle a,b\in \mathbb {Q} \setminus \mathbb {Z} }$ such that ${\displaystyle a+b\notin \mathbb {Z} _{0}^{-}}$. The fact that ${\displaystyle \varpi }$ is transcendental follows from ${\displaystyle \varpi ={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}}$ and similarly for B and G from ${\displaystyle \mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.}$
    Schneider, Theodor (1941). "Zur Theorie der Abelschen Funktionen und Integrale". Journal für die reine und angewandte Mathematik. 183 (19): 110–128. doi:10.1515/crll.1941.183.110. S2CID 118624331.
14. G. V. Choodnovsky: Algebraic independence of constants connected with the functions of analysis, Notices of the AMS 22, 1975, p. A-486
15. G. V. Chudnovsky: Contributions to The Theory of Transcendental Numbers, American Mathematical Society, 1984, p. 6
16. In fact, $${\displaystyle \pi =2{\sqrt {2}}{\frac {M^{3}\left(1,{\frac {1}{\sqrt {2}}}\right)}{M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}={\frac {1}{G^{3}M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}.}$$
    Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience. ISBN 0-471-83138-7. p. 45
17. Nesterenko, Y. V.; Philippon, P. (2001). Introduction to Algebraic Independence Theory. Springer. p. 27. ISBN 3-540-41496-7.
18. See:
    • Cox 1984, p. 281
    • Finch 2003, pp. 420–422
    • Schappacher, Norbert (1997). "Some milestones of lemniscatomy" (PDF). In Sertöz, S. (ed.). Algebraic Geometry (Proceedings of Bilkent Summer School, August 7–19, 1995, Ankara, Turkey). Marcel Dekker. pp. 257–290.
19. Cox 1984, p. 277.
20. "A113847 - Oeis".
21. Cremona, J. E. (1997). Algorithms for Modular Elliptic Curves (2nd ed.). Cambridge University Press. ISBN 0521598206. p. 31, formula (2.8.10)
22. In fact, the series ${\textstyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n^{s}}}}$ converges for ${\displaystyle \operatorname {\Re } s>5/6}$.
23. Murty, Vijaya Kumar (1995). Seminar on Fermat's Last Theorem. American Mathematical Society. p. 16. ISBN 9780821803134.
24. Cohen, Henri (1993). A Course in Computational Algebraic Number Theory. Springer-Verlag. p. 382–406. ISBN 978-3-642-08142-2.
25. "Elliptic curve with LMFDB label 32.a3 (Cremona label 32a2)". The L-functions and modular forms database.
26. The function ${\displaystyle F}$ is the unique weight ${\displaystyle 2}$ level ${\displaystyle 32}$ new form and it satisfies the functional equation

    ${\displaystyle F\left(-{\frac {1}{\tau }}\right)=-{\frac {\tau ^{2}}{32}}F\left({\frac {\tau {\vphantom {1}}}{32}}\right).}$

27. The ${\displaystyle \nu }$ function is closely related to the ${\displaystyle \xi }$ function which is the multiplicative function defined by

    ${\displaystyle \xi (p^{n})={\begin{cases}{\mathcal {N}}_{p}',&p\in \mathbb {P} ,\,n=1\\[5mu]\xi (p^{n-1})+\chi (p)^{n},&p\in \mathbb {P} ,\,n\geq 2\end{cases}}}$

    where ${\displaystyle {\mathcal {N}}_{p}'}$ is the number of solutions of the equation

    ${\displaystyle a^{2}+b^{2}=p,\quad p\in \mathbb {P} }$

    in variables ${\displaystyle a,b}$ that are non-negative integers (see Fermat's theorem on sums of two squares) and ${\displaystyle \chi }$ is the Dirichlet character from the Leibniz formula for π; also

    ${\displaystyle \sum _{d|n}\chi (d)=\xi (n)}$

    for any positive integer ${\displaystyle n}$ where the sum extends only over positive divisors; the relation between ${\displaystyle \nu }$ and ${\displaystyle \xi }$ is

    ${\displaystyle \sum _{k=0}^{n}(-1)^{k}\xi (4k+1)\xi (4n-4k+1)=\nu (2n+1)}$

    where ${\displaystyle n}$ is any non-negative integer.
28. The ${\displaystyle \nu }$ function also appears in

    ${\displaystyle \sum _{z\in \mathbb {G} ;\,z{\overline {z}}=n}z=\nu (n)}$

    where ${\displaystyle n}$ is any positive integer and ${\displaystyle \operatorname {\mathbb {G} } }$ is the set of all Gaussian integers of the form

    ${\displaystyle (-1)^{\frac {a\pm b-1}{2}}(a\pm bi)}$

    where ${\displaystyle a}$ is odd and ${\displaystyle b}$ is even. The ${\displaystyle \xi }$ function from the previous note satisfies

    ${\displaystyle \left|\{z:z\in \mathbb {G} \land z{\overline {z}}=n\}\right|=\xi (n)}$

    where ${\displaystyle n}$ is positive odd.
29. Rubin, Karl (1987). "Tate-Shafarevich groups and L-functions of elliptic curves with complex multiplication". Inventiones mathematicae. 89: 528.
30. "Newform orbit 1.12.a.a". The L-functions and modular forms database.
31. Levin (2006)
32. Hyde (2014) proves the validity of a more general Wallis-like formula for clover curves; here the special case of the lemniscate is slightly transformed, for clarity.
33. Hyde, Trevor (2014). "A Wallis product on clovers" (PDF). The American Mathematical Monthly. 121 (3): 237–243. doi:10.4169/amer.math.monthly.121.03.237. S2CID 34819500.
34. Bottazzini, Umberto; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory. Springer. doi:10.1007/978-1-4614-5725-1. ISBN 978-1-4614-5724-4. p. 60
35. Todd (1975)
36. Cox 1984, p. 307, eq. 2.21 for the first equality. The second equality can be proved by using the pentagonal number theorem.
37. Berndt, Bruce C. (1998). Ramanujan's Notebooks Part V. Springer. ISBN 978-1-4612-7221-2. p. 326
38. This formula can be proved by hypergeometric inversion: Let

    ${\displaystyle \operatorname {a} (q)=\sum _{m,n\in \mathbb {Z} }q^{m^{2}+mn+n^{2}}}$

    where ${\displaystyle q\in \mathbb {C} }$ with ${\displaystyle \left|q\right|<1}$. Then

    ${\displaystyle \operatorname {a} (q)={}_{2}F_{1}\left({\frac {1}{3}},{\frac {2}{3}},1,z\right)}$

    where

    ${\displaystyle q=\exp \left(-{\frac {2\pi }{\sqrt {3}}}{\frac {{}_{2}F_{1}(1/3,2/3,1,1-z)}{{}_{2}F_{1}(1/3,2/3,1,z)}}\right)}$

    where ${\displaystyle z\in \mathbb {C} \setminus \{0,1\}}$. The formula in question follows from setting ${\textstyle z={\tfrac {1}{4}}{\bigl (}3{\sqrt {3}}-5{\bigr )}}$.
39. Eymard, Pierre; Lafon, Jean-Pierre (2004). The Number Pi. American Mathematical Society. ISBN 0-8218-3246-8. p. 232
40. Garrett, Paul. "Level-one elliptic modular forms" (PDF). University of Minnesota. p. 11—13
41. The formula follows from the hypergeometric transformation

    ${\displaystyle {}_{3}F_{2}\left({\frac {1}{4}},{\frac {1}{2}},{\frac {3}{4}},1,1,16z{\frac {(1-z)^{2}}{(1+z)^{4}}}\right)=(1+z)\,{}_{2}F_{1}\left({\frac {1}{2}},{\frac {1}{2}},1,z\right)^{2}}$

    where ${\displaystyle z=\lambda (1+5i)}$ and ${\displaystyle \lambda }$ is the modular lambda function.
42. Khrushchev, Sergey (2008). Orthogonal Polynomials and Continued Fractions (First ed.). Cambridge University Press. ISBN 978-0-521-85419-1. p. 140 (eq. 3.34), p. 153. There's an error on p. 153: ${\displaystyle 4[\Gamma (3+s/4)/\Gamma (1+s/4)]^{2}}$ should be ${\displaystyle 4[\Gamma ((3+s)/4)/\Gamma ((1+s)/4)]^{2}}$.
43. Khrushchev, Sergey (2008). Orthogonal Polynomials and Continued Fractions (First ed.). Cambridge University Press. ISBN 978-0-521-85419-1. p. 146, 155
44. Perron, Oskar (1957). Die Lehre von den Kettenbrüchen: Band II (in German) (Third ed.). B. G. Teubner. p. 36, eq. 24
45. "A062540 - OEIS". oeis.org. Retrieved 2022-09-14.
46. "A053002 - OEIS". oeis.org.
47. Blagouchine, Iaroslav V. (2014). "Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results". The Ramanujan Journal. 35 (1): 21–110. doi:10.1007/s11139-013-9528-5. S2CID 120943474.
48. "A068467 - Oeis".
49. Cox 1984, p. 313.
50. Levien (2008)
51. Cox 1984, p. 312.
52. Adlaj, Semjon (2012). "An Eloquent Formula for the Perimeter of an Ellipse" (PDF). American Mathematical Society. p. 1097. One might also observe that the length of the "sine" curve over half a period, that is, the length of the graph of the function sin(t) from the point where t = 0 to the point where t = π , is ${\displaystyle {\sqrt {2}}l(1/{\sqrt {2}})=L+M}$. In this paper ${\displaystyle M=1/G=\pi /\varpi }$ and ${\displaystyle L=\pi /M=G\pi =\varpi }$.

References

• Weisstein, Eric W. "Lemniscate Constant". MathWorld.
• Sequences A014549, A053002, and A062539 in OEIS
• Cox, David A. (January 1984). "The Arithmetic-Geometric Mean of Gauss" (PDF). L'Enseignement Mathématique. 30 (2): 275–330. doi:10.5169/seals-53831. Retrieved 25 June 2022.
• Finch, Steven R. (18 August 2003). Mathematical Constants. Cambridge University Press. pp. 420–422. ISBN 978-0-521-81805-6.

External links

• "Gauss's constant and where it occurs". www.johndcook.com. 2021-10-17.