En la teoría de categorías , una rama de las matemáticas , el cono de un funtor es una noción abstracta que se utiliza para definir el límite de ese funtor . Los conos también aparecen en otras teorías de categorías.
Sea F : J → C un diagrama en C . Formalmente, un diagrama no es más que un funtor de J a C . El cambio en la terminología refleja el hecho de que pensamos en F como indexando una familia de objetos y morfismos en C . La categoría J se considera como una "categoría índice". Uno debería considerar esto en analogía con el concepto de una familia indexada de objetos en la teoría de conjuntos . La diferencia principal es que aquí también tenemos morfismos. Así, por ejemplo, cuando J es una categoría discreta , corresponde más estrechamente a la idea de una familia indexada en la teoría de conjuntos. Otro ejemplo común y más interesante toma a J como un espacio . J también puede tomarse como la categoría vacía, lo que lleva a los conos más simples.
Sea N un objeto de C. Un cono de N a F es una familia de morfismos.
para cada objeto X de J , tal que para cada morfismo f : X → Y en J el siguiente diagrama conmuta :
La colección (generalmente infinita) de todos estos triángulos se puede representar (parcialmente) en forma de un cono con vértice N. A veces se dice que el cono ψ tiene vértice N y base F.
También se puede definir la noción dual de un cono de F a N (también llamado cocono ) invirtiendo todas las flechas anteriores. Explícitamente, un cocono de F a N es una familia de morfismos.
para cada objeto X de J , tal que para cada morfismo f : X → Y en J el siguiente diagrama conmuta:
A primera vista, los conos parecen ser construcciones ligeramente anormales en la teoría de categorías. Son aplicaciones de un objeto a un funtor (o viceversa). En consonancia con el espíritu de la teoría de categorías, nos gustaría definirlos como morfismos u objetos en alguna categoría adecuada. De hecho, podemos hacer ambas cosas.
Sea J una categoría pequeña y sea C J la categoría de diagramas de tipo J en C (esto no es más que una categoría de funtores ). Definamos el funtor diagonal Δ : C → C J de la siguiente manera: Δ( N ) : J → C es el funtor constante para N para todo N en C .
Si F es un diagrama de tipo J en C , las siguientes afirmaciones son equivalentes:
Las afirmaciones duales también son equivalentes:
Todas estas afirmaciones se pueden verificar mediante una aplicación directa de las definiciones. Si consideramos los conos como transformaciones naturales, vemos que son simplemente morfismos en C J con un funtor constante como fuente (o destino).
Por lo anterior, podemos definir la categoría de conos a F como la categoría de coma (Δ ↓ F ). Los morfismos de conos son entonces simplemente morfismos en esta categoría. Esta equivalencia se basa en la observación de que una función natural entre funtores constantes Δ( N ), Δ( M ) corresponde a un morfismo entre N y M . En este sentido, el funtor diagonal actúa trivialmente sobre las flechas. De manera similar, escribir la definición de una función natural de un funtor constante Δ( N ) a F produce el mismo diagrama que el anterior. Como se podría esperar, un morfismo de un cono ( N , ψ) a un cono ( L , φ) es simplemente un morfismo N → L tal que todos los diagramas "obvios" conmutan (ver el primer diagrama en la siguiente sección).
Del mismo modo, la categoría de los cocos de F es la categoría de coma ( F ↓ Δ).
Los límites y colimites se definen como conos universales . Es decir, conos a través de los cuales se factorizan todos los demás conos. Un cono φ de L a F es un cono universal si para cualquier otro cono ψ de N a F existe un morfismo único de ψ a φ.
.svg/1280px-Functor_cone_(extended).svg.png)
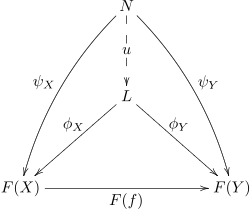
De manera equivalente, un cono universal a F es un morfismo universal de Δ a F (pensado como un objeto en C J ), o un objeto terminal en (Δ ↓ F ).
Dualmente, un cono φ de F a L es un cono universal si para cualquier otro cono ψ de F a N existe un morfismo único de φ a ψ.
.svg/1280px-Functor_co-cone_(extended).svg.png)
Equivalentemente, un cono universal de F es un morfismo universal de F a Δ, o un objeto inicial en ( F ↓ Δ).
El límite de F es un cono universal a F , y el colimite es un cono universal a partir de F . Como ocurre con todas las construcciones universales, no se garantiza que existan conos universales para todos los diagramas F , pero si existen son únicos hasta un isomorfismo único (en la categoría de coma (Δ ↓ F )).
