

Una matriz Halbach ( en alemán: [ˈhalbax] ) es una disposición especial de imanes permanentes que aumenta el campo magnético en un lado de la matriz mientras cancela el campo a casi cero en el otro lado. [1] [2] Esto se logra al tener un patrón de magnetización que gira espacialmente.
El patrón de rotación de los imanes permanentes (en la cara frontal; a la izquierda, arriba, derecha, abajo) puede continuar indefinidamente y tener el mismo efecto. El efecto de esta disposición es aproximadamente similar al de muchos imanes en forma de herradura colocados uno junto al otro, con polos similares en contacto.
Este proceso de orientación magnética replica el que se aplica mediante un cabezal de cinta de grabación magnética al revestimiento de la cinta magnética durante el proceso de grabación. El principio fue descrito con más detalle por James (Jim) M. Winey de Magnepan en 1970, para el caso ideal de magnetización en rotación continua, inducida por una bobina con forma de banda de un solo lado. [3]
El efecto también fue descubierto por John C. Mallinson en 1973, y estas estructuras de "flujo unilateral" fueron descritas inicialmente por él como una "curiosidad", aunque en ese momento reconoció a partir de este descubrimiento el potencial para mejoras significativas en la tecnología de la cinta magnética . [4]
El físico Klaus Halbach , mientras trabajaba en el Laboratorio Nacional Lawrence Berkeley durante la década de 1980, inventó de forma independiente el conjunto Halbach para enfocar los rayos del acelerador de partículas. [5]

Aunque esta distribución de flujo magnético parece algo contraintuitiva para aquellos familiarizados con simples imanes de barra o solenoides , la razón de esta distribución de flujo se puede visualizar intuitivamente utilizando el diagrama original de Mallinson (nótese que utiliza el componente y negativo , a diferencia del diagrama en el artículo de Mallinson). El diagrama muestra el campo de una tira de material ferromagnético con magnetización alternada en la dirección y (arriba a la izquierda) y en la dirección x (arriba a la derecha). Nótese que el campo sobre el plano está en la misma dirección para ambas estructuras, pero el campo debajo del plano está en direcciones opuestas . El efecto de superponer ambas estructuras se muestra en la figura.
El punto crucial es que el flujo se cancelará por debajo del plano y se reforzará por encima del plano . De hecho, cualquier patrón de magnetización en el que los componentes de la magnetización estén desfasados entre sí dará como resultado un flujo unilateral. La transformación matemática que desplaza la fase de todos los componentes de alguna función en se denomina transformada de Hilbert ; por lo tanto, los componentes del vector de magnetización pueden ser cualquier par de transformadas de Hilbert (la más simple de las cuales es simplemente , como se muestra en el diagrama anterior).

El campo en el lado no cancelante de la matriz ideal, infinita y que varía continuamente, tiene la forma [6]
dónde
Las ventajas de las distribuciones de flujo unilaterales son dobles:
Por lo tanto, tienen una sorprendente cantidad de aplicaciones, que van desde imanes de refrigerador planos , pasando por aplicaciones industriales como el motor de CC sin escobillas , bobinas móviles , [7] focalización magnética de fármacos [8] hasta aplicaciones de alta tecnología como imanes Wiggler utilizados en aceleradores de partículas y láseres de electrones libres .
El tren Maglev Inductrack [9] y el sistema de lanzamiento de cohetes Inductrack [10] utilizan el sistema Halbach para elevar el tren repeliendo los bucles de cable en la vía.

Los imanes de refrigerador planos y flexibles (no de ferrita cerámica dura ) se crean con un patrón de magnetización Halbach para una fuerza de sujeción más fuerte cuando se adhieren a una superficie ferromagnética plana (por ejemplo, la puerta de un refrigerador) que la fuerza de sujeción de una magnetización uniforme. Están hechos de ferrita en polvo mezclada en un aglutinante flexible (por ejemplo, plástico o caucho) que se expone a un patrón de campo de magnetización Halbach a medida que se extruye , lo que le da permanentemente a las partículas de ferrita en el compuesto magnético esta distribución de flujo unilateral (que se puede ver con una película de visualización magnética ).


Si ampliamos este diseño y añadimos una lámina superior, obtenemos un imán ondulador , que se utiliza en sincrotrones y láseres de electrones libres . Los imanes onduladores hacen oscilar un haz de electrones perpendicular al campo magnético. A medida que los electrones experimentan una aceleración, irradian energía electromagnética en su dirección de vuelo y, a medida que interactúan con la luz ya emitida, los fotones a lo largo de su línea se emiten en fase, lo que da como resultado un haz coherente y monocromático "similar a un láser".
El diseño que se muestra arriba se conoce generalmente como un ondulador de Halbach. Los vectores de magnetización en las láminas magnetizadas giran en sentidos opuestos entre sí; arriba, el vector de magnetización de la lámina superior gira en el sentido de las agujas del reloj y el vector de magnetización de la lámina inferior gira en el sentido contrario a las agujas del reloj. Este diseño se elige de modo que los componentes x de los campos magnéticos de las láminas se cancelen y los componentes y se refuercen, de modo que el campo esté dado por
donde k es el número de onda de la lámina magnética dado por el espaciamiento entre bloques magnéticos con el mismo vector de magnetización.


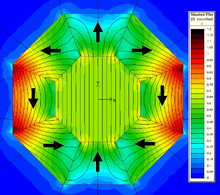
Se puede disponer una serie de barras magnéticas, magnetizadas perpendicularmente a sus ejes, en una matriz de Halbach. Si cada barra se gira alternativamente 90°, el campo resultante se mueve de un lado del plano de las barras al otro, como se muestra esquemáticamente en la figura.
Esta disposición permite que el campo se active y desactive de manera efectiva por encima o por debajo del plano de las varillas, dependiendo de la rotación de las varillas. Un dispositivo de este tipo constituye un pestillo magnético mecánico eficiente que no requiere energía. Un estudio detallado de esta disposición ha demostrado que cada varilla está sujeta a un fuerte par de torsión de sus varillas vecinas y, por lo tanto, requiere estabilización mecánica. [11] Sin embargo, una solución simple y eficiente, que proporciona tanto estabilización como la capacidad de girar cada varilla de manera alternativa, es simplemente proporcionar una disposición de engranajes iguales en cada varilla, como se muestra en la figura.

Un cilindro de Halbach es un cilindro magnetizado compuesto de material ferromagnético que produce (en el caso ideal) un campo magnético intenso confinado completamente dentro del cilindro, con un campo cero en el exterior. Los cilindros también pueden magnetizarse de manera que el campo magnético esté completamente fuera del cilindro, con un campo cero en el interior. En las figuras se muestran varias distribuciones de magnetización.
La dirección de magnetización dentro del material ferromagnético, en el plano perpendicular al eje del cilindro, está dada por
donde M r es la remanencia ferromagnética (A/m). Un valor positivo de k − 1 da un campo magnético interno y uno negativo da un campo magnético externo.
Lo ideal sería que estas estructuras se crearan a partir de un cilindro de material magnético de longitud infinita con una dirección de magnetización que variara continuamente. El flujo magnético producido por este diseño ideal sería perfectamente uniforme y estaría completamente confinado al interior del cilindro o al exterior del mismo. Por supuesto, el caso ideal de longitud infinita no es realizable y, en la práctica, la longitud finita de los cilindros produce efectos finales que introducen no uniformidades en el campo. [12] [13] La dificultad de fabricar un cilindro con una magnetización que varía continuamente también suele llevar a que el diseño se divida en segmentos.
Estas estructuras cilíndricas se utilizan en dispositivos como motores de CA sin escobillas, acoplamientos magnéticos y cilindros de alto campo. Tanto los motores sin escobillas como los dispositivos de acoplamiento utilizan disposiciones de campo multipolar:
Para el caso especial de k = 2, el campo dentro del orificio es uniforme y está dado por
donde los radios interior y exterior del cilindro son R i y R o respectivamente. H está en la dirección y . Esta es la forma más simple del cilindro de Halbach, y se puede ver que si la relación entre los radios exterior e interior es mayor que e , el flujo dentro del orificio en realidad excede la remanencia del material magnético utilizado para crear el cilindro. Sin embargo, se debe tener cuidado de no producir un campo que exceda la coercitividad de los imanes permanentes utilizados, ya que esto puede resultar en la desmagnetización del cilindro y la producción de un campo mucho menor que el previsto. [18] [19]

Este diseño cilíndrico es solo una clase de diseños que producen un campo uniforme dentro de una cavidad dentro de una matriz de imanes permanentes. Otras clases de diseño incluyen diseños de cuña, propuestos por Abele y Jensen, en los que se disponen cuñas de material magnetizado para proporcionar un campo uniforme dentro de las cavidades dentro del diseño, como se muestra.
La dirección de magnetización de las cuñas en (A) se puede calcular utilizando un conjunto de reglas dadas por Abele y permite una gran libertad en la forma de la cavidad. Otra clase de diseño es el mangle magnético (B), propuesto por Coey y Cugat, [20] [21] en el que las varillas magnetizadas uniformemente se disponen de tal manera que su magnetización coincida con la de un cilindro de Halbach, como se muestra para un diseño de 6 varillas. Este diseño aumenta en gran medida el acceso a la región de campo uniforme, a expensas de que el volumen de campo uniforme sea menor que en los diseños cilíndricos (aunque esta área se puede hacer más grande aumentando el número de varillas componentes). La rotación de las varillas entre sí da como resultado muchas posibilidades, incluido un campo variable dinámicamente y varias configuraciones dipolares. Se puede ver que los diseños mostrados en (A) y (B) están estrechamente relacionados con el cilindro de Halbach k = 2. Otros diseños muy simples para un campo uniforme incluyen imanes separados con caminos de retorno de hierro dulce, como se muestra en la figura (C).
En los últimos años, estos dipolos de Halbach se han utilizado para realizar experimentos de RMN de campo bajo . [22] En comparación con las geometrías de placa estándar (C) de imanes permanentes disponibles comercialmente ( Bruker Minispec), como se explicó anteriormente, ofrecen un diámetro de orificio enorme, al mismo tiempo que tienen un campo razonablemente homogéneo.
El método utilizado para encontrar el campo creado por el cilindro es matemáticamente muy similar al utilizado para investigar una esfera magnetizada uniformemente. [23]
Debido a la simetría de la disposición a lo largo del eje del cilindro, el problema puede tratarse como bidimensional. Trabaje en coordenadas plano-polares con vectores unitarios asociados y , y deje que el cilindro tenga una extensión radial . Entonces, la magnetización en las paredes del cilindro, que tiene una magnitud , gira suavemente como
mientras que la magnetización desaparece fuera de las paredes, es decir, dentro del pozo y sus alrededores .
Por definición, la intensidad del campo magnético auxiliar está relacionada con la magnetización y la densidad de flujo magnético mediante . Utilizando la ley de Gauss , esto es equivalente
Como el problema es estático, no hay corrientes libres y todas las derivadas temporales se anulan, por lo que la ley de Ampère requiere además , donde es el potencial escalar magnético (hasta un signo según algunas definiciones). Sustituyendo esto en la ecuación 1 anterior que rige y , encontramos que necesitamos resolver
que tiene la forma de la ecuación de Poisson .
Consideremos ahora las condiciones de contorno en las interfaces cilindro-aire y . La integración sobre un pequeño bucle que se extiende a ambos lados del límite y la aplicación del teorema de Stokes requiere que el componente paralelo de sea continuo. Esto, a su vez, requiere que sea continuo a través del límite. (Más propiamente, esto implica que deben diferir en una constante a través del límite, pero dado que las cantidades físicas que nos interesan dependen de gradientes de este potencial, podemos establecer arbitrariamente la constante en cero por conveniencia). Para obtener un segundo conjunto de condiciones, integre la ecuación 1 a través de un pequeño volumen que se extiende a ambos lados del límite y aplique el teorema de divergencia para encontrar
donde la notación denota un salto en la cantidad a través del límite, y en nuestro caso el signo es negativo en y positivo en . La diferencia de signo se debe a la orientación relativa de la magnetización y la superficie normal a la parte del volumen de integración dentro de las paredes del cilindro que son opuestas en los límites interno y externo.
En coordenadas plano-polares, la divergencia de un campo vectorial está dada por
De manera similar, el gradiente de un campo escalar está dado por
Combinando estas dos relaciones, el laplaciano se convierte en
Utilizando la ecuación 3 , la divergencia de magnetización en las paredes del cilindro es
Por lo tanto, la ecuación 2 , que es la que queremos resolver, se convierte en la ecuación 5.
Busque una solución particular de esta ecuación en las paredes del cilindro. Con el beneficio de la retrospectiva, considere , porque entonces tenemos
y también
Por lo tanto , y la comparación con la ecuación 6 muestra que es la solución particular apropiada.
Consideremos ahora la ecuación homogénea para la ecuación 6 , es decir , . Esta tiene la forma de la ecuación de Laplace . A través del método de separación de variables , se puede demostrar que la solución homogénea general cuyo gradiente es periódico en (de modo que todas las magnitudes físicas son univaluadas) está dada por
donde son constantes arbitrarias. La solución deseada será la suma de las soluciones particulares y homogéneas que satisfacen las condiciones de contorno. Nuevamente, con el beneficio de la retrospectiva, establezcamos la mayoría de las constantes en cero inmediatamente y afirmemos que la solución es
donde ahora hay constantes que deben determinarse. Si podemos elegir las constantes de manera que se satisfagan las condiciones de contorno, entonces, por el teorema de unicidad para la ecuación de Poisson , debemos haber encontrado la solución.
Las condiciones de continuidad dan
en el límite interior y
en el límite exterior. El gradiente de potencial tiene un componente radial que no desaparece en las paredes del cilindro y en el orificio, por lo que las condiciones de la derivada de potencial se convierten en
en el límite interior y
en el límite exterior. Nótese que estas son idénticas a las ecuaciones 7 y 8 , por lo que, de hecho, la suposición era consistente. Por lo tanto, tenemos y , lo que da la solución
En consecuencia, el campo magnético viene dado por
mientras que la densidad de flujo magnético se puede encontrar en todas partes utilizando la definición anterior . En el agujero, donde la magnetización desaparece, esto se reduce a . Por lo tanto, la magnitud de la densidad de flujo es
que es independiente de la posición. De manera similar, fuera del cilindro la magnetización también desaparece, y como el campo magnético desaparece allí, también lo hace la densidad de flujo. De modo que, efectivamente, el campo es uniforme dentro y cero fuera del cilindro ideal de Halbach, con una magnitud que depende de sus dimensiones físicas.
Los cilindros de Halbach generan un campo estático. Sin embargo, los cilindros pueden estar anidados y, al rotar un cilindro con respecto al otro, se puede lograr la cancelación del campo y el ajuste de la dirección. [24] Como el campo exterior de un cilindro es bastante bajo, la rotación relativa no requiere fuerzas fuertes. En el caso ideal de cilindros infinitamente largos, no se requeriría ninguna fuerza para rotar un cilindro con respecto al otro.

Si los patrones de distribución magnética bidimensionales del cilindro de Halbach se extienden a tres dimensiones, el resultado es la esfera de Halbach. Estos diseños tienen un campo extremadamente uniforme en el interior del diseño, ya que no se ven afectados por los "efectos finales" predominantes en el diseño de cilindros de longitud finita. La magnitud del campo uniforme para una esfera también aumenta a 4/3 de la cantidad para el diseño cilíndrico ideal con los mismos radios interno y externo. Sin embargo, para una estructura esférica, el acceso a la región del campo uniforme suele estar restringido a un orificio estrecho en la parte superior e inferior del diseño.
La ecuación para el campo en una esfera de Halbach es [25]
Se pueden lograr campos más altos optimizando el diseño esférico para tener en cuenta el hecho de que está compuesto de dipolos puntuales (y no dipolos lineales). Esto da como resultado el estiramiento de la esfera hasta una forma elíptica y una distribución no uniforme de la magnetización sobre las partes componentes. Usando este método, así como piezas polares blandas dentro del diseño, se logró 4,5 T en un volumen de trabajo de 20 mm 3 , [26] y esto se aumentó aún más a 5 T en 2002, [27] aunque sobre un volumen de trabajo más pequeño de 0,05 mm 3 . Como los materiales duros dependen de la temperatura, la refrigeración de todo el conjunto de imanes puede aumentar aún más el campo dentro del área de trabajo. Este grupo también informó sobre el desarrollo de un cilindro dipolar Halbach de 5,16 T en 2003. [28]
{{cite journal}}: Requiere citar revista |journal=( ayuda ){{cite journal}}: CS1 maint: multiple names: authors list (link){{cite journal}}: CS1 maint: multiple names: authors list (link)