Sobre (matemáticas)

Curva externa a una familia de curvas en geometría

Construcción de la envolvente de una familia de curvas.

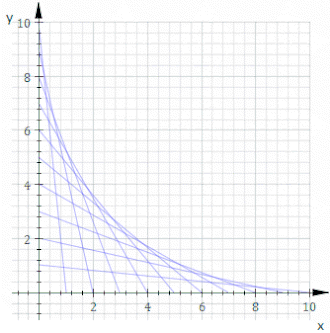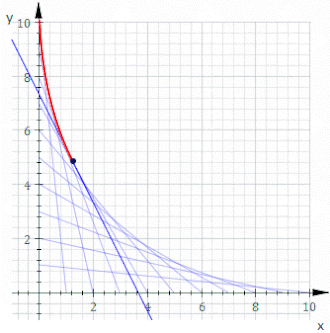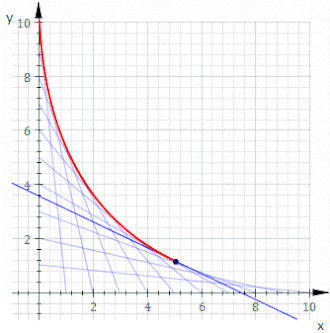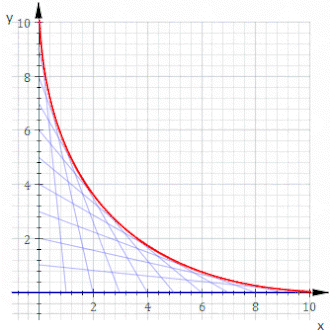
En geometría , una envolvente de una familia plana de curvas es una curva que es tangente a cada miembro de la familia en algún punto, y estos puntos de tangencia juntos forman la envolvente completa. Clásicamente, un punto de la envolvente puede considerarse como la intersección de dos curvas " infinitesimalmente adyacentes", es decir, el límite de las intersecciones de curvas cercanas. Esta idea se puede generalizar a una envolvente de superficies en el espacio, y así sucesivamente a dimensiones superiores.

Para que exista una envolvente, es necesario que los miembros individuales de la familia de curvas sean curvas diferenciables , ya que el concepto de tangencia no se aplica en caso contrario, y tiene que haber una transición suave a través de los miembros. Pero estas condiciones no son suficientes: una familia dada puede no tener envolvente. Un ejemplo sencillo de esto lo da una familia de círculos concéntricos de radio en expansión.

Envolvente de una familia de curvas

Sea cada curva C _t de la familia la solución de una ecuación f _t ( x ,  y )=0 (ver curva implícita ), donde t es un parámetro. Escriba F ( t ,  x ,  y )= f _t ( x ,  y ) y suponga que F es diferenciable.

La envolvente de la familia C _t se define entonces como el conjunto de puntos ( x , y ) para los cuales, simultáneamente, ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\partial F \over \partial t}(t,x,y)=0}$

para algún valor de t , donde es la derivada parcial de F con respecto a t . ^[1] ${\displaystyle \partial F/\partial t}$

Si t y u , t ≠ u son dos valores del parámetro entonces la intersección de las curvas C _t y C _u está dada por

${\displaystyle F(t,x,y)=F(u,x,y)=0\,}$

o, equivalentemente,

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.}$

Dejando u → t se obtiene la definición anterior.

Un caso especial importante es cuando F ( t ,  x ,  y ) es un polinomio en t . Esto incluye, despejando denominadores , el caso donde F ( t ,  x ,  y ) es una función racional en t . En este caso, la definición equivale a que t es una raíz doble de F ( t ,  x ,  y ), por lo que la ecuación de la envolvente se puede encontrar fijando el discriminante de F en 0 (porque la definición exige F = 0 en algún t y primera derivada = 0, es decir, su valor es 0 y es mín/máx en ese t).

Por ejemplo, sea C _t la línea cuyos puntos de corte en x e y son t y 11− t , como se muestra en la animación anterior. La ecuación de C _t es

${\displaystyle {\frac {x}{t}}+{\frac {y}{11-t}}=1}$

o, despejando fracciones,

${\displaystyle x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

La ecuación de la envolvente es entonces

${\displaystyle (-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+121=0.\,}$

A menudo, cuando F no es una función racional del parámetro, se puede reducir a este caso mediante una sustitución apropiada. Por ejemplo, si la familia está dada por C _θ con una ecuación de la forma u ( x ,  y )cos θ+ v ( x ,  y )sin θ= w ( x ,  y ), entonces al poner t = e ^{i θ} , cos θ=( t +1/ t )/2, sin θ=( t -1/ t )/2 i cambia la ecuación de la curva a

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w}$

o

${\displaystyle (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

La ecuación de la envolvente se obtiene entonces fijando el discriminante en 0:

${\displaystyle (u-iv)(u+iv)-w^{2}=0\,}$

o

${\displaystyle u^{2}+v^{2}=w^{2}.\,}$

Definiciones alternativas

1. La envolvente E ₁ es el límite de las intersecciones de las curvas cercanas C _t .
2. La envolvente E ₂ es una curva tangente a todos los C _t .
3. La envolvente E ₃ es el límite de la región rellena por las curvas C _t .

Entonces , y , donde es el conjunto de puntos definidos al comienzo de la sección padre de esta subsección. ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{2}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{3}\subseteq {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$

Ejemplos

Ejemplo 1

Estas definiciones E ₁ , E ₂ y E ₃ de la envolvente pueden ser conjuntos diferentes. Consideremos, por ejemplo, la curva y = x ³ parametrizada por γ : R → R ² donde γ( t ) = ( t , t ³ ) . La familia de curvas de un parámetro estará dada por las líneas tangentes a γ.

Primero calculamos el discriminante . La función generadora es ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,(x,y))=3t^{2}x-y-2t^{3}.}$

Calculando la derivada parcial F _t = 6 t ( x – t ) . Se deduce que o bien x = t o bien t = 0 . Supongamos primero que x = t y t ≠ 0 . Sustituyendo en F: y así, suponiendo que t ≠ 0, se deduce que F = F _t = 0 si y solo si ( x , y ) = ( t , t ³ ) . A continuación, suponiendo que t = 0 y sustituyendo en F se obtiene F (0,( x , y )) = − y . Por tanto, suponiendo que t = 0 , se deduce que F = F _t = 0 si y solo si y = 0 . Por tanto, el discriminante es la curva original y su línea tangente en γ(0): ${\displaystyle F(t,(t,y))=t^{3}-y\,}$

${\displaystyle {\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .}$

A continuación calculamos E ₁ . Una curva está dada por F ( t ,( x , y )) = 0 y una curva cercana está dada por F ( t + ε,( x , y )) donde ε es un número muy pequeño. El punto de intersección proviene de observar el límite de F ( t ,( x , y )) =  F ( t + ε,( x , y )) cuando ε tiende a cero. Observe que F ( t ,( x , y )) =  F ( t + ε,( x , y )) si y solo si

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Si t ≠ 0 entonces L tiene un único factor de ε. Suponiendo que t ≠ 0 entonces la intersección está dada por

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .}$

Como t ≠ 0 se deduce que x = t . El valor de y se calcula sabiendo que este punto debe estar en una línea tangente a la curva original γ: que F ( t ,( x , y )) = 0 . Sustituyendo y resolviendo se obtiene y = t ³ . Cuando t = 0 , L es divisible por ε ² . Suponiendo que t = 0 entonces la intersección está dada por

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .}$

De ello se deduce que x = 0 , y sabiendo que F ( t ,( x , y )) = 0 se obtiene y = 0 . De ello se deduce que

${\displaystyle E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

A continuación calculamos E ₂ . La curva en sí es la curva que es tangente a todas sus propias líneas tangentes. De ello se deduce que

${\displaystyle E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Finalmente calculamos E ₃ . Cada punto en el plano tiene al menos una línea tangente a γ que pasa por él, y por lo tanto la región llena por las líneas tangentes es todo el plano. El límite E ₃ es por lo tanto el conjunto vacío. De hecho, considere un punto en el plano, digamos ( x ₀ , y ₀ ). Este punto se encuentra en una línea tangente si y solo si existe un t tal que

${\displaystyle F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .}$

Esta es una cúbica en t y como tal tiene al menos una solución real. De ello se deduce que al menos una línea tangente a γ debe pasar por cualquier punto dado en el plano. Si y > x ³ e y > 0 entonces cada punto ( x , y ) tiene exactamente una línea tangente a γ que lo atraviesa. Lo mismo es cierto si y < x ³ y < 0 . Si y < x ³ e y > 0 entonces cada punto ( x , y ) tiene exactamente tres líneas tangentes distintas a γ que lo atraviesan. Lo mismo es cierto si y > x ³ e y < 0 . Si y = x ³ e y ≠ 0 entonces cada punto ( x , y ) tiene exactamente dos líneas tangentes a γ que lo atraviesan (esto corresponde a que la cúbica tiene una raíz ordinaria y una raíz repetida). Lo mismo es cierto si y ≠ x ³ e y = 0 . Si y = x ³ y x = 0 , es decir, x = y = 0 , entonces este punto tiene una sola línea tangente a γ que pasa por él (esto corresponde a la cúbica que tiene una raíz real de multiplicidad 3). De ello se deduce que

${\displaystyle E_{3}=\varnothing .}$

Ejemplo 2

Esta gráfica da la envolvente de la familia de líneas que unen los puntos ( t ,0), (0, k - t ), en la que k toma el valor 1.

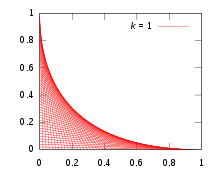
En el arte de cuerdas es común conectar de forma cruzada dos líneas de clavijas con la misma distancia entre sí. ¿Qué curva se forma?

Para simplificar, coloque los pines en los ejes x e y ; un diseño no ortogonal es una rotación y un escalado hacia afuera. Un hilo de línea recta general conecta los dos puntos (0, k − t ) y ( t , 0), donde k es una constante de escala arbitraria, y la familia de líneas se genera al variar el parámetro t . A partir de la geometría simple, la ecuación de esta línea recta es y = −( k  −  t ) x / t + k  −  t . Reordenando y convirtiendo en la forma F ( x , y , t ) = 0 se obtiene:

Ahora diferenciamos F ( x , y , t ) con respecto a t y fijamos el resultado igual a cero, para obtener

Estas dos ecuaciones definen conjuntamente la ecuación de la envolvente. De (2) tenemos:

${\displaystyle t={\sqrt {kx}}\,}$

Sustituyendo este valor de t en (1) y simplificando se obtiene una ecuación para la envolvente:

O bien, reordenándolo en una forma más elegante que muestre la simetría entre x e y:

Podemos tomar una rotación de los ejes donde el eje b es la línea y=x orientada al noreste y el eje a es la línea y =− x orientada al sureste. Estos nuevos ejes están relacionados con los ejes xy originales por x =( b + a )/ √ 2 e y =( b − a )/ √ 2 . Obtenemos, después de la sustitución en (4) y la expansión y simplificación,

que aparentemente es la ecuación de una parábola con eje a lo largo de a = 0, o y = x .

Ejemplo 3

Sea I ⊂ R un intervalo abierto y sea γ : I → R ² una curva plana suave parametrizada por la longitud de arco . Considérese la familia de un parámetro de rectas normales a γ( I ). Una recta es normal a γ en γ( t ) si pasa por γ( t ) y es perpendicular al vector tangente a γ en γ( t ). Sea T el vector tangente unitario a γ y sea N el vector normal unitario . Utilizando un punto para denotar el producto escalar , la familia generadora para la familia de un parámetro de rectas normales está dada por F  : I × R ² → R donde

${\displaystyle F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .}$

Claramente ( x − γ)· T = 0 si y solo si x − γ es perpendicular a T , o equivalentemente, si y solo si x − γ es paralelo a N , o equivalentemente, si y solo si x = γ + λ N para algún λ ∈ R . De ello se sigue que

${\displaystyle L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}}$

es exactamente la recta normal a γ en γ( t ₀ ). Para hallar el discriminante de F necesitamos calcular su derivada parcial con respecto a t :

${\displaystyle {\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,}$

donde κ es la curvatura de la curva plana de γ. Se ha visto que F = 0 si y sólo si x - γ = λ N para algún λ ∈ R . Suponiendo que F = 0 se obtiene

${\displaystyle {\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .}$

Suponiendo que κ ≠ 0 se deduce que λ = 1/κ y por lo tanto

${\displaystyle {\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .}$

Esta es exactamente la evolución de la curva γ.

Ejemplo 4

Una asteroide como envolvente de la familia de líneas que unen los puntos ( s ,0), (0, t ) con s ²  +  t ²  = 1

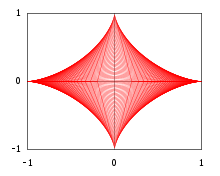
El siguiente ejemplo muestra que en algunos casos la envolvente de una familia de curvas puede verse como el límite topológico de una unión de conjuntos, cuyos límites son las curvas de la envolvente. Para y considérese el triángulo rectángulo (abierto) en un plano cartesiano con vértices , y ${\displaystyle s>0}$ ${\displaystyle t>0}$ ${\displaystyle (0,0)}$ ${\displaystyle (s,0)}$ ${\displaystyle (0,t)}$

${\displaystyle T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.}$

Fijemos un exponente y consideremos la unión de todos los triángulos sujetos a la restricción , es decir el conjunto abierto. ${\displaystyle \alpha >0}$ ${\displaystyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle \Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.}$

Para escribir una representación cartesiana de , comience con cualquier , que satisfaga y cualquier . La desigualdad de Hölder en con respecto a los exponentes conjugados y da: ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle s>0}$ ${\displaystyle \textstyle t>0}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$ ${\displaystyle \textstyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \mathbb {R} ^{2}}$ ${\displaystyle p:=1+{\frac {1}{\alpha }}}$ ${\displaystyle \textstyle q:={1+\alpha }}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}}$,

con igualdad si y sólo si . En términos de una unión de conjuntos la última desigualdad se lee: el punto pertenece al conjunto , es decir, pertenece a algún con , si y sólo si satisface ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$ ${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.}$

Además, el límite del conjunto es la envolvente de la familia correspondiente de segmentos de línea. ${\displaystyle \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$

${\displaystyle \left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(es decir, las hipotenusas de los triángulos), y tiene ecuación cartesiana

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.}$

Nótese que, en particular, el valor da el arco de parábola del Ejemplo 2, y el valor (lo que significa que todas las hipotenusas son segmentos de longitud unitaria) da la astroide . ${\displaystyle \alpha =1}$ ${\displaystyle \alpha =2}$

Ejemplo 5

La envolvente de las órbitas de los proyectiles (con velocidad inicial constante) es una parábola cóncava. La velocidad inicial es de 10 m/s. Suponemos g = 10 m/s ² .

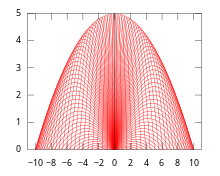
Consideremos el siguiente ejemplo de envolvente en movimiento. Supongamos que a una altura inicial 0 se lanza un proyectil al aire con una velocidad inicial constante v pero con diferentes ángulos de elevación θ. Sea x el eje horizontal en la superficie de movimiento y sea y el eje vertical. Entonces el movimiento da el siguiente sistema dinámico diferencial :

${\displaystyle {\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0,}$

que satisface cuatro condiciones iniciales :

${\displaystyle {\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Aquí t denota el tiempo de movimiento, θ es el ángulo de elevación, g denota la aceleración gravitacional y v es la velocidad inicial constante (no la velocidad ). La solución del sistema anterior puede tomar una forma implícita :

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0.}$

Para encontrar su ecuación envolvente, se puede calcular la derivada deseada:

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.}$

Eliminando θ, se puede llegar a la siguiente ecuación de envolvente:

${\displaystyle y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.}$

Claramente la envolvente resultante también es una parábola cóncava .

Envolvente de una familia de superficies

Una familia de superficies de un parámetro en el espacio euclidiano tridimensional está dada por un conjunto de ecuaciones

${\displaystyle F(x,y,z,a)=0}$

dependiendo de un parámetro real a . ^[2] Por ejemplo, los planos tangentes a una superficie a lo largo de una curva en la superficie forman dicha familia.

Dos superficies correspondientes a diferentes valores a y a' se intersecan en una curva común definida por

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.}$

En el límite, cuando a' se aproxima a a , esta curva tiende a una curva contenida en la superficie en a

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

Esta curva se denomina característica de la familia en a . A medida que a varía el lugar geométrico de estas curvas características se define una superficie denominada envolvente de la familia de superficies.

La envolvente de una familia de superficies es tangente a cada superficie de la familia a lo largo de la curva característica de esa superficie.

Generalizaciones

La idea de una envolvente de una familia de subvariedades suaves se desprende de manera natural. En general, si tenemos una familia de subvariedades con codimensión c , entonces necesitamos tener al menos una familia de c parámetros de dichas subvariedades. Por ejemplo: una familia de curvas de un parámetro en el espacio tridimensional ( c = 2) no tiene, genéricamente, una envolvente.

Aplicaciones

Ecuaciones diferenciales ordinarias

Las envolventes están relacionadas con el estudio de ecuaciones diferenciales ordinarias (EDO) y, en particular, soluciones singulares de EDO. ^[3] Consideremos, por ejemplo, la familia de un parámetro de líneas tangentes a la parábola y = x ² . Estas están dadas por la familia generadora F ( t ,( x , y )) = t ² – 2 tx + y . El conjunto de nivel cero F ( t ₀ ,( x , y )) = 0 da la ecuación de la línea tangente a la parábola en el punto ( t ₀ , t ₀ ² ). La ecuación t ² – 2 tx + y = 0 siempre se puede resolver para y como una función de x y, por lo tanto, considere

${\displaystyle t^{2}-2tx+y(x)=0.\ }$

Sustituyendo

${\displaystyle t=\left({\frac {dy}{dx}}\right)/2}$

da la ODE

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.}$

No es sorprendente que y  = 2 tx  −  t ² sean todas soluciones de esta EDO. Sin embargo, la envolvente de esta familia de líneas de un parámetro, que es la parábola y  =  x ² , también es una solución de esta EDO. Otro ejemplo famoso es la ecuación de Clairaut .

Ecuaciones diferenciales parciales

Las envolventes se pueden utilizar para construir soluciones más complicadas de ecuaciones diferenciales parciales (EDP) de primer orden a partir de otras más simples. ^[4] Sea F ( x , u , D u ) = 0 una EDP de primer orden, donde x es una variable con valores en un conjunto abierto Ω ⊂  R ⁿ , u es una función real desconocida, D u es el gradiente de u y F es una función continuamente diferenciable que es regular en D u . Supóngase que u ( x ; a ) es una familia de soluciones de m parámetros: es decir, para cada a  ∈  A  ⊂  R ^m fijo , u ( x ; a ) es una solución de la ecuación diferencial. Se puede construir una nueva solución de la ecuación diferencial resolviendo primero (si es posible)

${\displaystyle D_{a}u(x;a)=0\,}$

para a  = φ( x ) en función de x . La envolvente de la familia de funciones { u (·, a )} _{a ∈ A} se define por

${\displaystyle v(x)=u(x;\varphi (x)),\quad x\in \Omega ,}$

y también resuelve la ecuación diferencial (siempre que exista como una función continuamente diferenciable).

Geométricamente, el gráfico de v ( x ) es tangente en todas partes al gráfico de algún miembro de la familia u ( x ; a ). Dado que la ecuación diferencial es de primer orden, solo pone una condición en el plano tangente al gráfico, de modo que cualquier función tangente en todas partes a una solución también debe ser una solución. La misma idea subyace a la solución de una ecuación de primer orden como una integral del cono de Monge . ^[5] El cono de Monge es un campo de conos en el R ^{n +1} de las variables ( x , u ) recortado por la envolvente de los espacios tangentes a la EDP de primer orden en cada punto. Una solución de la EDP es entonces una envolvente del campo de conos.

En geometría de Riemann , si una familia de geodésicas suaves que pasan por un punto P en una variedad de Riemann tiene una envolvente, entonces P tiene un punto conjugado donde cualquier geodésica de la familia interseca la envolvente. Lo mismo es cierto de manera más general en el cálculo de variaciones : si una familia de extremales de un funcional que pasa por un punto dado P tiene una envolvente, entonces un punto donde un extremal interseca la envolvente es un punto conjugado a P.

Cáusticos

Cáustica reflectante generada a partir de un círculo y rayos paralelos

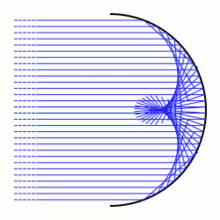
En óptica geométrica , una cáustica es la envoltura de una familia de rayos de luz . En esta imagen hay un arco de círculo. Los rayos de luz (mostrados en azul) provienen de una fuente en el infinito y, por lo tanto, llegan paralelos. Cuando inciden en el arco circular, los rayos de luz se dispersan en diferentes direcciones de acuerdo con la ley de reflexión . Cuando un rayo de luz incide en el arco en un punto, la luz se reflejará como si hubiera sido reflejada por la línea tangente del arco en ese punto. Los rayos de luz reflejados dan lugar a una familia de líneas de un parámetro en el plano. La envoltura de estas líneas es la cáustica reflectante . Una cáustica reflectante constará genéricamente de puntos lisos y puntos de cúspide ordinarios .

Desde el punto de vista del cálculo de variaciones, el principio de Fermat (en su forma moderna) implica que los rayos de luz son los extremos de la función de longitud.

${\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}$

entre curvas suaves γ en [ a , b ] con puntos finales fijos γ( a ) y γ( b ). La cáustica determinada por un punto dado P (en la imagen el punto está en el infinito) es el conjunto de puntos conjugados a P . ^[6]

Principio de Huygens

La luz puede atravesar medios anisotrópicos no homogéneos a distintas velocidades dependiendo de la dirección y la posición inicial de un rayo de luz. El límite del conjunto de puntos a los que la luz puede viajar desde un punto dado q después de un tiempo t se conoce como el frente de onda después del tiempo t , denotado aquí por Φ _q ( t ). Consiste precisamente en los puntos que se pueden alcanzar desde q en el tiempo t viajando a la velocidad de la luz. El principio de Huygens afirma que el conjunto de frentes de onda Φ _{q 0} ( s + t ) es la envolvente de la familia de frentes de onda Φ _q ( s ) para q  ∈ Φ _{q 0} ( t ). De manera más general, el punto q ₀ podría reemplazarse por cualquier curva, superficie o conjunto cerrado en el espacio. ^[7]

Véase también

• Cáustico (matemáticas)
• Teorema de la envolvente
• Superficie reglada

Referencias

1. Bruce, JW; Giblin, PJ (1984), Curvas y singularidades , Cambridge University Press, ISBN 0-521-42999-4
2. Eisenhart, Luther P. (2008), Un tratado sobre la geometría diferencial de curvas y superficies , Schwarz Press, ISBN 1-4437-3160-9
3. Forsyth, Andrew Russell (1959), Teoría de ecuaciones diferenciales , Seis volúmenes encuadernados en tres, Nueva York: Dover Publications , MR  0123757, §§100-106.
4. Evans, Lawrence C. (1998), Ecuaciones diferenciales parciales , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0772-9.
5. John, Fritz (1991), Ecuaciones diferenciales parciales (4.ª ed.), Springer, ISBN 978-0-387-90609-6.
6. Born, Max (octubre de 1999), Principio de óptica , Cambridge University Press , ISBN 978-0-521-64222-4Apéndice I: El cálculo de variaciones.
7. Arnold, VI (1997), Métodos matemáticos de la mecánica clásica, 2.ª ed. , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-96890-2, §46.

Enlaces externos

• Weisstein, Eric W. "Sobre". MathWorld .
• "Envolvente de una familia de curvas planas" en MathCurve.