Código de bloque

Familia de códigos de corrección de errores que codifican datos en bloques

En teoría de codificación , los códigos de bloque son una familia grande e importante de códigos de corrección de errores que codifican datos en bloques. Existe una gran cantidad de ejemplos de códigos de bloque, muchos de los cuales tienen una amplia gama de aplicaciones prácticas. La definición abstracta de códigos de bloque es conceptualmente útil porque permite a los teóricos de codificación, matemáticos y científicos informáticos estudiar las limitaciones de todos los códigos de bloque de una manera unificada. Dichas limitaciones a menudo toman la forma de límites que relacionan diferentes parámetros del código de bloque entre sí, como su velocidad y su capacidad para detectar y corregir errores.

Algunos ejemplos de códigos de bloque son los códigos Reed-Solomon , los códigos Hamming , los códigos Hadamard , los códigos Expander , los códigos Golay , los códigos Reed-Muller y los códigos Polares . Estos ejemplos también pertenecen a la clase de códigos lineales y, por lo tanto, se denominan códigos de bloque lineales . Más particularmente, estos códigos se conocen como códigos de bloque algebraicos o códigos de bloque cíclicos, porque se pueden generar utilizando polinomios booleanos.

Los códigos de bloques algebraicos suelen decodificarse de forma rígida mediante decodificadores algebraicos. ^{[ jerga ]}

El término código de bloque también puede referirse a cualquier código corrector de errores que actúa sobre un bloque de bits de datos de entrada para producir bits de datos de salida . En consecuencia, el codificador de bloques es un dispositivo sin memoria . Según esta definición, los códigos como los códigos turbo , los códigos convolucionales terminados y otros códigos iterativamente decodificables (códigos tipo turbo) también se considerarían códigos de bloque. Un codificador convolucional no terminado sería un ejemplo de un código sin bloques (sin marco), que tiene memoria y, en cambio, se clasifica como un código de árbol . ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle (n,k)}$

Este artículo trata sobre los "códigos de bloques algebraicos".

El código del bloque y sus parámetros

Los códigos de corrección de errores se utilizan para transmitir de forma fiable datos digitales a través de canales de comunicación poco fiables sujetos a ruido de canal . Cuando un emisor quiere transmitir un flujo de datos posiblemente muy largo utilizando un código de bloque, el emisor divide el flujo en fragmentos de un tamaño fijo. Cada uno de estos fragmentos se denomina mensaje y el procedimiento dado por el código de bloque codifica cada mensaje individualmente en una palabra de código, también llamada bloque en el contexto de los códigos de bloque. A continuación, el emisor transmite todos los bloques al receptor, que a su vez puede utilizar algún mecanismo de decodificación para (con suerte) recuperar los mensajes originales de los bloques recibidos posiblemente dañados. El rendimiento y el éxito de la transmisión general dependen de los parámetros del canal y del código de bloque.

Formalmente, un código de bloque es un mapeo inyectivo

${\displaystyle C:\Sigma ^{k}\to \Sigma ^{n}}$.

Aquí, es un conjunto finito y no vacío y y son números enteros. El significado y la importancia de estos tres parámetros y otros parámetros relacionados con el código se describen a continuación. ${\displaystyle \Sigma }$ ${\displaystyle k}$ ${\displaystyle n}$

El alfabeto Σ

El flujo de datos que se va a codificar se modela como una cadena sobre un alfabeto . El tamaño del alfabeto se escribe a menudo como . Si , entonces el código de bloque se denomina código de bloque binario . En muchas aplicaciones es útil considerar que es una potencia prima y se identifica con el campo finito . ${\displaystyle \Sigma }$ ${\displaystyle |\Sigma |}$ ${\displaystyle q}$ ${\displaystyle q=2}$ ${\displaystyle q}$ ${\displaystyle \Sigma }$ ${\displaystyle \mathbb {F} _{q}}$

La longitud del mensajea

Los mensajes son elementos de , es decir, cadenas de longitud . Por lo tanto, el número se denomina longitud del mensaje o dimensión de un código de bloque. ${\displaystyle m}$ ${\displaystyle \Sigma ^{k}}$ ${\displaystyle k}$ ${\displaystyle k}$

La longitud del bloquenorte

La longitud de bloque de un código de bloque es el número de símbolos en un bloque. Por lo tanto, los elementos de son cadenas de longitud y corresponden a bloques que pueden ser recibidos por el receptor. Por lo tanto, también se denominan palabras recibidas. Si para algún mensaje , entonces se denomina palabra de código de . ${\displaystyle n}$ ${\displaystyle c}$ ${\displaystyle \Sigma ^{n}}$ ${\displaystyle n}$ ${\displaystyle c=C(m)}$ ${\displaystyle m}$ ${\displaystyle c}$ ${\displaystyle m}$

La tasaR

La velocidad de un código de bloque se define como la relación entre la longitud de su mensaje y la longitud de su bloque:

${\displaystyle R=k/n}$.

Una tasa alta significa que la cantidad de mensajes reales por bloque transmitido es alta. En este sentido, la tasa mide la velocidad de transmisión y la cantidad mide la sobrecarga que se produce debido a la codificación con el código de bloque. Es un simple hecho teórico de la información que la tasa no puede exceder, ya que los datos en general no se pueden comprimir sin pérdidas. Formalmente, esto se deduce del hecho de que el código es un mapa inyectivo. ${\displaystyle 1-R}$ ${\displaystyle 1}$ ${\displaystyle C}$

La distanciad

La distancia o distancia mínima d de un código de bloque es el número mínimo de posiciones en las que difieren dos palabras de código distintas, y la distancia relativa es la fracción . Formalmente, para las palabras recibidas , sea la distancia de Hamming entre y , es decir, el número de posiciones en las que difieren y . Entonces la distancia mínima del código se define como ${\displaystyle \delta }$ ${\displaystyle d/n}$ ${\displaystyle c_{1},c_{2}\in \Sigma ^{n}}$ ${\displaystyle \Delta (c_{1},c_{2})}$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle d}$ ${\displaystyle C}$

${\displaystyle d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]}$.

Dado que cualquier código debe ser inyectivo , dos palabras de código cualesquiera no coincidirán en al menos una posición, por lo que la distancia de cualquier código es al menos . Además, la distancia es igual al peso mínimo para los códigos de bloque lineales porque: ${\displaystyle 1}$

${\displaystyle \min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [\mathbf {0} ,C(m_{1})+C(m_{2})]=\min _{m\in \Sigma ^{k} \atop m\neq \mathbf {0} }w[C(m)]=w_{\min }}$.

Una distancia mayor permite una mayor corrección y detección de errores. Por ejemplo, si solo consideramos los errores que pueden cambiar los símbolos de la palabra de código enviada pero nunca los borran o agregan, entonces el número de errores es el número de posiciones en las que difieren la palabra de código enviada y la palabra recibida. Un código con una distancia d permite al receptor detectar hasta errores de transmisión, ya que cambiar las posiciones de una palabra de código nunca puede generar accidentalmente otra palabra de código. Además, si no ocurren más de errores de transmisión, el receptor puede decodificar de forma única la palabra recibida en una palabra de código. Esto se debe a que cada palabra recibida tiene como máximo una palabra de código a una distancia . Si ocurren más de errores de transmisión, el receptor no puede decodificar de forma única la palabra recibida en general, ya que podría haber varias palabras de código posibles. Una forma en que el receptor puede hacer frente a esta situación es usar la decodificación de lista , en la que el decodificador genera una lista de todas las palabras de código en un radio determinado. ${\displaystyle d-1}$ ${\displaystyle d-1}$ ${\displaystyle (d-1)/2}$ ${\displaystyle (d-1)/2}$ ${\displaystyle (d-1)/2}$

Notación popular

La notación describe un código de bloque sobre un alfabeto de tamaño , con una longitud de bloque , una longitud de mensaje y una distancia . Si el código de bloque es un código de bloque lineal, se utilizan los corchetes en la notación para representar ese hecho. Para los códigos binarios con , a veces se omite el índice. Para los códigos separables con distancia máxima , la distancia siempre es , pero a veces no se conoce la distancia precisa, no es trivial de probar o enunciar, o no es necesaria. En tales casos, puede faltar el componente -. ${\displaystyle (n,k,d)_{q}}$ ${\displaystyle \Sigma }$ ${\displaystyle q}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle d}$ ${\displaystyle [n,k,d]_{q}}$ ${\displaystyle q=2}$ ${\displaystyle d=n-k+1}$ ${\displaystyle d}$

A veces, especialmente para códigos que no son de bloques, la notación se utiliza para códigos que contienen palabras de código de longitud . Para códigos de bloques con mensajes de longitud superior a un alfabeto de tamaño , este número sería . ${\displaystyle (n,M,d)_{q}}$ ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle q}$ ${\displaystyle M=q^{k}}$

Ejemplos

Como se mencionó anteriormente, existe una gran cantidad de códigos de corrección de errores que en realidad son códigos de bloque. El primer código de corrección de errores fue el código Hamming(7,4) , desarrollado por Richard W. Hamming en 1950. Este código transforma un mensaje que consta de 4 bits en una palabra de código de 7 bits agregando 3 bits de paridad. Por lo tanto, este código es un código de bloque. Resulta que también es un código lineal y que tiene una distancia de 3. En la notación abreviada anterior, esto significa que el código Hamming(7,4) es un código. ${\displaystyle [7,4,3]_{2}}$

Los códigos Reed-Solomon son una familia de códigos con y siendo una potencia principal . Los códigos de rango son una familia de códigos con . Los códigos Hadamard son una familia de códigos con y . ${\displaystyle [n,k,d]_{q}}$ ${\displaystyle d=n-k+1}$ ${\displaystyle q}$ ${\displaystyle [n,k,d]_{q}}$ ${\displaystyle d\leq n-k+1}$ ${\displaystyle [n,k,d]_{2}}$ ${\displaystyle n=2^{k-1}}$ ${\displaystyle d=2^{k-2}}$

Propiedades de detección y corrección de errores

Una palabra de código podría considerarse como un punto en el espacio de dimensión - y el código es el subconjunto de . Un código tiene distancia significa que , no hay otra palabra de código en la bola de Hamming centrada en con radio , que se define como la colección de palabras de dimensión - cuya distancia de Hamming a no es mayor que . De manera similar, con distancia (mínima) tiene las siguientes propiedades: ${\displaystyle c\in \Sigma ^{n}}$ ${\displaystyle n}$ ${\displaystyle \Sigma ^{n}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \Sigma ^{n}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle d}$ ${\displaystyle \forall c\in {\mathcal {C}}}$ ${\displaystyle c}$ ${\displaystyle d-1}$ ${\displaystyle n}$ ${\displaystyle c}$ ${\displaystyle d-1}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle d}$

• ${\displaystyle {\mathcal {C}}}$Puede detectar errores: debido a que una palabra de código es la única palabra de código en la bola de Hamming centrada en sí misma con un radio de , ningún patrón de error de o menos errores podrían cambiar una palabra de código a otra. Cuando el receptor detecta que el vector recibido no es una palabra de código de , se detectan los errores (pero no hay garantía de corregirlos). ${\displaystyle d-1}$ ${\displaystyle c}$ ${\displaystyle d-1}$ ${\displaystyle d-1}$ ${\displaystyle {\mathcal {C}}}$
• ${\displaystyle {\mathcal {C}}}$puede corregir errores. Debido a que una palabra de código es la única palabra de código en la bola de Hamming centrada en sí misma con un radio de , las dos bolas de Hamming centradas en dos palabras de código diferentes respectivamente con ambos radios no se superponen entre sí. Por lo tanto, si consideramos la corrección de errores como encontrar la palabra de código más cercana a la palabra recibida , siempre que el número de errores no sea mayor que , solo hay una palabra de código en la bola de Hamming centrada en con un radio de , por lo tanto, todos los errores podrían corregirse. ${\displaystyle \textstyle \left\lfloor {{d-1} \over 2}\right\rfloor }$ ${\displaystyle c}$ ${\displaystyle d-1}$ ${\displaystyle \textstyle \left\lfloor {{d-1} \over 2}\right\rfloor }$ ${\displaystyle y}$ ${\displaystyle \textstyle \left\lfloor {{d-1} \over 2}\right\rfloor }$ ${\displaystyle y}$ ${\displaystyle \textstyle \left\lfloor {{d-1} \over 2}\right\rfloor }$
• Para decodificar en presencia de más de errores, se puede utilizar la decodificación de lista o la decodificación de máxima verosimilitud . ${\displaystyle (d-1)/2}$
• ${\displaystyle {\mathcal {C}}}$Puede corregir borrones . Por borrón se entiende que se conoce la posición del símbolo borrado. La corrección se puede lograr mediante la decodificación de paso: al pasar, la posición borrada se llena con el símbolo y se realiza la corrección de errores. Debe haber un paso en el que el número de errores no sea mayor que y, por lo tanto, se puedan corregir los borrones. ${\displaystyle d-1}$ ${\displaystyle q}$ ${\displaystyle i^{th}}$ ${\displaystyle i^{th}}$ ${\displaystyle \textstyle \left\lfloor {{d-1} \over 2}\right\rfloor }$

Límites inferiores y superiores de los códigos de bloque

Límite de Hamming ^{[ aclaración necesaria ]}

Existen límites teóricos (como el límite de Hamming), pero otra cuestión es qué códigos se pueden construir realmente. ^{[ Aclaración necesaria ]} Es como meter esferas en una caja de muchas dimensiones. Este diagrama muestra los códigos que se pueden construir, que son lineales y binarios. El eje x muestra el número de símbolos protegidos k , el eje y el número de símbolos de control necesarios n–k . Se representan los límites para diferentes distancias de Hamming desde 1 (sin protección) hasta 34. Los códigos perfectos están marcados con puntos:

• naranja claro en el eje x : códigos triviales sin protección
• naranja en el eje y : códigos de repetición triviales
• naranja oscuro en el conjunto de datos d = 3: códigos de Hamming clásicos perfectos
• Rojo oscuro y más grande: el único código binario Golay perfecto

Familia de códigos

${\displaystyle C=\{C_{i}\}_{i\geq 1}}$se llama familia de códigos , donde es un código con monótona creciente . ${\displaystyle C_{i}}$ ${\displaystyle (n_{i},k_{i},d_{i})_{q}}$ ${\displaystyle n_{i}}$

La tasa de la familia de códigos C se define como ${\displaystyle R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}}$

La distancia relativa de la familia de códigos C se define como ${\displaystyle \delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}}$

Para explorar la relación entre y , se conoce un conjunto de límites inferior y superior de códigos de bloque. ${\displaystyle R(C)}$ ${\displaystyle \delta (C)}$

Hamming atado

${\displaystyle R\leq 1-{1 \over n}\cdot \log _{q}\cdot \left[\sum _{i=0}^{\left\lfloor {{\delta \cdot n-1} \over 2}\right\rfloor }{\binom {n}{i}}(q-1)^{i}\right]}$

Límite singleton

El límite Singleton es que la suma de la tasa y la distancia relativa de un código de bloque no puede ser mucho mayor que 1:

${\displaystyle R+\delta \leq 1+{\frac {1}{n}}}$.

En otras palabras, cada código de bloque satisface la desigualdad . Los códigos Reed-Solomon son ejemplos no triviales de códigos que satisfacen el límite singleton con igualdad. ${\displaystyle k+d\leq n+1}$

Plotkin atado

Para , . En otras palabras, . ${\displaystyle q=2}$ ${\displaystyle R+2\delta \leq 1}$ ${\displaystyle k+2d\leq n}$

Para el caso general, los siguientes límites de Plotkin se cumplen para cualquier distancia d : ${\displaystyle C\subseteq \mathbb {F} _{q}^{n}}$

1. Si ${\displaystyle d=\left(1-{1 \over q}\right)n,|C|\leq 2qn}$
2. Si ${\displaystyle d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}}$

Para cualquier código q -ario con distancia , ${\displaystyle \delta }$ ${\displaystyle R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)}$

Límite Gilbert-Varshamov

${\displaystyle R\geq 1-H_{q}\left(\delta \right)-\epsilon }$, donde , es la función de entropía q -aria. ${\displaystyle 0\leq \delta \leq 1-{1 \over q},0\leq \epsilon \leq 1-H_{q}\left(\delta \right)}$ ${\displaystyle H_{q}\left(x\right)~{\overset {\underset {\mathrm {def} }{}}{=}}~-x\cdot \log _{q}{x \over {q-1}}-\left(1-x\right)\cdot \log _{q}{\left(1-x\right)}}$

Johnson se dirige hacia

Defina . Sea el número máximo de palabras de código en una bola de Hamming de radio e para cualquier código de distancia d . ${\displaystyle J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)}$
${\displaystyle J_{q}\left(n,d,e\right)}$ ${\displaystyle C\subseteq \mathbb {F} _{q}^{n}}$

Entonces tenemos el límite de Johnson  : si ${\displaystyle J_{q}\left(n,d,e\right)\leq qnd}$ ${\displaystyle {e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)}$

Límite de Elias a Bassalygo

${\displaystyle R={\log _{q}{|C|} \over n}\leq 1-H_{q}\left(J_{q}\left(\delta \right)\right)+o\left(1\right)}$

Empaquetaduras y redes de esferas

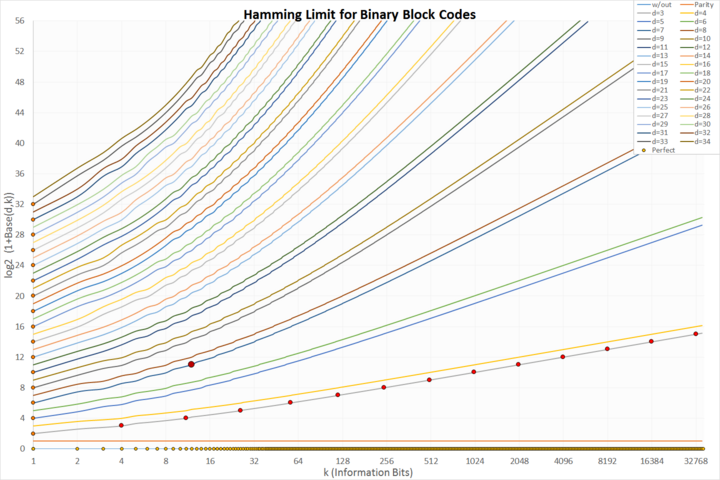
Los códigos de bloques están relacionados con el problema del empaquetamiento de esferas , que ha recibido cierta atención a lo largo de los años. En dos dimensiones, es fácil de visualizar. Tome un montón de monedas planas sobre la mesa y apriételas. El resultado es un patrón hexagonal como un nido de abejas. Pero los códigos de bloques dependen de más dimensiones que no se pueden visualizar fácilmente. El poderoso código Golay utilizado en las comunicaciones del espacio profundo utiliza 24 dimensiones. Si se utiliza como un código binario (que es lo que suele ser), las dimensiones se refieren a la longitud de la palabra clave como se definió anteriormente.

La teoría de la codificación utiliza el modelo de esfera de N dimensiones. Por ejemplo, ¿cuántas monedas se pueden colocar en un círculo sobre una mesa o, en tres dimensiones, cuántas canicas se pueden colocar en un globo terráqueo? Otras consideraciones entran en la elección de un código. Por ejemplo, el empaquetamiento de hexágonos en la restricción de una caja rectangular dejará espacio vacío en las esquinas. A medida que las dimensiones se hacen más grandes, el porcentaje de espacio vacío se hace más pequeño. Pero en ciertas dimensiones, el empaquetamiento utiliza todo el espacio y estos códigos son los llamados códigos perfectos. Hay muy pocos de estos códigos.

Otra propiedad es el número de vecinos que puede tener una sola palabra de código. ^[1] Nuevamente, considere los centavos como un ejemplo. Primero empaquetamos los centavos en una cuadrícula rectangular. Cada centavo tendrá 4 vecinos cercanos (y 4 en las esquinas que están más alejadas). En un hexágono, cada centavo tendrá 6 vecinos cercanos. Respectivamente, en tres y cuatro dimensiones, el empaquetamiento máximo está dado por las 12 caras y las 24 celdas con 12 y 24 vecinos, respectivamente. Cuando aumentamos las dimensiones, el número de vecinos cercanos aumenta muy rápidamente. En general, el valor está dado por los números de beso .

El resultado es que el número de formas en que el ruido puede hacer que el receptor elija un vecino (y por lo tanto un error) también aumenta. Esta es una limitación fundamental de los códigos de bloque y, de hecho, de todos los códigos. Puede ser más difícil provocar un error en un solo vecino, pero el número de vecinos puede ser lo suficientemente grande como para que la probabilidad total de error realmente se vea afectada. ^[1]

Véase también

• Capacidad del canal
• Teorema de Shannon-Hartley
• Canal ruidoso
• Descodificación de listas ^[1]
• Empaquetado de esferas

Referencias

1. Christian Schlegel y Lance Pérez (2004). Codificación enrejada y turbo. Wiley-IEEE. p. 73. ISBN 978-0-471-22755-7.

• JH van Lint (1992). Introducción a la teoría de la codificación. GTM . Vol. 86 (2.ª ed.). Springer-Verlag. pág. 31. ISBN. 3-540-54894-7.
• FJ MacWilliams ; NJA Sloane (1977). La teoría de los códigos de corrección de errores . Holanda septentrional. pág. 35. ISBN 0-444-85193-3.
• W. Huffman; V. Pless (2003). Fundamentos de los códigos de corrección de errores . Cambridge University Press. ISBN 978-0-521-78280-7.
• S. Lin; DJ Jr. Costello (1983). Codificación de control de errores: fundamentos y aplicaciones . Prentice-Hall. ISBN 0-13-283796-X.

Enlaces externos

• Charan Langton (2001) Conceptos de codificación y codificación por bloques