código hadamard

Código de corrección de errores

Matriz del código Hadamard aumentado [32, 6, 16] para el código Reed-Muller (1, 5) de la sonda espacial de la NASA Mariner 9

Operaciones XOR
Aquí los campos blancos representan 0
y los campos rojos representan 1

El código Hadamard es un código de corrección de errores que lleva el nombre de Jacques Hadamard y que se utiliza para la detección y corrección de errores al transmitir mensajes a través de canales muy ruidosos o poco confiables. En 1971, el código se utilizó para transmitir fotografías de Marte a la Tierra desde la sonda espacial Mariner 9 de la NASA . ^[1] Debido a sus propiedades matemáticas únicas, el código Hadamard no solo es utilizado por ingenieros, sino que también se estudia intensamente en teoría de codificación , matemáticas e informática teórica . El código Hadamard también se conoce con los nombres de código Walsh , familia Walsh , ^[2] y código Walsh-Hadamard ^[3] en reconocimiento al matemático estadounidense Joseph Leonard Walsh .

El código Hadamard es un ejemplo de código lineal de longitud sobre un alfabeto binario . Desafortunadamente, este término es algo ambiguo ya que algunas referencias asumen una longitud de mensaje mientras que otras asumen una longitud de mensaje de . En este artículo, el primer caso se denomina código Hadamard mientras que el segundo se denomina código Hadamard aumentado . ${\displaystyle 2^{m}}$ ${\displaystyle k=m}$ ${\displaystyle k=m+1}$

El código Hadamard es único en el sentido de que cada palabra de código distinta de cero tiene un peso Hamming de exactamente , lo que implica que la distancia del código también es . En la notación estándar de la teoría de codificación para códigos de bloque , el código Hadamard es un código, es decir, es un código lineal sobre un alfabeto binario , tiene longitud de bloque , longitud (o dimensión) del mensaje y distancia mínima . La longitud del bloque es muy grande en comparación con la longitud del mensaje, pero por otro lado, los errores se pueden corregir incluso en condiciones extremadamente ruidosas. ${\displaystyle 2^{k-1}}$ ${\displaystyle 2^{k-1}}$ ${\displaystyle [2^{k},k,2^{k-1}]_{2}}$ ${\displaystyle 2^{k}}$ ${\displaystyle k}$ ${\displaystyle 2^{k}/2}$

El código Hadamard aumentado es una versión ligeramente mejorada del código Hadamard; es un código -y por lo tanto tiene una tasa ligeramente mejor manteniendo la distancia relativa de y, por lo tanto, se prefiere en aplicaciones prácticas. En teoría de la comunicación, esto se llama simplemente código Hadamard y es lo mismo que el código Reed-Muller de primer orden sobre el alfabeto binario. ^[4] ${\displaystyle [2^{k},k+1,2^{k-1}]_{2}}$ ${\displaystyle 1/2}$

Normalmente, los códigos de Hadamard se basan en la construcción de matrices de Hadamard de Sylvester , pero el término “código de Hadamard” también se utiliza para referirse a códigos construidos a partir de matrices de Hadamard arbitrarias , que no son necesariamente del tipo Sylvester. En general, dicho código no es lineal. Estos códigos fueron construidos por primera vez por Raj Chandra Bose y Sharadchandra Shankar Shrikhande en 1959. ^[5] Si n es el tamaño de la matriz de Hadamard, el código tiene parámetros , lo que significa que es un código binario no necesariamente lineal con 2 n palabras en código de longitud del bloque n y distancia mínima n /2. El esquema de construcción y decodificación que se describe a continuación se aplica para n general , pero la propiedad de linealidad y la identificación con los códigos de Reed-Muller requieren que n sea una potencia de 2 y que la matriz de Hadamard sea equivalente a la matriz construida por el método de Sylvester. ${\displaystyle (n,2n,n/2)_{2}}$

El código Hadamard es un código decodificable localmente , que proporciona una manera de recuperar partes del mensaje original con alta probabilidad, mirando solo una pequeña fracción de la palabra recibida. Esto da lugar a aplicaciones en la teoría de la complejidad computacional y particularmente en el diseño de pruebas comprobables probabilísticamente . Dado que la distancia relativa del código Hadamard es 1/2, normalmente sólo se puede esperar recuperarse de como máximo una fracción de 1/4 del error. Sin embargo, al utilizar la decodificación de listas , es posible calcular una lista corta de posibles mensajes candidatos siempre que se hayan dañado menos de los bits de la palabra recibida. ${\displaystyle {\frac {1}{2}}-\epsilon }$

En la comunicación de acceso múltiple por división de código (CDMA), el código Hadamard se conoce como Código Walsh y se utiliza para definir canales de comunicación individuales . Es habitual en la literatura CDMA referirse a las palabras clave como “códigos”. Cada usuario utilizará una palabra clave, o “código”, diferente para modular su señal. Debido a que las palabras de código Walsh son matemáticamente ortogonales , una señal codificada con Walsh aparece como ruido aleatorio para un terminal móvil con capacidad CDMA , a menos que ese terminal use la misma palabra de código que la utilizada para codificar la señal entrante . ^[6]

Historia

Código Hadamard es el nombre más comúnmente utilizado para este código en la literatura. Sin embargo, en el uso moderno, estos códigos de corrección de errores se denominan códigos Walsh-Hadamard.

Hay una razón para esto:

Jacques Hadamard no inventó el código él mismo, pero definió las matrices de Hadamard alrededor de 1893, mucho antes de que se desarrollara el primer código de corrección de errores , el código Hamming , en la década de 1940.

El código Hadamard se basa en matrices de Hadamard, y si bien hay muchas matrices de Hadamard diferentes que podrían usarse aquí, normalmente solo se usa la construcción de matrices de Hadamard de Sylvester para obtener las palabras clave del código Hadamard.

James Joseph Sylvester desarrolló su construcción de matrices de Hadamard en 1867, que en realidad es anterior al trabajo de Hadamard sobre matrices de Hadamard. De ahí que se discuta el nombre de código Hadamard y en ocasiones el código se llame código Walsh , en honor al matemático estadounidense Joseph Leonard Walsh .

Durante la misión Mariner 9 de 1971 se utilizó un código Hadamard aumentado para corregir errores de transmisión de imágenes. Los valores binarios utilizados durante esta misión tenían 6 bits de longitud, lo que representaba 64 valores en escala de grises .

Debido a las limitaciones de la calidad de la alineación del transmisor en ese momento (debido a problemas con el bucle de seguimiento Doppler), la longitud máxima de datos útil era de unos 30 bits. En lugar de utilizar un código de repetición , se utilizó un código Hadamard [32, 6, 16].

Con este esquema se pueden corregir errores de hasta 7 bits por palabra de 32 bits. En comparación con un código de 5 repeticiones , las propiedades de corrección de errores de este código Hadamard son mucho mejores, pero su tasa es comparable. El algoritmo de decodificación eficiente fue un factor importante en la decisión de utilizar este código.

El circuito utilizado se denominó "Máquina Verde". Empleó la transformada rápida de Fourier que puede aumentar la velocidad de decodificación en un factor de tres. Desde la década de 1990, el uso de este código por parte de los programas espaciales ha cesado más o menos, y la Red de Espacio Profundo de la NASA no admite este esquema de corrección de errores para sus antenas parabólicas de más de 26 m.

Construcciones

Si bien todos los códigos de Hadamard se basan en matrices de Hadamard, las construcciones difieren de manera sutil para diferentes campos científicos, autores y usos. Los ingenieros, que utilizan los códigos para la transmisión de datos, y los teóricos de la codificación , que analizan las propiedades extremas de los códigos, normalmente quieren que la velocidad del código sea lo más alta posible, incluso si esto significa que la construcción se vuelve matemáticamente un poco menos elegante.

Por otro lado, para muchas aplicaciones de los códigos Hadamard en informática teórica no es tan importante lograr la velocidad óptima y, por lo tanto, se prefieren construcciones más simples de códigos Hadamard, ya que pueden analizarse de manera más elegante.

Construcción utilizando productos internos.

Cuando se le da un mensaje binario de longitud , el código Hadamard codifica el mensaje en una palabra clave usando una función de codificación . Esta función hace uso del producto interno de dos vectores , que se define de la siguiente manera: ${\displaystyle x\in \{0,1\}^{k}}$ ${\displaystyle k}$ ${\displaystyle {\text{Had}}(x)}$ ${\displaystyle {\text{Had}}:\{0,1\}^{k}\to \{0,1\}^{2^{k}}.}$ ${\displaystyle \langle x,y\rangle }$ ${\displaystyle x,y\in \{0,1\}^{k}}$

${\displaystyle \langle x,y\rangle =\sum _{i=1}^{k}x_{i}y_{i}\ {\bmod {\ }}2\,.}$

Entonces la codificación de Hadamard se define como la secuencia de todos los productos internos con : ${\displaystyle x}$ ${\displaystyle x}$

${\displaystyle {\text{Had}}(x)={\Big (}\langle x,y\rangle {\Big )}_{y\in \{0,1\}^{k}}}$

Como se mencionó anteriormente, el código Hadamard aumentado se utiliza en la práctica ya que el código Hadamard en sí es algo derrochador. Esto se debe a que, si el primer bit de es cero, entonces el producto interno no contiene información alguna sobre y, por lo tanto, es imposible decodificar completamente solo a partir de esas posiciones de la palabra clave. Por otro lado, cuando la palabra clave está restringida a las posiciones donde , aún es posible decodificarla completamente . Por tanto, tiene sentido restringir el código Hadamard a estas posiciones, lo que da lugar a la codificación Hadamard aumentada de ; eso es, . ${\displaystyle y}$ ${\displaystyle y_{1}=0}$ ${\displaystyle x_{1}}$ ${\displaystyle x}$ ${\displaystyle y_{1}=1}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle {\text{pHad}}(x)={\Big (}\langle x,y\rangle {\Big )}_{y\in \{1\}\times \{0,1\}^{k-1}}}$

Construcción utilizando una matriz generadora.

El código Hadamard es un código lineal y todos los códigos lineales pueden generarse mediante una matriz generadora . Esta es una matriz que es válida para todos , donde el mensaje se ve como un vector fila y el producto vector-matriz se entiende en el espacio vectorial sobre el campo finito . En particular, surge una forma equivalente de escribir la definición del producto interno para el código Hadamard utilizando la matriz generadora cuyas columnas constan de todas las cadenas de longitud , es decir, ${\displaystyle G}$ ${\displaystyle {\text{Had}}(x)=x\cdot G}$ ${\displaystyle x\in \{0,1\}^{k}}$ ${\displaystyle x}$ ${\displaystyle \mathbb {F} _{2}}$ ${\displaystyle y}$ ${\displaystyle k}$

${\displaystyle G={\begin{pmatrix}\uparrow &\uparrow &&\uparrow \\y_{1}&y_{2}&\dots &y_{2^{k}}\\\downarrow &\downarrow &&\downarrow \end{pmatrix}}\,.}$

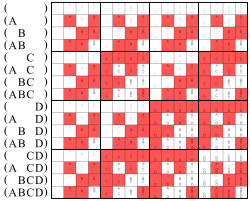
¿Dónde está el -ésimo vector binario en orden lexicográfico ? Por ejemplo, la matriz generadora del código de dimensión de Hadamard es: ${\displaystyle y_{i}\in \{0,1\}^{k}}$ ${\displaystyle i}$ ${\displaystyle k=3}$

${\displaystyle G={\begin{bmatrix}0&0&0&0&1&1&1&1\\0&0&1&1&0&0&1&1\\0&1&0&1&0&1&0&1\end{bmatrix}}.}$

La matriz es una matriz y da lugar al operador lineal . ${\displaystyle G}$ ${\displaystyle (k\times 2^{k})}$ ${\displaystyle {\text{Had}}:\{0,1\}^{k}\to \{0,1\}^{2^{k}}}$

La matriz generadora del código Hadamard aumentado se obtiene restringiendo la matriz a las columnas cuya primera entrada es uno. Por ejemplo, la matriz generadora del código de dimensión Hadamard aumentado es: ${\displaystyle G}$ ${\displaystyle k=3}$

${\displaystyle G'={\begin{bmatrix}1&1&1&1\\0&0&1&1\\0&1&0&1\end{bmatrix}}.}$

Entonces es un mapeo lineal con . ${\displaystyle {\text{pHad}}:\{0,1\}^{k}\to \{0,1\}^{2^{k-1}}}$ ${\displaystyle {\text{pHad}}(x)=x\cdot G'}$

En general , la matriz generadora del código Hadamard aumentado es una matriz de verificación de paridad para el código Hamming extendido de longitud y dimensión , lo que hace que el código Hadamard aumentado sea el código dual del código Hamming extendido. Por lo tanto, una forma alternativa de definir el código Hadamard es en términos de su matriz de verificación de paridad: la matriz de verificación de paridad del código Hadamard es igual a la matriz generadora del código Hamming. ${\displaystyle k}$ ${\displaystyle 2^{k-1}}$ ${\displaystyle 2^{k-1}-k}$

Construcción utilizando matrices generales de Hadamard.

Los códigos de Hadamard se obtienen a partir de una matriz de Hadamard H de n por n . En particular, las 2 n palabras de código del código son las filas de H y las filas de − H. Para obtener un código sobre el alfabeto {0,1}, se aplica la asignación −1 ↦ 1, 1 ↦ 0 o, de manera equivalente, x  ↦ (1 −  x )/2, a los elementos de la matriz. Que la distancia mínima del código es n /2 se desprende de la propiedad definitoria de las matrices de Hadamard, es decir, que sus filas son mutuamente ortogonales. Esto implica que dos filas distintas de una matriz de Hadamard difieren exactamente en n /2 posiciones y, dado que la negación de una fila no afecta la ortogonalidad, cualquier fila de H difiere de cualquier fila de − H en n /2 posiciones también, excepto cuando las filas corresponden, en cuyo caso difieren en n posiciones.

Para obtener el código Hadamard aumentado anterior con , la matriz Hadamard H elegida debe ser del tipo Sylvester, lo que da lugar a una longitud de mensaje de . ${\displaystyle n=2^{k-1}}$ ${\displaystyle \log _{2}(2n)=k}$

Distancia

La distancia de un código es la distancia mínima de Hamming entre dos palabras de código distintas cualesquiera, es decir, el número mínimo de posiciones en las que difieren dos palabras de código distintas. Dado que el código Walsh-Hadamard es un código lineal , la distancia es igual al peso mínimo de Hamming entre todas sus palabras en código distintas de cero. Todas las palabras en código distintas de cero del código Walsh-Hadamard tienen un peso Hamming de exactamente según el siguiente argumento. ${\displaystyle 2^{k-1}}$

Sea un mensaje distinto de cero. Entonces el siguiente valor es exactamente igual a la fracción de posiciones en la palabra clave que son iguales a uno: ${\displaystyle x\in \{0,1\}^{k}}$

${\displaystyle \Pr _{y\in \{0,1\}^{k}}{\big [}({\text{Had}}(x))_{y}=1{\big ]}=\Pr _{y\in \{0,1\}^{k}}{\big [}\langle x,y\rangle =1{\big ]}\,.}$

El hecho de que este último valor sea exacto se llama principio de subsuma aleatoria . Para ver que es cierto, supongamos sin pérdida de generalidad que . Entonces, cuando está condicionado a los valores de , el evento es equivalente a para algunos dependiendo de y . La probabilidad de que eso suceda es exactamente . Por lo tanto, de hecho, todas las palabras en código distintas de cero del código Hadamard tienen un peso relativo de Hamming y, por lo tanto, su distancia relativa es . ${\displaystyle 1/2}$ ${\displaystyle x_{1}=1}$ ${\displaystyle y_{2},\dots ,y_{k}}$ ${\displaystyle y_{1}\cdot x_{1}=b}$ ${\displaystyle b\in \{0,1\}}$ ${\displaystyle x_{2},\dots ,x_{k}}$ ${\displaystyle y_{2},\dots ,y_{k}}$ ${\displaystyle y_{1}=b}$ ${\displaystyle 1/2}$ ${\displaystyle 1/2}$ ${\displaystyle 1/2}$

La distancia relativa del código Hadamard aumentado también lo es, pero ya no tiene la propiedad de que cada palabra de código distinta de cero tenga peso exactamente ya que el vector all s es una palabra de código del código Hadamard aumentado. Esto se debe a que el vector codifica como . Además, siempre que sea distinto de cero y no sea el vector , se aplica nuevamente el principio de subsuma aleatoria y el peso relativo de es exactamente . ${\displaystyle 1/2}$ ${\displaystyle 1/2}$ ${\displaystyle 1}$ ${\displaystyle 1^{2^{k-1}}}$ ${\displaystyle x=10^{k-1}}$ ${\displaystyle {\text{pHad}}(10^{k-1})=1^{2^{k-1}}}$ ${\displaystyle x}$ ${\displaystyle 10^{k-1}}$ ${\displaystyle {\text{Had}}(x)}$ ${\displaystyle 1/2}$

Decodificabilidad local

Un código decodificable localmente es un código que permite recuperar un solo bit del mensaje original con alta probabilidad mirando solo una pequeña porción de la palabra recibida.

Un código es descodificable localmente si un bit de mensaje puede recuperarse comprobando los bits de la palabra recibida. Más formalmente, un código , es decodificable localmente, si existe un decodificador probabilístico, tal que (Nota: representa la distancia de Hamming entre los vectores y ) : ${\displaystyle q}$ ${\displaystyle x_{i}}$ ${\displaystyle q}$ ${\displaystyle C:\{0,1\}^{k}\rightarrow \{0,1\}^{n}}$ ${\displaystyle (q,\delta \geq 0,\epsilon \geq 0)}$ ${\displaystyle D:\{0,1\}^{n}\rightarrow \{0,1\}^{k}}$ ${\displaystyle \Delta (x,y)}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle \forall x\in \{0,1\}^{k},\forall y\in \{0,1\}^{n}}$, implica que ${\displaystyle \Delta (y,C(x))\leq \delta n}$ ${\displaystyle Pr[D(y)_{i}=x_{i}]\geq {\frac {1}{2}}+\epsilon ,\forall i\in [k]}$

Teorema 1: El código Walsh-Hadamard es localmente decodificable para todos . ${\displaystyle (2,\delta ,{\frac {1}{2}}-2\delta )}$ ${\displaystyle 0\leq \delta \leq {\frac {1}{4}}}$

Lema 1: Para todas las palabras de código, en un código Walsh-Hadamard, , , donde representan los bits en las posiciones y respectivamente, y representa el bit en la posición . ${\displaystyle c}$ ${\displaystyle C}$ ${\displaystyle c_{i}+c_{j}=c_{i+j}}$ ${\displaystyle c_{i},c_{j}}$ ${\displaystyle c}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle c_{i+j}}$ ${\displaystyle (i+j)}$

Prueba del lema 1

---

Sea la palabra clave correspondiente al mensaje . ${\displaystyle C(x)=c=(c_{0},\dots ,c_{2^{n}-1})}$ ${\displaystyle C}$ ${\displaystyle x}$

Sea la matriz generadora de . ${\displaystyle G={\begin{pmatrix}\uparrow &\uparrow &&\uparrow \\g_{0}&g_{1}&\dots &g_{2^{n}-1}\\\downarrow &\downarrow &&\downarrow \end{pmatrix}}}$ ${\displaystyle C}$

Por definición, . De esto, . Por la construcción de , . Por tanto, por sustitución, . ${\displaystyle c_{i}=x\cdot g_{i}}$ ${\displaystyle c_{i}+c_{j}=x\cdot g_{i}+x\cdot g_{j}=x\cdot (g_{i}+g_{j})}$ ${\displaystyle G}$ ${\displaystyle g_{i}+g_{j}=g_{i+j}}$ ${\displaystyle c_{i}+c_{j}=x\cdot g_{i+j}=c_{i+j}}$

Prueba del teorema 1

---

Para demostrar el teorema 1 construiremos un algoritmo de decodificación y demostraremos su exactitud.

Algoritmo

Entrada: palabra recibida ${\displaystyle y=(y_{0},\dots ,y_{2^{n}-1})}$

Para cada : ${\displaystyle i\in \{1,\dots ,n\}}$

1. Elija uniformemente al azar. ${\displaystyle j\in \{0,\dots ,2^{n}-1\}}$
2. Elija tal que , donde sea el -ésimo vector de base estándar y sea el xor bit a bit de y . ${\displaystyle k\in \{0,\dots ,2^{n}-1\}}$ ${\displaystyle j+k=e_{i}}$ ${\displaystyle e_{i}}$ ${\displaystyle i}$ ${\displaystyle j+k}$ ${\displaystyle j}$ ${\displaystyle k}$
3. ${\displaystyle x_{i}\gets y_{j}+y_{k}}$.

Salida: Mensaje ${\displaystyle x=(x_{1},\dots ,x_{n})}$

Prueba de corrección

Para cualquier mensaje, y una palabra recibida que difiera como máximo de una fracción de bits, se puede decodificar con una probabilidad de al menos . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle c=C(x)}$ ${\displaystyle \delta }$ ${\displaystyle x_{i}}$ ${\displaystyle {\frac {1}{2}}+({\frac {1}{2}}-2\delta )}$

Por el lema 1 ,. Dado que y se eligen de manera uniforme, la probabilidad de que sea como máximo . De manera similar, la probabilidad de que sea como máximo . Por el límite de unión , la probabilidad de que coincidan o no los bits correspondientes es como máximo . Si ambos y corresponden a , entonces se aplicará el lema 1 y, por lo tanto, se calculará el valor adecuado de. Por lo tanto, la probabilidad de que se decodifique correctamente es al menos . Por tanto, y para ser positivo, . ${\displaystyle c_{j}+c_{k}=c_{j+k}=x\cdot g_{j+k}=x\cdot e_{i}=x_{i}}$ ${\displaystyle j}$ ${\displaystyle k}$ ${\displaystyle y_{j}\not =c_{j}}$ ${\displaystyle \delta }$ ${\displaystyle y_{k}\not =c_{k}}$ ${\displaystyle \delta }$ ${\displaystyle y_{j}}$ ${\displaystyle y_{k}}$ ${\displaystyle c}$ ${\displaystyle 2\delta }$ ${\displaystyle y_{j}}$ ${\displaystyle y_{k}}$ ${\displaystyle c}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle 1-2\delta }$ ${\displaystyle \epsilon ={\frac {1}{2}}-2\delta }$ ${\displaystyle \epsilon }$ ${\displaystyle 0\leq \delta \leq {\frac {1}{4}}}$

Por lo tanto, el código Walsh-Hadamard es decodificable localmente para . ${\displaystyle (2,\delta ,{\frac {1}{2}}-2\delta )}$ ${\displaystyle 0\leq \delta \leq {\frac {1}{4}}}$

Optimidad

Para k  ≤ 7, los códigos lineales de Hadamard han demostrado ser óptimos en el sentido de distancia mínima. ^[7]

Ver también

• Secuencia Zadoff-Chu : mejora con respecto a los códigos Walsh-Hadamard

Referencias

1. Malek, Masoud (2006). "Códigos Hadarmark". Teoría de la codificación (PDF) . Archivado desde el original (PDF) el 9 de enero de 2020.
2. Amadeo, M.; Manzoli, Humberto; Merani, María Luisa (17 de noviembre de 2002). "Sobre la asignación de códigos Walsh y cuasi ortogonales en un sistema DS-CDMA multiportadora con múltiples clases de usuarios". Conferencia Mundial de Telecomunicaciones, 2002. GLOBECOM'02. IEEE . vol. 1. IEEE . págs. 841–845. doi :10.1109/GLOCOM.2002.1188196. ISBN 0-7803-7632-3.
3. Arora, Sanjeev ; Barac, Booz (2009). "Sección 19.2.2". Complejidad computacional: un enfoque moderno. Prensa de la Universidad de Cambridge . ISBN 978-0-521-42426-4.
4. Guruswami, Venkatesan (2009). Lista de decodificación de códigos binarios (PDF) . pag. 3.
5. Bosé, Raj Chandra ; Shrikhande, Sharadchandra Shankar (junio de 1959). "Una nota sobre un resultado en la teoría de la construcción de códigos". Información y Control . 2 (2): 183–194. CiteSeerX 10.1.1.154.2879 . doi :10.1016/S0019-9958(59)90376-6. 
6. Langton, Charan [en Wikidata] (2002). "Tutorial CDMA: Guía intuitiva de los principios de las comunicaciones" (PDF) . Complejo a Real. Archivado (PDF) desde el original el 20 de julio de 2011 . Consultado el 10 de noviembre de 2017 .
7. Jaffe, David B.; Bouyukliev, Iliya. "Códigos lineales binarios óptimos de dimensión como máximo siete". Archivado desde el original el 8 de agosto de 2007 . Consultado el 21 de agosto de 2007 .

Otras lecturas

• Rudra, Atri. "Código Hamming y encuadernación Hamming" (PDF) . Notas de lectura .
• Rudolph, Dietmar; Rudolph, Matías (12 de abril de 2011). "46.4. Códigos Hadamard o Walsh". Modulacionesverfahren (PDF) (en alemán). Cottbus, Alemania: Universidad Tecnológica de Brandeburgo (BTU). pag. 214. Archivado (PDF) desde el original el 16 de junio de 2021 . Consultado el 14 de junio de 2021 .(xiv+225 páginas)