Una estructura de árbol , diagrama de árbol o modelo de árbol es una forma de representar la naturaleza jerárquica de una estructura en forma gráfica. Se denomina "estructura de árbol" porque la representación clásica se asemeja a un árbol , aunque el diagrama generalmente está al revés en comparación con un árbol biológico, con el "tallo" en la parte superior y las "hojas" en la parte inferior.
Una estructura de árbol es conceptual y aparece en varias formas. Para una discusión de las estructuras de árbol en campos específicos, véase Árbol (estructura de datos) para informática; en la medida en que se relaciona con la teoría de grafos, véase árbol (teoría de grafos) o árbol (teoría de conjuntos) . A continuación se enumeran otros artículos relacionados.
Los elementos del árbol se denominan " nodos ". Las líneas que conectan los elementos se denominan "ramas". Los nodos sin hijos se denominan nodos hoja , "nodos finales" u "hojas".
Toda estructura de árbol finito tiene un miembro que no tiene un nodo superior . Este miembro se llama "raíz" o nodo raíz . La raíz es el nodo inicial. Pero lo inverso no es cierto: las estructuras de árbol infinitas pueden tener o no un nodo raíz.
Los nombres de las relaciones entre nodos modelan la terminología de parentesco de las relaciones familiares. Los nombres neutros en cuanto al género "padre" e "hijo" han desplazado en gran medida la terminología más antigua de "padre" e "hijo". El término "tío" todavía se utiliza ampliamente para otros nodos del mismo nivel que el padre, aunque a veces se reemplaza por términos neutros en cuanto al género como "ommer". [1]
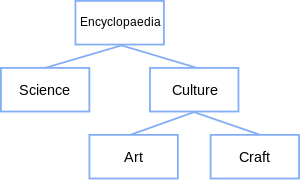
En el ejemplo, "enciclopedia" es el padre de "ciencia" y "cultura", sus hijos. "Arte" y "artesanía" son hermanos e hijos de "cultura", que es su padre y, por lo tanto, uno de sus antepasados. Además, "enciclopedia", como raíz del árbol, es el antepasado de "ciencia", "cultura", "arte" y "artesanía". Por último, "ciencia", "arte" y "artesanía", como hojas, no son antepasados de ningún otro nodo.
Las estructuras de árbol pueden representar todo tipo de conocimiento taxonómico , como los árboles genealógicos , el árbol evolutivo biológico , el árbol evolutivo de una familia lingüística , la estructura gramatical de una lengua (un ejemplo clave es S → NP VP, lo que significa que una oración es una frase nominal y una frase verbal, cada una de las cuales a su vez tiene otros componentes que tienen otros componentes), la forma en que las páginas web se ordenan lógicamente en un sitio web, árboles matemáticos de conjuntos de números enteros, etcétera.
El Oxford English Dictionary registra el uso de los términos "estructura de árbol" y "diagrama de árbol" desde 1965 en Aspectos de la teoría de la sintaxis de Noam Chomsky . [2]
En una estructura de árbol hay un solo camino desde cualquier punto a cualquier otro punto.
La informática utiliza ampliamente las estructuras de árbol ( véase Árbol (estructura de datos) y telecomunicaciones ).
Para una definición formal, véase teoría de conjuntos , y para una generalización en la que los hijos no son necesariamente sucesores, véase orden de prefijos .


Existen muchas formas de representar visualmente las estructuras de los árboles. Casi siempre, se reducen a variaciones o combinaciones de algunos estilos básicos:
Diagramas de nodos-enlaces clásicos, que conectan nodos entre sí mediante segmentos de línea:
Conjuntos anidados que utilizan el encierro o la contención para mostrar la paternidad; los ejemplos incluyen TreeMaps , mapas fractales y diagramas de Euler :
Diagramas de "carámbanos" en capas que utilizan alineación/adyacencia.
Listas o diagramas que utilizan sangría, a veces llamados " esquemas " o " vistas de árbol ".
Un esquema:
Una vista de árbol:
La correspondencia con los paréntesis anidados fue observada por primera vez por Sir Arthur Cayley :
((arte, artesanía)cultura, ciencia)enciclopedia
o
enciclopedia(cultura(arte, artesanía),ciencia)
Los árboles también se pueden representar radialmente :
La identificación de algunos de los estilos básicos de estructuras de árboles se puede encontrar en: