Centro de rotación instantáneo

Punto fijado a un cuerpo que sufre un movimiento plano.

Bosquejo 1: Centro instantáneo P de un plano en movimiento

El centro instantáneo de rotación (también conocido como centro de velocidad instantánea , ^[1] centro instantáneo o polo de desplazamiento plano ) de un cuerpo que experimenta un movimiento plano es un punto que tiene velocidad cero en un instante particular de tiempo. En este instante, los vectores de velocidad de los demás puntos del cuerpo generan un campo circular alrededor de este centro de rotación idéntico al que se genera en una rotación pura .

El movimiento plano de un cuerpo a menudo se describe utilizando una figura plana que se mueve en un plano bidimensional . El centro instantáneo es el punto en el plano en movimiento alrededor del cual todos los demás puntos giran en un instante de tiempo específico.

El movimiento continuo de un avión tiene un centro instantáneo para cada valor del parámetro tiempo. Esto genera una curva llamada centrodo móvil . Los puntos en el plano fijo correspondientes a estos centros instantáneos forman el centrodo fijo.

La generalización de este concepto al espacio tridimensional es la de girar un tornillo. El tornillo tiene un eje que es una línea en el espacio 3D (no necesariamente que pasa por el origen), el eje de rotación ; el tornillo también tiene un paso finito (una traslación fija a lo largo de su eje correspondiente a una rotación alrededor del eje del tornillo).

Polo de un desplazamiento plano

Boceto 2: Polo de un desplazamiento plano

El centro instantáneo puede considerarse el caso límite del polo de un desplazamiento plano.

El desplazamiento plano de un cuerpo desde la posición 1 a la posición 2 se define por la combinación de una rotación plana y una traslación plana . Para cualquier desplazamiento plano existe un punto en el cuerpo en movimiento que se encuentra en el mismo lugar antes y después del desplazamiento. El desplazamiento puede verse como una rotación alrededor de este polo.

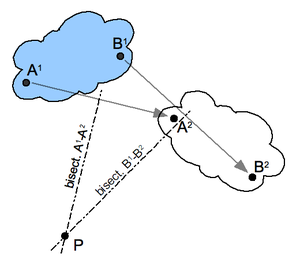
Construcción para el polo de un desplazamiento plano.

Primero, seleccione dos puntos A y B en el cuerpo en movimiento y ubique los puntos correspondientes en las dos posiciones; ver la ilustración. Construya las bisectrices perpendiculares a los dos segmentos A ¹ A ² y B ¹ B ² . La intersección P de estas dos bisectrices es el polo del desplazamiento plano. Observe que A ¹ y A ² se encuentran en un círculo alrededor de P. Esto es cierto para las posiciones correspondientes de cada punto del cuerpo.

Si en un movimiento plano las dos posiciones de un cuerpo están separadas por un instante de tiempo, entonces el polo de un desplazamiento se convierte en el centro instantáneo. En este caso, los segmentos construidos entre las posiciones instantáneas de los puntos A y B se convierten en los vectores de velocidad V _A y V _B . Las líneas perpendiculares a estos vectores de velocidad se cortan en el centro instantáneo.

La construcción algebraica de las coordenadas cartesianas se puede ordenar de la siguiente manera: El punto medio entre y tiene las coordenadas cartesianas ${\displaystyle \left(P_{x},P_{y}\right)}$ ${\displaystyle A^{1}}$ ${\displaystyle A^{2}}$

${\displaystyle A_{x}^{m}={\frac {1}{2}}\left(A_{x}^{1}+A_{x}^{2}\right);\quad A_{y}^{m}={\frac {1}{2}}\left(A_{y}^{1}+A_{y}^{2}\right),}$

y el punto medio entre y tiene las coordenadas cartesianas ${\displaystyle B^{1}}$ ${\displaystyle B^{2}}$

${\displaystyle B_{x}^{m}={\frac {1}{2}}\left(B_{x}^{1}+B_{x}^{2}\right);\quad B_{y}^{m}={\frac {1}{2}}\left(B_{y}^{1}+B_{y}^{2}\right).}$

Los dos ángulos desde hacia y desde hacia medidos en sentido antihorario con respecto a la horizontal están determinados por ${\displaystyle A^{1}}$ ${\displaystyle A^{2}}$ ${\displaystyle B^{1}}$ ${\displaystyle B^{2}}$

${\displaystyle \tan \tau _{A}={\frac {A_{y}^{2}-A_{y}^{1}}{A_{x}^{2}-A_{x}^{1}}},\quad \tan \tau _{B}={\frac {B_{y}^{2}-B_{y}^{1}}{B_{x}^{2}-B_{x}^{1}}}}$

Encuentra la posición de ${\displaystyle P\left(P_{x},P_{y}\right)}$

Método 1:

Tomando las ramas correctas de la tangente . Deje que el centro de la rotación tenga distancias y a los dos puntos medios. Suponiendo una rotación en el sentido de las agujas del reloj (de lo contrario, cambie el signo de ): ${\displaystyle \left(P_{x},P_{y}\right)}$ ${\displaystyle d_{A}}$ ${\displaystyle d_{B}}$ ${\displaystyle \pi /2}$

${\displaystyle {\begin{aligned}P_{x}&=A_{x}^{m}+d_{A}\cos \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{x}^{m}+d_{B}\cos \left(\tau _{B}-{\frac {\pi }{2}}\right);\\P_{y}&=A_{y}^{m}+d_{A}\sin \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{y}^{m}+d_{B}\sin \left(\tau _{B}-{\frac {\pi }{2}}\right).\end{aligned}}}$

Reescribe esto como un sistema no homogéneo de ecuaciones lineales de 4 × 4 con 4 incógnitas (las dos distancias y las dos coordenadas del centro): ${\displaystyle d}$ ${\displaystyle P}$

${\displaystyle {\begin{pmatrix}1&0&-\sin \tau _{A}&0\\1&0&0&-\sin \tau _{B}\\0&1&\cos \tau _{A}&0\\0&1&0&\cos \tau _{B}\end{pmatrix}}{\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\begin{pmatrix}A_{x}^{m}\\B_{x}^{m}\\A_{y}^{m}\\B_{y}^{m}\end{pmatrix}}.}$

Las coordenadas del centro de rotación son los dos primeros componentes del vector solución.

${\displaystyle {\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\frac {1}{\sin \left(\tau _{A}-\tau _{B}\right)}}{\begin{pmatrix}\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\sin \tau _{B}+B_{x}^{m}\sin \tau _{A}\cos \tau _{B}-A_{x}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(A_{x}^{m}-B_{x}^{m}\right)\cos \tau _{A}\cos \tau _{B}+A_{y}^{m}\sin \tau _{A}\cos \tau _{B}-B_{y}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{B}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{A}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\\\end{pmatrix}}.}$

Método 2:

Encuentre las ecuaciones de las bisectrices de dos segmentos A ¹ A ² y B ¹ B ² de la siguiente manera

La ecuación de una recta en forma punto-pendiente es: donde está el punto y es la pendiente. ${\displaystyle y-y_{0}=m(x-x_{0})}$ ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle m}$

La ecuación de la bisectriz de A ¹ A ² es ${\displaystyle y-A_{y}^{m}=\tan \tau _{A}\left(x-A_{x}^{m}\right)}$

La ecuación de la bisectriz de B ¹ B ² es ${\displaystyle y-B_{y}^{m}=\tan \tau _{B}\left(x-B_{x}^{m}\right)}$

Estas dos bisectrices se cortan por lo que se puede escribir un sistema de 2 ecuaciones con 2 incógnitas y coeficientes. ${\displaystyle P\left(P_{x},P_{y}\right)}$

${\displaystyle {\begin{cases}P_{y}-A_{y}^{m}=\tan \tau _{A}\left(P_{x}-A_{x}^{m}\right)\\P_{y}-B_{y}^{m}=\tan \tau _{B}\left(P_{x}-B_{x}^{m}\right)\end{cases}}}$

La solución de este sistema es

${\displaystyle P_{x}={\frac {B_{y}^{m}-A_{y}^{m}+A_{x}^{m}\tan \tau _{A}-B_{x}^{m}\tan \tau _{B}}{\tan \tau _{A}-\tan \tau _{B}}},\qquad P_{y}={\frac {B_{y}^{m}-A_{y}^{m}+\tan \tau _{A}\left(A_{x}^{m}-B_{x}^{m}\right)}{\tan \tau _{A}-\tan \tau _{B}}}+B_{y}^{m}}$

Traducción pura

Si el desplazamiento entre dos posiciones es una traslación pura, entonces las bisectrices perpendiculares de los segmentos A ¹ B ¹ y A ² B ² forman rectas paralelas. Se considera que estas líneas se cruzan en un punto de la línea en el infinito , por lo que se dice que el polo de este desplazamiento plano "está en el infinito" en la dirección de las bisectrices perpendiculares.

En el límite, la traslación pura se convierte en movimiento plano con vectores de velocidad puntuales paralelos. En este caso, se dice que el centro instantáneo está en el infinito en la dirección perpendicular a los vectores de velocidad.

Centro instantáneo de una rueda que rueda sin deslizarse

Boceto 3: Rueda rodante.

Centro instantáneo de rotación de una rueda rodante descompuesto en puntos. Descomponiendo la rueda rodante en varios puntos, se puede ver más fácilmente cómo todos los puntos de la rueda giran alrededor de un único punto en cada instante. Este punto es el centro instantáneo de rotación, que se muestra en negro.

Considere el movimiento plano de una rueda circular que rueda sin deslizarse en una carretera lineal; ver dibujo 3. La rueda gira alrededor de su eje M, que se traslada en una dirección paralela a la carretera. El punto de contacto P de la rueda con la carretera no resbala, lo que significa que el punto P tiene velocidad cero con respecto a la carretera. Así, en el instante en que el punto P de la rueda entra en contacto con la carretera, se convierte instantáneamente en un centro.

El conjunto de puntos de la rueda en movimiento que se convierten en centros instantáneos es el círculo mismo, que define el centrodo en movimiento. Los puntos en el plano fijo que corresponden a estos centros instantáneos es la línea de la carretera, que define el centrodo fijo.

El vector velocidad de un punto A en la rueda es perpendicular al segmento AP y es proporcional a la longitud de este segmento. En particular, las velocidades de los puntos de la rueda están determinadas por la velocidad angular de la rueda en rotación alrededor de P. Los vectores de velocidad de varios puntos se ilustran en el esquema 3 y se pueden calcular utilizando la siguiente ecuación:

${\displaystyle {\vec {v}}={\vec {\omega }}\times {\vec {r}}_{A}}$

donde es la velocidad del punto A, la velocidad angular de la rueda y el vector del punto P a A. ${\displaystyle {\vec {v}}}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {r}}_{A}}$

Cuanto más lejos esté un punto de la rueda del centro instantáneo P, proporcionalmente mayor será su velocidad. Por lo tanto, el punto en la parte superior de la rueda se mueve en la misma dirección que el centro M de la rueda, pero dos veces más rápido, ya que está a dos veces la distancia de P. Todos los puntos que están a una distancia igual al radio de la rueda La rueda 'r' del punto P se mueve a la misma velocidad que el punto M pero en diferentes direcciones. Esto se muestra para un punto de la rueda que tiene la misma rapidez que M pero se mueve en la dirección tangente al círculo alrededor de P.

Centro de rotación relativo para dos cuerpos planos en contacto

Bosquejo 4: Ejemplo de centro relativo de rotación. Dos cuerpos en contacto en C , uno que gira alrededor de A y el otro alrededor de B , deben tener un centro de rotación relativo en algún lugar a lo largo de la línea AB . Dado que las piezas no pueden interpenetrar , el centro de rotación relativo también debe estar a lo largo de la dirección normal al contacto y a través de C. La única solución posible es si el centro relativo está en D .

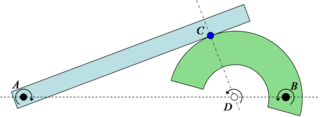
Si dos cuerpos rígidos planos están en contacto y cada cuerpo tiene su propio centro de rotación distinto, entonces el centro de rotación relativo entre los cuerpos tiene que estar en algún lugar de la línea que conecta los dos centros. Como resultado, dado que la rodadura pura sólo puede existir cuando el centro de rotación está en el punto de contacto (como se ve arriba con la rueda en la carretera), sólo lo es cuando el punto de contacto pasa por la línea que conecta los dos centros de rotación. que se puede lograr una rodadura pura. Esto se conoce en el diseño de engranajes involutivos como punto de paso, donde no hay deslizamiento relativo entre los engranajes. De hecho, la relación de transmisión entre las dos partes giratorias se encuentra mediante la relación de las dos distancias al centro relativo. En el ejemplo del Bosquejo 4, la relación de apalancamiento es ${\displaystyle \gamma ={\frac {AD}{BD}}}$

Centro instantáneo de rotación y mecanismos.

El boceto 1 anterior muestra un varillaje de cuatro barras donde se ilustran varios centros instantáneos de rotación. El cuerpo rígido señalado con las letras BAC está conectado con enlaces P ₁ -A y P ₂ -B a una base o marco.

Las tres partes móviles de este mecanismo (la base no se mueve) son: enlace P ₁ -A, enlace P ₂ -B y cuerpo BAC. Para cada una de estas tres partes se puede determinar un centro de rotación instantáneo.

Considerando el primer eslabón P ₁ -A: todos los puntos de este eslabón, incluido el punto A, giran alrededor del punto P ₁ . Dado que P ₁ es el único punto que no se mueve en el plano dado, se le puede llamar centro instantáneo de rotación de este eslabón. El punto A, a la distancia P ₁ -A de P ₁ , se mueve con un movimiento circular en una dirección perpendicular al enlace P ₁ -A, como lo indica el vector V _A .

Lo mismo se aplica al eslabón P ₂ -B: el punto P ₂ es el centro instantáneo de rotación de este eslabón y el punto B se mueve en la dirección indicada por el vector V _B .

Para determinar el centro instantáneo de rotación del tercer elemento del varillaje, el cuerpo BAC, se utilizan los dos puntos A y B porque se conocen sus características de movimiento, derivadas de la información sobre los eslabones P ₁ -A y P ₂ -. B.

La dirección de la velocidad del punto A está indicada por el vector V _A . Su centro instantáneo de rotación debe ser perpendicular a este vector (ya que V _A está ubicado tangencialmente en la circunferencia de un círculo). La única línea que cumple el requisito es una línea colineal con el enlace P ₁ -A. En algún lugar de esta línea hay un punto P, el centro instantáneo de rotación del cuerpo BAC.

Lo que se aplica al punto A también se aplica al punto B, por lo tanto este centro instantáneo de rotación P se ubica en una recta perpendicular al vector V _B , una recta colineal con el enlace P ₂ -B. Por lo tanto, el centro instantáneo de rotación P del cuerpo BAC es el punto donde se cruzan las líneas que pasan por P ₁ -A y P ₂ -B.

Dado que este centro instantáneo de rotación P es el centro de todos los puntos del cuerpo BAC para cualquier punto aleatorio, digamos el punto C, se pueden determinar la velocidad y la dirección del movimiento: conecte P con C. La dirección del movimiento del punto C es perpendicular a esta conexión. La velocidad es proporcional a la distancia al punto P.

Continuando con este enfoque con los dos eslabones P ₁ -A y P ₂ -B girando alrededor de sus propios centros instantáneos de rotación, se puede determinar el centrodo para el centro instantáneo de rotación P. A partir de esto se puede determinar la trayectoria de movimiento de C o de cualquier otro punto del cuerpo BAC.

Ejemplos de aplicación

En la investigación biomecánica se observa el centro instantáneo de rotación para el funcionamiento de las articulaciones de las extremidades superiores e inferiores. ^[2] Por ejemplo, en el análisis de las articulaciones de la rodilla , ^{[3] [4] [5]} del tobillo , ^[6] o del hombro . ^{[7] [8]} Este conocimiento ayuda a desarrollar articulaciones y prótesis artificiales , como las del codo ^[9] o las de los dedos. ^[10]

Estudio de las articulaciones de los caballos: "...los vectores de velocidad determinados a partir de los centros instantáneos de rotación indicaron que las superficies de las articulaciones se deslizan unas sobre otras". ^[11]

Estudios sobre el giro de una embarcación que se desplaza por el agua. ^[12]

Las características de frenado de un automóvil pueden mejorarse variando el diseño del mecanismo del pedal de freno. ^[13]

Diseñar la suspensión de una bicicleta, ^[14] o de un coche. ^[15]

En el caso del eslabón acoplador en un varillaje de cuatro barras , como una suspensión de doble horquilla en vista frontal, las perpendiculares a la velocidad se encuentran a lo largo de los eslabones que unen el eslabón puesto a tierra con el eslabón acoplador. Esta construcción se utiliza para establecer el centro de balanceo cinemático de la suspensión.

Ver también

• Velocidad angular
• La teoría de Burmester.
• Centrode
• Grupo de reflexión puntual.
• Cuerpo rígido
• Centro de rollo
• Rotación alrededor de un eje fijo.
• Eje de tornillo
• Rotación bidimensional

Referencias

1. Diccionario ilustrado de ingeniería mecánica: inglés, alemán, francés, holandés, ruso (Springer Science & Business Media, 17 de abril de 2013 - 422 páginas)
2. "Fisiología muscular: brazo de momento articular".
3. Descripción y medición del movimiento de la articulación de la rodilla ^{[ enlace muerto permanente ]}
4. Moorehead JD, Montgomery SC, Harvey DM (septiembre de 2003). "Estimación instantánea del centro de rotación mediante la técnica de Reuleaux y una técnica de extrapolación lateral". J Biomecánica . 36 (9): 1301–7. doi :10.1016/S0021-9290(03)00156-8. PMID  12893038.
5. Hollman JH, Deusinger RH, Van Dillen LR, Matava MJ (agosto de 2003). "Diferencias de género en la cinemática de deslizamiento y rodadura de la superficie de la rodilla". Clin Orthop Relat Res . 413 (413): 208–21. doi :10.1097/01.blo.0000072902.36018.fe. PMID  12897612. S2CID  45191914.
6. Maganaris CN, Baltzopoulos V, Sargeant AJ (agosto de 1998). "Cambios en el momento del brazo del tendón de Aquiles desde el reposo hasta la flexión plantar isométrica máxima: observaciones in vivo en el hombre". Revista de fisiología . 510 (parte 3): 977–85. doi :10.1111/j.1469-7793.1998.977bj.x. PMC 2231068 . PMID  9660906. Archivado desde el original el 8 de septiembre de 2012. 
7. Biomecánica del hombro
8. Poppen NK, Walker PS (marzo de 1976). "Movimiento normal y anormal del hombro". J Cirugía de la articulación ósea Am . 58 (2): 195-201. doi :10.2106/00004623-197658020-00006. PMID  1254624.
9. US 5030237  Prótesis de codo
10. "Implante de articulación del dedo de pirocarbono" (PDF) . Archivado desde el original (PDF) el 21 de julio de 2011 . Consultado el 22 de agosto de 2008 .
11. Colahan P, Piotrowski G, Poulos P (septiembre de 1988). "Análisis cinemático de los centros instantáneos de rotación de la articulación metacarpofalángica equina". Soy J Vet Res . 49 (9): 1560–5. PMID  3223666.
12. "PARTE VI Navegación y maniobras de embarcaciones" (PDF) . Archivado desde el original (PDF) el 15 de diciembre de 2009 . Consultado el 22 de agosto de 2008 .
13. GB 1443270 Soportes de pedal de freno de relación mecánica variable - General Motors, 1976 
14. US 7100930 Sistema de suspensión trasera de bicicleta 
15. Reza N. Jazar (2008). Dinámica de vehículos: teoría y aplicación. Berlín: Springer. ISBN 978-0-387-74243-4.