Sprouts es un juego imparcial de lápiz y papel que puede analizarse por sus propiedades matemáticas . Fue inventado por los matemáticos John Horton Conway y Michael S. Paterson [1] en la Universidad de Cambridge a principios de los años 1960. La configuración es incluso más sencilla que la del popular juego Dots and Boxes , pero la jugabilidad se desarrolla de forma mucho más artística y orgánica.
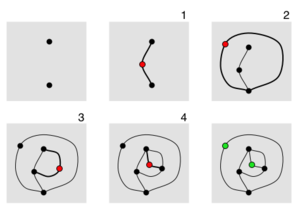
El juego lo juegan dos jugadores, [2] comenzando con algunos puntos dibujados en una hoja de papel. Los jugadores se turnan, donde cada turno consiste en trazar una línea entre dos puntos (o desde un punto hacia sí mismo) y agregar un nuevo punto en algún lugar a lo largo de la línea. Los jugadores están limitados por las siguientes reglas:
En el llamado juego normal , gana el jugador que realiza el último movimiento. En el juego misère , pierde el jugador que realiza el último movimiento. Misère Sprouts es quizás el único juego combinatorio de misère que se juega de forma competitiva en un foro organizado. [3]
El diagrama de la derecha muestra un juego de 2 puntos de Sprouts de juego normal. Después del cuarto movimiento, la mayoría de los puntos están muertos : tienen tres líneas adjuntas, por lo que no pueden usarse como puntos finales para una nueva línea. Hay dos puntos (que se muestran en verde) que todavía están vivos y tienen menos de tres líneas unidas. Sin embargo, es imposible hacer otro movimiento, porque una línea desde un punto vivo hacia sí misma crearía cuatro conexiones, y una línea desde un punto vivo al otro cruzaría líneas. Por lo tanto, no es posible un quinto movimiento y el primer jugador pierde. Los puntos vivos al final del juego se llaman supervivientes y juegan un papel clave en el análisis de Sprouts.
El juego de Sprouts siempre termina, aunque este hecho no se desprende de las reglas del juego, ya que el número de casillas aumenta con cada jugada. La forma de entender por qué el juego siempre termina es considerar el número de vidas (oportunidades de conectar una línea) en lugar del número de puntos. Entonces, se puede demostrar que si el juego comienza con n puntos, terminará en no más de 3 n − 1 movimientos y no menos de 2 n movimientos.
En las siguientes pruebas , se supone que un juego comienza con n puntos y dura exactamente m movimientos.
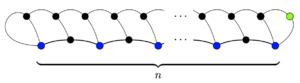
Cada lugar comienza con tres vidas y cada movimiento reduce en uno el número total de vidas en el juego (se pierden dos vidas al final de la línea, pero el nuevo lugar tiene una vida). Entonces, al final del juego quedan 3 n − m vidas. Cada punto superviviente tiene sólo una vida (de lo contrario, habría otro movimiento que uniría ese punto a sí mismo), por lo que hay exactamente 3 n − m supervivientes. Debe haber al menos un superviviente, es decir, el lugar añadido en el movimiento final. Entonces 3 norte − metro ≥ 1 ; por tanto, un juego no puede durar más de 3 n − 1 movimientos.
Este límite superior es en realidad el máximo y se puede alcanzar de muchas maneras asegurándose de que solo haya un superviviente al final del juego. Por ejemplo, el juego de la derecha tiene un superviviente y 3 n − 1 movimientos.
Al final del juego, un punto muerto se denomina vecino de un superviviente si está adyacente a ese superviviente o, si el superviviente tiene un bucle, está adyacente a un punto adyacente al superviviente. Esto se ilustra en el diagrama de la derecha. Cada superviviente tiene exactamente dos vecinos muertos. Ningún punto muerto puede ser vecino de dos supervivientes diferentes, porque de lo contrario se produciría un movimiento que uniría a los supervivientes. Todos los demás puntos muertos (que no son vecinos de un superviviente) se llaman fariseos (del hebreo " separados "). Supongamos que hay fariseos . Entonces
desde puntos iniciales + movimientos = puntos totales al final del juego = supervivientes + vecinos + fariseos. Reorganizar da:
En consecuencia, una partida dura al menos 2 n jugadas y el número de fariseos es divisible por 4.
Este límite inferior de la duración de un juego es en realidad el mínimo. El diagrama de la derecha muestra un juego completo de 2 n movimientos. Tiene n supervivientes, 2 n vecinos y 0 fariseos.
Los juegos reales parecen convertirse en una batalla sobre si el número de movimientos será k o k + 1, siendo bastante improbables otras posibilidades. [4] Un jugador intenta crear regiones cerradas que contengan supervivientes (reduciendo así el número total de movimientos que se jugarán) y el otro intenta crear fariseos (aumentando así el número de movimientos que se jugarán).
Dado que Sprouts es un juego finito en el que no es posible empatar, existe una estrategia perfecta para el primer o el segundo jugador, dependiendo del número de puntos iniciales. La cuestión principal sobre una determinada posición inicial es determinar qué jugador puede forzar una victoria si juega perfectamente.
Cuando la estrategia ganadora es para el primer jugador, se dice que el resultado de la posición es una "victoria", y cuando la estrategia ganadora es para el segundo jugador, se dice que el resultado de la posición es una "pérdida". (porque es una pérdida desde el punto de vista del primer jugador).
El resultado se determina desarrollando el árbol de juego de la posición inicial. Esto se puede hacer a mano sólo para un pequeño número de lugares, y todos los resultados nuevos desde 1990 se han obtenido mediante búsquedas exhaustivas con computadoras.
Winning Ways for your Mathematical Plays informa que Denis Mollison demostró que el juego normal de 6 puntos era una victoria para el segundo jugador, con un análisis hecho a mano de 47 páginas. Se mantuvo como récord durante mucho tiempo, hasta el primer análisis por ordenador, realizado en la Universidad Carnegie Mellon en 1990 por David Applegate , Guy Jacobson y Daniel Sleator . [5] Alcanzaron hasta 11 puestos con algunos de los mejores hardware disponibles en ese momento.
Applegate, Jacobson y Sleator observaron un patrón en sus resultados y conjeturaron que el primer jugador tiene una estrategia ganadora cuando el número de puestos dividido por seis deja un resto de tres, cuatro o cinco. Esta es una forma matemática de decir que el patrón que muestra el resultado de la siguiente tabla se repite indefinidamente, con un período de seis puntos.
En 2001, Riccardo Focardi y Flamina Luccio describieron un método para demostrar manualmente que el juego normal de 7 puntos es una pérdida. [6]
Luego, los resultados del cálculo fueron ampliados en 2006 por Josh Jordan hasta 14 puntos. En 2007, Julien Lemoine y Simon Viennot introdujeron un algoritmo basado en el concepto de números para acelerar el cálculo, alcanzando hasta 32 puntos. [7] Han ampliado el cómputo hasta 44 puestos en 2011, y tres posiciones de salida aisladas, con 46, 47 y 53 puestos. [8]
Los resultados del juego normal hasta el momento son todos consistentes con la conjetura de Applegate, Jacobson y Sleator.
El historial de cálculo de la versión misère de Sprouts es muy similar al de la versión normal, con las mismas personas involucradas. Sin embargo, la versión misère es más difícil de calcular y el progreso ha sido significativamente más lento.
En 1990, Applegate, Jacobson y Sleator alcanzaron hasta nueve puestos. Con base en sus resultados, conjeturaron que el resultado sigue un patrón regular del período cinco. Sin embargo, esta conjetura quedó invalidada en 2007 cuando Josh Jordan y Roman Khorkov ampliaron el análisis de misère hasta 12 puntos: el juego de misère de 12 puntos es una victoria, y no la pérdida conjeturada. El mismo equipo alcanzó hasta 16 puestos en 2009. [9] El mismo año, Julien Lemoine y Simon Viennot alcanzaron 17 puestos con algoritmos complicados. [10] Pudieron ampliar su análisis hasta 20 puntos en 2011. [8]
Ahora se conjetura que los resultados del juego misère siguen un patrón de longitud seis con algunos valores excepcionales: el primer jugador gana en misère Sprouts cuando el resto ( mod 6) es cero, cuatro o cinco, excepto que el primer jugador gana el uno. -juego de puntos y pierde el juego de cuatro puntos. La siguiente tabla muestra el patrón, con los dos valores irregulares en negrita.
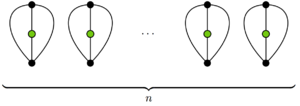
Una variante del juego, llamada coles de Bruselas por la verdura crucífera , comienza con varias cruces, es decir, puntos con cuatro extremos libres. Cada movimiento implica unir dos extremos libres con una curva, nuevamente sin cruzar ninguna línea existente y luego realizar un trazo corto a través de la línea para crear dos nuevos extremos libres. Este juego es finito y el número total de movimientos (y por tanto el ganador del juego) está predeterminado por el número inicial de cruces: los jugadores no pueden afectar el resultado con su juego. Por lo tanto, esta variante puede denominarse, después de la categorización de las matemáticas de Conway, un "juego de un solo jugador".
Cada movimiento elimina dos extremos libres e introduce dos más. Sin embargo, el juego está destinado a terminar cuando algunos extremos libres quedan aislados. Con n cruces iniciales, el número de movimientos, sorprendentemente, siempre será 5 n − 2. En consecuencia, un juego que comience con un número impar de cruces será la primera victoria del jugador, mientras que un juego que comience con un número par será una segunda victoria. El jugador gana independientemente de los movimientos.
Para probar esto, primero argumentamos que el juego debe terminar. Luego, calcularemos con precisión cuántos movimientos necesita para finalizar. El resultado del juego queda entonces implícito, como ya se ha descrito.
Trate cada cruz como un gráfico con 5 vértices y 4 aristas. En la posición inicial con n cruces, tenemos un gráfico plano con v = 5 n vértices, e = 4 n aristas, f = 1 cara y k = n componentes conectados . La característica de Euler para gráficos planos conectados es 2. En un gráfico plano desconectado , obtenemos
Después de m movimientos, tenemos:
Entonces por lo anterior, tenemos
A continuación, tenga en cuenta que cada vez que agregamos una cruz, nos aseguramos de que cada lado de esta cruz termine con un vértice de grado 1. Así, a lo largo del juego, cada cara tiene al menos un vértice de grado 1. Sin embargo, el número de vértices de grado 1 es invariante durante todo el juego y permanece en 4 n . Por tanto, f es como máximo 4 n .
De esto, vemos que m = f − k − 1 + n es como máximo 5 n − 2 (ya que k es al menos 1 y f es como máximo 4 n ). Por lo tanto, el juego debe terminar, y debe terminar en un máximo de 5 n − 2 movimientos. Ahora argumentamos que debe terminar en exactamente 5 n − 2 movimientos.
En la configuración final ninguna cara puede tener más de un vértice de grado 1, ya que de lo contrario podríamos conectarlos con una cruz y aún así habría movimiento legal. Cada cara tiene al menos uno de esos vértices, por lo que debe terminar exactamente con uno de esos vértices. Entonces, en la configuración final, f es exactamente 4 n .
De manera similar, en la configuración final, el gráfico debe estar conectado, ya que la cara exterior tiene al menos un vértice de grado 1 por componente conectado y no puede tener más de uno de esos vértices. Entonces, en la configuración final, k es exactamente 1.
Así, para obtener la configuración final, debemos haber tenido m = f − k −1+ n = 4 n −1−1+ n = 5 n −2.
También se puede jugar una combinación de coles estándar y coles de Bruselas. El juego comienza con un número arbitrario ( n ) de puntos o cruces. En cada turno, el jugador elige agregar un punto o una cruz a lo largo de la línea que acaba de dibujar. La duración del juego está comprendida entre (2 n ) y ( 5 n − 2 ), dependiendo del número de puntos o cruces que se hayan añadido.
Para n = 1, comenzando con un punto, el juego terminará después de 2 movimientos. Comenzando con una cruz, terminará después de 2 movimientos si el primer jugador agrega un punto, después de 3 movimientos si agrega una cruz: por lo tanto, el primer jugador tiene una estrategia ganadora tanto para la versión normal como para la misère. Para n > 1, el análisis no se completa.
{{cite web}}: Falta o está vacío |url=( ayuda )Bibliografía