Conducción balística

Movimiento de portadores de carga con dispersión despreciable

En física mesoscópica , la conducción balística ( transporte balístico ) es el flujo (o transporte ) sin impedimentos de portadores de carga (generalmente electrones ), o partículas portadoras de energía, a lo largo de distancias relativamente largas en un material. En general, la resistividad de un material existe porque un electrón, mientras se mueve dentro de un medio, se dispersa por impurezas, defectos , fluctuaciones térmicas de iones en un sólido cristalino o, en general, por cualquier átomo/molécula que se mueva libremente y que componga un gas o líquido. Sin dispersión, los electrones simplemente obedecen la segunda ley de movimiento de Newton a velocidades no relativistas .

El camino libre medio de una partícula puede describirse como la longitud promedio que la partícula puede viajar libremente, es decir, antes de una colisión, que podría cambiar su momento. El camino libre medio puede aumentarse reduciendo el número de impurezas en un cristal o bajando su temperatura. El transporte balístico se observa cuando el camino libre medio de la partícula es (mucho) más largo que la dimensión del medio a través del cual viaja la partícula. La partícula altera su movimiento solo al chocar con las paredes . En el caso de un cable suspendido en el aire/vacío, la superficie del cable desempeña el papel de la caja que refleja los electrones y evita que salgan hacia el espacio vacío/aire libre. Esto se debe a que hay una energía que se debe pagar para extraer el electrón del medio ( función de trabajo ).

La conducción balística se observa típicamente en estructuras cuasi-1D, como nanotubos de carbono o nanocables de silicio , debido a los efectos de cuantificación de tamaño extremos en estos materiales. La conducción balística no se limita a los electrones (o huecos), sino que también puede aplicarse a los fonones . Teóricamente, es posible que la conducción balística se extienda a otras cuasipartículas, pero esto no se ha verificado experimentalmente. Para un ejemplo específico, el transporte balístico se puede observar en un nanocable de metal : debido al pequeño tamaño del cable ( escala nanométrica o escala de 10 ⁻⁹ metros) y al camino libre medio que puede ser más largo que el de un metal. ^[1]

La conducción balística se diferencia de la superconductividad debido a 1) una resistencia finita y distinta de cero y 2) la ausencia del efecto Meissner en el material. La presencia de resistencia implica que el calor se disipa en los conductores fuera del conductor "balístico", donde pueden producirse efectos de dispersión inelástica.

Teoría

Mecanismos de dispersión

En general, los portadores exhibirán conducción balística cuando donde es la longitud de la parte activa del dispositivo (por ejemplo, un canal en un MOSFET ). es el camino libre medio para el portador que puede darse mediante la regla de Matthiessen , escrita aquí para electrones: ${\displaystyle L\leq \lambda _{\rm {MFP}}}$ ${\displaystyle L}$ ${\displaystyle \lambda _{\rm {MFP}}}$

${\displaystyle {\frac {1}{\lambda _{\mathrm {MFP} }}}={\frac {1}{\lambda _{\mathrm {el-el} }}}+{\frac {1}{\lambda _{\mathrm {ap} }}}+{\frac {1}{\lambda _{\mathrm {op,ems} }}}+{\frac {1}{\lambda _{\mathrm {op,abs} }}}+{\frac {1}{\lambda _{\mathrm {impurity} }}}+{\frac {1}{\lambda _{\mathrm {defect} }}}+{\frac {1}{\lambda _{\mathrm {boundary} }}}}$

dónde

• ${\displaystyle \lambda _{\mathrm {el-el} }}$es la longitud de dispersión electrón-electrón,
• ${\displaystyle \lambda _{\mathrm {ap} }}$es la longitud de dispersión del fonón acústico (emisión y absorción),
• ${\displaystyle \lambda _{\mathrm {op,ems} }}$es la longitud de dispersión de emisión de fonones ópticos,
• ${\displaystyle \lambda _{\mathrm {op,abs} }}$es la longitud de dispersión de absorción de fonones ópticos,
• ${\displaystyle \lambda _{\mathrm {impurity} }}$es la longitud de dispersión de impurezas electrónicas,
• ${\displaystyle \lambda _{\mathrm {defect} }}$es la longitud de dispersión del defecto electrónico,
• y es la longitud de dispersión de electrones con el límite. ${\displaystyle \lambda _{\mathrm {boundary} }}$

En términos de mecanismos de dispersión, la emisión óptica de fonones normalmente domina, dependiendo del material y las condiciones de transporte. También hay otros mecanismos de dispersión que se aplican a diferentes portadores que no se consideran aquí (por ejemplo, dispersión de fonones en interfaz remota, dispersión de Umklapp ). Para obtener estas tasas de dispersión características, sería necesario derivar un hamiltoniano y resolver la regla de oro de Fermi para el sistema en cuestión.

Un transistor de efecto de campo de nanocintas de grafeno (GNR-FET). Aquí los contactos A y B están en dos niveles de Fermi diferentes y . ${\displaystyle E_{\rm {F_{A}}}}$ ${\displaystyle E_{\rm {F_{B}}}}$

Formalismo de Landauer-Büttiker

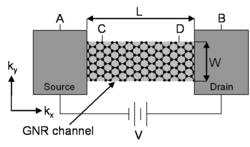
En 1957, Rolf Landauer propuso que la conducción en un sistema unidimensional podría considerarse un problema de transmisión. Para el transistor de efecto de campo de nanocinta de grafeno unidimensional (GNR-FET) de la derecha (donde se supone que el canal es balístico), la corriente de A a B, dada por la ecuación de transporte de Boltzmann , es

${\displaystyle I_{\rm {AB}}={\frac {g_{\text{s}}e}{h}}\int _{E_{\rm {F_{B}}}}^{E_{\rm {F_{A}}}}M(E)f^{\prime }(E)T(E)dE}$,

donde g _s = 2, debido a la degeneración de espín , e es la carga del electrón, h es la constante de Planck y son los niveles de Fermi de A y B , M ( E ) es el número de modos de propagación en el canal, f ′( E ) es la desviación de la distribución de electrones de equilibrio (perturbación), y T(E) es la probabilidad de transmisión ( T = 1 para balística). ^{[ cita requerida ]} Basado en la definición de conductancia ${\displaystyle E_{\rm {F_{A}}}}$ ${\displaystyle E_{\rm {F_{B}}}}$

${\displaystyle G={\frac {I}{V}}}$,

y la separación de voltaje entre los niveles de Fermi es aproximadamente , se deduce que ${\displaystyle eV=E_{\rm {F_{A}}}-E_{\rm {F_{B}}}}$

${\displaystyle G=G_{0}MT}$, con ${\displaystyle G_{0}={\frac {2e^{2}}{h}}}$

donde M es el número de modos en el canal de transmisión y se incluye el espín. se conoce como la conductancia cuántica . Los contactos tienen una multiplicidad de modos debido a su mayor tamaño en comparación con el canal. Por el contrario, el confinamiento cuántico en el canal GNR 1D restringe el número de modos debido a la degeneración de portadores y las restricciones de la relación de dispersión de energía y la zona de Brillouin . Por ejemplo, los electrones en los nanotubos de carbono tienen dos modos intervalley y dos modos de espín. Dado que los contactos y el canal GNR están conectados por conductores, la probabilidad de transmisión es menor en los contactos A y B. ${\displaystyle G_{0}}$

${\displaystyle T\approx {\frac {M}{M_{\rm {contact}}}}}$.

Por lo tanto, la conductancia cuántica es aproximadamente la misma si se mide en A y B o en C y D.

El formalismo de Landauer-Büttiker se cumple siempre que los portadores sean coherentes (lo que significa que la longitud del canal activo es menor que el camino libre medio de ruptura de fase) y las funciones de transmisión se pueden calcular a partir de la ecuación de Schrödinger o aproximarse mediante aproximaciones semiclásicas , como la aproximación WKB . Por lo tanto, incluso en el caso de un transporte balístico perfecto, existe una conductancia balística fundamental que satura la corriente del dispositivo con una resistencia de aproximadamente 12,9 kΩ por modo (degeneración de espín incluida). ^[2] Sin embargo, existe una generalización del formalismo de transporte de Landauer-Büttiker aplicable a problemas dependientes del tiempo en presencia de disipación . ^{[3] [4]}

Importancia

La conducción balística permite el uso de las propiedades mecánicas cuánticas de las funciones de onda de los electrones . El transporte balístico es coherente en términos de mecánica ondulatoria . Fenómenos como la interferencia de doble rendija , la resonancia espacial (y otros efectos ópticos o similares a las microondas ) podrían explotarse en sistemas electrónicos a escala nanométrica en sistemas que incluyen nanocables y nanotubos .

El fenómeno ampliamente conocido de la resistencia de contacto eléctrico o ECR, surge cuando una corriente eléctrica que fluye a través de una interfaz rugosa se restringe a un número limitado de puntos de contacto. El tamaño y la distribución de estos puntos de contacto están regidos por las estructuras topológicas de las superficies de contacto que forman el contacto eléctrico. En particular, para superficies con una dimensión fractal alta , los puntos de contacto pueden ser muy pequeños. En tales casos, cuando el radio del punto de contacto es menor que el camino libre medio de los electrones , la resistencia está dominada por el mecanismo de Sharvin, en el que los electrones viajan balísticamente a través de estos microcontactos con una resistencia que puede describirse mediante lo siguiente ^[5] ${\displaystyle \lambda }$

${\displaystyle R_{\rm {S}}={\frac {\lambda (\rho _{1}+\rho _{2})}{2a}}.}$

Este término, donde y corresponden a la resistividad específica de las dos superficies en contacto, se conoce como resistencia de Sharvin. Los contactos eléctricos que dan lugar a la conducción balística de electrones se conocen como contactos de Sharvin . Cuando el radio de un punto de contacto es mayor que el camino libre medio de los electrones, la resistencia de contacto se puede tratar de forma clásica. ${\displaystyle \rho _{1}}$ ${\displaystyle \rho _{2}}$

Analogías ópticas

Una comparación con la luz proporciona una analogía entre la conducción balística y no balística. Los electrones balísticos se comportan como la luz en una guía de ondas o en un conjunto óptico de alta calidad. Los electrones no balísticos se comportan como la luz difundida en la leche o reflejada en una pared blanca o en un trozo de papel.

Los electrones pueden dispersarse de varias formas en un conductor. Los electrones tienen varias propiedades: longitud de onda (energía), dirección, fase y orientación del espín. Los distintos materiales tienen distintas probabilidades de dispersión, lo que provoca distintas tasas de incoherencia (estocasticidad). Algunos tipos de dispersión solo pueden provocar un cambio en la dirección de los electrones, mientras que otros pueden provocar una pérdida de energía.

Consideremos una fuente coherente de electrones conectada a un conductor. A lo largo de una distancia limitada, la función de onda del electrón seguirá siendo coherente. Aún se puede predecir de manera determinista su comportamiento (y utilizarlo para realizar cálculos teóricos). Después de una distancia mayor, la dispersión hace que cada electrón tenga una fase y/o dirección ligeramente diferente. Pero sigue sin haber casi ninguna pérdida de energía. Como la luz monocromática que pasa a través de la leche, los electrones experimentan interacciones elásticas . La información sobre el estado de los electrones en la entrada se pierde entonces. El transporte se vuelve estadístico y estocástico . Desde el punto de vista de la resistencia, el movimiento estocástico (no orientado) de los electrones es inútil incluso si llevan la misma energía: se mueven térmicamente. Si los electrones también experimentan interacciones inelásticas , pierden energía y el resultado es un segundo mecanismo de resistencia. Los electrones que experimentan una interacción inelástica son entonces similares a la luz no monocromática.

Para el correcto uso de esta analogía es necesario tener en cuenta varios hechos:

1. Los fotones son bosones y los electrones son fermiones ;
2. Existe repulsión coulombiana entre electrones, por lo que esta analogía es buena sólo para la conducción de un solo electrón porque los procesos electrónicos son fuertemente no lineales y dependen de otros electrones;
3. Es más probable que un electrón pierda más energía que un fotón, debido a que la masa en reposo del electrón no es cero ;
4. Las interacciones de los electrones con el entorno, entre ellos y con otras partículas son generalmente más fuertes que las interacciones con y entre fotones.

Ejemplos

Como ya se ha mencionado, las nanoestructuras como los nanotubos de carbono o las nanocintas de grafeno suelen considerarse balísticas, pero estos dispositivos solo se parecen mucho a la conducción balística. Su balisticidad es de casi 0,9 a temperatura ambiente. ^[6]

Nanotubos de carbono y nanocintas de grafeno

El mecanismo de dispersión dominante a temperatura ambiente es el de los electrones que emiten fonones ópticos. Si los electrones no se dispersan con suficientes fonones (por ejemplo, si la tasa de dispersión es baja), el camino libre medio tiende a ser muy largo ( m). Por lo tanto, un nanotubo o una nanocinta de grafeno podría ser un buen conductor balístico si los electrones en tránsito no se dispersan con demasiados fonones y si el dispositivo tiene una longitud de unos 100 nm. Se ha descubierto que este régimen de transporte depende de la estructura del borde de la nanocinta y de la energía del electrón. ^[7] ${\displaystyle \lambda _{MFP}\approx 1{\mu }}$

Diamante enriquecido isotópicamente

El diamante isotópicamente puro puede tener una conductividad térmica significativamente mayor. Véase la Lista de conductividades térmicas . ^{[ cita requerida ]}

Véase también

• Circuito adiabático  : circuitos electrónicos de bajo consumo que utilizan lógica reversible para conservar energía.
• Transistor de recolección balística
• Transistor de deflexión balística  : transistor que utiliza fuerzas electromagnéticas en lugar de una puerta lógica.Pages displaying wikidata descriptions as a fallback
• Sobreimpulso de velocidad

Referencias

1. Takayanagi, Kunio; Kondo, Yukihito; Ohnishi, Hideaki (2001). "Nanocables de oro suspendidos: transporte balístico de electrones". JSAP Internacional . 3 (9). S2CID  28636503.
2. Supriyo Datta (1997). Transporte electrónico en sistemas mesoscópicos. Haroon Ahmad, Alec Broers, Michael Pepper. Nueva York: Cambridge University Press. pp. 57–111. ISBN 978-0-521-59943-6.
3. Pastawski, Horacio M. (15 de septiembre de 1991). "Transporte clásico y cuántico a partir de ecuaciones generalizadas de Landauer-Büttiker". Physical Review B . 44 (12): 6329–6339. Bibcode :1991PhRvB..44.6329P. doi :10.1103/PhysRevB.44.6329. PMID  9998497.
4. Pastawski, Horacio M. (15 de agosto de 1992). "Transporte clásico y cuántico a partir de ecuaciones generalizadas de Landauer-Büttiker. II. Tunelización resonante dependiente del tiempo". Physical Review B . 46 (7): 4053–4070. Bibcode :1992PhRvB..46.4053P. doi :10.1103/PhysRevB.46.4053. PMID  10004135.
5. Zhai, C; et al. (2016). "Comportamiento electromecánico interfacial en superficies rugosas" (PDF) . Extreme Mechanics Letters . 9 : 422–429. Bibcode :2016ExML....9..422Z. doi :10.1016/j.eml.2016.03.021. hdl :1959.4/unsworks_60452.
6. Koswatta, Siyuranga O.; Hasan, Sayed; Lundstrom, Mark S.; Anantram, MP; Nikonov, Dmitri E. (10 de julio de 2006). "Balisticidad de transistores de efecto de campo de nanotubos: papel de la energía de fonones y polarización de compuerta". Applied Physics Letters . 89 (2): 023125. arXiv : cond-mat/0511723 . Código Bibliográfico :2006ApPhL..89b3125K. doi :10.1063/1.2218322. ISSN  0003-6951. S2CID  44232115.
7. Koch, Matthias; Ample, Francisco; Joachim, Christian; Grill, Leonhard (14 de octubre de 2012). "Conductancia dependiente del voltaje de una única nanocinta de grafeno". Nature Nanotechnology . 7 (11): 713–717. Bibcode :2012NatNa...7..713K. doi :10.1038/nnano.2012.169. ISSN  1748-3387. PMID  23064554.^{[ enlace muerto permanente ]}

Lectura adicional

• Du, Xu; Skachko, Ivan; Barker, Anthony; Andrei, Eva Y. (2008-07-20). "Aproximación al transporte balístico en grafeno suspendido". Nature Nanotechnology . 3 (8): 491–495. arXiv : 0802.2933 . Bibcode :2008NatNa...3..491D. doi :10.1038/nnano.2008.199. ISSN  1748-3387. PMID  18685637. S2CID  118441080.
• Jalabert, RA; Pichard, J.-L.; Beenakker, CWJ (1994). "Firmas cuánticas universales del caos en el transporte balístico". EPL (Europhysics Letters) . 27 (4): 255. arXiv : cond-mat/9403073 . Bibcode :1994EL.....27..255J. doi :10.1209/0295-5075/27/4/001. ISSN  0295-5075. S2CID  : 55864480.